覆蓋巖溶臨空面對水平承載樁嵌固端承載力的影響試驗研究

李天雨，范秋雁，韓 偉，梁家琿

(1. 山東大學巖土與結構工程研究中心，山東，濟南，250061；2. 廣西大學資源環境與材料學院，廣西，南寧，530004；3. 廣西交投科技有限公司，廣西，南寧，530022)

巖溶發育地區基巖巖性主要是可溶性巖石，在上部滲水和地下水的長期溶蝕作用下，基巖表面會形成溶槽、溶溝等，使得基巖表面起伏落差很大，局部落差較大的位置就會形成基巖陡壁[1]。當樁基礎施工在基巖陡壁邊緣時，加上上部土層的覆蓋，就構成了“覆蓋巖溶臨空面”。“覆蓋巖溶臨空面”是指覆蓋巖溶場地中建筑物基底應力影響范圍內具有陡傾角土巖交界面的一種巖土組合地質體[1?2](如圖1 所示)。當樁受到水平荷載時，覆蓋巖溶臨空面有可能在樁的推力下失穩(特別對于巖體中存在傾斜軟弱結構面的情況)，導致嵌固端失去承載能力。

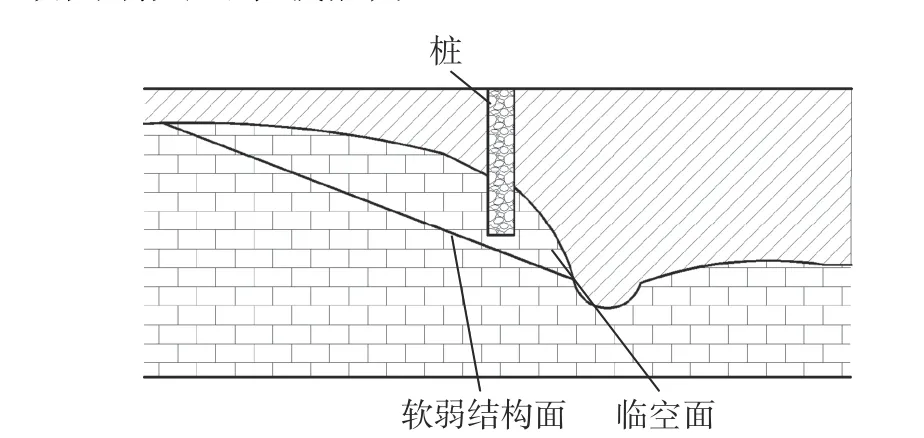
圖1 覆蓋巖溶臨空面(含軟弱結構面)示意圖Fig.1 Schematic diagram of covered karst free surface(including weak structural surface)

對于覆蓋巖溶臨空面的穩定性定量分析方法可分為兩類：第一類是利用經典的梁或板等的力學模型經簡化后求出問題的解析解或近似解析解；第二類是建立較為完整的力學模型采用有限元法等數值方法分析。在第一類研究方法中：黃經秋[3]針對巖體中存在傾斜軟弱結構面的覆蓋巖溶臨空面建立了一個平面剛體力學模型，分析了覆蓋巖溶臨空面的穩定性；李炳行等[4]運用梁板理論分析了兩個工程的巖體臨空面穩定性。在第二類研究方法中：郭密文等[5]對一個具體的工程實例用有限元分析了覆蓋巖溶臨空面的穩定性；范秋雁等[6]和易劍輝[7]建立了一個三維彈性力學分析模型，通過三維有限元計算機模擬建立了一個覆蓋巖溶臨空面存在條件下樁的承載力與多個影響因素之間的定量關系式。Ng[8]對一個具體工程中處于巖溶區石芽尖處的樁基礎穩定性用有限元法進行了分析。以上研究主要針對垂直承載樁條件下，臨空面的穩定性分析，而對于水平承載樁(如抗滑樁、基坑支護樁等)研究較少。本文設計了含臨空面和結構面的樁嵌固段圍巖室內模型，通過水平承載試驗分析了臨空面在樁前和樁后的圍巖破壞形式和破壞機理。在此基礎上，建立了極限狀態下的巖體平衡方程，提出了含臨空面和結構面的嵌固端極限承載力的驗算方法。

1 模型試驗

1.1 相似模型

覆蓋巖溶臨空面的形態(包括臨空面傾角及巖體完整度)，軟弱結構層的厚度、結構面傾角等地質發育情況異常復雜，室內模擬試驗難以全面考慮各種因素的影響，因此本次試驗僅考慮一個軟弱結構面和臨空面的組合情況，設計了臨空面在樁前(模型1)和臨空面在樁后(模型2)兩種模型(如圖2 與圖3 所示)，只研究樁嵌固段巖體的承載能力，不考慮上覆土層對樁的作用。假設樁為連續咬合布置，巖體和樁可視為平面應變模型，且連續咬合樁的剛度遠大于石灰巖圍巖的剛度，故此次試驗將樁體設定為剛性樁，模擬樁體材料采用鋼板焊接的中空箱體，澆筑模型時預留樁體位置，與模擬灰巖材料直接接觸。一般剛性樁入巖深度為樁徑的1.5 倍左右，本文原型設計樁直徑為2 m，故取嵌巖深度為4 m。為減少端部效應，原型樁長設計為10 m(嵌巖段的2.5 倍)，推力加載在出露部分樁體的中間位置。在澆筑時，在結構面設計位置撒一層粒徑為1 mm～2 mm 砂用來模擬軟弱結構層。

圖2 模型1 尺寸及應變花布置圖Fig.2 Model 1 size and strain rosette location

圖3 模型2 尺寸及應變花布置圖Fig.3 Model 2 size and strain rosette location

對于平面問題，平衡方程和變形協調方程如下：

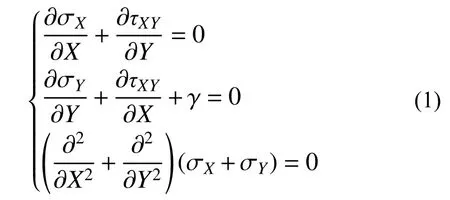
式中： σX、 σY為單元體上的正應力；τXY為單元體上的剪應力； γ為容重。

設應力相似常數為(下標p 代表原型，下標m表示實驗室模型)：

根據相似原理，模型與原型若要相似，式(5)、式(7)和式(6)、式(8)應該相等，可求得相似指標為：

式中：CE為強度相似常數；Cε為應變相似常數，無量綱的物理量，始終為1。

則可推出：

另有：

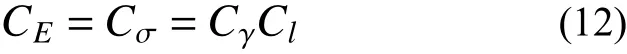
試驗模型采用幾何相似常數為30，物理相似常數為1.3，根據相似判據CE=Cσ=CγCl可得應力或強度相似常數為39。為了較好的模擬灰巖的物理力學性能，本試驗選定了相似材料的原材料為水泥、石膏粉、河砂和重晶石粉，并在攪拌過程中加入硼砂作為緩凝劑[9?10]。試驗中紅黏土通過在原樣紅黏土中參入砂來調節相似材料的強度，達到相似材料強度指標。相關原型巖體和相似模型尺寸和物理力學性質如表1 與表2 所示，表中相似材料抗壓和抗拉強度由巖石無側限單軸抗壓和劈裂試驗測得，內摩擦角粘聚力由快剪試驗測得。

表1 原型巖體與相似模型幾何參數表Table 1 Geometric parameters of prototype rock mass and similar model

表2 原型巖體與相似模型物理力學參數表Table 2 Physical mechanical parameters of prototype rock mass and similar model

1.2 模型架和加載量測系統

模型架由試驗平臺和反力架組成。實驗平臺采用角鋼和鋼化玻璃固定試驗巖體，提供模型理想邊界條件。反力架通過底部的兩條通長槽鋼與試驗平臺焊接在一起，使得該試驗設備能夠在加載方向上保持自平衡。試驗加載設備由分離式千斤頂DYG50-500 及配套電動油泵組成。在千斤頂前端設置荷載傳感器用于測量水平推力，通過電動油泵手輪和截止閥控制加載速度，加載速率為0.2 kN/min。千斤頂的推力施加在樁體出露巖體的中部位置，在樁體同樣的高度對稱布置兩塊百分表1、2，兩塊百分表的平均值作為樁上力作用點位移。在距離樁體左右兩側15 cm、距邊界17.5 cm處分別布置百分表3、4 和百分表5、6，以兩塊百分表的平均值作為樁前和樁后巖體上表面的豎向位移，如圖4 與圖5 所示。在模型前面布置應變花，應變花布置詳圖如圖2 與圖3。

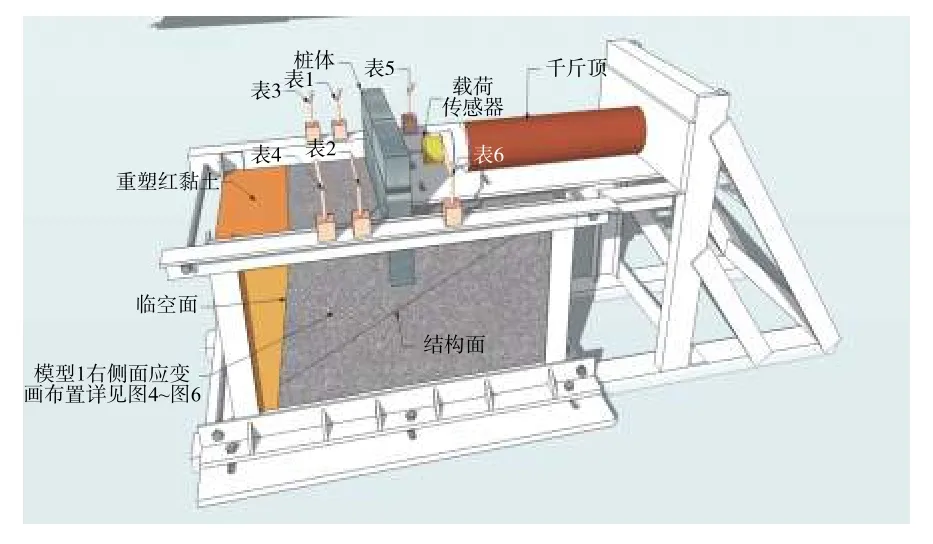
圖4 模型1 設計示意圖Fig.4 Model 1 design diagram

圖5 模型2 設計示意圖Fig.5 Model 2 design diagram

1.3 試驗結果

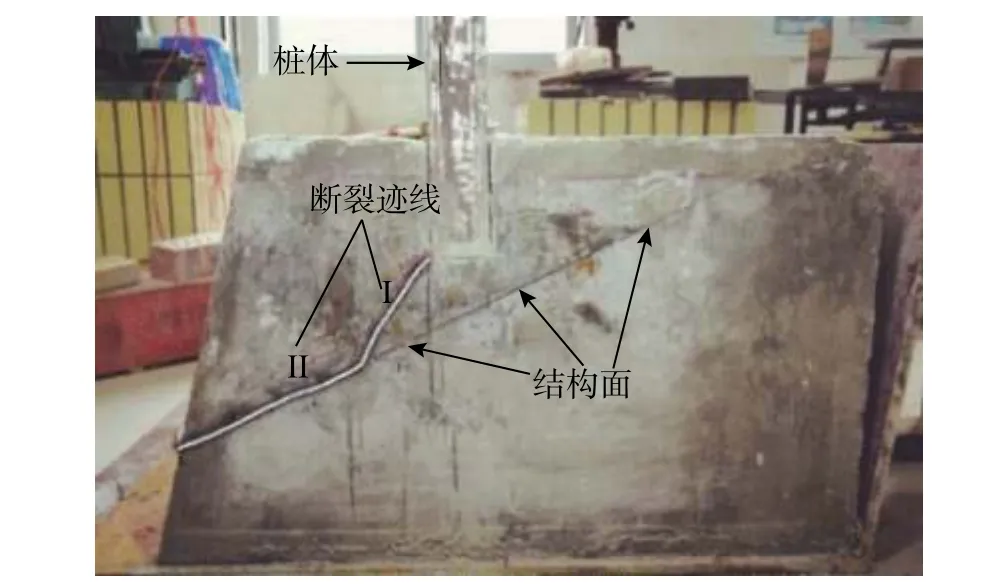
圖6 模型1 斷裂跡線Fig.6 Model 1 fracture trace

圖7 模型1 斷裂跡線Fig.7 Model 1 fracture trace

圖8 模型2 斷裂跡線Fig.8 Model 2 fracture trace

圖9 模型2 斷裂跡線Fig.9 Model 2 fracture trace

模型1 和模型2 的破壞形式一致，都是嵌固端巖體發生脆性破壞，斷裂跡線和斷裂面如圖6～圖9 所示(去除邊界固定并移除紅黏土)。裂紋從靠近臨空面的樁體底角處產生，并快速向結構面擴展，最終和結構面貫通后，在推力作用下將巖體從臨空面推出，導致嵌固端失去承載力。模型1 和模型2 的斷裂跡線都近似為折線形，分為I、II 兩段。I 段為巖石模擬材料內部斷裂，斷裂面凹凸不平，有明顯的受拉破壞現象，其中模型1 的I 段斷裂線與水平面的夾角為53°，模型2 為51°；II 段與結構面重合，表面平整，巖體破壞時沿著結構面滑動，表現為剪切破壞特征。同時，在模型嵌固段其他區域，未觀察到有裂紋開展，模型從加載到破壞沒有明顯的破壞現象發生。由圖10 與圖11 可知，模型1 和模型2 在加載至破壞都可分為3 個階段。彈性變形階段(模型1 為0 kN～3.5 kN，模型2 為0 kN～8 kN)：樁體位移隨著荷載的增加較緩，且巖體豎向位移基本保持不變；非穩定破壞階段(模型1 為3.5 kN～6.5 kN，模型2 為8 kN～11 kN)：樁體水平位移和巖體豎向位移增加速度明顯加快，同時模型內部可聽到偶爾有噼啪聲發出，臨空面一側的巖體有被壓后沿著結構面滑動的趨勢；整體失穩>階段(模型1 為6.5 kN～7.2 kN，模型2 為11 kN～12.34 kN)：模型內部噼啪聲數量及頻率明顯增多，樁體水平位移和巖體豎向位移陡增，巖體突然發生脆性斷裂，巖體沿著結構面向臨空面方向滑移。試驗中過程中，非臨空面側的巖體豎向位移在加載過程中都明顯小于臨空面一側的巖體，此部分巖體保持相對穩定。

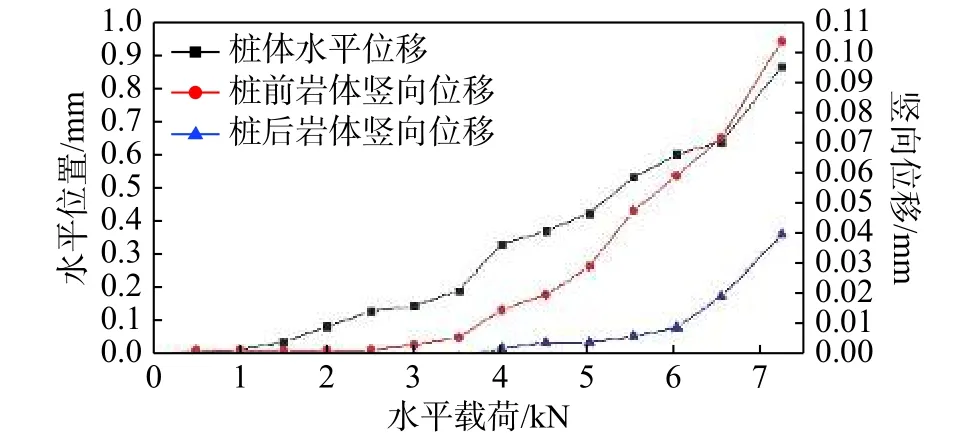
圖10 模型1 水平荷載與各位移關系曲線Fig.10 relation curve between horizontal load and displacement of model 1

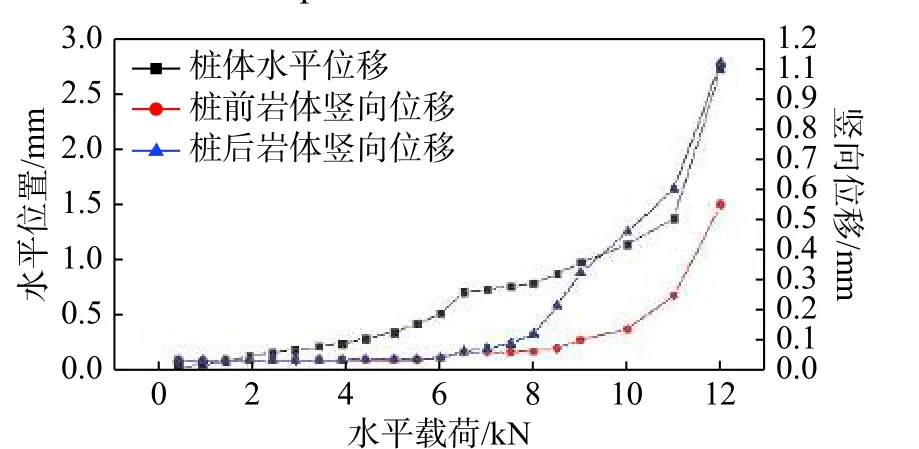
圖11 模型2 水平荷載與各位移關系曲線Fig.11 relation curve between horizontal load and displacement of model 2

模型1 與模型2 結構面以上巖體最大主應變云圖如圖12 與圖13 所示，荷載增加過程中，巖體最大主應變的有明顯正負分界線(拉為正、壓為負)，最大應變為拉應變的區域主要集中在樁底巖體附近。在完整圍巖條件下，通常只在樁后底端附近巖體會產生小范圍最大主應變為拉應變的區域，但由于臨空面和結構面的存在，樁前巖體有向前滑出的趨勢，使樁前巖體底端部分受拉，出現最大主應變為拉應變的情況。隨著荷載的增加，最大拉應變區域逐漸向臨空面一側的結構面延伸，斷裂面都位于樁前拉應變區域內，斷裂面附近最大拉應變逐漸增大，最終形成貫穿的破壞面，表明斷裂面的破壞形式為受拉破壞。非臨空面側的巖體拉應變區域無明顯的擴展現象，此部分巖體在加載過程中保持相對完整。

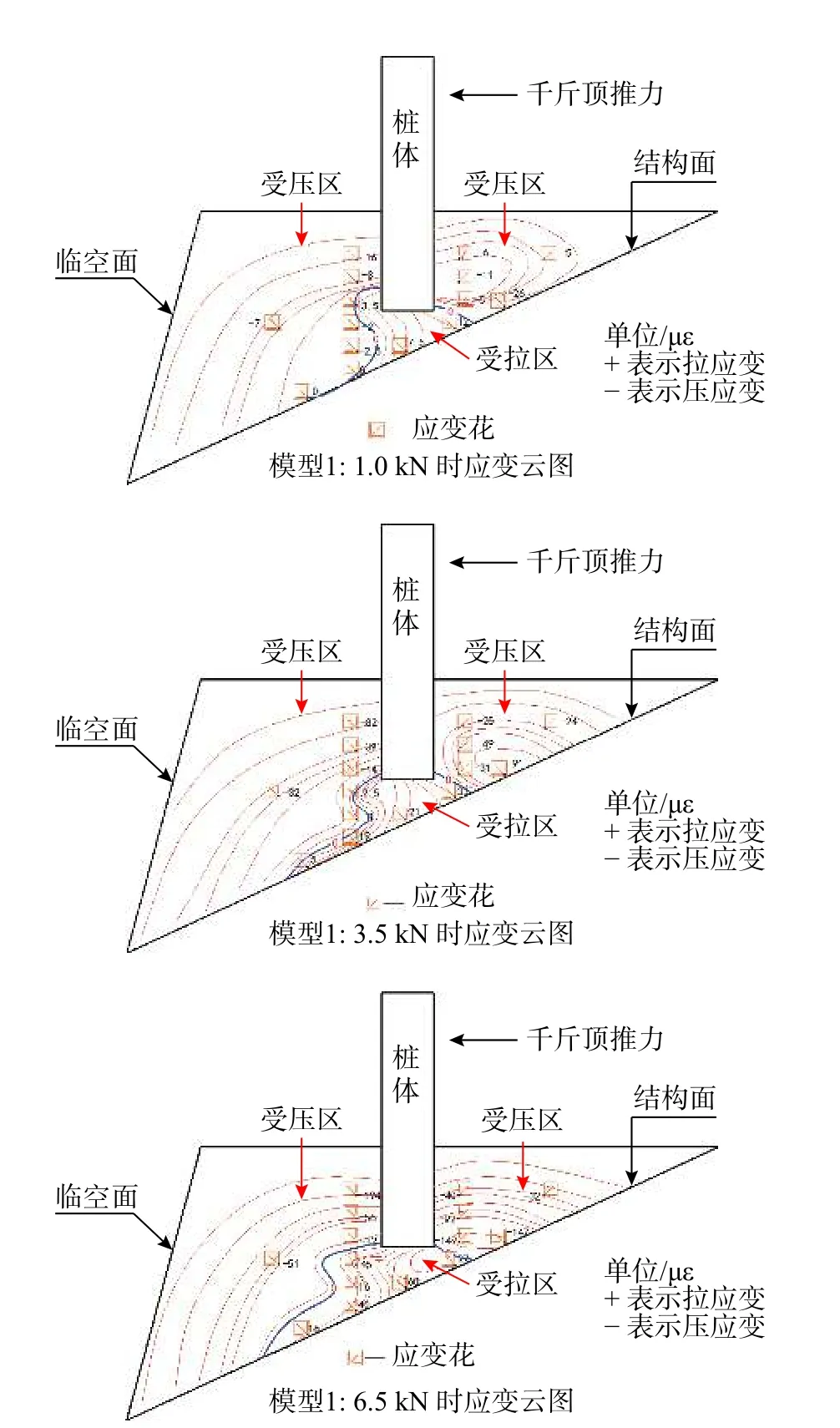
圖12 模型1 各級荷載最大主應變云圖Fig.12 Cloud chart of maximum principal strain of all levels of load in model 1

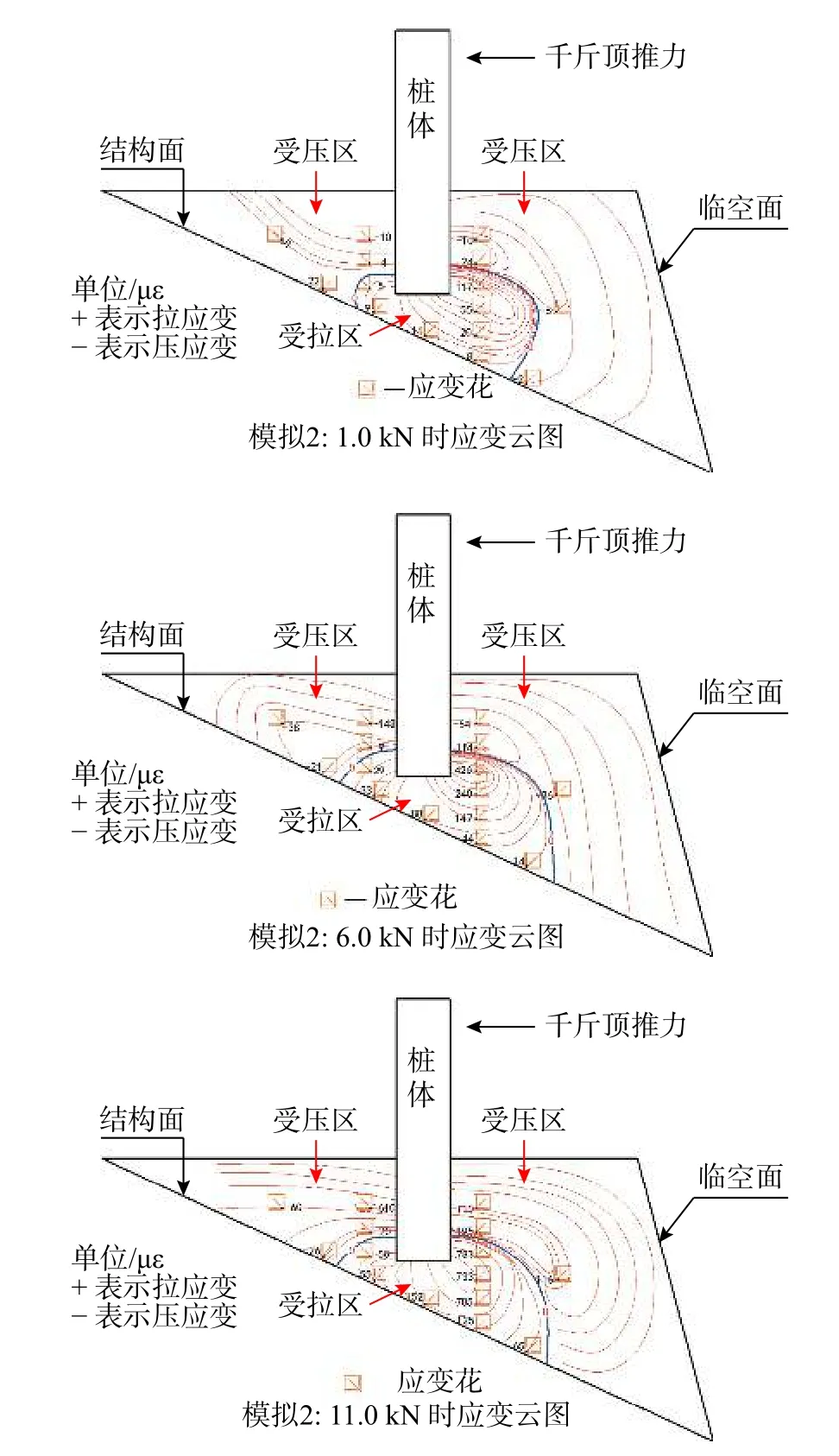
圖13 模型2 各級荷載最大主應變云圖Fig.13 Cloud chart of maximum principal strain of all levels of load in model 2

當嵌固巖體為半無限體條件下時，在推力作用下，巖體破壞形式為樁前巖體產生楔形體塑性區[11]。但模型1 和模型2 都是臨空面一側的巖體整體失穩，樁前巖體尚未進入塑性變形階段，可知臨空面和結構面的存在降低了嵌固端的承載力，同時臨空面位于樁前的水平極限承載力較樁后的更小，樁前臨空面對樁嵌固端承載力的影響更顯著。

2 覆蓋巖溶臨空面和結構面的嵌固段端承載力驗算

2.1 極限狀態下的平衡方程

模型1、模型2 嵌固端破壞形式都是巖體受拉破壞形成斷裂面，斷裂面與結構面交匯后，將巖體從臨空面推出。因此，為了方便計算，做如下假設：斷裂面為平面且垂直于推力和樁所在平面；當嵌固端達到極限承載力時，斷裂面和結構面上的巖體單元都處于極限破壞狀態；斷裂面為受拉破壞，巖體單元達到抗拉強度；結構面為剪切破壞，應用摩爾-庫倫強度準則。按照以上假設，可建立被推出部分巖體(如圖14 所示)的極限平衡方程。

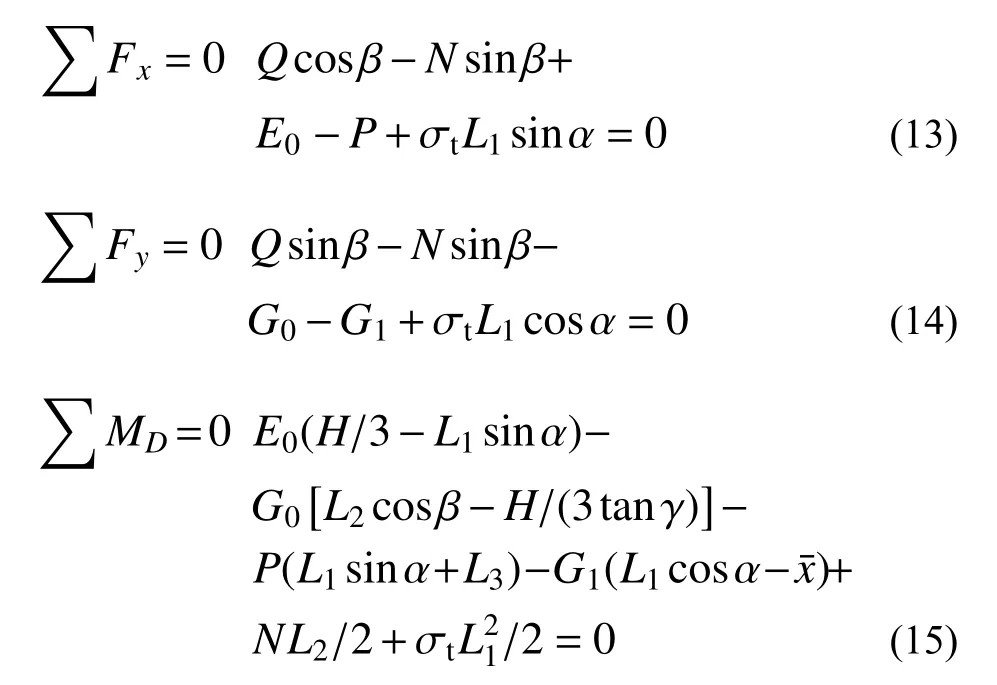
式中：Q為結構面剪力；N為結構面上的法向力；P為樁對巖體的推力，模型1 取樁對樁前巖體的推力，模型2 取樁對樁后巖體的推力；G0為土壓力的豎直分量；E0為土壓力的水平分量；G1為該部分巖體重力；為巖體重心橫坐標； σt為斷裂面的拉應力； α為斷裂面與水平面的夾角； β為結構面與水平面的夾角； γ為臨空面與水平面夾角；L1為斷裂面的的長度；L2為破壞部分結構面的長度；L3為樁對巖推力作用點到樁底的距離。

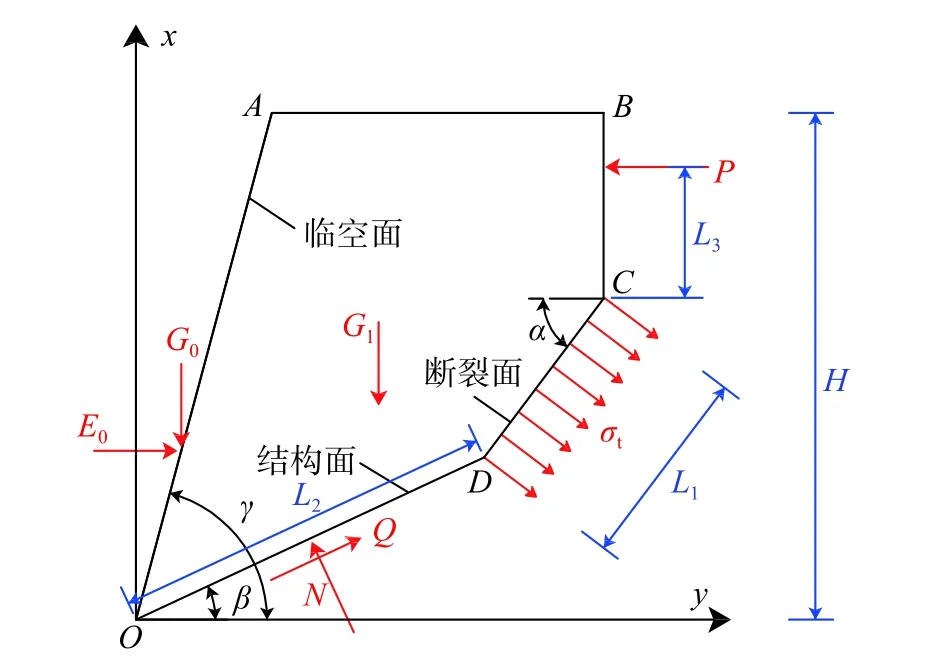
圖14 被推出部分巖體受力示意圖Fig.14 Stress diagram of the pushed part of rock mass

為了驗證以上計算假設和計算方法的可行性，本文根據試驗模擬材料的參數和極限水平荷載，利用式(13)～式(15)反求巖體抗拉強度 σt和斷裂面與水平面的夾角 α，并與試驗結果進行對比。為此方法可用于含覆蓋巖溶臨空面和結構面的嵌固段端承載力的驗算。

2.2 相關參數值計算

結構面達到摩爾-庫倫臨界強度，則剪力Q與法向力N具有以下關系：

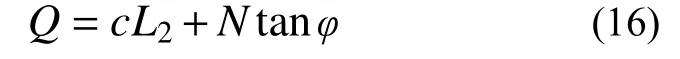
式中：c為粘聚力，對結構面c值為0；φ為結構面內摩擦角。

土壓力采用庫倫被動土壓力計算公式[12]：

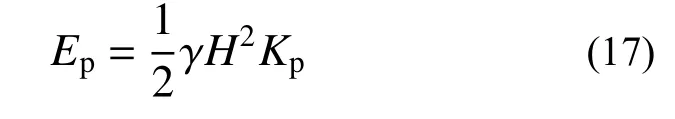
式中：KP為庫倫被動土壓力系數；γ 為土的重度；H為土層高度。

樁對巖體推力P采用剛性樁角位移法進行計算。在推力的作用下，樁將會繞著巖面下處的點x0發生轉動[12](如圖15 與圖16 所示)，則對樁轉動中O點建立平衡方程。

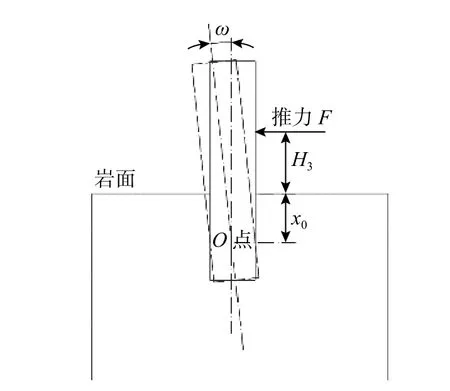
圖15 剛性樁變形示意圖Fig.15 Diagram of rigid pile deformation

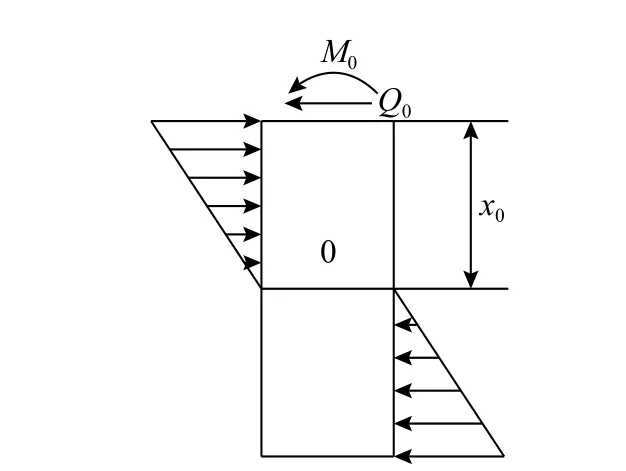
圖16 巖面以下樁受力示意圖Fig.16 Stress diagram of pile under rock surface

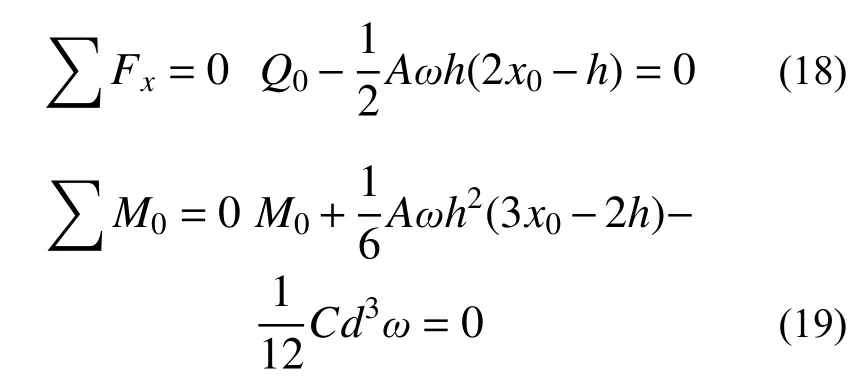
式中：A為巖體側向抗力系數；ω為樁轉動角度；h為嵌巖深度；Q0為將樁上所有外力移至巖體頂面的剪力，本文中千斤頂推力取樁身位移陡增的前一級荷載；M0為滑面以上樁上所有外力對巖體頂面樁中心的力矩；C為巖體豎向地基系數，本文取為A/0.6。

同時，在試驗中已量測了樁體水平位移S，樁體轉動角度較小，樁體水平位移S與ω轉角有以下關系：

式中，H3為推力作用點與巖頂面的距離。

由式(18)～式(20)可推出巖體側向抗力系數A、轉動中心x0及轉動角度ω，則樁側的巖體抗力為[13]：

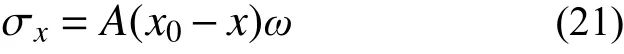
根據相互作用原理，樁對樁前巖體推力P1和樁后巖體推力P2可用下式計算：

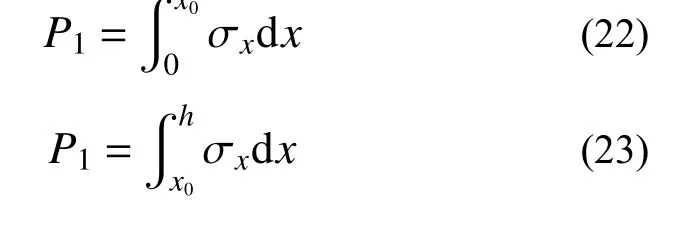
2.3 計算結果

將式(16)、式(17)、式(22)、式(23)計算結果帶入極限平衡方程式(13)～式(15)，可推出斷裂面的極限拉應力 σt和斷裂面與水平面的夾角 α，如表3 所示。在模型1 與模型2 中，斷裂面的極限拉應力 σt和斷裂面與水平面的夾角 α的計算值與試驗實測值均較為接近，誤差都在15%以內，說明以上計算假設和計算方法基本成立。并且計算的拉應力值比試驗實測值更大，在驗算嵌固端承載力時取 σt為巖體的抗拉強度時，更加安全。

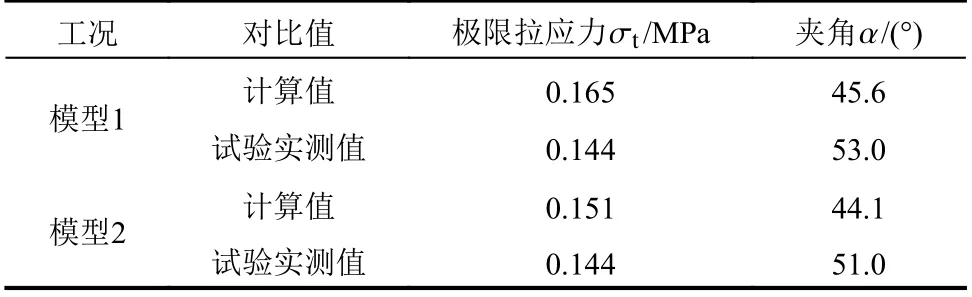
表3 各工況計算結果與試驗實測值對比Table 3 Comparison between calculation results and test measured values of each working condition

對于含臨空面和結構面的嵌固端巖體，在滿足嵌固深度要求后，可采用極限平衡法對嵌固端巖體承載力進行驗算。驗算方法為：在式(13)～式(15)中，令 σt為巖體的抗拉強度，從而求出樁對巖體的推力P，再根據不同剛度條件下分布假設，就可獲得樁嵌固端的極限承載力。由于由(13)～式(15)推出樁對巖體的推力P的數學公式冗長，本文未再列出，實際使用過程種可編制相應求解器對平衡方程進行求解，從而獲得樁嵌固端的極限承載力。本文驗算方法適用于剛性樁，且未考慮上覆土層壓力對巖體的影響。對于柔性樁，需假設柔性的樁端受力分布形式；對于存在上覆土層的情況，需在平衡方程中添加上覆土層壓力。

3 結論

本文設計了包含一個軟弱結構面和臨空面的石灰巖嵌固端室內相似模型，通過室內試驗和假設計算研究了覆蓋巖溶臨空面對水平承載樁嵌固端承載力的影響，得到以下結論：

(1)含覆蓋巖溶臨空面和結構面的嵌固端破壞形式為臨空面一側巖體受拉破壞形成斷裂面，斷裂面與結構面交匯后，沿著結構面方向將巖體從臨空面推出。斷裂面上巖體單元為受拉破壞，結構面為剪切破壞。

(2)臨空面和結構面的存在降低了嵌固端的承載力，同時臨空面位于樁前的水平極限承載力較樁后的更小，樁前臨空面對樁嵌固端承載力的影響更顯著。

(3)建立了巖體的極限平衡方程，并通過比較計算結果和試驗結果，驗證了計算假設條件和計算方法的正確性。當嵌固端巖體存在臨空面和結構面時，在滿足嵌固深度要求后，可采用極限平衡法對嵌固端巖體承載力進行驗算。