大展弦比彈性飛機著陸特性影響因素分析

李新華，陳小榮，史紅偉

(1.北京航空航天大學 航空科學與工程學院， 北京 100191)

(2.中國航天空氣動力技術研究院 彩虹無人機科技有限公司， 北京 100074)

0 引 言

根據飛機的低階固有振動頻率，一般將飛機機體低階固有頻率介于0.5～2.0 Hz之間的視為彈性飛機[1-2]。傳統方法對于飛機著陸特性的分析，多數采用二質量模型對機體和起落架系統進行分析[3]，并將機體視為剛性體。隨著飛機結構制造技術的發展，飛機的展弦比越來越大，特別是復合材料的大量采用，飛機機體的低階固有頻率越來越低，機體的彈性越來越大，甚至部分飛機機體變為柔性，從而對著陸特性帶來越來越明顯的影響[4-5]。

國外，A.E.McPherson等[6]考慮機翼柔性的影響，用自由梁模型模擬機翼，剛性質量塊模擬機身，研究柔性機翼對起落架緩沖性能的影響；F.E.Cook等[7-8]考慮了柔性機翼的剛體模態和振動模態，建立了多質量塊等效模型，研究結果表明柔性機翼可以有效減緩著陸載荷；M.Spieck等[9]基于多體動力學建立飛機著陸動力學模型，進行了著陸動力學仿真。

國內，史友進等[10-11]、劉錦陽等[12]、廖麗涓等[13]基于多質量塊模型，建立著陸動力學模型，對著陸性能進行了分析；史紅偉等[14]基于拉格朗日方法對剛性體、彈性體以及帶阻尼彈性體大展弦比飛機著陸特性進行了對比分析，其結果表明彈性效應可以有效減緩著陸沖擊響應，阻尼系數對著陸能量耗散有積極作用。已有的研究工作表明彈性模態、柔性機翼等對著陸影響等有積極影響，但是缺少對飛行器設計的具體指導和反饋。

本文采用拉格朗日方法，對帶阻尼彈性體飛機著陸沖擊響應進行仿真分析，分析彈性模態質量、起落架安裝點廣義位移、彈性振動頻率和結構阻尼系數對飛機著陸沖擊響應和著陸能量耗散的影響。

1 動力學模型

本文采用模態疊加的方法，以大展弦比彈性飛機和常規支柱式油氣緩沖式起落架為研究對象，建立起落架系統和彈性機體的振動模態數學模型。

以大展弦比彈性飛機機體為例，根據拉格朗日方程，建立考慮結構阻尼的彈性機體n階模態動力學方程。

大展弦比彈性飛機低階對稱運動模態主要是機翼的彎曲和扭轉變形，分析中取飛機右側一半的對稱模型(如圖1所示)，建立地面固定坐標系Oxyz，原點位于輪胎著陸地瞬間機體的質心位置，x軸指向航向位置，y軸垂直于機體對稱平面沿展向布置，z軸鉛垂向下。

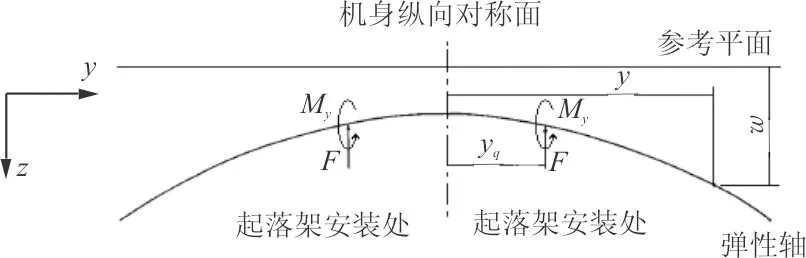
(a) 機身展向沿彈性軸的坐標

考慮結構阻尼的彈性機體n階模態動力學方程為

(1)

以支柱式油氣緩沖起落架為研究對象，建立地面固定坐標系Oxyz，原點位于輪胎接地瞬間的中心位置，各坐標軸分別與機體地面坐標系平行，運動微分方程為

(2)

式中：Fz為緩沖器軸向力，其可簡化為油液阻尼力Fzs和空氣壓力Fza兩者之和，油液阻尼力為

(3)

式中：Cs為油液速率平方阻尼；s為緩沖器行程。

空氣壓力表示為

(4)

式中：Pa0為空氣腔初始壓強；Aa為空氣腔有效壓氣面積；Va0為空氣腔初始容積；γ為空氣腔壓縮多變指數，一般取1.1～1.4。

Fv為輪胎支反力，有

(5)

式中：CT為輪胎垂直振動阻尼系數，一般取0.04；mTδT為輪胎靜壓曲線函數，可由輪胎試驗確定；δ為輪胎壓縮量，其中：

(6)

綜合彈性飛機機體動力學模型和起落架運動模型，計算大展弦比彈性飛機著陸一階運動微分方程。

異步階段，緩沖器壓縮，同步階段的末值作為此階段的初始值，得到：

上述的彈性飛機著陸動力學模型采取了下列假設：

(1) 飛機的結構變形采用準模態法，飛機運動采用線性振動理論描述；

(2) 飛機對稱運動，只保持垂直運動方向的自由度，且飛機接地瞬間時刻為零點；

(3) 主起落架與機體之間垂直安裝；

(4) 不考慮機翼彈性形變導致的飛機升力變化；

(5) 不考慮扭轉模態的影響。

2 仿真結果與分析

以全球鷹無人機為例，通過動力學仿真，計算分析彈性飛機模態質量、廣義安裝位置、低階固有頻率和結構阻尼等因素對飛機著陸沖擊特性的影響，全球鷹無人機的狀態參數如表1所示，并以此參數為分析比較的基準。

表1 全球鷹無人機狀態參數

2.1 彈性模態質量影響對比

改變飛機彈性模態質量，研究模態質量500、1 000、1 500 kg對彈性飛機著陸時緩沖器載荷、緩沖器行程、緩沖器速度以及輪胎支反力的影響。

彈性機體各模態質量下緩沖器載荷、行程、速度、輪胎支反力隨時間變化曲線分別如圖2～圖5所示，可以看出：隨著彈性模態質量的提高，緩沖器載荷、緩沖器行程和輪胎支反力的峰值也隨之提高，但變化量不大，約為10%。彈性模態質量1 000和1 500 kg時的峰值相差不大，表示在此模態質量下緩沖器已壓縮至最大值。飛機設計時需要考慮彈性模態質量與緩沖器行程之間的聯系，避免緩沖器達到最大行程。緩沖器載荷、行程、速度、輪胎支反力隨時間的衰減基本相同，表明彈性模態質量對沖擊的能量耗散沒有影響。

圖2 模態質量對緩沖器載荷影響

圖3 模態質量對緩沖器行程影響

圖4 模態質量對緩沖器速度影響

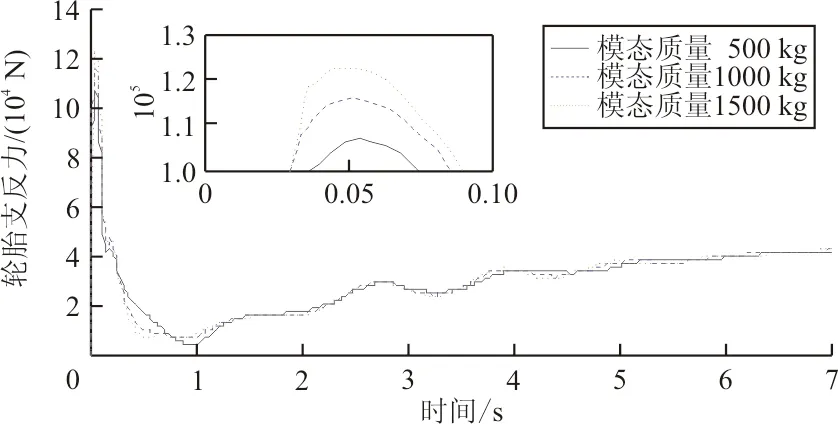
圖5 模態質量對輪胎支反力影響

從能量轉換的角度來看，飛機通過著陸沖擊，將沖擊時垂直方向動能的一部分轉換為機體的彈性勢能，另一部分則通過緩沖器進行耗散；彈性模態質量影響初始動能轉化為機體彈性勢能的量，由此造成模態質量增強，緩沖器沖擊載荷也加強。

2.2 安裝點廣義位移影響對比

起落架安裝點廣義位移ξ1實際上是指起落架安裝位置處的模態函數，其與彈性模態質量一起影響二質量模型的質量比。當取值為0時，飛機運動表現為只有剛體模態下的特性，即為剛體模態，取值越大，彈性效應越明顯。改變安裝點廣義位移，研究安裝點廣義位移0.1、0.2、0.3對彈性飛機著陸時對緩沖器載荷、緩沖器行程、緩沖器速度和輪胎支反力的影響。

各安裝點廣義位移彈性狀態下緩沖器載荷、行程、速度、輪胎支反力隨時間變化曲線分別如圖6～圖9所示，可以看出：隨著安裝點廣義位移變大，緩沖器載荷、行程、速度、輪胎支反力四個變量的峰值逐漸減小，且衰減速度變快。由于安裝點廣義位移越大，彈性效應越明顯，表明安裝點廣義位移，即彈性效應，既可以顯著降低飛機的著陸沖擊載荷，又可以加快著陸沖擊能量的耗散，使飛機著陸過程更加平穩，對于改善飛機的著陸品質具有重大意義。

圖6 安裝點廣義位移對緩沖器載荷影響

圖7 安裝點廣義位移對緩沖器行程影響

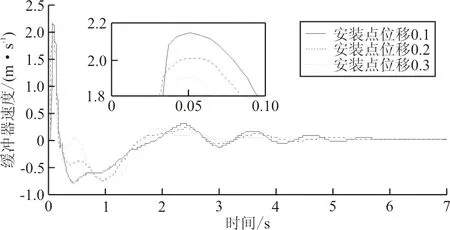
圖8 安裝點廣義位移對緩沖器速度影響

圖9 安裝點廣義位移對輪胎支反力影響

2.3 機體結構阻尼系數影響對比

改變機體結構阻尼系數，考慮機體結構阻尼系數0.1、0.2、0.3對彈性體飛機著陸時緩沖器載荷、緩沖器行程、緩沖器速度和輪胎支反力的影響。

各阻尼系數彈性狀態下緩沖器載荷、行程、速度、輪胎支反力隨時間變化曲線分別如圖10～圖13所示，可以看出：各阻尼系數下，緩沖器載荷、行程、速度和輪胎支反力的最大峰值相差不大，但是在各條曲線峰值之后的振蕩衰減中，阻尼系數較大時，震蕩比較平緩。

圖10 阻尼系數對緩沖器載荷影響

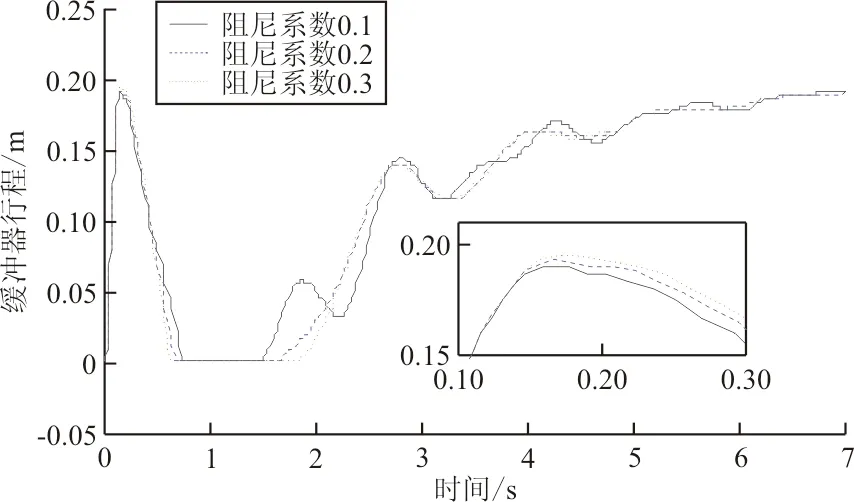
圖11 阻尼系數對緩沖器行程影響

圖12 阻尼系數對緩沖器速度影響

圖13 阻尼系數對輪胎支反力影響

從能量轉換的角度來看，著陸時垂直方向動能分別分配給機體和著陸緩沖器，機體通過彈性形變將能量緩存起來，在沒有結構阻尼的情況下，會逐步釋放給著陸緩沖器進行耗散；在有結構阻尼的情況下，緩存的勢能一部分會釋放給著陸緩沖器，一部分通過結構阻尼進行耗散，結構阻尼越大，釋放給著陸緩沖器的能量越少，著陸越平緩，表現為著陸緩沖器載荷、行程、速度等曲線變化較為平緩，因此結構阻尼是改善飛機著陸品質的重要參數。

2.4 彈性振動頻率影響對比

改變機體彈性振動頻率，研究彈性振動頻率對著陸時緩沖器載荷、行程、速度和輪胎支反力的影響。需要注意的是，根據彈性飛機低階固有頻率要求，取值要介于0.5～2.5 Hz間，且盡量貼合模型原有參數，因此，分別選取頻率分別為0.84、1.04和1.24 Hz。

各振動頻率彈性狀態下緩沖器載荷、行程、速度、輪胎支反力隨時間變化曲線分別如圖14～圖17所示，可以看出：各彈性振動頻率下，緩沖器載荷、行程、速度和輪胎支反力的最大峰值相差不大；各變化曲線的波動頻率變化與振動頻率變化一致，振動頻率越低，曲線波動頻率也越低，且具有更快的衰減速率。

圖14 彈性振動頻率對緩沖器載荷影響

圖15 彈性振動頻率對緩沖器行程影響

圖16 彈性振動頻率對緩沖器速度影響

圖17 彈性振動頻率對輪胎支反力影響

從能量轉換的角度來看，飛機彈性振動頻率不會改變著陸沖擊垂直方向動能轉換的能量分配，因此各曲線峰值相差不大；但是振動頻率會影響轉化為機體彈性勢能的能量通過結構阻尼進行耗散的效率，彈性較大(振動頻率低)具有較高的耗散效率，導致彈性勢能儲存的能量釋放給緩沖器的能量減少，各參數衰減速度加快，飛機著陸品質改善。

3 結 論

(1) 彈性模態質量和安裝點廣義位移能夠影響飛機緩沖器載荷、行程、速度以及輪胎支反力。模態質量越小，安裝點廣義位移越大，緩沖器載荷等越小，反映在飛機設計過程中這兩個參數能夠顯著影響起落架設計要求。

(2) 安裝點廣義位移、結構阻尼系數和機體彈性振動頻率能夠影響著陸沖擊能量耗散效率。安裝點廣義位移越大，結構阻尼系數越大，彈性振動頻率越小，著陸沖擊耗散速率越快，飛機著陸越平穩。