飛翼無人機機動飛行非線性反步控制律設計

楊雷恒，李繼廣，楊璐，岳源

(1.西安航空職業技術學院 通用航空學院， 西安 710089)

(2.西安航空學院 通用航空工程技術中心， 西安 710077)

(3.中國民用航空飛行學院 航空工程學院， 廣漢 618307)

0 引 言

飛翼無人機由于具有良好的隱身性能、較大的升阻比等優點受到了各國的普遍重視，得到了較快的發展。雖然飛翼布局的優勢突出，但其特殊的構型也為控制律設計帶來了一系列的困難：

(1) 垂尾的缺失使得航向穩定性弱，且存在更大的耦合和非線性特性[1-2]；

(2) 控制效率低下使得機動飛行時非線性、遲滯效應、不確定擾動等的影響更加突出[3-4]；

(3) 機動飛行的飛行狀態快速改變使得經典控制理論所要求的平衡點并不存在，這也使得經典控制方法失去了理論基礎[5-6]。

針對飛翼無人機機動飛行面臨的實際問題，各國研究者提出了不同的解決方法。L.Sonneveldt等[6]、S.Sieberling等[7]、W.MacKunis等[8]從不同的理論角度出發研究了無人機的非線性控制問題。這些研究結果對解決飛翼無人機機動飛行控制律設計是有利的，但是這些方法也存在著設計過程復雜、對系統模型精確高度依賴、魯棒性無法保證等缺點。為了解決系統魯棒性能設計問題，E.N.Johnson等[9]、Xu Bin等[10]做了專門的研究設計，并在X-35和F-18的模型機上進行了仿真驗證。這些方法雖然提高了系統的魯棒性，但是設計過程要求系統不確定性是有界且已知的。

目前，已經發展了很多非線性控制律設計方法。在眾多非線性控制方法中，反步(Backstepping)控制方法因其具有處理非線性系統控制的能力，在飛翼無人機控制系統設計上表現出明顯的優勢并得到了廣泛的重視。然而，傳統Backstepping方法同樣具有魯棒性弱、設計過程復雜等不足。為了提高系統的魯棒性，研究者提出了改進方法[11-12]。但是，這些方法在提高系統魯棒性的同時，也帶來了奇異值計算、保守性等問題。

本文針對奇異值計算、保守性問題，提出一種改進的Backstepping方法，運用該方法進行控制器設計，并對控制器進行仿真驗證。

1 系統建模

被控飛翼無人機示意圖如圖1所示，可以看出：該無人機是典型的飛翼布局，控制舵面主要包括升降副翼，兩邊舵面聯動相當于升降舵，兩邊舵面差動相當于副翼；同時，該無人機具有阻力式方向舵。

圖1 無人機示意圖

為了表述方便，將無人機的姿態方程表述為如下形式：

(1)

式中：ω=[p,q,r]T；MA為無人機運動與空氣的相互作用而產生的氣動力矩；MT為發動機矢量噴口偏轉而產生的矢量力矩；I和S(ω)分別為慣性矩陣和ω的反對稱矩陣。

發動機的矢量力矩，一般用發動機的油門開度δth、發動機噴口矢量角縱向偏轉角度δp和橫向偏轉角度δy進行調節。當發動機推力作用點到質心沿機體軸的距離為xT,推力大小表示為飛行狀態和油門開度的狀態函數T(x,δth)時，則發動機的矢量力矩為

(2)

無人機的姿態角運動方程為

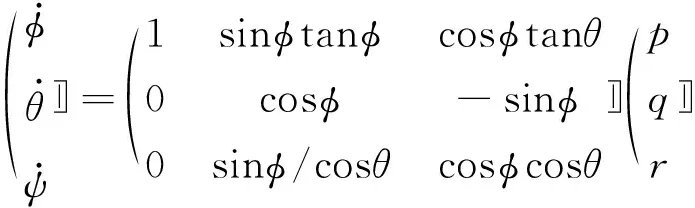
(3)

式(1)所確定的飛翼無人機姿態方程和由式(3)確定的內環補償控制律所組成的系統，可以表示成如下仿射非線性模型的形式：

(4)

(5)

式中：x1=[φθψ]；x2=[pqr]。

式(4)～式(5)的具體表達形式參見參考文獻[2-3]。

為保證控制器的魯棒性，將模型表示為包含有不確定性的攝動模型：

f1(x1)=f10(x1)+Δf1(x1)

(6)

b1(x1,x2)=b10(x1,x2)+Δb1(x1,x2)

(7)

b2=b20+Δb2

(8)

f2(x1,x2)=f20(x1,x2)+Δf2(x1,x2)

(9)

式中：f10(x1)、b10(x1,x2)、f20(x1,x2)、b20為系統的標稱參數，其余為系統的不確定項。

2 魯棒控制器設計

2.1 姿態角控制器設計

魯棒自適應控制器設計的目的是在各種不確定性有界擾動的情況下，使得飛翼無人機系統的飛行狀態收斂到任一指定無窮小的鄰域內。令系統的誤差量z1,z2∈R3為

(10)

式中：x1d,x2d為期望的系統狀態軌跡。

由式(4)～式(5)可得誤差狀態的動態方程為

(11)

(12)

對于式(7)所確定的系統，其攝動模型可以表示為

Δb1(x1,x2)x2

(13)

令： Δ1=Δf1(x1)+Δb1(x1,x2)x2,

則：

(14)

式中：Δ1是系統的不確定項，即需要引入不確定函數進行補償的各種不確定因素。

就實際系統而言，其不確定性是有界的，則存在一未知的正實數ρ1使得下式成立：

‖Δ1‖≤ρ1δ1(x1,x2)

(15)

式中：δ1(x1,x2)為已知的非負光滑函數。

將x2作為式(12)系統的虛擬控制量，則存在一個理想的虛擬控制量：

(16)

選取虛擬控制量為

(17)

式中：η1為需要設計的魯棒函數系數，其作用是抵消各種不確定性因素Δ1的影響。

(18)

對式(18)求導可得：

(19)

根據文獻[12-13],選擇自適應調解律：

(20)

魯棒函數系數η1和函數l1為

(21)

式中：ε1>0是需要的設計參數。

因為：

所以：

(22)

根據Lyapunov穩定性定理可知，該系統是穩定的。

2.2 角速率控制器設計與穩定性分析

由文獻[12,13]可知，飛翼無人機姿態角控制器存在一個理想的控制輸入：

(23)

使得式(24)成立。

(24)

式中：k2,k為要設計的大于零的參數。

(25)

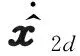
對于研究對象來說，存在一個未知的正實數ρ2，使得:

‖Δ2‖≤ρ2δ2(x1,x2)

(26)

式中：δ2(x1,x2)為已知的非負光滑函數。

選取控制量：

(27)

式中：η2為期望提高系統魯棒性而引入的魯棒控制函數。

將式(27)帶入式(24)可得：

b2(η2-Δ2)

(28)

選取Lyapunov函數：

(29)

對式(29)求導可得：

(30)

選擇魯棒函數和自適應調解律為

(31)

式中：

因此，系統是穩定的。

通過以上證明過程，有以下定理。

定理：對于由式(4)和式(5)所確定的系統，采用式(16)和式(27)所確定的虛擬控制量和控制量、以及自適應參數調解律，則系統的跟蹤誤差z1、z2參數估計誤差有界，且以指數形式收斂于系統原點的一個鄰域：

(32)

從以上定理可知，對于由式(4)和式(5)所確定的系統，通過調節k1、k2、σ1、σ2、r1、r2的值可以調節系統的收斂速度和收斂域。

3 仿真驗證

表1 偏移幅度表

為了更好地對比說明，本文采用動態逆設計方法和傳統Backstepping方法進行仿真對比。其中，文獻[7]提出的增量動態逆魯棒設計方法(簡稱方法1)和文獻[11]提出的一種滑模控制技術和Backstepping控制技術結合的無人機魯棒非線性控制器(簡稱方法2)作為本文仿真的對照組。

滾轉角通道響應如圖2所示，曲線誤差如圖3所示，可以看出：三種方法具有不同程度的超調和穩態誤差，但本文方法超調量更小，且沒有穩態誤差。但是，在方波信號的下降段，本文方法出現比較大的尖峰誤差。

圖2 滾轉角通道方波響應

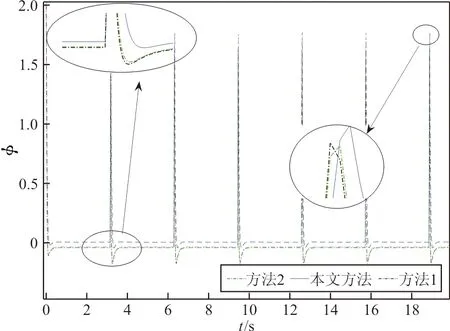
圖3 滾轉角通道方波響應誤差

迎角通道正弦響應如圖4所示，可以看出：本文提出方法具有更小的跟蹤誤差，而對照組方法具有相似的控制效果。

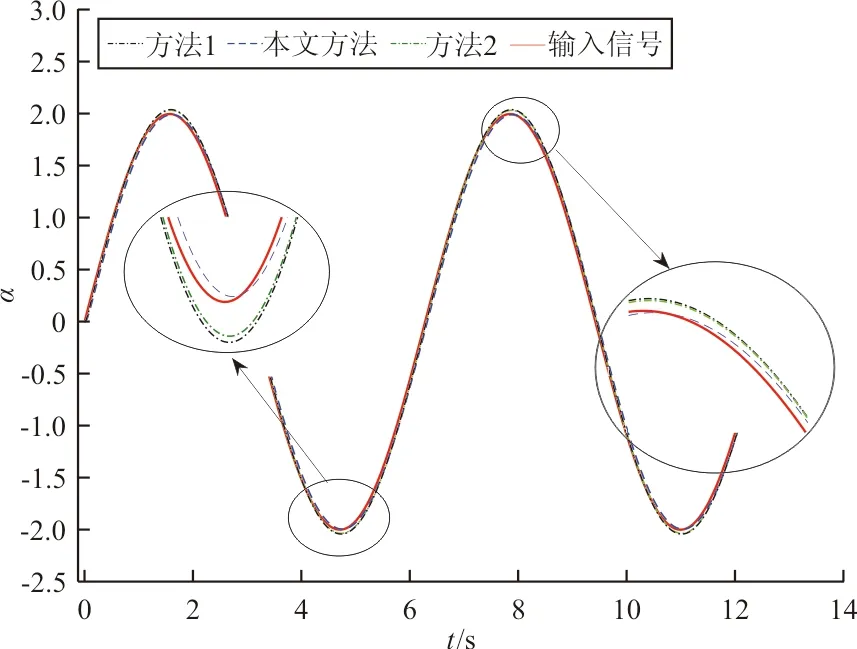
圖4 迎角通道正弦響應

綜上所述，本文方法在方波響應上升段和下降段的響應速度不如方法1和方法2，這也是圖3中出現較大尖峰誤差的原因。綜合來看，本文所提出的設計方法具有較大的優勢。

4 結 論

(1) 本文提出的改進Backstepping方法突破了現有非線性魯棒設計方法對系統不確定性范數上界已知要求的限制，并充分利用系統已知的信息提高系統的性能。

(2) 該方法解決了魯棒自適應函數設計過程中的奇異值計算問題和系統的保守性問題，具有較強的魯棒性，和現有的方法相比具有一定的優勢。