航天器再入隕落解體模型及分析預報策略研究

唐小偉，李四新，石衛波，黨雷寧，李志輝

(中國空氣動力研究與發展中心超高速空氣動力研究所， 綿陽621000)

1 引言

隨著人類在大氣層外航天活動的逐漸增多，航天器離軌隕落再入問題逐漸受到關注和重視。這類問題屬于典型的非常規再入問題[1-2]。 所謂非常規再入問題即指各種人造飛行物如失效衛星、軌道艙、空間站、重復使用航天器(故障情況)、多級運載火箭等在無控飛行或受控變軌后軌道衰降并再入地球大氣層的過程。 這些再入隕落的航天器往往不是用于在大氣層中飛行的，或者處于非設計飛行狀態，沒有專門的氣動布局外形及熱防護措施。 航天器超高速飛行進入大氣層后，在強烈氣動力/熱作用下，其原始構型整器會出現解體，金屬材料軟化熔融，復合材料熱解/燒蝕以及期間或伴隨燃燒或爆炸等劇烈反應現象。對航天器再入隕落解體過程的把握和定性理解是進行建模及分析預報的前提。

國外關于航天器再入隕落解體分析預測及地面風險評估的研究已有20 余年，建立了相對成熟的軟件系統[3-5]，比如美國NASA 的DAS 和ORSAT[6-8]等，歐空局(ESA)的DRAMMA、SESAM 和SCARAB 等[9-11]。 國內開發的有隕落預測軟件如DRAPS，受眾小、應用力度不夠[12-14]。

面向物體法和面向航天器法是由德國學者Lips 和Fritsche 提出的關于航天器再入隕落分析的分類方法[3]。 面向物體法的基本思路是將復雜航天器結構簡化為簡單形狀物體，比如圓球、圓柱、箱體等，建模簡單并且計算速度快，適宜于大量碎片再入的快速預測，DAS 和ORSAT 均屬于這一類方法。 面向航天器法則盡可能模擬真實的航天器外形，采用基于表面網格的飛行器和碎片模型，理論上講具有更高的預測精度，但建模較復雜并需要較長的計算時間，SCARAB 是目前唯一屬于面向航天器法的軟件。

唐小偉等[15-16]開展了再入隕落相關工程實例的應用分析，包括對多級運載火箭發動機殘骸高速墜入大氣層、失效小衛星隕落再入損毀情況及某衛星使用的放射性同位素熱源組件再入進行了計算分析。 基于彈道-氣動力-氣動熱的綜合計算分析的技術途徑，針對LTG(類似天舟、天宮等)軌道艙再入隕落解體過程進行了分析預報。經驗表明，航天器再入隕落解體過程中各種現象具有很大隨機性，從解決工程問題的角度，復雜的航天器精細建模不一定能夠反映系統的不確定性。 航天器再入隕落解體過程的分析預報，從技術途徑概述就是要得出氣動力/熱和航天器物理(解體/運動)化學(熱解/燒蝕)狀態交互作用的過程。 從技術邏輯分析，航天器解體及其導致的物形變化是氣動力/熱分析的基礎；對航天器及其解體后對象氣動力/熱的準確分析，是研究對象飛行運動、殘骸存活性、殘骸落區及地面風險評估的關鍵。

為此，本文首先針對航天器再入隕落解體分析預報的研究對象，綜合以往工作經驗歸納提煉出一種新型簡潔的航天器再入隕落解體模型——三層級模型；然后針對航天器再入隕落解體分析預報的技術途徑，提出基于條件邊界的參數統計方法；最后通過相關軟件研制和一例大型航天器再入隕落解體過程分析預報表明文章提出的模型和方法的適用性。

2 再入隕落解體過程技術簡析

如前所述，航天器再入隕落解體過程分析是典型的非常規再入問題[1-2]，這類航天器再入過程中的主要技術問題包括飛行運動、氣動力、氣動熱和結構解體4 個方面。

對航天器再入隕落過程進行分析時，對飛行運動的把握是貫穿全過程的主要線索，也是分析預報建模關注的主要內容之一。 在航天器整器解體前，對其進行精確的氣動力/熱及運動分析具有重大意義，有助于對整器解體時刻的飛行高度、速度等參數進行準確推斷；由于隕落解體后的航天器部件或碎片外形一般都比較復雜，質量特性及外形仍然處于持續變化之中，導致飛行運動姿態及相關的氣動力/熱作用存在極大不確定性。 對于此類問題，要獲得隕落體部件或碎片的姿態變化歷程是困難的，且不具備充分的工程意義。

氣動力問題是隕落體再入/進入大氣層時面臨的最重要和最復雜的技術問題之一。 力是運動變化的直接原因；隕落體受到的重力相對較為確定，因而氣動力的準確分析是隕落體運動動力學評估的基礎。 隕落體再入飛行過程中，穿越了自由分子流區域(高度100～120 km 以上高空)及過渡流區域(約高度70～120 km 區間)，其部分殘骸碎片可能會穿過連續流區域(約高度70 km 以下)直至地球表面。 隕落體飛行過程中涉及到氣動力分析，以及跨流域、復雜外形、氣動物理等方面的多種手段。 對這些氣動力相關科學問題的探索，可牽引發展以求解Boltzmann 方程可計算建模為核心的跨流域氣體動理論統一算法基礎研究、稀薄氣體動力學DSMC 數值模擬研究、過渡流區域N-S/DSMC 耦合算法研究及考慮熱化學非平衡效應的近連續流區、連續流區N-S 方程數值模擬研究。

隕落體飛行穿越大氣層過程中，高超聲速運動必然會帶來強烈的氣動熱作用。 氣動熱分析主要反饋其對隕落體的外形影響及物性變化，作為解體分析判斷的依據，并作為氣動力分析的重要基礎。 氣動熱問題可細分為熱環境、金屬材料軟化/熔融和復合材料熱解/燒蝕3 個方面，劇烈的爆炸或燃燒反應也和氣動熱作用密切相關。

熱環境分析的主要目標是獲得隕落體表面的對流換熱情況，這是后續材料結構破壞及解體分析的基礎。 隕落體主要是一些壽命末期的大型軌道飛行器、人造衛星或上面級運載火箭分離拋棄的殘骸等，它們絕大部分由金屬或合金材料(統稱為金屬材料)構成。 因此，對金屬材料軟化/熔融導致的破壞情況進行分析評估是非常重要的方面。 在高速氣流氣動加熱作用下，金屬材料構件會逐漸升溫；當溫度上升到一定程度，金屬材料會出現軟化現象；當溫度達到熔點，金屬材料將發生熔融。 航天器再入隕落飛行過程中，對金屬材料軟化/熔融的分析目的在于獲得其由于軟化或熔融而導致的結構破壞和解體情況。 雖然再入大氣層內的人工天體類隕落體一般絕大部分由金屬材料構成，但是仍然有部分部件是由復合材料構成的，主要是一些氣瓶、貯箱之類。 復合材料在氣動熱作用下一般要經歷升溫、熱解和燒蝕等復雜的物理化學過程，這是航天器再入隕落分析預報中需要重點關注的技術問題。

進入大氣層內的隕落體可能呈現出的最明顯表象即是結構失效崩潰及激烈的解體。 結構解體形成的部件或碎片形狀是氣動力、氣動熱評估分析的幾何基礎，解體后部件或碎片的質量特性及運動參數同時也是后續彈道預測的主要依據。 如果要剖析結構解體的細節，須基于固體力學為基礎的嚴格的內應力分析，融合氣動力/熱對結構產生的物理化學作用，并考慮其它影響因素(如重力、自旋等)的作用。 原則上，結構解體屬于典型的固體力學問題，屬于固體力學中材料的應變應力分析技術問題。 通過數值模擬方法可獲得每一處結構微元體的應變、應力，結合材料當地條件下的物性參數和破壞判據給出定量仿真結果。 航天器再入隕落飛行過程中，隕落體的力學環境分析是非常困難的技術難點，而且力學環境和氣動加熱作用及材料物性密切相關。

3 三層級模型

為了對航天器再入隕落解體過程分析預報提供必要物形幾何前提，提出了一種新型簡潔的航天器再入隕落解體模型——三層級模型(Three Phases Model，TPM)。 該模型的基本思想是面向物體法，同時融入了面向航天器法的思維。

航天器再入隕落解體三層級模型的3 個層級是:①系統/子系統(Whole)；②部件(Part)；③碎片/微粒(Debris)。 因此，三層級模型又可稱為WPDM(Whole-Part-Debris Model)，如圖1 所示。

圖1 航天器再入隕落解體三層級模型Fig.1 Three phases model for spacecraft disintegration during reentry fall

航天器再入隕落解體三層級模型的系統/子系統，即指航天器整器形式。 對于中小型在軌運行航天器，可以是包括太陽能電池帆板或不包括太陽能電池帆板的形式；對于特大型在軌運行航天器，如國際空間站，顯然在某些隕落階段可以分為若干子系統。 通過實例分析可知，對航天器整器解體時刻的狀態參數，尤其是高度、速度、彈道傾角、飛行方位角的精確程度，對后續存活殘骸的落區范圍估計起到決定性作用，對殘骸存活性分析和地面風險評估也有影響。 這是三層級模型中特別指定系統/子系統層級的最大意義。

航天器再入隕落解體三層級模型的部件指的是航天器內部具有一定功能性及結構外形確定性的內容物，包括各種功能部件、氣瓶及燃料貯箱等。 當隕落至一定高度在氣動力/熱作用下，航天器整器外殼及附屬連接固定結構失效，其內部各部件在氣流沖擊下將飛散開來。 整器解體時刻參數即是各部件承受嚴苛氣動力/熱及運動分析的初始參數。 原則上，可以對具有確定幾何特性和質量特性的部件進行精細的氣動力/熱和運動分析，但是在熔融或燒蝕過程中，任何部件的幾何特性和質量特性的確定都是暫時性的。

4 塊條片模型

航天器再入隕落解體三層級模型的碎片/微粒指的是不可辨識原本幾何形態的殘留物。 碎片/微粒的來源有3 個方面:①航天器整器或部件熔融燒蝕后殘留物；②航天器整器或部件在氣流剪切撕扯下產生的碎片；③熔融物再凝結并得以存活的殘留物。 碎片/微粒的特征尺度下限根據關注的問題進行界定。 碎片/微粒的技術分析不再考慮氣動熱作用，即它們是被作為落地實物來看待的。 碎片/微粒的總量需封閉與航天器的質量守恒及材料屬性，同時考慮扣除燃燒或霧化湮沒的部分(一般情況下是絕大部分)。

碎片/微粒層級的外形建模過程中，對其幾何特征進行高度抽象。 幾何建模抽象基于完全歸納法原則，即可以覆蓋不同的幾何特征，從而覆蓋體現相應的氣動特性及飛行運動特性。 碎片/微粒按幾何特征分為3 類:①塊(Block)；②條(Column)；③片(Slice)。 因此，碎片/微粒層級的這種劃分模式可稱為塊條片模型(Block-Column-Slice Model， BCSM)。

3 類碎片/微粒的幾何形狀中(圖2)，塊以球或橢球指代，由短長軸比定形；片以半圓邊緣圓片指代，由厚度直徑比定形；條以半球端面圓柱指代，由長細比定形。 3 類碎片/微粒的尺度范圍(上下限)根據需要設定，塊由特征尺度長軸確定；條由特征尺度柱長確定；片由特征尺度直徑確定。 碎片/微粒的幾何形狀采用表面圓潤的設定，基于隕落殘骸歷經燒蝕及氣流沖刷后一般不再具有棱角分明的特征。

圖2 碎片/微粒層級的幾何建模Fig.2 Geometric modeling at debris/particle phase

碎片/微粒需滿足材料(密度)及對應總質量約束條件。 根據需要對3 類碎片/微粒的相關參數具體進行設定或覆蓋。 這些參數的設定和控制依賴于基礎研究成果對隕落解體過程的認識程度。

某些情況下，若系統/子系統及整器發生劇烈解體過程(如爆破等)，則部件級層級可能不存在，直接由系統/子系統層級演化至碎片/微粒層級。 在部件級存在情況下，某些碎片/微粒實體也可能由整器(主要是殼體)解體直接產生，這也是圖1 上部虛線的含義。

表1 定義了碎片/微粒的塊條片模型相關的幾何及材料屬性參數。

表1 碎片/微粒層級塊條片模型的幾何及材料屬性參數Table 1 Geometrical and material parameters of BCSM

對于每一個具體的碎片/微粒，其幾何及材料屬性確定的個體數量可表示為式(1)。

上述參量中，T 和M 為非連續性變量，R 和L為連續性變量，特別地，塊、條、片類型對應的個體數量可分別表示為式(2)。

連續性變量R 和L 一般可表示為在某種范圍內的分布函數的形式實際應用中根據需要進行離散化處理。 基于隕落過程中熔融及燒蝕作用具有使碎片外形圓潤化的趨勢，建議定形參數R 的取值下限為1，上限根據基礎研究和觀測結果的經驗積累進行評估確定。 此外，3 種碎片類型的定形參數為1 時，實際都歸化為基準的圓球形。 特征尺度L 必須具有明確的上下限，這是根據所關注的問題及實際研究對象的情況評估確定的。 具有相同材料屬性的任何類型碎片，應該滿足同一材料的質量約束條件。

碎片數量的關鍵依賴參數是特征尺度(或碎片質量)，根據類似研究[17-19]表明，碎片數量和特征尺度近似于指數變化規律，即尺度越小的碎片，其數量越多。 為此，構建特征尺度大于L 的碎片數量的表達式如式(3)所示。

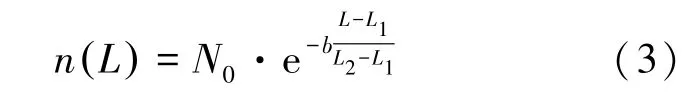
式中，N0為納入統計的碎片數量總數， b 為解體強度系數，L1和L2分別為碎片特征尺度的下限和上限，L 取值介于L1和L2之間。

以上碎片/微粒層級的塊條片模型，根據實際問題的工程要求情況，針對類別、定形、特征尺度和材料等方面，可以進行必要的簡并。

5 三層級模型的技術特點

航天器再入隕落解體三層級模型能夠涵蓋航天器解體研究對象的結構組成及碎片各種幾何特征，這些幾何外形特征能夠反映研究對象的氣動力/熱及飛行運動特性，通過調整參數的應用，針對航天器不同解體情況具有普遍適應性。

航天器再入隕落解體三層級模型的系統/子系統層級和部件層級具有面向航天器法的性質，碎片/微粒層級具有面向物體法的性質。 參照國內外現有方法模型，三層級模型具有如下特點:

1)融合了面向物體法和面向航天器法的思想，是該兩類方法的綜合體現；

2)三層級模型對研究對象結構定義清晰明確，更精煉適用，便于工程操作；

3)對系統/子系統的明確關注有利于精確分析航天器整器解體時刻的狀態參數；

4)對部件層級的定義有利于對隕落解體過程的細節情況進行探索；

5)碎片/微粒層級的塊條片模型能夠代表不同幾何特征及相應的氣動力/熱和飛行運動特性；

6)三層級模型能夠滿足工程分析需要，也有助于挖掘科學問題推進基礎研究。

6 基于條件邊界的參數統計方法

基于航天器再入隕落解體三層級模型，原則上對航天器再入隕落解體過程的分析預報提供了具體的研究對象，但是航天器再入隕落解體過程中的氣動力/熱現象實際上是外形及環境不斷變化的非定常問題，由此導致隕落過程必然是一個隨機過程。 換句話說，假設初始狀態完全相同的2 個隕落體，其隕落解體過程、殘骸存活情況及實際落區等都會有所不同。 對隨機過程的分析不能局限于確定性問題的解決思路，為此提出一種基于條件邊界的參數統計方法，作為航天器再入隕落分析預報的基本策略。

基于條件邊界的參數統計方法即是針對航天器再入隕落過程仿真建模分析中存在不確定性的氣動力/熱及飛行狀態參數，根據現有基礎研究成果評估確定其上下限即條件邊界；在隕落過程分析時，在這些條件邊界值域內，運用合適的參數分布及統計模型，對關注的目標參數進行定量分析。由此獲得統計意義上的航天器再入隕落過程及結果，這些結果應該是具有一定置信度的分布帶形式。

從飛行運動方面分析，由于質量特性對于隕落體往往是變化不定，很難把握的，且在高度100 km以上大氣極其稀薄、動壓非常小，航天器飛行過程的姿態轉動運動情況對平動運動幾乎不產生影響，一般情況下采用三自由度彈道方程即可。 但當需要把握解體前運動細節時可采用六自由度彈道方程。 基于三自由度橫向氣動力的需要，可把變形或局部破壞后的隕落體以及殘骸碎片的運動姿態參數納入合適的分布統計模型考慮。

從氣動力方面分析，在高超聲速條件下隕落體及其殘骸外形復雜且多變。 如果存在部分殘骸體接近地球表面且速度減至高超聲速以下，初步評估獲得的經驗表明，這類較低速度飛行的殘骸碎片不會在氣動力/熱作用下發生破壞，在這種情況下其當地彈道傾角一般已接近-90°，即其落點經過該類模式飛行后不會發生顯著變化。 因此，采用氣動力數據表或快速工程方法是沿彈道計算的主要選擇，必要的配平姿態評估可通過數值模擬分析，任何先進的大氣模型對大氣參數的推算也存在不確定度，故需要納入條件邊界參數統計的參量包括氣動阻力系數及大氣密度。

從氣動熱方面分析，由于對變形隕落體及殘骸碎片形狀的不確定性，對氣動分析的外形可以通過分類抽象模式化處理。 據此，對氣動熱直接相關參數進行參數分布統計已不存在邏輯上的必要性；實際上氣動熱的影響可轉化歸于對氣動力不確定度的影響。 對金屬材料部件的傳熱熔融計算及復合材料部件的熱解/燒蝕計算可采用零維或一維計算模型。

結構解體的分析是航天器再入隕落分析預報技術中最困難和最缺乏針對性基礎研究成果支撐的部分。 技術途徑是結合航天器再入隕落解體三層級模型，通過建立解體條件準則進行分析，即根據若干基礎研究的成果提煉相關的解體破壞判據。 可以考慮的解體條件準則包括:①高度準則，即設定在某一高度值發生某種形式的解體過程；②熔融準則，即設定金屬材料在達到熔融溫度發生某種形式的解體過程；③熱解準則，即設定復合材料在達到熱解溫度時發生某種形式的解體過程；④溫度準則，即認為物面溫度達到某一設定值將發生某種形式的解體過程；⑤熱流準則，即認為累計熱流或瞬時熱流達到某一設定值將發生某種形式的解體過程；⑥動壓準則，即認為動壓達到某一設定值將發生某種形式的解體過程；⑦時間準則，即設定在某一時刻發生某種形式的解體過程；⑧綜合準則，上述兩種或多種準則的綜合，可包括權重和、任一準則達成、全體準則達成等。

上述熔融準則及熱解準則可以認為是溫度準則和熱流準則的某種復合形式，但由于金屬材料在目前的航天器結構材料中占據最大百分比，故把熔融準則單列便于應用分析；復合材料則是目前航天器上有特殊要求的容器類的主要材料，因此也把熱解準則單列。

在DAS 和ORSAT 中，采用最簡單的高度準則預測解體；DRAPS 除了高度準則外還提供溫度準則、燒蝕準則(燒蝕到一定程度發生解體)和綜合準則(達到上述任何一個解體條件就認為解體)。 本文擬建立結構解體的較為系統完整的解體條件準則及解體形式的框架體系。 這些準則的選用根據實際的隕落過程特點；準則的量化建立依賴于實際研究的隕落體對象相關的基礎支撐成果的積累。

原則上，解體形式可以包括:①部件級解體，整器被肢解為部件；②碎片級解體，整器或部件被解體為碎片或微粒；③變形，外形發生變化。

由于外形變化在解體過程中是一種連續不斷的持續性過程，因此要對此進行精細分析或仿真是非常困難的；從關注解體結果的角度，可以把變形解體形式的影響納入其它解體條件的值域方面進行考慮。 結構解體分析中需要納入條件邊界參數統計的最重要的參量包括:解體碎片的尺度分布、解體碎片的形狀模式分布、解體高度范圍等。

隕落飛行過程中物體形狀及氣動力/熱局部參數的隨機性使得采用面向隕落體的完全有限元力/熱及結構應力耦合數值模擬代價巨大，需要大規模高性能并行計算，且其個別條件下的確定性數值分析結果并不能代表解體過程參數的隨機性。 但是，必須通過基礎研究成果來提煉工程上需要的支撐數據，并不斷深入研究逐步完善工程適用的解體判據。 如ORSAT 中默認的解體高度為78 km，然而本文研究表明，解體高度和研究對象材質及飛行模式關系密切，有必要進行精細化分析并設定合適的量化解體準則。

初步歸納，航天器再入隕落解體分析預報的基于條件邊界的參數統計方法涉及的統計分析參量如下:①隕落分析飛行起始參數，含初始位置三分量(坐標值x/y/z 或經度/緯度/高度)和初始速度三分量(速率/初始彈道傾角/初始方位角)，共6 個參量；②阻力系數；③大氣密度；④解體高度；⑤解體碎片尺度；⑥解體碎片形狀；⑦解體碎片姿態角。 上述12 個參數可根據情況進一步簡并，必要時也可擴展。 為了使用基于條件邊界的參數統計方法，需把握上述參數的基準值、不確定度及其分布形式，其中對結構解體相關參數的設定是最關鍵和最困難的。

7 實例應用分析

基于上述航天器再入隕落解體三層級模型及基于條件邊界的參數統計方法的分析策略及思路，開發研制了一套針對性的軟件系統。 軟件專門用于大型航天器再入隕落解體過程分析預報及地面風險評估，采用數據庫技術對軟件系統研究對象相關的素材資源、方法流程調度及結果數據進行綜合管理，并集成了各類相關基礎研究算法模塊。 圖3 為軟件系統基本邏輯流程圖，圖4 為軟件系統運行時的典型界面。

圖3 航天器再入隕落解體分析預報軟件系統基本流程圖Fig.3 Basic flow chart of analysis and prediction software system for spacecraft disintegration during reentry fall

圖4 航天器再入隕落解體分析預報軟件系統典型界面Fig.4 Typical interface of analysis and prediction software system for spacecraft disintegration during reentry fall

基于上述模型方法及開發的軟件系統，對一個大型航天器實例進行了初步分析。 由于相關基礎研究支撐工作是一個長期持續的過程，對解體模型中一些參數的邊界及分布設定還需要不斷細化和充實完善。

圖5(a)為用于隕落分析的大型航天器(簡稱LTG)，該航天器整器由一兩艙結構及兩側太陽能電池帆板組成。 艙體材質為鋁合金，部分組件外露艙體，包括中繼天線、軌控和姿控發動機噴管、各種相機光學窗口等。 圖5(b)為無太陽帆板的兩艙組合體，其與帶太陽帆板的整器共同構成算例應用分析中LTG 隕落解體三層級模型的系統/子系統層級。

圖5 LTG 隕落解體三層級模型之系統/子系統層級Fig.5 System/sub-system phase example of three phases model for a LTG spacecraft

LTG 再入隕落解體三層級模型的部件級大致包括了圖6 中的十多種類型，它們是組成該航天器的核心功能組件。 大部分內部部件由鋁合金材料構成，少量不銹鋼部件；軌控和姿控發動機噴管由鈮合金構成；還有部分由復合材料或碳纖維構成的瓶罐類容器；此外還有蓄電池模塊。

圖6 LTG 隕落解體三層級模型之部件層級Fig.6 Part phase example of three phases model for a LTG spacecraft

本例中，LTG 再入隕落解體三層級模型的碎片/微粒層級，簡化設定為球體、長方體、片類、桿類(長細比＝10)和桿類(長細比＝5)，并在此基礎上采用分組方法進行了統計計算分析。 圖7 為某設定條件下碎片落區的計算結果。

圖7 LTG 隕落解體三層級模型之碎片/微粒層級計算結果Fig.7 Debris/particle phase example of three phases model for a LTG spacecraft

針對LTG 再入隕落解體過程的系統建模和模擬，需要把握如下情況:隕落再入初始條件的確定；太陽電池帆板脫落的時機及對稱性；兩艙組合體逐漸熔融伴隨解體的復雜性；部件存活期間形變及氣動力熱局部參數的隨機性；燃料貯箱及電池模塊物理或化學爆破的可能性及影響。 上述情況的隨機性使得對整器解體的隕落分析的條件參數設置原則是盡量采取偏于保守的設定，包括對條件狀態參數基準值及其值域范圍，都需要在工程對象可能的范圍內進行綜合評估分析。

計算分析涉及的結果數據眾多，本文給出部分結果。 圖8 為LTG 兩艙組合體于高度100 km、迎角170°時表面溫度分布，此時其艙體迎風端面溫度已超過鋁合金材質熔點，熔融速率取決于當地熱流大小。

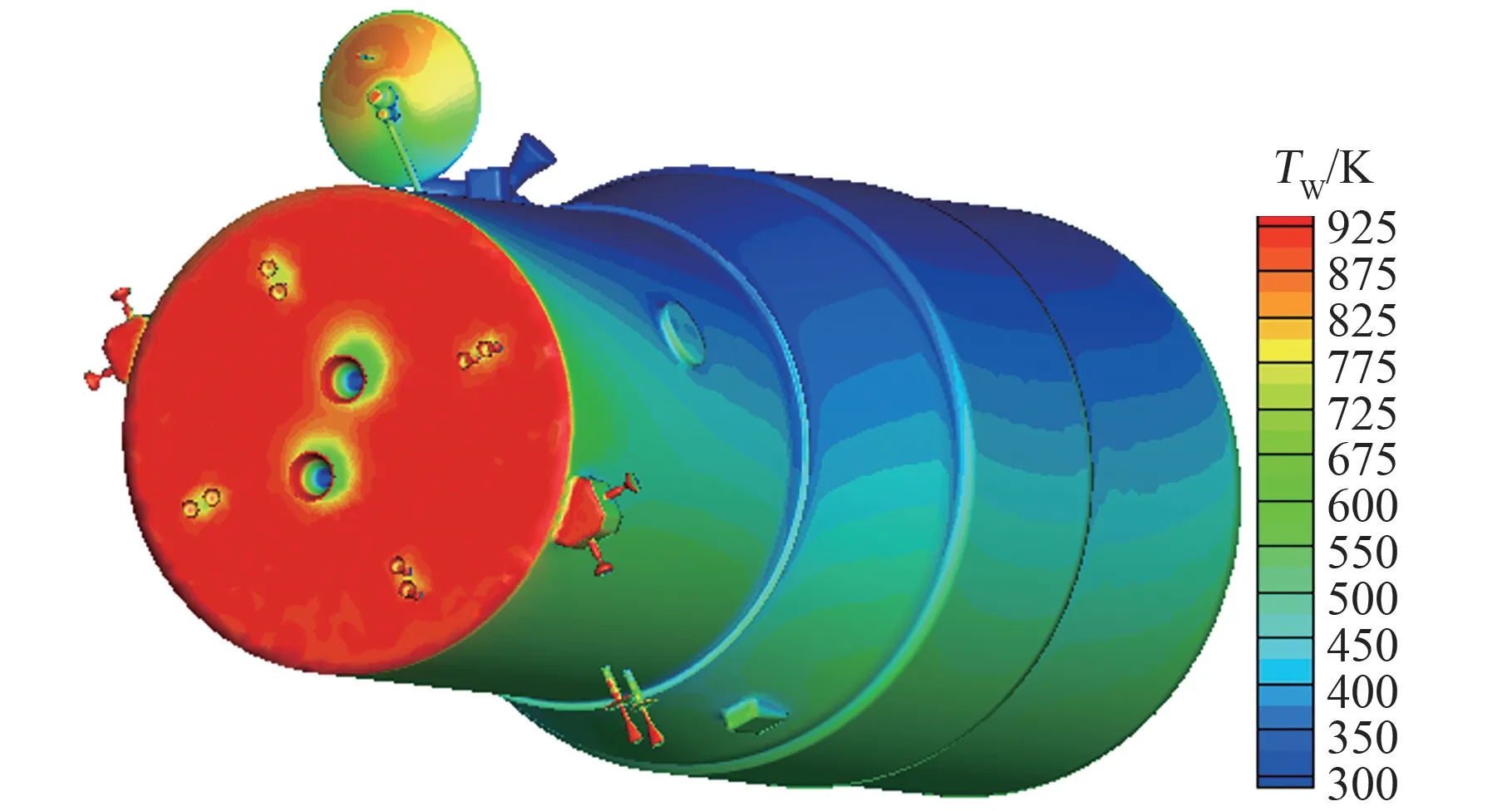
圖8 LTG 兩艙組合體表面溫度分布(高度100 km、迎角170°)Fig.8 Surface temperature distribution of LTG two cabin combination (hight is 100 km，angle of incidence is 170°)

圖9 給出了艙體解體后一些典型部件在飛行過程中的溫度、壓力、熱流等表面參數分布。 通過對這些部件組成材質(金屬類)的熔融情況分析，可以得出其最終存活性結論及落區范圍。

圖9 LTG 典型部件表面參數分布Fig.9 Surface parameter distribution of LTG typical components

根據計算結果分析表明，該大型航天器飛行至高度120 km 以下時，氣動力/熱即產生明顯作用。 在高度約105 km 處，太陽電池帆板在氣動力熱作用下脫落解體。 在高度約100 ～95 km 區間，由鋁合金構成的兩艙組合體殼體熔融解體，內部部件開始承受強烈氣動力/熱作用。 在高度約95～70 km 區間，鋁合金及不銹鋼部件分別熔融解體；碳纖維及復合材料部件熱解充分而解體。耐高溫合金組件如軌控發動機組和姿控發動機組，其合金材料在高度約60 km 處基本完全熔融，留存可辨識原本初始形態的殘骸落至地面的可能性極小，通常是經多次解體或熔融凝固殘骸、碎片墜落地面。 此外，兩艙解體后電池模塊在氣動熱作用下將很快因溫升發生爆破解體。

8 結論

1) 提出并闡述了航天器再入隕落解體三層級模型(TPM)(含碎片/微粒模型BCSM)以及基于條件邊界的參數統計方法。 該三層級模型融合了面向物體法涉及碎片/微粒層級和面向航天器法設計系統/子系統和部件層級的思想。

2) 針對航天器再入隕落解體過程仿真建模存在不確定性氣動力/熱及飛行狀態參數，發展了基于條件邊界的參數統計方法，通過相關軟件研制及對一個大型航天器實例的再入隕落解體過程分析，說明提出的模型和分析預報基本策略是合理可行的。

3) 后續工作將繼續細化量化三層級模型、條件邊界及參數分布統計等設定。 航天器再入隕落解體過程分析預報的精準度依賴于基礎研究成果的支撐程度，這是針對航天器再入隕落解體過程空氣動力學相關科學問題深入研究的驅動力。