節流孔數對空間熱泵徑向氣體軸承承載特性影響分析

李育隆，連華奇，徐向華，吳 宏

(1. 北京航空航天大學能源與動力工程學院，北京100191； 2.清華大學航天航空學院，北京100084)

1 引言

隨著航天技術的飛速發展，航天器規模和復雜程度與日俱增，導致航天器熱載荷急劇增加。國際空間站的總排熱功率已達到110 kW，要求熱控分系統輻射器的散熱能力達到150 kW。 可以預見，中國未來載人航天器的熱載荷以及熱排散需求必會呈數量級趨勢增加[1-3]。 如此大的熱排散需求，傳統的環路熱管、單項流體回路系統難以完全滿足。 以氟利昂為潤滑工質的氣體靜壓軸承作為支承的熱泵系統可以有效提高航天器的熱排散能力，同時又適用于空間微重力環境[4-5]。

靜壓氣體軸承的承載力來自外部高壓氣體經過節流器流入軸承間隙后形成的氣膜壓力，在微重力環境下受到的影響較小[6]。 而將靜壓氣體軸承應用于熱泵系統中，可以用熱泵壓縮機后的高壓氣體作為氣源，即可完成熱泵壓縮機的無油自潤滑，解決了傳統熱泵在微重力條件下的潤滑和密封問題。 然而，由于氟利昂氣體的粘性低于傳統的液體潤滑油，使氣體靜壓軸承的承載力低于傳統的液體潤滑軸承[7]，導致熱泵系統的穩定性能下降。 載人航天器由于內部有乘員，對其熱控系統的安全性、穩定性等設計要求都較高[8]。因此，提高靜壓氣體軸承的承載能力以保證空間熱泵壓縮機穩定運行是將空間熱泵技術運用到載人航天器上的關鍵。

提高孔式節流器的徑向氣體靜壓軸承承載力的方法主要集中在參數優化設計以及結構改進兩方面。 在結構改進方面，一種方法是采用主動控制技術控制節流，但會大幅度提升系統復雜度，不利于制造與安裝[9]。 而最簡單易行的是開設均壓槽方法，徑向氣體軸承在選用時，對其加工精度要求也稍高，故該方法優先應用于止推氣體軸承[10]。 在參數優化設計方面，減小軸承間隙、合理選取節流孔直徑均可以提高氣體軸承承載力，但是采用此方法的提升效果有限，而且減小軸承間隙對于加工精度的要求過高[11]。 而另一種方法是改變節流孔數，該方法加工難度小，也不會增加系統復雜度，適合應用于提高徑向氣體軸承承載力。 然而，目前不同節流孔數對徑向氣體軸承承載力的影響規律的研究還較少。 Yang 等[12]對于三孔以及六孔的徑向氣體軸承進行仿真，總結出不同排列方式的2 種氣體軸承的承載特性變化規律。 Chen 等[13-14]同樣對不同排列方式的三孔以及六孔的徑向氣體軸承進行仿真，研究了孔數對于氣體軸承穩定性的影響規律。 於陳程等[15]給出了估算節流孔數量對軸承靜態特性影響的一維模型，但是該模型在計算節流孔數量較小時的誤差較大。 楊濤等[16]在總結前人的基礎上，建立了空氣平面軸承節流器陣列的三維仿真模型，對不同節流孔數以及不同陣列排布的空氣平面軸承的承載力特性進行了研究。 Nishio 等[17]研究了密集排列的超小節流孔的止推軸承的承載性能與穩定性變化。

結合以上分析可以發現，改變節流孔數是增加徑向氣體軸承承載力的有效方法。 然而現有的研究中，節流孔數改變大的研究多是以止推氣體軸承為研究對象，而以徑向氣體軸承為研究對象時，節流孔數的變化范圍較小。 而且，對其他潤滑工質，尤其是以氟利昂氣體作為潤滑工質的研究極少。 針對以上問題，本文分別建立單排節流孔數N 為4、8、12、16、20 的徑向氣體軸承模型，以空氣和R134a 為工質研究徑向氣體軸承在不同工作狀態下的承載性能的變化。

2 數值模型

徑向氣體軸承結構如圖1 所示[18]，潤滑氣體先從節流孔流入軸承與軸的間隙中，再從軸承間隙的兩側流出，形成氣膜薄層分隔軸與軸承。 所研究的徑向氣體軸承選用環面孔式節流器以及雙排節流孔。

按所設計的實驗臺尺寸，計算中固定以下結構參數:軸承外徑D ＝28 mm，軸承總長L ＝28 mm，節流孔長度l0＝ 1.5 mm，節流孔中心線至軸承近端距離l ＝7 mm，節流孔直徑d0＝0.3 mm，平均軸承間隙h0＝25 μm，軸承偏心距e ＝12.5 μm 以及軸承偏心率ε ＝e/h0＝ 0.5。 此外，改變單排節流孔數N，分別取N 為4、8、12、16、20 進行建模研究，節流孔均沿周向平均分布，即相鄰節流孔的間距ψ 分別為90°、45°、30°、22.5°、18°，圖1(b)是以單排節流孔數N ＝ 8 為例的剖面圖。

圖1 徑向氣體軸承結構示意圖[18]Fig.1 Schematic diagram of journal gas bearing[18]

對徑向氣體軸承的流道進行建模后，采用結構化網格劃分模型，節流孔處使用O 型網格提高網格質量，在軸承的節流口底端與氣膜交界處以及近壁面處加密，同樣以N ＝ 16 為例，如圖2 所示。

圖2 徑向氣體軸承網格示意圖Fig.2 Mesh diagram of journal gas bearing

通過網格無關解之后得到的5 個不同節流孔數的模型的網格數量有所差異，如表1 所示。

表1 徑向氣體軸承網格數Table 1 Mesh number of journal gas bearing

潤滑氣體在氣膜薄層中流動時的雷諾數Re定義公式如式(1)[19]:

式中:ρ 為潤滑氣體密度；v 為潤滑氣體速度；μ 為潤滑氣體粘性系數；n 為旋轉軸轉速；ω 為轉子角速度。 取n ＝140 000 r/min， 取潤滑氣體為空氣，得到Re ≈282.1。 旋轉軸轉速n ≤140 000 r/min 時，即在本文計算工況下，潤滑氣體流速遠小于該情況下的氣體流速，可知Re ?282.1，因此選用層流的流動模型。

研究采用商業軟件Fluent 計算求解，控制方程選用添加能量方程的三維N-S 方程，考慮粘性耗散，絕熱壁面。 當全場殘差小于10-5時，認為計算收斂至真值，空氣模型選用可壓縮的理想氣體模型，氟利昂氣體模型選用NIST 的真實氣體模型，在計算中物性參數隨溫度變化而變化[20]。

在節流孔的進口處設定壓力和溫度作為進口條件，進口溫度的改變對計算結果的影響遠小于改變單排節流孔數的影響，因此固定進口溫度T ＝300 K。 在氣膜層兩側出口設定背壓為1 atm的出口條件。 仿真計算時，固定旋轉軸轉速n ＝0 r/min，改變軸承的進氣壓力p ＝2 ～7 atm，即得到不同節流孔數在靜止狀態的承載特性。 固定軸承的進氣壓力p ＝6 atm， 改變旋轉軸轉速n ＝0 ～140 000 r/min，即得到不同節流孔數在旋轉狀態的承載特性。

3 計算結果分析

3.1 靜止狀態的承載特性

在靜止狀態下，即當旋轉軸轉速n ＝ 0 r/min時，改變軸承的供氣壓力，得到不同節流孔數的徑向氣體軸承隨供氣壓力變化的承載特性曲線。

圖3 是以空氣為工質時，不同節流孔數的徑向氣體軸承在靜止狀態下的承載力和質量流量隨供氣壓力的變化曲線圖。 其中，徑向氣體軸承的靜承載力是將軸承氣膜層內壁面壓力進行曲面積分得到，直觀反映了徑向軸承的承載性能。 從圖3(a)可以看出，當徑向氣體軸承的工質為空氣時，徑向氣體軸承的承載力并不是隨節流孔數的增加而單向增加的。 當軸承的供氣壓力較小時，取N ＝12，軸承的承載力最大，增加或減小節流孔數，其承載力均會下降。 隨著供氣壓力的增加，使軸承承載力達到極大值的節流孔數也隨之增加。 在仿真計算的范圍內，當N ＞12 時，增加節流孔數對軸承承載力的提升效果較差。 在理想情況下，取單排節流孔數為無限大，則節流孔連成一條狹縫，即為狹縫節流，此時的承載力也達到最大值。 結合圖3(a)展現的規律可知，圖3(a)中展現的使軸承承載力達到極大值的節流孔數，即為使軸承承載力達到最大值所需的最小節流孔數。而圖3(a)中展現的繼續增加節流孔數會導致承載力出現微量下降的規律，是由于數值仿真存在數值誤差和不確定度。 圖3(b)中表明，隨著供氣壓力和節流孔數的增加，徑向氣體軸承所需的質量流量隨之增加。 綜上所述，若為了得到較高的承載力，可以提高供氣壓力，以及增加節流孔數；而為了增加氣體軸承的經濟性，則應盡量取氣體軸承的單排節流孔數N ＝8 ～12。

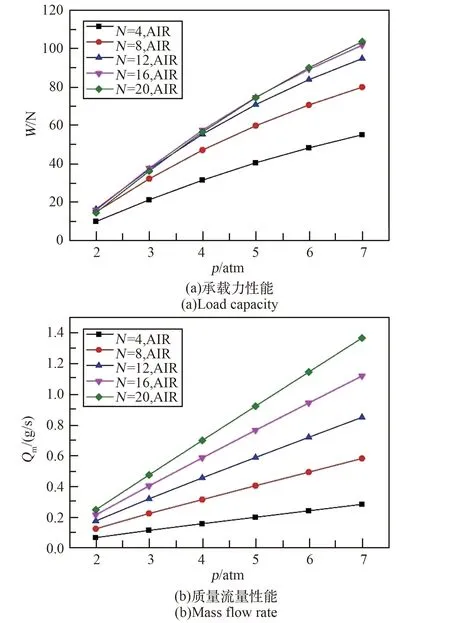
圖3 工質為空氣時氣體軸承的承載性能(靜止狀態)Fig.3 Characteristics of gas bearing with air (static)

圖4 是以R134a 為工質時，不同節流孔數的徑向氣體軸承在靜止狀態下的承載力和質量流量隨供氣壓力的變化曲線圖。 圖4 表明，以R134a為工質時，增加節流孔數必定能夠增大承載力。同樣地，當N ＞12 后，承載力的增大幅度減小，但是其質量流量的增大幅度并未有明顯的減小。 綜上所述，選用R134a 作為工質時，為了在獲得較大承載力的同時，消耗盡量少的質量流量，同樣應取N ＝8 ～12。

圖4 工質為R134a 時氣體軸承的承載性能(靜止狀態)Fig.4 Characteristics of gas bearing with R134a(static)

3.2 旋轉狀態的承載特性

固定徑向軸承的進氣壓力p ＝6 atm，改變軸承的旋轉軸轉速，得到不同節流孔數的徑向氣體軸承隨轉速變化的承載特性曲線。

圖5 是以空氣為工質時，不同節流孔數的徑向氣體軸承在旋轉狀態下的承載力和質量流量隨轉速的變化曲線圖。 從圖5(a)中可以發現，當轉速增加時，軸承的承載力也隨之增加。 這是由于徑向軸承存在偏心，其氣膜厚度在周向上存在變化；旋轉軸轉動，潤滑氣體在軸承間隙中隨旋轉軸流動，產生動壓效應。 此時軸承不止依靠靜壓效應提供承載，也依靠動壓效應提供承載，且隨著轉速的增加，動壓效應也相應增強。

此外，可以看出當轉速n ≤20 000 r/min，當單排節流孔數N ＝20 時，氣體徑向軸承的承載力達到最大；而20 000 r/min ＜n ≤100 000 r/min 時，取N ＝16， 軸承的承載力達到最大；而當轉速n ＞100 000 r/min 時，取N ＝12，軸承的承載力達到最大。N ＝8 以及N ＝4 時的承載力一直都是最低的，但轉速增加后，其承載力與節流孔數增多后的承載力的差距減小。 由此表明，在低轉速工況下，節流孔數的增加會增加軸承的承載力；在高轉速工況下，在節流孔數達到某一特定值后，增加節流孔數反而會使軸承的承載力降低。

而從圖5(b)中發現，以空氣為工質，且供氣壓力固定時，影響氣體軸承質量流量的最主要因素是單排節流孔數。 單排節流孔數越大，徑向氣體軸承所需的氣體的質量流量就越大。 隨著轉速的增加，徑向氣體軸承所需的質量流量雖然會降低，但下降幅度極小。

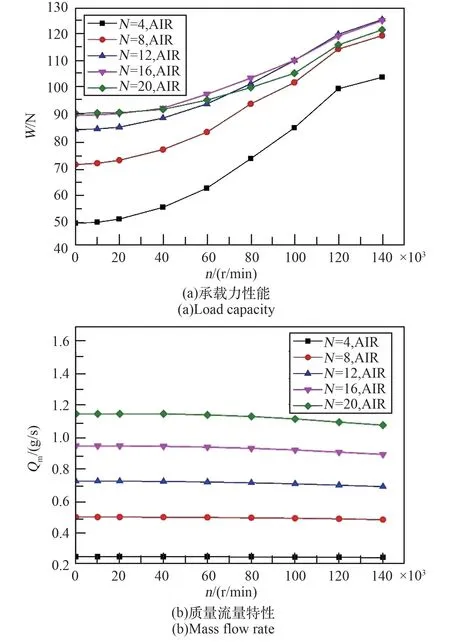
圖5 工質為空氣時氣體軸承的承載性能(旋轉狀態)Fig.5 Characteristics of gas bearing with air (rotating)

綜上所述，徑向氣體軸承以空氣為工質時，在高轉速( n ≥80 000 r/min)工況下，選用較小的單排節流孔數N 可以得到較好的承載性能；在低轉速工況( n ＜80 000 r/min)下，選用較大的單排節流孔數N 可以得到較好的承載性能，即系統的工作轉速越高，則設計階段選用的單排節流孔數N 越小。

觀察轉速n ＝120 000 r/min 時，徑向氣體軸承沿軸承長度方向的中心對稱面上的壓力分布如圖6 所示，隨著節流孔數的增多，軸承在周向上任意位置的壓力均會升高。 從壓力分布曲線上可以得知，不同節流孔數的徑向氣體軸承均在周向80°～120°范圍內達到氣膜內部壓力的極大值。對于徑向氣體軸承而言，其承載力主要來源于氣膜層上下兩部分的壓力差，即0°～180°區域的壓力矢量和與180°～360°的壓力矢量和。 在0°～180°的高壓區，壓力值隨節流孔數增大的幅度相對較小，但180°～360°的低壓區域，壓力值隨節流孔數增大的幅度較大，使得節流孔數增加后，上下表面壓差反而減小，最終導致在該轉數下，在節流孔數達到某一特定值N ＝12 后，增加節流孔數反而會使軸承的承載力降低。

圖6 當n＝120 000 r/min 時軸承長度方向對稱線上的壓力周向分布Fig.6 Pressure distribution on symmetry line in the direction of bearing length when n＝120 000 r/min

對比分析工質為R134a 時徑向氣體軸承的承載性質，發現與工質為空氣時存在很大不同。圖7 是以R134a 為工質時，不同節流孔數的徑向氣體軸承在旋轉狀態下的承載力和質量流量隨轉速的變化曲線圖。 從圖7(a)中發現，無論是高轉速還是低轉速下，徑向氣體軸承的承載力均隨節流孔數的增大而增大。

圖7 工質為R134a 時氣體軸承的承載性能(旋轉狀態)Fig.7 Characteristics of gas bearing with R134a (rotating)

軸承承載力隨節流孔數的增長率定義如式(2)所示。

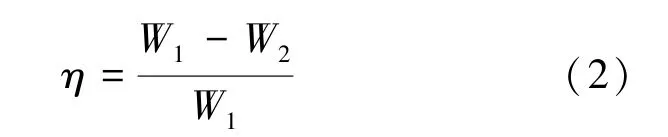
式中，W1為單排節流孔數為N 時的承載力，W2為單排節流孔數為N ＋4 時的承載力，得到的η 認為是單排節流孔數為N 時的承載力增長率。

從表2 可以得知，同一轉速下，節流孔數越多，增加節流孔數后，承載力增長率越小，即增加節流孔數量得到的效益越低。 而在同一節流孔數下，隨著轉速的增加，承載力增長率也不斷減小。這表明，隨著轉速增加，節流孔數少的氣體軸承與節流孔數多的軸承的承載力更接近，即節流孔數越小，其承載力隨轉速增大的幅度越大，其動壓效應越明顯。

表2 不同轉速下的承載力增長率表Table 2 Increase rate of bearing capacity at different rotation speed

結合圖7(b)所顯示的節流孔數越多，其質量流量越大的性質。 綜合分析得到，當徑向氣體軸承以R134a 為工質時，同樣滿足轉速越高，則設計階段選用的單排節流孔數N 越小的原則。

4 結論

本文針對以空氣和氟利昂氣體為潤滑工質的徑向氣體軸承，采用數值模擬的方法研究了不同節流孔數以及工作狀態對徑向氣體軸承的靜承載力、質量流量特性的影響，得到了以下結論:

1) 對靜止狀態的徑向氣體軸承，其承載力隨著節流孔數的增加而增加，但節流孔數越多，增加節流孔數后承載力提高的幅度越小。

2) 本文轉速研究范圍內的旋轉徑向氣體軸承，低轉速( n ＜80 000 r/min)工況下，應選用較大的節流孔數( N ＞12)以獲得較好的承載力性能；高轉速( n ≥80 000 r/min)工況下，應選用較小的節流孔數( N ≤12)以獲得較好的承載力性能。 因此，取N ＝12， 可以兼顧靜態和動態的軸承承載力。

3) 徑向氣體軸承的質量流量會隨著節流孔數的增加而增加，同時也會隨進氣壓力的增加而增加，而轉速對于其質量流量的影響較小。