黃河三角洲鹽堿土微觀孔隙特征的分形研究

李克升,劉傳孝,李全新,耿雨晗

山東農(nóng)業(yè)大學(xué)水利土木工程學(xué)院,山東 泰安 271018

土體的物理力學(xué)性質(zhì)在很大程度上取決于其微觀結(jié)構(gòu)[1-5]。土體孔隙作為滲透的通道，其大小、分布和迂曲程度將直接影響土體滲透性[6]。因此，應(yīng)用微觀測(cè)試技術(shù)結(jié)合分形幾何學(xué)理論來(lái)探索土體的微觀孔隙特征，進(jìn)而研究土體的物理力學(xué)性質(zhì)是必要的。近年來(lái)，掃描電鏡（SEM）、CT、壓汞法（MIP）和能譜（EDS）等新技術(shù)的發(fā)展，給土體微觀結(jié)構(gòu)的研究提供了豐富的技術(shù)手段[7-9]。此外，國(guó)內(nèi)外學(xué)者對(duì)分形幾何學(xué)的進(jìn)一步探索也為定量表征土體結(jié)構(gòu)的復(fù)雜程度提供了理論依據(jù)。

國(guó)內(nèi)外學(xué)者采用不同的微觀測(cè)試手段和分形模型對(duì)不同土體的微觀孔隙特征、土體結(jié)構(gòu)的復(fù)雜程度和分形維數(shù)與微觀參數(shù)的關(guān)系進(jìn)行了深入研究，取得了大量的成果。Lu Y,et al.基于掃描電鏡試驗(yàn)對(duì)凍融循環(huán)條件下黏性土的裂縫進(jìn)行了分形幾何研究，發(fā)現(xiàn)分形維數(shù)與表面裂縫率有良好的相關(guān)性[10]。Zhou J,et al.在分形和概率分析的基礎(chǔ)上，建立了軟粘土凍融效應(yīng)綜合雙孔隙度計(jì)算模型，并對(duì)該模型的應(yīng)用進(jìn)行了探討[11]。Atzeni C,et al.對(duì)多孔材料的孔隙結(jié)構(gòu)采用Pfeifer 和Avnir 方法確定了實(shí)驗(yàn)數(shù)據(jù)集的分形維數(shù)，發(fā)現(xiàn)P 海綿模型比Menger 海綿模型更具有代表性[12]。Delage P,et al.對(duì)Champlain 黏土開(kāi)展壓汞試驗(yàn)，定量分析孔徑分布隨固結(jié)壓力的變化，至此壓汞試驗(yàn)已成為研究土體微觀結(jié)構(gòu)的重要手段[13]。孫秀麗等利用掃描電鏡（SEM）和分形幾何理論對(duì)疏浚淤泥固化土的孔隙結(jié)構(gòu)進(jìn)行了定量研究，確定了分形維數(shù)與微觀結(jié)構(gòu)參數(shù)、宏觀力學(xué)性質(zhì)以及固化材料比例之間的關(guān)系[14]。劉風(fēng)華等采用CT 技術(shù)研究了渠道邊坡膨脹土的微觀結(jié)構(gòu)，從分形幾何角度研究其內(nèi)部裂隙規(guī)則度，發(fā)現(xiàn)膨脹土內(nèi)部裂隙具有明顯的不規(guī)則性[15]。楊明輝等引入分形理論，對(duì)非飽和土的孔隙及通道分布的非均質(zhì)性及瓶頸效應(yīng)進(jìn)行了模擬，探討了非飽和土吸濕與脫濕過(guò)程中的土水特征曲線的滯后效應(yīng)以及滲透規(guī)律[16]。陶高梁等通過(guò)壓汞試驗(yàn)對(duì)武漢黏性土的孔隙特征進(jìn)行研究，發(fā)現(xiàn)不同干密度土樣均存在臨界孔徑現(xiàn)象，且臨界孔徑前后孔隙分布規(guī)律有顯著區(qū)別[17]。陳毅等采用壓汞法（MIP）和掃描電鏡法（SEM）分別對(duì)定西市遺址土內(nèi)外部土樣的微觀孔隙結(jié)構(gòu)進(jìn)行研究并引入分形理論對(duì)其孔隙特征進(jìn)行評(píng)價(jià)，研究表明隨著風(fēng)化時(shí)間的增長(zhǎng)，外部土體的孔隙總體積和表面分形維數(shù)逐漸減小[18]。

上述研究成果證明分形理論能較好地描述土體孔隙結(jié)構(gòu)的復(fù)雜性和不規(guī)則性，但前人的研究主要集中于采用單一的分形模型來(lái)描述土體孔隙結(jié)構(gòu)，并且忽略了不同分形模型對(duì)不同土體的適用性問(wèn)題。此外，前人所采用的分形模型均假設(shè)孔隙是光滑的圓柱體，無(wú)法準(zhǔn)確地描述土體真實(shí)的孔隙結(jié)構(gòu)特征。因此本文以廣饒縣農(nóng)田鹽堿土為研究對(duì)象，壓汞試驗(yàn)為技術(shù)手段，探索不同深度鹽堿土孔隙的迂曲程度，并根據(jù)分形幾何學(xué)理論優(yōu)選出體積分形模型。研究結(jié)果可提高對(duì)該地區(qū)鹽堿土微觀孔隙特征的認(rèn)識(shí)，為揭示鹽堿土的滲透性和鹽堿地修復(fù)提供參考。

1 材料與方法

2.1 試驗(yàn)材料

試驗(yàn)土樣取自山東省東營(yíng)市廣饒縣美奧生物有限公司（37°18′7″N,118°38′7″E）附近，如圖1 所示。在取樣過(guò)程中，采用環(huán)刀法取樣以保證試驗(yàn)土樣的原始結(jié)構(gòu)不被破壞。試驗(yàn)取樣深度范圍為0～60 cm，分別取深度為0、10、20、30、40、50 和60 cm 處的均質(zhì)土樣作為微觀結(jié)構(gòu)分析的樣品。

1.2 試驗(yàn)方法及原理

根據(jù)《土工試驗(yàn)規(guī)程》規(guī)定，采用變水頭試驗(yàn)測(cè)試不同深度土壤的滲透系數(shù)。取不同深度的土樣，將其制成5 mm×5 mm×10 mm 的長(zhǎng)方體，試驗(yàn)采用真空冷凍干燥法（如圖2a 所示）除去土樣中的水分；并采用美國(guó)康塔儀器公司生產(chǎn)的全自動(dòng)壓汞儀PM-33-18 進(jìn)行壓汞試驗(yàn)（如圖2b 所示）。

壓汞法是在一定壓力下將汞壓入到介質(zhì)中，根據(jù)壓力和壓入汞的體積換算出各類(lèi)孔隙的大小，壓汞法是分析土體微觀結(jié)構(gòu)最通用的方法。壓汞法的原理是非浸潤(rùn)性液體在沒(méi)有壓力時(shí)不會(huì)流入固體孔隙，圓柱形孔隙注入液體所需壓力大小根據(jù)Washburn 公式計(jì)算[19]：

式中：P為施加壓力，Pa；σ為浸入液體的表面張力系數(shù)，N/m；θ為導(dǎo)入液體與固體材料的接觸角，°；r為圓柱形孔隙半徑，m。

根據(jù)相關(guān)的文獻(xiàn)[20]，取σ=0.485 N/m，θ=140°。從壓汞結(jié)果中可以得到壓力與進(jìn)汞體積之間的關(guān)系，利用公式（1），通過(guò)壓力P求得對(duì)應(yīng)的當(dāng)量直徑d，以此轉(zhuǎn)換得到土的孔隙分布和表面積等孔隙特征參數(shù)。

2 鹽堿土孔隙分形模型

2.1 空間填充模型

Ji X,et al.根據(jù)水泥混凝土發(fā)生水化反應(yīng)填充大孔隙生成小孔隙的原理構(gòu)造了空間填充模型，經(jīng)過(guò)大量的試驗(yàn)證實(shí)，空間填充模型同樣適應(yīng)于土體的分形研究。空間填充模型的詳細(xì)推導(dǎo)過(guò)程可參考文獻(xiàn)[21]，計(jì)算公式為：

V為累積孔隙體積，cm3/g；t為常數(shù)；r為孔隙半徑，m；DK為基于空間填充模型的分形維數(shù)。

根據(jù)壓汞試驗(yàn)測(cè)定的累積孔隙體積V與孔隙半徑r分別取對(duì)數(shù)后得到的直線斜率，即可求得分形維數(shù)DK。

2.2 Menger 海綿模型

Menger 海綿模型是研究固體材料分形維數(shù)最常用的模型之一，其具體的推導(dǎo)過(guò)程可參考文獻(xiàn)[22]，計(jì)算公式為：

V為累積孔隙體積，cm3/g；k為比例常數(shù)；DL為基于Menger 海綿模型的分形維數(shù)；P為進(jìn)汞壓力，MPa。

根據(jù)壓汞試驗(yàn)的結(jié)果，以log（dV/dP）為縱坐標(biāo)，以logP為橫坐標(biāo)，求得擬合直線的斜率，即可求得分形維數(shù)DL。

2.3 毛細(xì)管壓力曲線法模型

根據(jù)毛細(xì)壓力對(duì)數(shù)與濕潤(rùn)相飽和度對(duì)數(shù)的線性關(guān)系可求得孔隙的分形維數(shù)，其具體的推導(dǎo)過(guò)程可參考文獻(xiàn)[23]，計(jì)算公式為：

S為孔徑小于r的累積孔隙體積百分比，%；DM為基于毛細(xì)管壓力曲線法的分形維數(shù)；Pmin為最大孔徑對(duì)應(yīng)的毛管壓力，MPa；P為孔徑為r所對(duì)應(yīng)的壓力，MPa。

根據(jù)壓汞試驗(yàn)結(jié)果，以logS為縱坐標(biāo)，以lgP為橫坐標(biāo)，對(duì)不同深度鹽堿土壓汞試驗(yàn)中進(jìn)汞過(guò)程中的數(shù)據(jù)進(jìn)行線性擬合，求得擬合直線的斜率，即可求得分形維數(shù)DM。

2.4 熱力學(xué)模型

熱力學(xué)模型是由張玉良等人推導(dǎo)得出的，其具體的推導(dǎo)過(guò)程可參考文獻(xiàn)[24]，計(jì)算公式為：

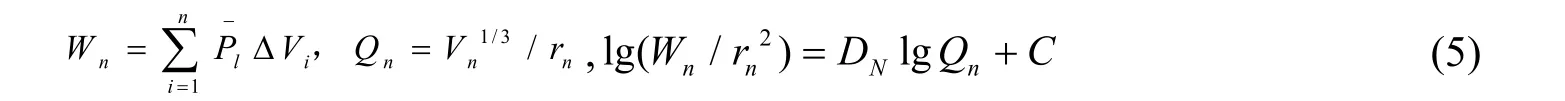
Pl為第i次進(jìn)汞的平均壓力，MPa；ΔVi為第i次進(jìn)汞增量，cm3/g；n為施加壓力的間隔次數(shù)；rn為第n次進(jìn)汞時(shí)對(duì)應(yīng)的孔隙半徑，nm；DN為基于熱力學(xué)模型的分形維數(shù)。

根據(jù)壓汞試驗(yàn)結(jié)果，以lg（）為縱坐標(biāo)，以lgQn為橫坐標(biāo)，對(duì)不同深度鹽堿土壓汞試驗(yàn)中進(jìn)汞過(guò)程中的數(shù)據(jù)進(jìn)行線性擬合，求得擬合直線的斜率，即可求得分形維數(shù)DN。

2.5 孔軸線模型

孔軸線模型是由尹紅宇以Von koch 曲線模型為基礎(chǔ)所提出的，具體的推導(dǎo)過(guò)程可參考文獻(xiàn)[25]，計(jì)算公式為：

V為累積孔隙體積，cm3/g；DT為基于孔軸線模型的分形維數(shù)；r為孔隙半徑，nm。

根據(jù)壓汞試驗(yàn)結(jié)果，以lg（d2V/dr2）為縱坐標(biāo)，以lgr為橫坐標(biāo)，對(duì)不同深度鹽堿土壓汞試驗(yàn)中進(jìn)汞過(guò)程中的數(shù)據(jù)進(jìn)行線性擬合，求得擬合直線的斜率，即可求得分形維數(shù)DT。

3 結(jié)果與分析

3.1 基于不同分形模型的分形維數(shù)計(jì)算

利用上述5 種分形模型計(jì)算公式處理不同深度鹽堿土的壓汞數(shù)據(jù)，并計(jì)算其分形維數(shù)。圖3 為不同分形模型所計(jì)算的40 cm 深度處鹽堿土孔隙的分形維數(shù)，其它深度鹽堿土孔隙的分形維數(shù)計(jì)算結(jié)果見(jiàn)表1。由分形幾何學(xué)理論可知，多孔介質(zhì)的孔隙結(jié)構(gòu)分形維數(shù)的合理范圍為2～3，分形維數(shù)反映研究對(duì)象的復(fù)雜程度，分形維數(shù)越大，說(shuō)明研究對(duì)象復(fù)雜程度越高。

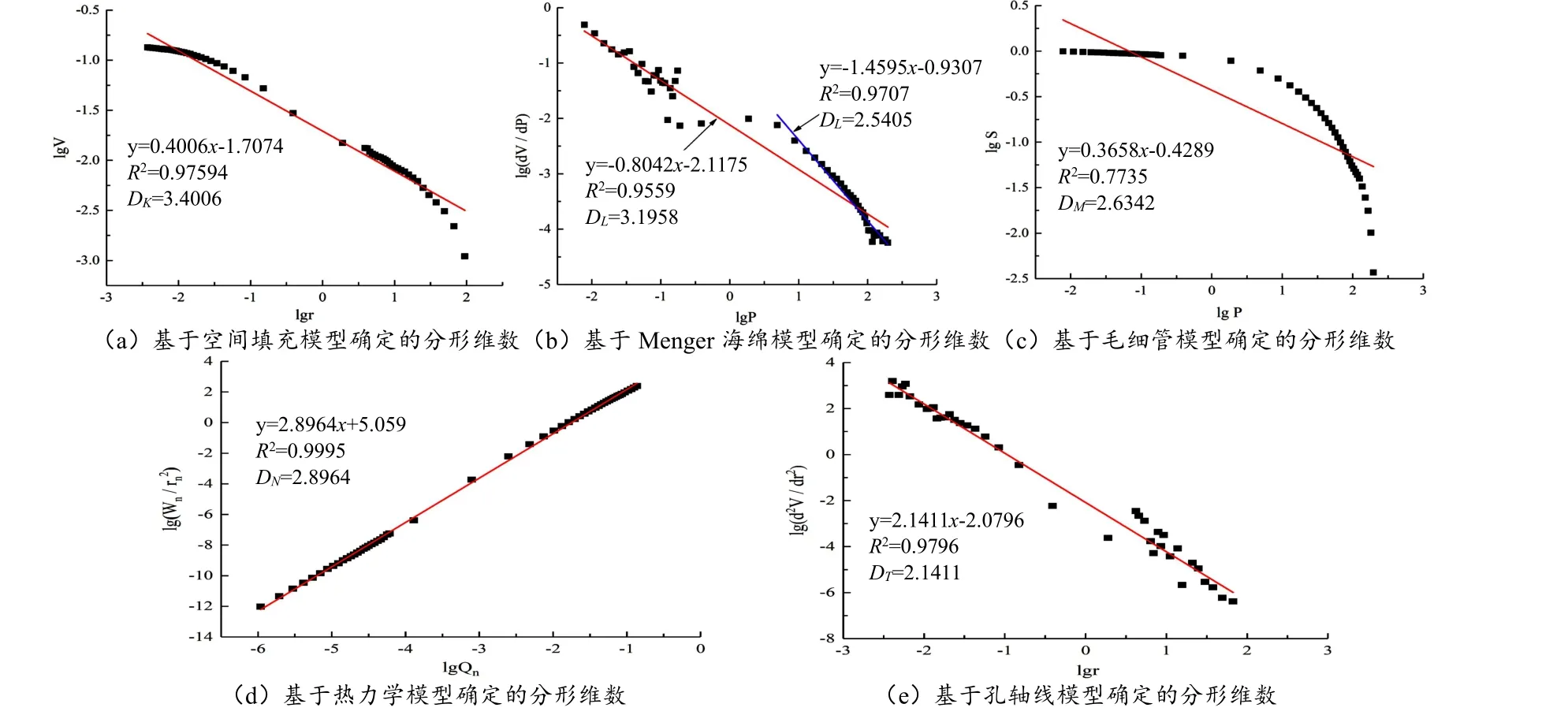
圖3 40 cm 深度處土樣的分形維數(shù)計(jì)算Fig.3 Fractal dimension calculation of soil sample at 40 cm depth

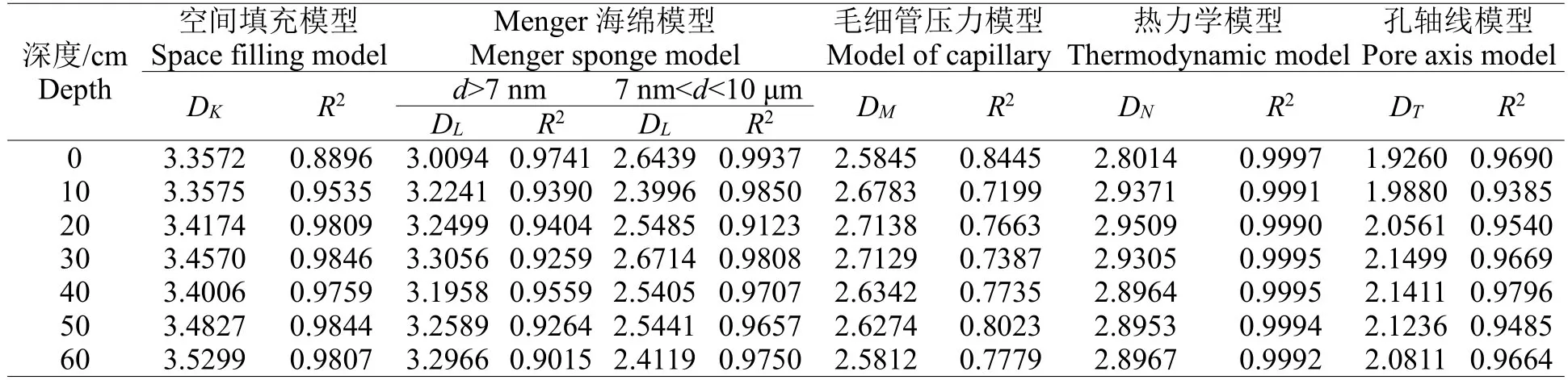
表1 不同深度土樣的分形維數(shù)計(jì)算結(jié)果Table 1 Calculation results of fractal dimension of soil samples with different depths

3.2 基于孔軸線分形模型的孔隙結(jié)構(gòu)特征分析

孔軸線模型是在Von koch 孔隙模型的基礎(chǔ)上所提出來(lái)的，它被用來(lái)描述孔隙彎曲的復(fù)雜程度，因此由此模型所得分形維數(shù)的取值大于0 即可，并且分形維數(shù)越大，代表孔隙的彎曲程度越復(fù)雜，孔隙曲率越大，滲透系數(shù)越低。由圖3（e）和表1 可知，lg（d2V/dr2）與lgr呈較好的線性相關(guān)，線性相關(guān)系數(shù)在0.9385～0.9796 之間。不同深度鹽堿土孔隙結(jié)構(gòu)擬合所得的分形維數(shù)DT在1.9260～2.1499 之間變化，且隨深度的增加，孔軸線模型確定的分形維數(shù)呈現(xiàn)先增加后減小的趨勢(shì)。由此可見(jiàn)，該研究區(qū)域內(nèi)鹽堿土孔隙彎曲程度較大，這也是其滲透性差的原因之一。

孔軸線模型所確定的分形維數(shù)與土壤滲透系數(shù)的關(guān)系如圖4 所示。由圖4 可以看出，孔軸線模型所確定的分形維數(shù)與土壤滲透系數(shù)之間表現(xiàn)出良好的負(fù)相關(guān)性，這說(shuō)明隨著孔軸線迂曲程度增加，土壤滲透系數(shù)逐漸減小。農(nóng)田鹽堿土的滲透系數(shù)在4.35～10.15 mm/h 之間，這說(shuō)明農(nóng)田鹽堿土的滲透能力較低，這為鹽堿地的治理帶來(lái)了較大的阻力。

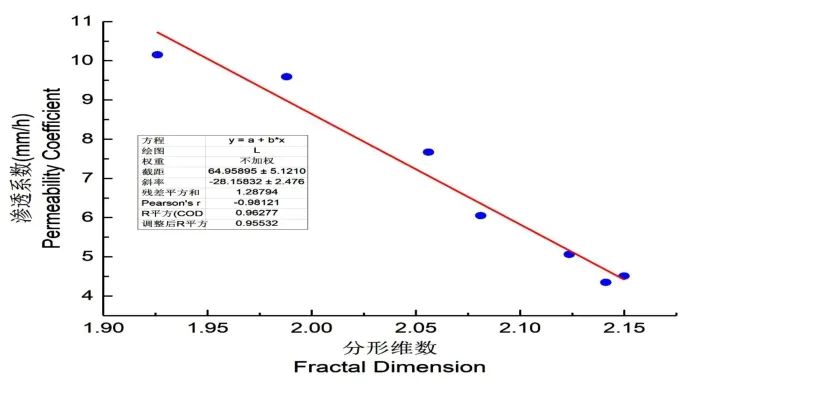
圖4 土壤滲透系數(shù)與分形維數(shù)DT 的關(guān)系Fig.4 Relationship between soil permeability coefficient and fractal dimension DT

3.3 基于體積分形模型的孔隙結(jié)構(gòu)特征分析

空間填充模型確定不同深度鹽堿土的分形維數(shù)時(shí)，lgr與lgV呈較好的線性相關(guān)，線性相關(guān)系數(shù)在0.8896～0.9846 之間，但分形維數(shù)DK均大于3，這說(shuō)明黃河三角洲鹽堿土孔隙結(jié)構(gòu)相當(dāng)復(fù)雜且無(wú)序，已經(jīng)超出歐氏三維空間理論范疇，僅能用分形維數(shù)來(lái)進(jìn)行闡明。根據(jù)經(jīng)典幾何觀點(diǎn)可知其明顯偏離了分形維數(shù)的合理定義，因此空間填充模型不能定量表征鹽堿土孔隙結(jié)構(gòu)的復(fù)雜程度。

Menger 海綿模型確定不同深度鹽堿土的分形維數(shù)時(shí)，lg（dV/dP）與lgP呈線性相關(guān)，線性相關(guān)系數(shù)較高，但由其確定的分形維數(shù)均大于3（如表1 所示），因此Menger 海綿模型不能在整體孔徑尺度范圍內(nèi)定量表征鹽堿土孔隙結(jié)構(gòu)的復(fù)雜程度。孔隙的孔徑在7 nm～10 μm 區(qū)間時(shí)，Menger 海綿模型所確定的分形維數(shù)DL在2.3996～2.6714 之間且線性相關(guān)系數(shù)在0.9 以上。由此可以看出，Menger海綿模型僅能較好表征鹽堿土孔徑在7 nm～10 μm 區(qū)間內(nèi)的孔隙分形特征。

毛細(xì)管壓力法模型確定不同深度鹽堿土的分形維數(shù)時(shí)，lgS與lgP分階段線性相關(guān)，這表明在不同孔隙直徑區(qū)間范圍內(nèi)鹽堿土孔隙具有不同的自相似度。從整體孔徑尺度范圍來(lái)看，不同深度鹽堿土孔隙的分形維數(shù)DM在2.5812～2.7138 之間，線性相關(guān)系數(shù)在0.8 左右。盡管lgS與lgP的線性相關(guān)系數(shù)較低，但分形維數(shù)在合理范圍內(nèi)，因此采用毛細(xì)管壓力法模型確定的分形維數(shù)在一定程度上仍可定量表征鹽堿土孔隙結(jié)構(gòu)的復(fù)雜程度。

以上4 種體積分形模型中，空間填充模型所確定的分形維數(shù)不能有效表征孔隙的分形特征；Menger 海綿模型僅能定量表征孔徑在7 nm～10 μm 區(qū)間內(nèi)的孔隙分形特征；在使用毛細(xì)管壓力法模型確定分形維數(shù)時(shí)，沒(méi)有充分考慮實(shí)際進(jìn)汞過(guò)程中間隔施加壓力所得到的數(shù)據(jù)點(diǎn)不夠密集的情況，導(dǎo)致在整體孔徑尺度范圍內(nèi)線性相關(guān)性較低；熱力學(xué)模型所確定的分形維數(shù)在整體孔徑尺度范圍內(nèi)均能有效地定量表征鹽堿土孔隙的分形特征，且與lgQn的線性相關(guān)系數(shù)較高。綜上所述，在評(píng)價(jià)該區(qū)域鹽堿土孔隙結(jié)構(gòu)的復(fù)雜程度時(shí)，應(yīng)用熱力學(xué)模型的效果是最好的。

4 結(jié)論

（1）孔軸線模型所得的鹽堿土孔隙結(jié)構(gòu)的分形維數(shù)在1.9260～2.1499 之間，且隨深度的增加，其分形維數(shù)呈先增加后減少的趨勢(shì)。0～30 cm 范圍內(nèi)，孔隙的迂曲程度逐漸變大，30～60 cm 范圍內(nèi)，孔隙的迂曲程度逐漸降低。鹽堿土的滲透系數(shù)在4.35～10.15 mm/h 之間，孔軸線模型所確定的分形維數(shù)與土壤滲透系數(shù)之間呈現(xiàn)較好的負(fù)相關(guān)性。

（2）采用4 種體積分形模型計(jì)算孔隙體積分形維數(shù)，空間填充模型不能應(yīng)用于定量表征鹽堿土孔隙的分形特征；毛細(xì)管壓力法模型在不同孔徑尺度范圍內(nèi)存在不同的分形維數(shù)，但在整體孔徑尺度范圍內(nèi)所體現(xiàn)出的分形維數(shù)在一定程度上也能定量表征孔隙的分形特征；當(dāng)孔徑在7 nm～10 μm 區(qū)間內(nèi)時(shí)，Menger 海綿模型能定量表征鹽堿土孔隙的分形特征，而當(dāng)孔徑d>10 μm 時(shí)，Menger 海綿模型無(wú)法得到合理的分形維數(shù)；熱力學(xué)模型所確定的分形維數(shù)在整體孔徑尺度范圍內(nèi)能有效表征孔隙的分形特征。通過(guò)比較4 種體積分形維數(shù)可知，熱力學(xué)模型能較好地定量表征該區(qū)域鹽堿土孔隙結(jié)構(gòu)的分形特征。