面向多因素影響的混合預(yù)測(cè)模型
謝 宇,王麗清,徐永躍,姚寒冰
(云南大學(xué) 信息學(xué)院,云南 昆明 650091)
0 引 言
在短時(shí)交通流的預(yù)測(cè)研究方面,為了取得更精確的預(yù)測(cè)結(jié)果,有的采用在時(shí)間序列歷史數(shù)據(jù)上建立自回歸模型AR、移動(dòng)平均模型MA,以及基于其上的各種組合和變形時(shí)間序列模型[1,2]的方法。也有采用基于相空間重構(gòu)[3]、自適應(yīng)遺傳粒子群優(yōu)化—加權(quán)最小二乘支持向量機(jī)[4]、K近鄰[5]、神經(jīng)網(wǎng)絡(luò)[6,7],以及深度學(xué)習(xí)的方法[8,9]等智能預(yù)測(cè)方法。其中,智能預(yù)測(cè)方法可更好地描述交通流中的非線性、不確定性,但又帶來(lái)大量數(shù)據(jù)獲取困難,數(shù)據(jù)去噪、清洗復(fù)雜,模型預(yù)測(cè)失效、算法效率低、計(jì)算性能不高等方面的問(wèn)題。
另一方面,交通流的影響因素復(fù)雜而多樣,只基于單一因素、特征和模型預(yù)測(cè),往往難以描述其它復(fù)雜外部環(huán)境因素或突發(fā)情況的影響,導(dǎo)致預(yù)測(cè)結(jié)果與現(xiàn)實(shí)情況的誤差增大。
因此,有了混合多種模型進(jìn)行預(yù)測(cè)的方法[10-12]。例如:Huang等提出了基于支持向量回歸模型與高斯損失函數(shù)的短期交通流量預(yù)測(cè)方法[13]。也有采用建立基于K近鄰的交通擁堵指數(shù)預(yù)測(cè)模型,以適應(yīng)天氣、節(jié)假日、重大活動(dòng)對(duì)交通擁堵帶來(lái)的影響[14]。或者在交通指數(shù)歷史基礎(chǔ)數(shù)據(jù)的基礎(chǔ)上,對(duì)引入天氣和工作日進(jìn)行回歸分析完成短時(shí)交通指數(shù)的預(yù)測(cè)[15]。為解決交通流的時(shí)空特征,用卷積神經(jīng)網(wǎng)絡(luò)CNN進(jìn)行交通流特征提取,繼而結(jié)合向量回歸分類器SVR進(jìn)行流量預(yù)測(cè)[16]。通過(guò)采集每周同一天的交通流數(shù)據(jù),結(jié)合BP神經(jīng)網(wǎng)絡(luò)和灰色預(yù)測(cè)模型,通過(guò)加權(quán)來(lái)作為最終預(yù)測(cè)值等[17]。這些方法,都一定程度結(jié)合了多種方法或模型,以適應(yīng)更復(fù)雜的現(xiàn)實(shí)情況的變化。但一方面是數(shù)據(jù)獲取困難,所蘊(yùn)含的數(shù)據(jù)相關(guān)性具有復(fù)雜的非線性,另一方面,對(duì)于外部因素,更多地從天氣、節(jié)假日等進(jìn)行考慮,而缺乏基于交管部門特有數(shù)據(jù)的預(yù)測(cè)分析。
為了實(shí)現(xiàn)對(duì)主道路和關(guān)鍵卡口,更準(zhǔn)確的未來(lái)短時(shí)路況預(yù)測(cè),本文結(jié)合差分自回歸移動(dòng)平均模型ARIMA與CART模型樹,基于所采集的道路卡口視頻實(shí)時(shí)數(shù)據(jù)、歷史流量數(shù)據(jù),并引入同時(shí)段卡口道路管控系統(tǒng)中的突發(fā)事故事件數(shù)據(jù)、天氣數(shù)據(jù)、節(jié)假日/工作日數(shù)據(jù),提出并實(shí)現(xiàn)了一個(gè)對(duì)多影響因素敏感的道路車流混合預(yù)測(cè)模型。
1 時(shí)間序列預(yù)測(cè)模型
1.1 基本思路和方法
車流量具有高度非線性和不穩(wěn)定性,導(dǎo)致使用數(shù)學(xué)統(tǒng)計(jì)模型,難以獲得精確的結(jié)果。機(jī)器學(xué)習(xí)模型中,人工神經(jīng)網(wǎng)絡(luò)可以準(zhǔn)確模擬復(fù)雜的非線性系統(tǒng),但可解釋性不佳,計(jì)算速度較慢。
對(duì)于由于多種可能的不可控因素發(fā)生,所導(dǎo)致的車流預(yù)測(cè)準(zhǔn)確度不高的問(wèn)題,本文采用結(jié)合ARIMA和CART決策樹的方法,構(gòu)建混合預(yù)測(cè)模型,在歷史車流數(shù)據(jù)基礎(chǔ)上,把天氣、節(jié)假日、突發(fā)事件發(fā)生等因素量化后,也作為預(yù)測(cè)模型的輸入?yún)?shù),使車流的預(yù)測(cè)在具有較快計(jì)算速度的同時(shí),也能更好地適應(yīng)其它多種外部因素帶來(lái)的影響,以嘗試解決面對(duì)突發(fā)情況車流預(yù)測(cè)問(wèn)題。
1.2 差分自回歸移動(dòng)平均模型ARIMA[17]
差分自回歸移動(dòng)平均模型ARIMA的實(shí)現(xiàn)原理是對(duì)非平穩(wěn)的時(shí)間序列,通過(guò)若干次差分使其成為平穩(wěn)序列,以獲得精度較高的預(yù)測(cè)結(jié)果。自回歸差分移動(dòng)平均模型(ARIMA(p,d,q))通常適用于長(zhǎng)期趨勢(shì)明顯的序列,其建模的前提是時(shí)間序列的平穩(wěn)性。如果不平穩(wěn),解決方法是采用預(yù)處理獲得平穩(wěn)序列,對(duì)平穩(wěn)序列得出預(yù)測(cè)結(jié)果,再做逆操作以取得最終預(yù)測(cè)結(jié)果。
ARIMA的建模過(guò)程如圖1所示。
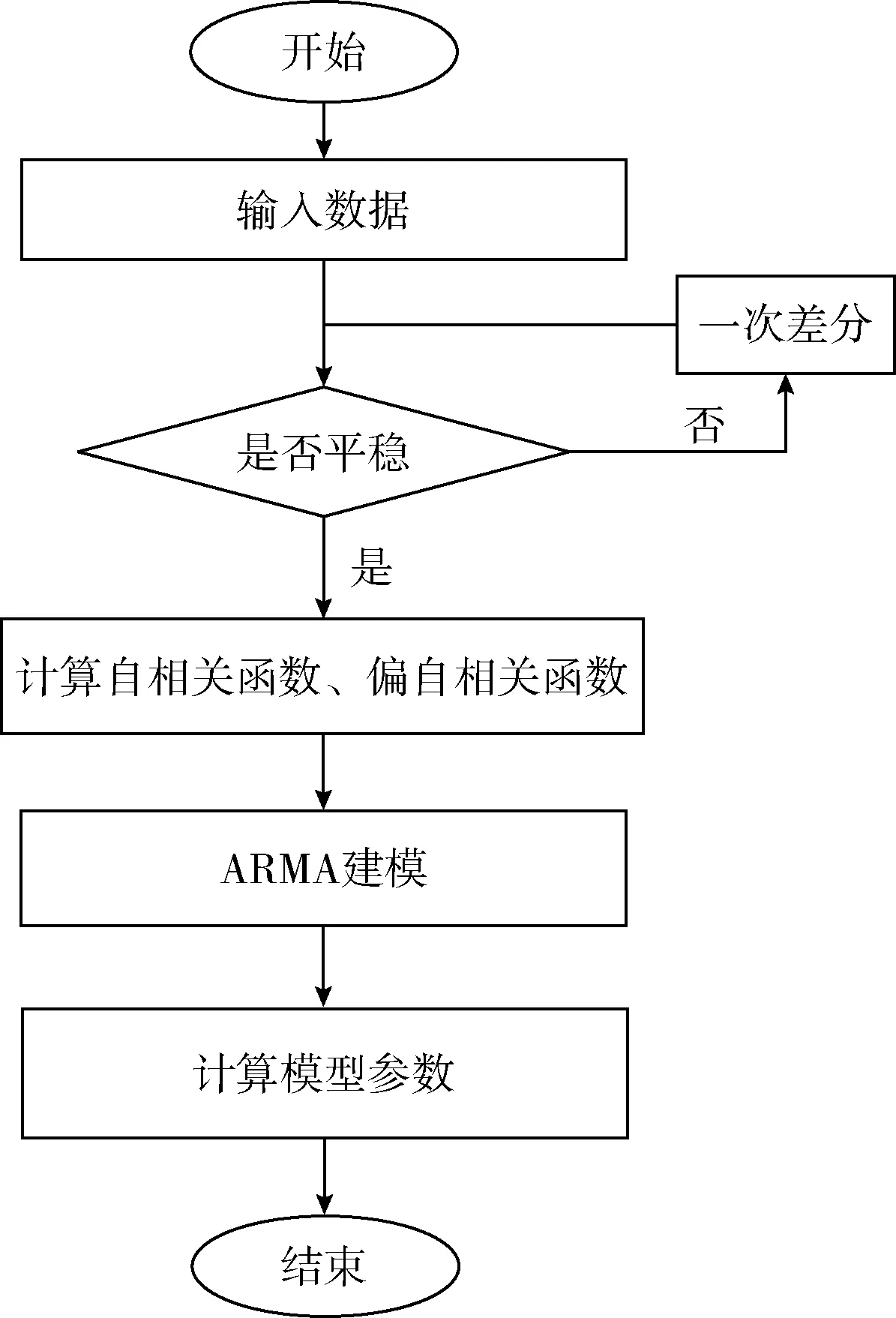
圖1 ARIMA建模過(guò)程
對(duì)數(shù)據(jù)平穩(wěn)性的檢測(cè)大多采用單位根檢驗(yàn)法ADF。檢驗(yàn)后,假設(shè)存在這樣的單位根,那么這段時(shí)間序列就是非平穩(wěn)的,需要通過(guò)參數(shù)d進(jìn)行差分處理,處理后再次判斷其平穩(wěn)性[18]。這樣,將ARIMA(p,d,q)模型轉(zhuǎn)化為ARMA(p,q)模型,用于后面建模[19]。
通過(guò)計(jì)算自相關(guān)函數(shù)(ACF)和偏自相關(guān)函數(shù)(PACF)可以確定模型的p、q參數(shù)值。判別時(shí)根據(jù)表1完成。
拖尾即k大于p后在0附近波動(dòng),但不會(huì)恒等于0。出現(xiàn)截尾,則是在大于k后值快速趨近于0。因此,從表1中看出, PACF和ACF中,同時(shí)出現(xiàn)拖尾,就可在確定參數(shù)p、q的情況下,用ARMA模型完成建模[20]。

表1 不同模型與ACF和PACF的關(guān)系
根據(jù)表1可以根據(jù)ACF圖和PACF圖的具體情況選用的模型確定時(shí)間序列模型數(shù)后,用最小二乘法完成參數(shù)計(jì)算。
1.3 分類回歸樹CART算法
分類回歸樹CART(classification and regression tree)是由Leo Breiman等提出用于分類或回歸的算法,也是數(shù)據(jù)挖掘領(lǐng)域內(nèi)的常用算法之一。其本質(zhì)是對(duì)特征空間的二元?jiǎng)澐郑瓤梢杂糜趧?chuàng)建分類樹,也可以用于創(chuàng)建回歸樹、模型樹,因而被廣泛應(yīng)用。
構(gòu)建時(shí),首先才用二分法完成切分,然后遍歷數(shù)據(jù)集中的所有特征,選出最優(yōu)特征,作為數(shù)據(jù)集分割的判斷依據(jù)。因此,特征選擇和剪枝是CART的關(guān)鍵。在特征選擇時(shí)可采用Gini系數(shù)完成判斷。
Gini系數(shù)可以用來(lái)度量數(shù)據(jù)的雜亂度,若數(shù)據(jù)集樣本的系數(shù)值越大,則不確定性越大,雜亂度越高,即選為特征。其計(jì)算公式如式(1)[21]所示
(1)
其中,D表示數(shù)據(jù)集全體樣本,n為樣本總數(shù),pi表示每種樣本出現(xiàn)的概率
ΔGini(X)=Gini(D)-GiniX(D)
(2)
在進(jìn)行特征選擇時(shí),用式(2)計(jì)算以特征X劃分后,數(shù)據(jù)不純度減小的程度,取值最大的X,可得到最優(yōu)切分。
CART算法核心除了特征選擇外,剪枝是算法的另一個(gè)關(guān)鍵步驟。CART使用代價(jià)復(fù)雜度剪枝算法。剪枝時(shí)使用的損失函數(shù)為式(3)
Cα(T)=C(T)+α|T|
(3)
其中,T為任意子樹,C(T)為預(yù)測(cè)的誤差,|T|為葉子節(jié)點(diǎn)總數(shù)。α用于衡量擬合程度和復(fù)雜度。
剪枝中,當(dāng)α從0逐漸增大到達(dá)某個(gè)閾值α1時(shí),可找到使損失函數(shù)值Cα1(T1)最小的子樹T1,存入列表L。然后,再增大α到某個(gè)閾值αp時(shí),找到使損失函數(shù)值Cαp(Tp)最小的子樹Tp,以此類推,直到α足夠大到子樹T成為根節(jié)點(diǎn),此時(shí)從存儲(chǔ)子樹的列表L中通過(guò)交叉驗(yàn)證選出最優(yōu)子樹,完成剪枝[22]。
本文采用CART模型樹將多屬性因素融入車流量的預(yù)測(cè),構(gòu)造車流預(yù)測(cè)混合模型。由于模型樹有分段線性建模的優(yōu)勢(shì),其每個(gè)葉節(jié)點(diǎn)包含一個(gè)線性方程,并且模型樹的葉子節(jié)點(diǎn)除線性方程外,也可以是其它的機(jī)器學(xué)習(xí)模型。也因此,模型樹的采用使得本混合預(yù)測(cè)模型擁有了更強(qiáng)的適應(yīng)性和更高的預(yù)測(cè)準(zhǔn)確度。
2 多因素混合預(yù)測(cè)模型構(gòu)建
2.1 設(shè)計(jì)思想
混合預(yù)測(cè)模型的基本思想是:在基于歷史車流量的預(yù)測(cè)數(shù)據(jù)基礎(chǔ)上,用模型樹引入更多的外在影響因素參與最終的預(yù)測(cè),提高預(yù)測(cè)結(jié)果對(duì)多種外部影響因素的敏感性,提高預(yù)測(cè)結(jié)果的準(zhǔn)確度[22]。
多因素混合預(yù)測(cè)模型的框架如圖2所示。
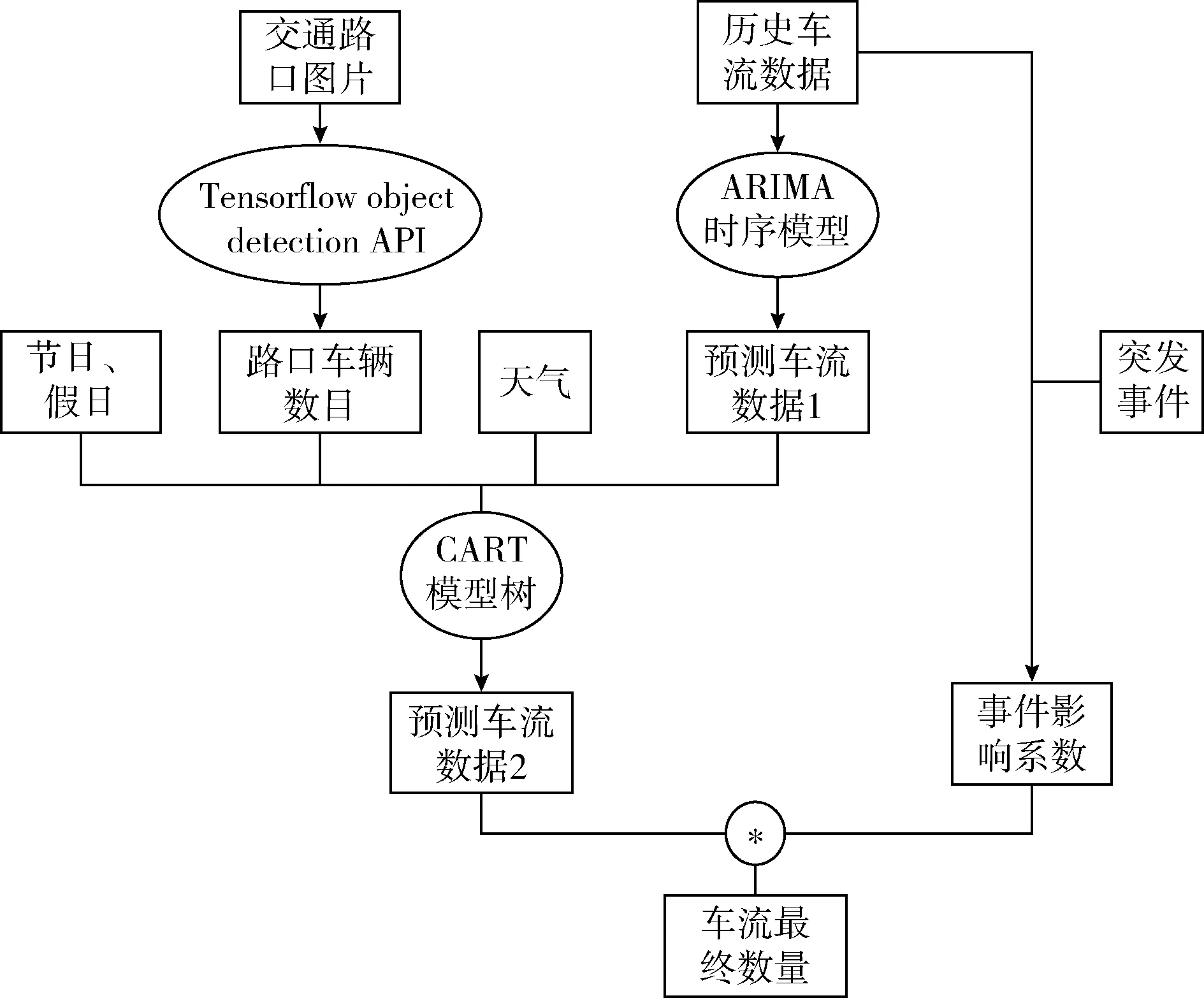
圖2 混合模型框架設(shè)計(jì)
(1)基于ARIMA生成預(yù)測(cè)車流數(shù)據(jù)1
使用自回歸時(shí)序模型ARIMA,基于從交管部門采集得到的歷史車流數(shù)據(jù),進(jìn)行序列擬合,預(yù)測(cè)并生成未來(lái)時(shí)間的車流量預(yù)測(cè)數(shù)據(jù)1。
(2)引入其它多因素影響因子
這些影響因子包括路口實(shí)時(shí)車流、天氣、節(jié)假日、突發(fā)事件。具體描述如下:
1)路口車輛檢測(cè)
基于交管局在城市道路口安置的攝像頭實(shí)時(shí)抓拍的圖片,采用TensorFlow object detection API進(jìn)行圖片中車輛數(shù)目的自動(dòng)檢測(cè)(對(duì)于設(shè)置有流量監(jiān)測(cè)的路口直接引入實(shí)時(shí)流量監(jiān)測(cè)數(shù)據(jù))。綜合平衡網(wǎng)絡(luò)、性能和結(jié)果準(zhǔn)確性,采取30 s一次的間隔,拍攝5次,得到的數(shù)量總和作為下步預(yù)測(cè)的其中一個(gè)影響因子。
2)天氣數(shù)據(jù)
通過(guò)互聯(lián)網(wǎng)提供的公共天氣預(yù)報(bào)數(shù)據(jù),獲取未來(lái)一段時(shí)間的天氣特征,并根據(jù)天氣晴朗到惡劣程度按數(shù)值范圍10~50進(jìn)行量化。
3)雙休和節(jié)假日
雙休和節(jié)假日信息通過(guò)查詢?nèi)諝v,計(jì)算出雙休、調(diào)休和節(jié)假日的具體日期,按工作日、周末雙休、法定節(jié)假日將日期特征分為3類,分別按數(shù)值10~50范圍完成量化。
4)事件影響系數(shù)
事件影響系數(shù)用于表示事件對(duì)車流的影響程度,默認(rèn)為1,表示沒(méi)有特殊事件發(fā)生;當(dāng)發(fā)生事件時(shí),基于歷史車流數(shù)據(jù),將事件發(fā)生時(shí)間段的車流量均值,與日常時(shí)間段車流量均值相比,作為該事件的影響系數(shù)。
該數(shù)據(jù)來(lái)源于交管部門系統(tǒng)記錄的特殊突發(fā)事件,包括事故、施工等。
(3)基于CART模型樹和事件影響系數(shù)得出最終預(yù)測(cè)結(jié)果
使用CART模型樹,將預(yù)測(cè)數(shù)據(jù)1與所得到的所有外部影響數(shù)據(jù)通過(guò)決策樹與回歸方程進(jìn)行融合,輸出第二次預(yù)測(cè)的車流量值,該二次預(yù)測(cè)結(jié)果值即是考慮了多種復(fù)雜影響因子的最終預(yù)測(cè)結(jié)果。
2.2 混合模型預(yù)測(cè)方法和實(shí)現(xiàn)
根據(jù)模型設(shè)計(jì)思想框架圖,預(yù)測(cè)的實(shí)現(xiàn)步驟如下[22]:
(1)從交管部門所采集的車流數(shù)據(jù)中,將24小時(shí)數(shù)據(jù)以15 min為單位,切分為96個(gè)時(shí)間點(diǎn),得到某段時(shí)間的車流量時(shí)間序列,記為
T[i]=[time[i],RealData[i]]
其中,time[i]為時(shí)間點(diǎn),RealData[i]為對(duì)應(yīng)的time[i]時(shí)刻的實(shí)際車流量,i為序號(hào);
(2)將T[i]中的time[i]與RealData[i]作為自回歸時(shí)序模型ARIMA的輸入,預(yù)測(cè)的得到Δt內(nèi)的車流量數(shù)據(jù)Predict1[i],加入到T[i]序列中,得到
T[i]=[time[i],RealData[i],Predict1[i]]
(3)交通道路監(jiān)控?cái)z像頭拍攝的抓拍圖片進(jìn)行車輛檢測(cè),得到車輛數(shù)值,或根據(jù)提供的過(guò)車流量監(jiān)測(cè)數(shù)據(jù)得到變量CarNum[i];從天氣預(yù)報(bào)數(shù)據(jù)中提取需要預(yù)測(cè)的未來(lái)時(shí)間段Δt內(nèi)的天氣數(shù)據(jù),量化后得到Weather[i];按工作日、周末雙休日而非國(guó)家法定節(jié)假日、國(guó)家法定節(jié)假日進(jìn)行數(shù)據(jù)量化后得到Holiday[i];
依次把車流監(jiān)測(cè)數(shù)據(jù)CarNum[i]、天氣Weather[i]、節(jié)假日數(shù)據(jù)Holiday[i]加入T[i]中,得到
T[i]=[time[i],RealData[i],Predict1[i],CarNum[i],
Weather[i],Holiday[i]]
(4)基于以上步驟得到的數(shù)據(jù)集T[i],將其中的特征變量Predict1[i],CarNum[i],Weather[i],Holiday[i]作為自變量,RealData[i]作為因變量,輸入到CART算法模型樹中。樣本數(shù)據(jù)見(jiàn)表2,訓(xùn)練得到模型樹每個(gè)葉子節(jié)點(diǎn)的回歸方程參數(shù),回歸方程如下
Predict2[i]=A0+A1×Predict1[i]+A2×
CarNum[i]+A3×Weather[i]+A4×Holiday[i]
使用得到的模型樹進(jìn)行預(yù)測(cè),得到二次預(yù)測(cè)值Predict2[i];
(5)檢索交管部門系統(tǒng)中的事故、路段施工等事件信息,對(duì)事件影響范圍內(nèi)的關(guān)聯(lián)路口,提取預(yù)先計(jì)算設(shè)定的對(duì)應(yīng)事件影響系數(shù),將步驟(4)得到的二次預(yù)測(cè)值Predict2[i]乘以該事件影響系數(shù),再作為最終預(yù)測(cè)的車流量數(shù)值。
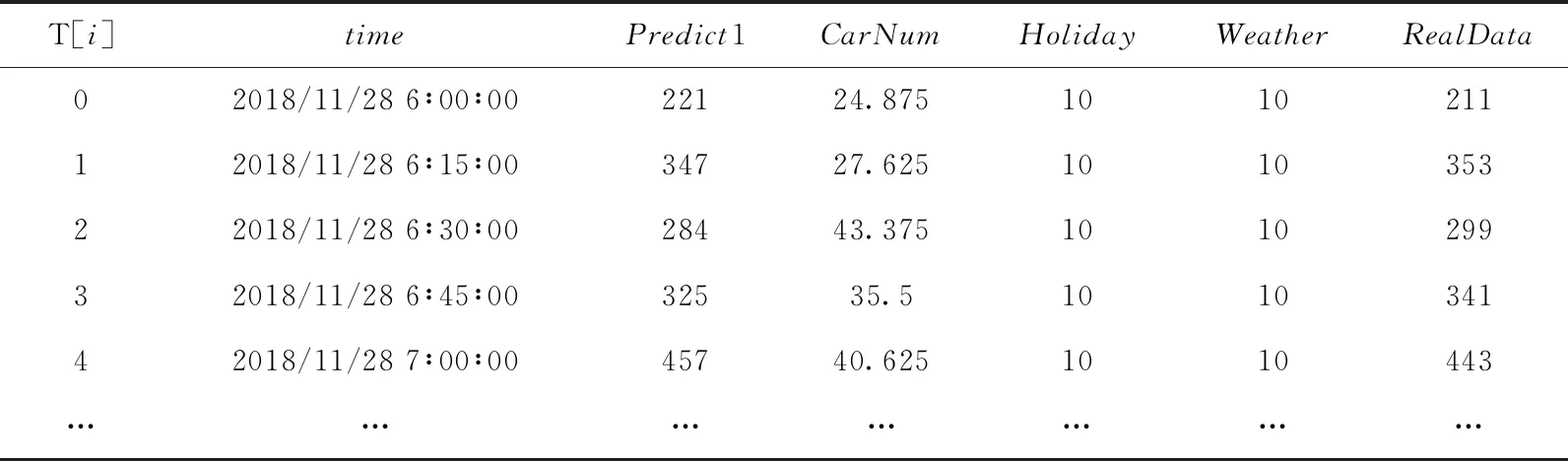
表2 實(shí)驗(yàn)樣本部分?jǐn)?shù)據(jù)
3 實(shí)驗(yàn)評(píng)估和結(jié)果分析
3.1 實(shí)驗(yàn)數(shù)據(jù)
為了驗(yàn)證多因素混合預(yù)測(cè)模型預(yù)測(cè)效果,采用的實(shí)驗(yàn)數(shù)據(jù)為:時(shí)間區(qū)間2018年9月至2019年1月,該時(shí)間段內(nèi)多因素特征包括:日常工作日、突降暴雨天氣(2018-11-28)、元旦節(jié)假日、圍擋事件發(fā)生時(shí)段(2018-12-18)的典型路段過(guò)車流量監(jiān)測(cè)數(shù)據(jù)和視頻圖像數(shù)據(jù)(圖3~圖5),共約280萬(wàn)條過(guò)車數(shù)據(jù)。
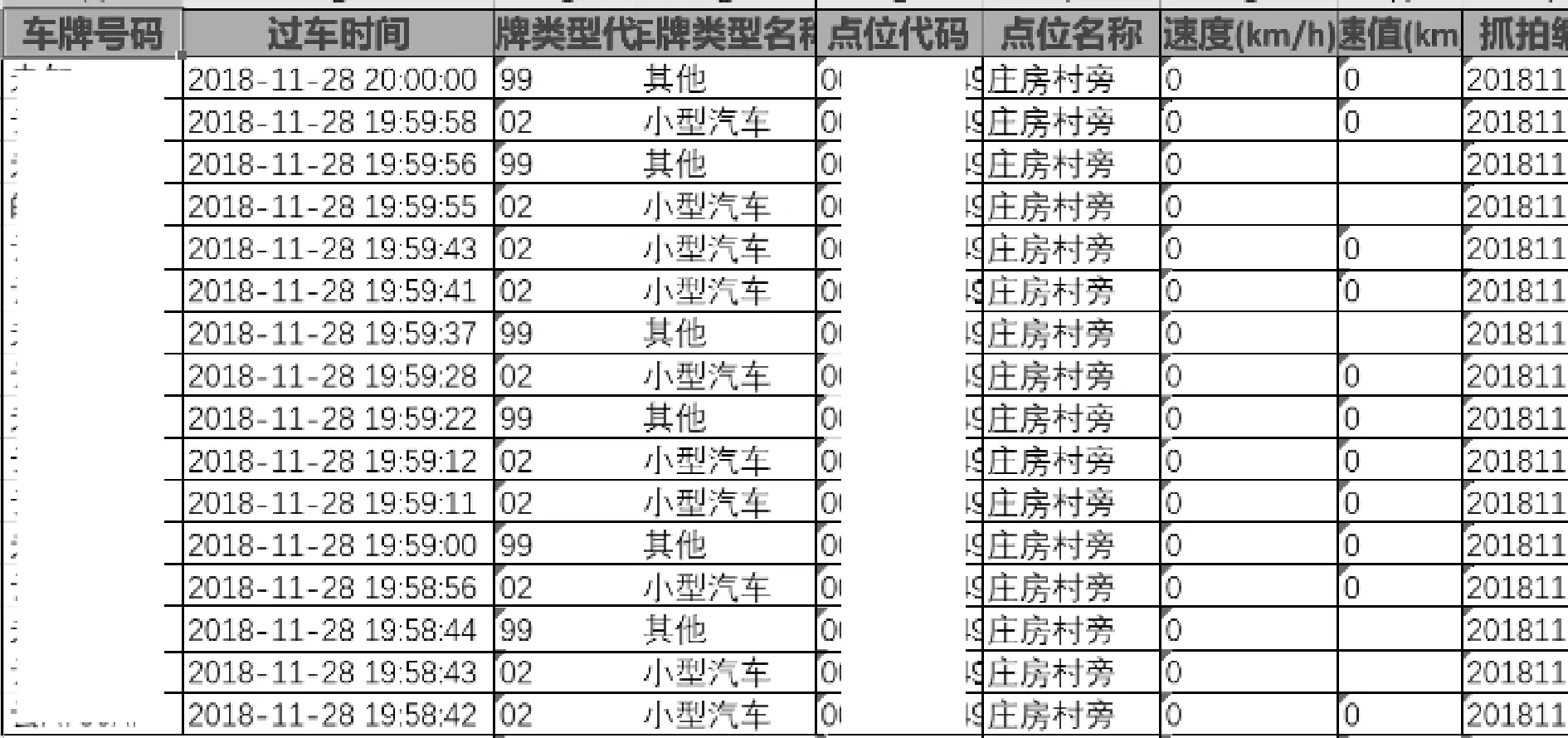
圖3 天氣變化突降暴雨時(shí)道路部分過(guò)車數(shù)據(jù)
圖4 元旦時(shí)道路部分過(guò)車信息
圖5 突發(fā)事件發(fā)生部分圍擋時(shí)道路部分過(guò)車數(shù)據(jù)
3.2 評(píng)估分析方法
為了評(píng)估本文混合模型的最終效果,采用均方根誤差RMSE(root mean square error)作為評(píng)價(jià)指標(biāo),對(duì)比分析模型預(yù)測(cè)結(jié)果與實(shí)際值之間的偏差。均方根誤差計(jì)算公式如下
3.3 實(shí)驗(yàn)結(jié)果分析
為了驗(yàn)證模型的不同預(yù)測(cè)效果,基于所提供的真實(shí)測(cè)試數(shù)據(jù),分別對(duì)一般工作日、突降暴雨、元旦節(jié)假日、圍擋事件發(fā)生時(shí)間段的車流預(yù)測(cè)進(jìn)行了對(duì)比,并結(jié)合預(yù)測(cè)結(jié)果圖和誤差,對(duì)ARIMA模型與本文的多因素混合模型的預(yù)測(cè)結(jié)果進(jìn)行了比較和分析。
實(shí)驗(yàn)結(jié)果如下:比較如圖6和圖7可知:兩種模型在工作日突降暴雨的情況下,模型預(yù)測(cè)結(jié)果與真實(shí)車流數(shù)據(jù)曲線之間,具有較好的一致性,預(yù)測(cè)結(jié)果接近于真實(shí)值。
比較如圖8和圖9可知:在元旦法定節(jié)假日時(shí)段,兩種模型所得到的車流預(yù)測(cè)曲線,與真實(shí)車流曲線之重合度較高。
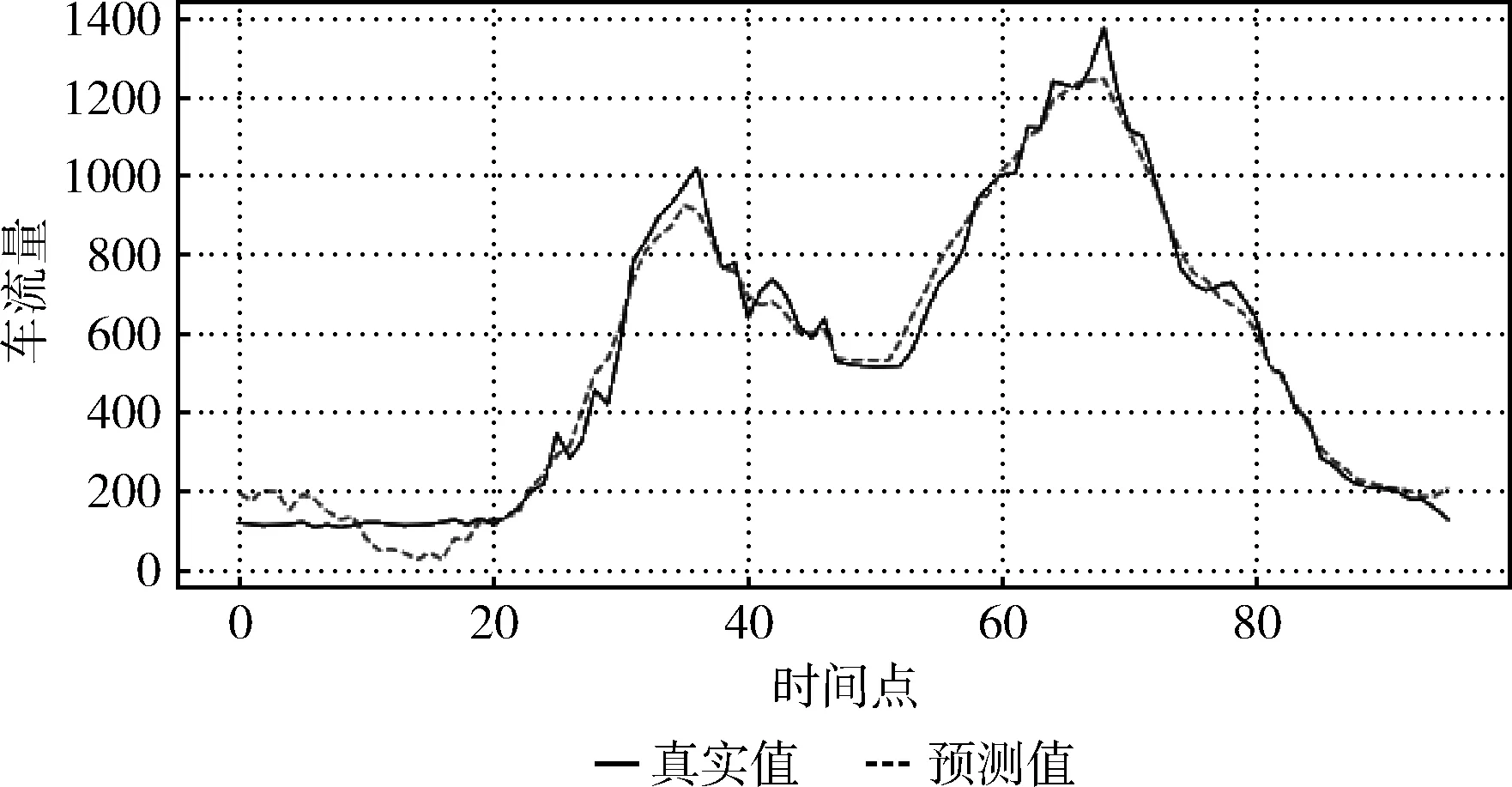
圖6 工作日時(shí)段ARIMA模型預(yù)測(cè)車流數(shù)據(jù)與真實(shí)數(shù)據(jù)對(duì)比
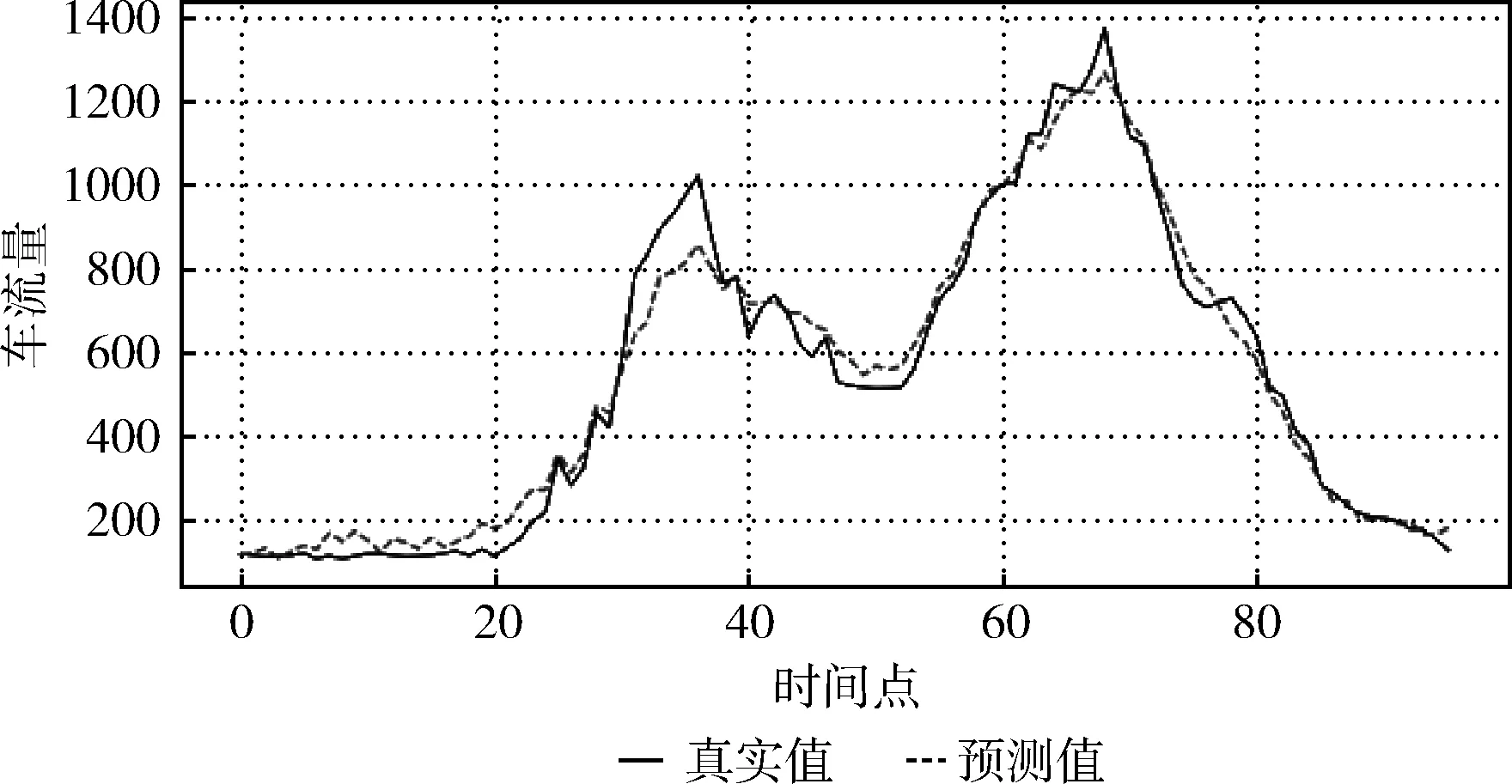
圖7 工作日時(shí)段混合模型預(yù)測(cè)車流數(shù)據(jù)與真實(shí)數(shù)據(jù)對(duì)比

圖8 元旦時(shí)段ARIMA模型預(yù)測(cè)車流數(shù)據(jù)與真實(shí)數(shù)據(jù)對(duì)比
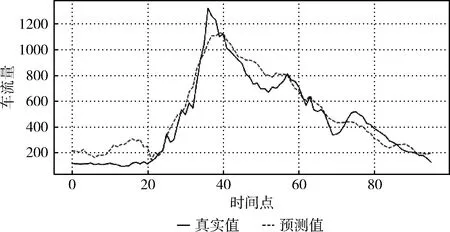
圖9 元旦時(shí)段混合模型預(yù)測(cè)車流數(shù)據(jù)與真實(shí)數(shù)據(jù)對(duì)比
在橫坐標(biāo)為35的位置存在車流量的波峰,相對(duì)來(lái)說(shuō),混合模型的預(yù)測(cè)結(jié)果比ARIMA模型預(yù)測(cè)結(jié)果更接近真實(shí)車流值。但在橫坐標(biāo)小于20和大于40的區(qū)間,混合模型預(yù)測(cè)的結(jié)果相對(duì)來(lái)說(shuō)抖動(dòng)較大,而ARIMA模型預(yù)測(cè)的結(jié)果較為平滑。分析原因是在節(jié)假日的因子量化中采用了經(jīng)驗(yàn)值估計(jì)的方法,帶來(lái)一定誤差影響。
比較如圖10、圖11可知:在道路圍擋施工等事件發(fā)生時(shí),由于事件的突發(fā)性,ARIMA模型預(yù)測(cè)曲線保留了沒(méi)有事件發(fā)生時(shí)段的車流量走勢(shì),因此誤差較大。而混合模型預(yù)測(cè)車流曲線,由于在結(jié)果中引入了突發(fā)事件影響因子,因此預(yù)測(cè)結(jié)果明顯更接近于真實(shí)車流曲線。
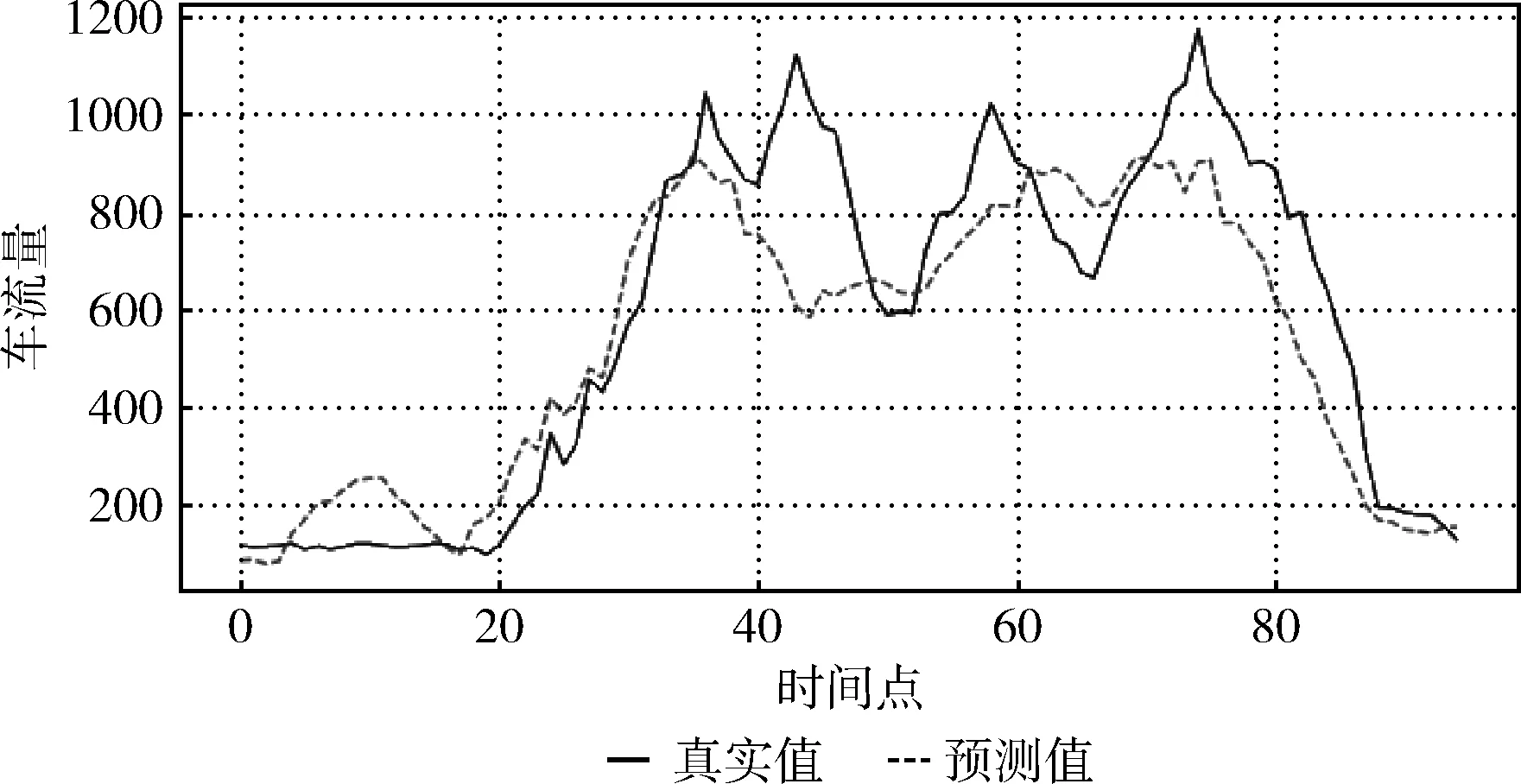
圖10 道路施工時(shí)段ARIMA模型預(yù)測(cè)車流數(shù)據(jù)與真實(shí)數(shù)據(jù)對(duì)比
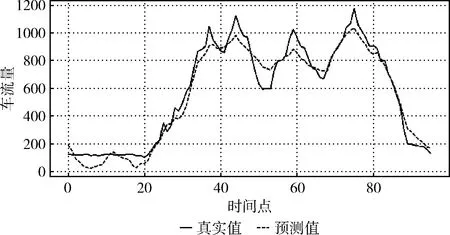
圖11 道路施工時(shí)段混合模型預(yù)測(cè)車流數(shù)據(jù)與真實(shí)數(shù)據(jù)對(duì)比
對(duì)兩種模型預(yù)測(cè)值的在3種狀態(tài)下的誤差對(duì)比分析見(jiàn)表3。
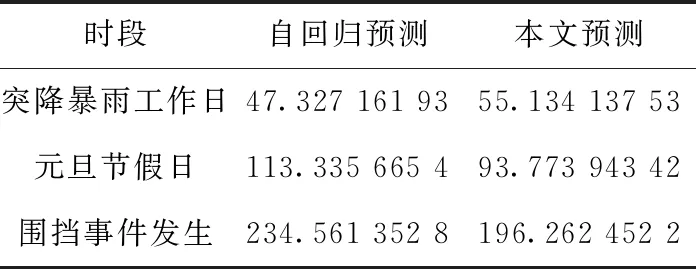
表3 均方根誤差對(duì)比
從上述實(shí)驗(yàn)結(jié)果可知,在工作日天氣突變情況下,兩種方法的預(yù)測(cè)結(jié)果差異不大(圖6和圖7),ARIMA模型與混合預(yù)測(cè)模型的預(yù)測(cè)效果接近,混合預(yù)測(cè)值較平緩,對(duì)于天氣影響的敏感反應(yīng)方面不明顯,分析原因應(yīng)該是對(duì)于工作日出行天氣不是主要影響因素,天氣原因造成道路封閉或交通中斷事件發(fā)生更可能引起車流的顯著變化。
在元旦等節(jié)假日,混合模型預(yù)測(cè)值在車流高峰時(shí)比ARIMA預(yù)測(cè)值更接近真實(shí)值,但抖動(dòng)較大。
在圍擋特殊事件發(fā)生時(shí),混合模型預(yù)測(cè)值由于引入影響因子,比ARIMA預(yù)測(cè)結(jié)果誤差小,預(yù)測(cè)更準(zhǔn)確。
總的來(lái)說(shuō),ARIMA模型的預(yù)測(cè)依據(jù)是預(yù)測(cè)時(shí)間之前時(shí)間段的車流趨勢(shì),忽略了事件帶來(lái)的影響,而混合模型在時(shí)序模型的基礎(chǔ)上,加入了各種因素的變化影響,基于模型樹葉子回歸方程再次對(duì)預(yù)測(cè)數(shù)據(jù)進(jìn)行計(jì)算和修正,降低了均方根誤差,使得預(yù)測(cè)結(jié)果更貼近于真實(shí)值。
4 結(jié)束語(yǔ)
本文提出的基于ARIMA和CART模型樹的混合預(yù)測(cè)模型,在時(shí)序預(yù)測(cè)結(jié)果數(shù)據(jù)上,通過(guò)模型樹將天氣變化、節(jié)假日、突發(fā)事件等復(fù)雜環(huán)境中的多重影響因素量化后,引入到預(yù)測(cè)模型,使預(yù)測(cè)結(jié)果更能適應(yīng)復(fù)雜、多變的外部環(huán)境帶來(lái)車流規(guī)律變化大的情況。
研究成果將有助于交管部門充分挖掘和應(yīng)用所掌握的數(shù)據(jù),依托先進(jìn)信息技術(shù)方法,開(kāi)展道路交通管理科研,輔助交管部門進(jìn)行科學(xué)決策,增強(qiáng)對(duì)道路的交通協(xié)調(diào)與控制能力,提高道路通行效率。
根據(jù)研究和實(shí)驗(yàn)驗(yàn)證,從預(yù)測(cè)結(jié)果比較圖和均方根誤差分析,混合預(yù)測(cè)模型與ARIMA模型相比,混合預(yù)測(cè)模型在節(jié)假日或者突發(fā)偶發(fā)事件中,可以獲得更好的預(yù)測(cè)結(jié)果。
但是,由于在研究中采用了組合模型,數(shù)值傳遞次數(shù)的增加可能導(dǎo)致數(shù)據(jù)計(jì)算偏差累積,此外也帶來(lái)了計(jì)算復(fù)雜性的提升。下步的研究一方面是對(duì)影響因子的量化和算法做進(jìn)一步的改進(jìn)和優(yōu)化,另一方面將增加對(duì)傳入數(shù)據(jù)的優(yōu)化處理環(huán)節(jié),以進(jìn)一步提高預(yù)測(cè)準(zhǔn)確性。

