船模阻力CFD結果的不確定度分析
張立,周傳明,陳偉民,陳建挺
(上海船舶運輸科學研究所 航運技術與安全國家重點實驗室,上海 200135)
CFD技術是船舶水動力領域的關鍵技術之一,是船舶性能評估、線型優化等方面的重要且高效的工具[1]。CFD方法雖然高效,但是其計算效率和精度受到使用人員的經驗、計算模型設置等因素的影響,甚至在某些情況下出現較大誤差[2-3]。因此,針對CFD計算精度的分析就顯得十分必要。
關于CFD不確定度分析,早期的研究大多是基于網格收斂性的CFD不確定度分析,如針對特定湍流模型和特定壁面條件下,對結構化網格或非結構化網格的數值模擬過程進行不確定度分析[4-6];使用不同的湍流方法對船模CFD計算結果進行驗證和確認[7],來比較不同湍流模型之間的不確定度分析的差異;有部分研究通過方差分析的方式對CFD數值模擬進行不確定度分析[8-9],此方法所依賴的前提是數值模擬結果隨著因素變化呈現正態分布趨勢,但是這種前提并未得到驗證。因此,CFD不確定度的分析方法仍然處于探討階段,一套統一的分析方法并未建立。近期的研究趨向通過提升分析因素的維度來比較CFD不確定度分析之間的差異,如不同船型、不同尺度、不同湍流模型及不同壁面條件等維度。
針對CFD計算結果在不同壁面條件(Y+)下的不確定度差異問題,考慮基于1艘模型長度為7.455 2 m的標準船模,基于k-ε湍流模型,設置不同壁面條件(Y+=60、120、240),并分別設置3套不同密度的網格尺寸,對其進行船模阻力CFD模擬,在前序進行多維度仿真的基礎上,參考ITTC關于CFD模擬的不確定度規程,對數值模擬結果進行不確定度分析,即驗證和確認(V&V)。
1 原理
1.1 CFD計算方法
CFD湍流模型分為DNS、LES、RANS等。RANS方法通過簡化N-S方程,控制方程和連續性方程如下式所示。該方法降低了計算難度,也提升了計算速度,深受工業界青睞。

(i,j=1、2、3)
(1)
在計算船模阻力時,將速度進口、壓力出口、自由液面、船體壁面等作為邊界條件。
1.2 分析要素的選擇
基于RANS方法的湍流模型有很多變體,不同的湍流模型具有不同的適用性,在求解數值結果時,湍流模型的選擇對結果產生重要影響。網格密度對計算結果收斂性有明顯影響。離散格式主要對計算效率造成影響,但對結果精度的影響十分有限。在近壁面處的流動,由于是從黏性底層到湍流的轉化,需要壁面函數處理。RANS方法通過壁面函數控制近壁面處流動問題,通過壁面函數結合湍流模型求解計算域,通過引入無量綱數值Y+進行控制。對于時間步長,當設置的時間步長滿足相應的庫朗數要求之后,近似認為時間步長對結果的影響可以消除。根據文獻[8],除了湍流模型外,船模阻力仿真結果主要受網格密度、近壁面處理的影響,因此,本文針對不同近壁面條件,設置不同網格密度分析其不確定度。
2 CFD不確定度分析方法
對于數值模擬結果S和真值T之間的誤差δS,可以分為模型誤差δM和數值誤差δN,見圖1。

圖1 CFD模擬的誤差示意
其中,模型誤差是對物理問題進行描述時候帶來的誤差,數值誤差是因為數值求解過程中因數學方程求解帶來的誤差[10]。因此,CFD數值模擬時需要分別進行分析,分析過程分為2個步驟(V&V):①驗證,評估數值結果的不確定度;②確認,評估數值結果的正確性。通常意義上的V&V是一個分析過程,這與船模試驗不確定度分析有所不同。
2.1 驗證
當對船模阻力進行CFD模擬,其數值結果因不同的湍流模型、網格密度、近壁面條件、時間步長及其他因素等多種因素影響。因此,當湍流模型和Y+一定的時候,CFD模擬的不確定度表示為
(2)
式中:UI、UG、UP分別為迭代誤差、網格收斂性、以及其他因素的不確定度。
迭代誤差是由于每個計算步驟中的當前解與精確解之間的誤差造成的,截斷誤差主要是因為數值求解過程中高階項的舍入造成的。
對于迭代誤差,當計算結果是取一段較長時間的均值,且計算結果為單調收斂的趨勢,則該項誤差為小量,迭代誤差可按照收斂結果上下界之半(yU-yL)/2來計算。其中yU、yL分別為計算收斂結果的上下限。
按照三角分布計算,迭代誤差不確定度為
(3)
目前的CFD不確定度分析方法中,截斷誤差根據網格收斂性進行分析,通過定義統一的網格增長比,劃分多套網格,分析其收斂性,然后通過外推法對結果進行估計[11]。
因此,通過上文的分析,便可以對數值模擬的結果進行驗證。
2.2 確認
對數值模擬的結果進行確認的過程,也是將數值結果與試驗結果和真值進行比較的過程。確認是利用基準試驗數據評估數值模擬的模型不確定度UM的過程。試驗結果D和數值模擬S之間的誤差即為比較誤差E,即
E=D-S
(4)
其中,試驗結果D帶有測量不確定度,S取值SGF,即為細化網格的數值模擬結果。
數值模擬結果S包含模型誤差δM和數值誤差δN,即
E=D-S=δD-(δM+δN)
(5)
數值模擬結果的確認過程的不確定度UV為
(6)
式中:UD為試驗結果的不確定度;UN為驗證過程中的數值不確定度。
通過式(4)~(6),便可以比較UV和E的結果是否得到確認。當UV>|E|,則UV在該層次得到確認;如果UV?|E|,則表明數值結果偏離試驗值較遠,需要改進計算模型。
3 標準船模阻力結果分析
針對標準船模的CFD阻力結果進行不確定度分析,通過湍流模型、網格密度和Y+3個方面對數值結果進行驗證,同時結合所進行的試驗結果對CFD不確定度進行確認。
在湍流模型選擇上,選擇標準k-ε湍流模型;網格劃分方面,使用三維非結構網格,網格總數的加細比約為rG=2;Y+值的增速rY+=2,見表1。
3.1 計算模型
船模主尺度,船模速度及相關參數見表2。

表1 CFD不確定度分析計算設置

表2 船模主尺度
3.2 驗證
通過設計計算矩陣,對船模阻力進行CFD模擬,半船計算結果見表3。

表3 標準k-ε湍流模型的計算結果
3.2.1 驗證方法
此前的計算結果中,與常規的CFD不確定度分析不同:選擇2個維度上的分析,需要分別進行驗證。收斂因子RG為
(7)
式中:SGF、SGM、SGC分別表示細網格、中網格和粗網格的結果。當0 (8) 誤差修正因子CG為 (9) 根據ITTC(2017)建議,當誤差修正因子CG<1時, UG=[2|1-CG|+1]·δRE (10) 當CG遠小于或者遠大于1時,網格的不確定度為 UG=[|CG|+|1-CG|]·δRE (11) 3.2.2 數值不確定度 根據式(2)計算得到驗證過程中的不確定度UV,見表4。 表4 不同Y+值計算結果的數值不確定度 對相同條件的船模進行拖曳水池試驗,總阻力測量結果RT=22.789×(1±0.32%),其中0.32%為試驗結果的不確定度。在得到數值不確定度之后,確認過程的不確定度UV見表5。 表5 確認過程的不確定度 表5表明,當Y+=60時,由于UV 如圖2所示,整體而言,本文數值模擬結果的誤差在3%以內,與其他相關文獻相比,本文的數值模擬結果具有較高精度。但是,Y+=60的結果并未得到確認,而Y+=120和240的結果得到了驗證和確認。從不確定度分析的角度上,Y+=60的分析過程應當使用更多套的網格進一步分析,同時也說明當Y+值選擇不合適的時候,即使對網格進行加密并不一定能獲得收斂結果或高精度結果。因此,在進行數值模擬時,Y+值要與湍流模型相匹配。 圖2 k-ε計算結果誤差 1)Y+值對不確定度分析結果產生了明顯影響,即使采用相同的網格收斂驗證方案,不同Y+值時的不確定度分析結果不相同。 2)從本文的數值模擬結果發現,Y+值對數值模擬的結果影響比網格密度的影響更大;針對k-ε湍流模型,并非Y+值選擇越小,計算結果精度便越高。需經過多次校驗,合理設置計算模型才能夠提高計算結果的精度。 3)通過比較結果,使用多套網格增加網格收斂性的驗證,能夠提升計算結果的可信程度。

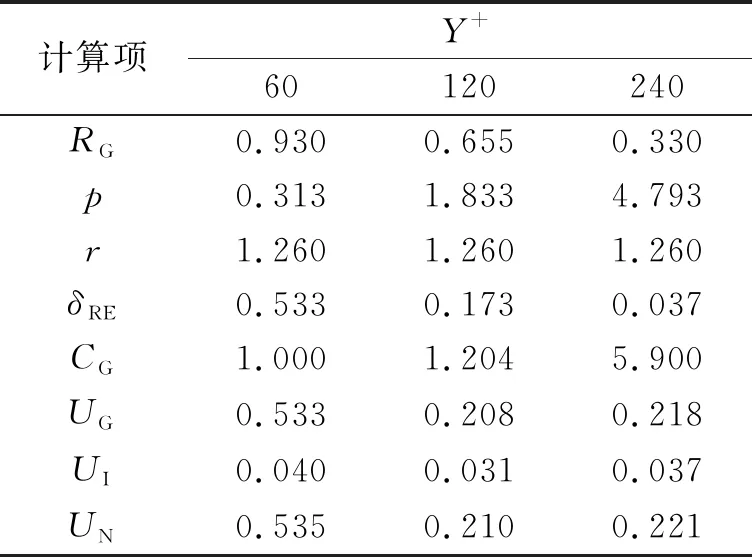
3.3 確認
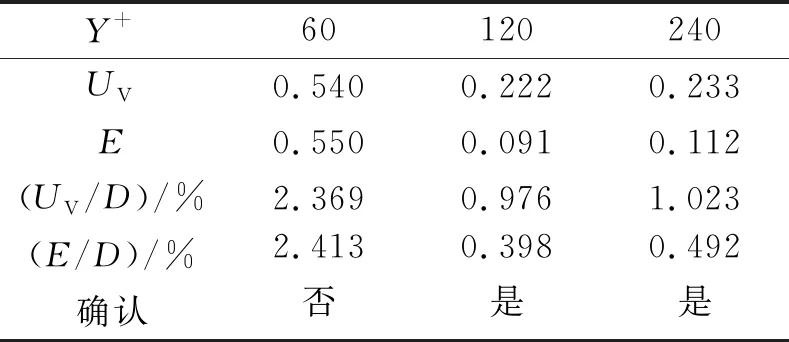
3.4 改進數值模擬的方法

4 結論

