LCL型并網逆變器并聯諧振機理分析及抑制方法

陶海軍， 周猶松， 張國澎， 鄭 征

(河南理工大學 電氣工程與自動化學院， 河南 焦作 454000)

近年來，隨著能源和環境問題的日益突出，可再生能源的并網發電技術得到了越來越多的關注.其中，并網逆變器是風能、光伏發電等分布式發電系統的核心組成部分，因此受到了廣泛的關注[1-2].相較于L型濾波器，LCL型濾波器對高頻諧波抑制能力強，具有體積小、成本低等優勢，目前被廣泛應用于各類并網設備中[3].在實際應用中，單個LCL型并網逆變器并網運行時能滿足并網要求[4-5].然而，多個LCL型并網逆變器同時并聯運行時，系統會發生諧振和不穩定的現象.多個并網逆變器并聯運行的諧振問題已經影響了新能源并網發電技術的大規模推廣及應用[6-7].因此，對于多個并網逆變器并網諧振原理及其諧振抑制策略的研究具有重要意義.

針對多個并網逆變器并聯系統存在諧振的問題，國內外學者展開了多方面的研究.文獻[8]提出針對1種多個并網逆變器系統的建模和控制方法，指出n個并網逆變器并聯運行時，系統中單臺并網逆變器的等效電網阻抗可等效為實際電網阻抗的n倍.文獻[9-11]分析了電網阻抗對多個并網逆變器系統LCL諧振特性的影響，這些方法雖然分析了多并網逆變器并聯系統的諧振機理，但并未考慮并網逆變器之間交互作用，未對其影響進行分析.為討論并網逆變器之間以及并網逆變器與電網之間的交互作用，文獻[12]提出了1種基于等效電網阻抗的直觀分析方法，對系統的諧振頻率特性和穩定性進行了分析.文獻[13]討論了在弱電網情況下的交互作用，提出了交互電流和公共電流的概念，并對系統穩定性分為交互穩定性和公共穩定性進行分析.在文獻[12-13]的基礎上，文獻[14]揭示了由交互電流產生的諧振現象，并分析了逆變器之間交互諧振對系統諧振和動態特性產生的影響.但文獻[12-14]中假設所有并網逆變器參數、控制策略及控制參數均相同，而在實際應用場合中，由于并網容量、輸出電流以及LCL濾波器參數等不同，直接影響多逆變器并聯系統諧振頻率和諧振尖峰的個數，增加了對多逆變器并聯系統諧振特性分析的難度[15].因此，涉及不同容量逆變器并聯系統的文獻較少.

為深入研究多并網逆變器并聯系統的諧振機理，本文以兩臺并網逆變器并網系統為例，利用疊加定理分析了各逆變器對并網電流的影響，對并網電流進行分解，對比分析了相同和不同容量并網逆變器并聯系統的諧振頻率點特性.基于多逆變器并聯系統中由交互電流產生的諧振頻率點，設計了數字陷波器，引入到傳統電容電流反饋有源阻尼控制中，實現了此類系統對多諧振頻率點的抑制，滿足了系統的并網要求.最后，在MATLAB/Simulink仿真平臺中搭建了相同和不同額定容量逆變器并聯系統仿真模型，驗證了所提策略對于弱電網下多并網逆變器并聯運行的可行性.

1 兩逆變器并聯系統結構與控制模型

兩臺逆變器并聯拓撲結構如圖1所示，每組逆變單元分別通過LCL濾波器接入并網公共點(PCC)，經電網阻抗與電網連接.圖中：Udcn為逆變器n的直流側電壓(n=1,2)；Z1n、ZCn、Z2n為逆變器n的逆變器側電感感抗、濾波電容容抗及網側電感感抗；U0n為逆變器n的逆變橋輸出電壓；Zg為電網電感感抗；Ug為電網電壓；i2n為逆變器n并網輸出電流；ig為并網總電流.

(1)

式中：s為拉普拉斯變換因子；L1n為逆變器側電感；L2n為網側電感；Cn為濾波電感.

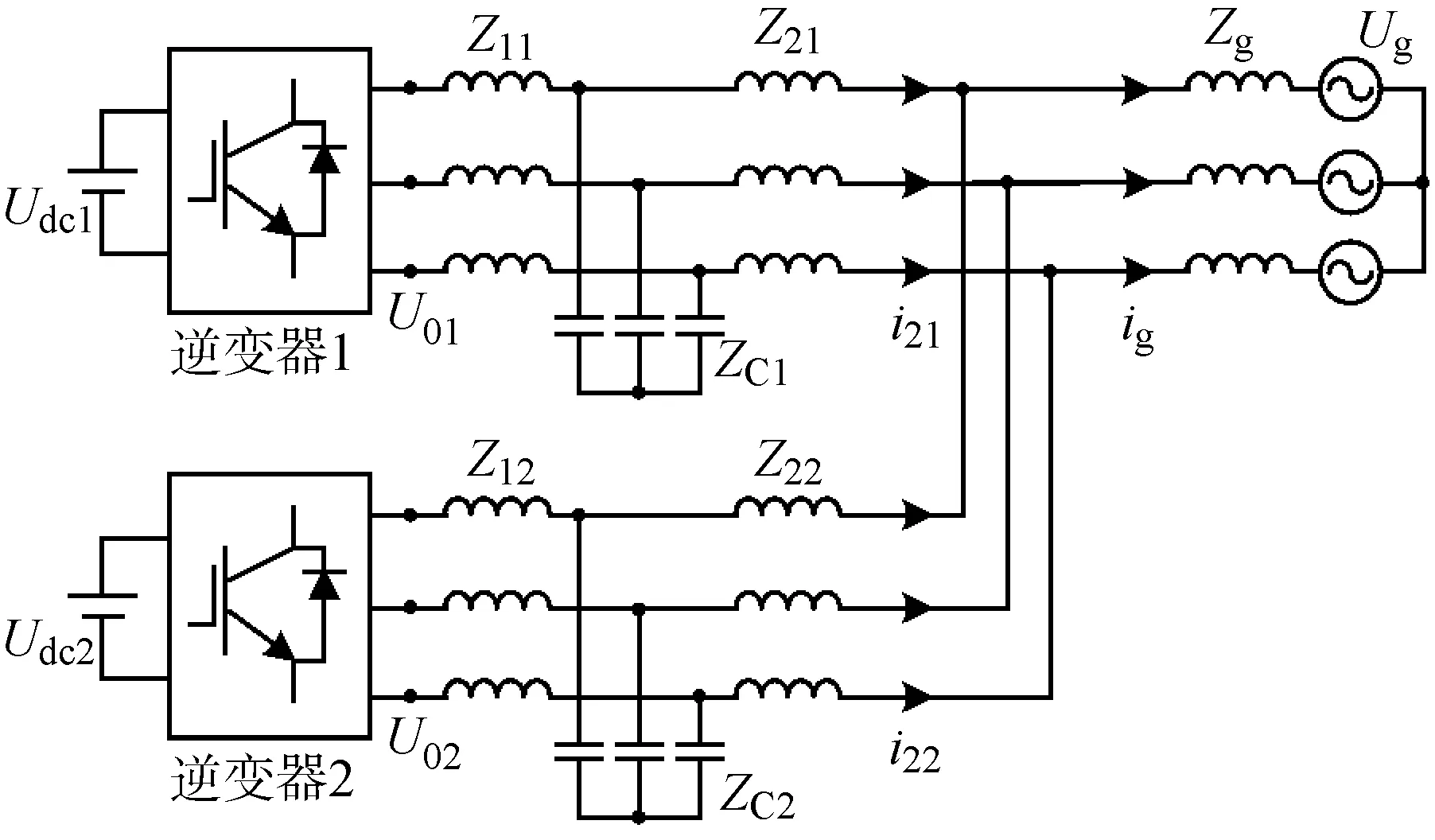
圖1 兩個并網逆變器并聯運行系統模型Fig.1 Parallel operation system model of two grid-connected inverters

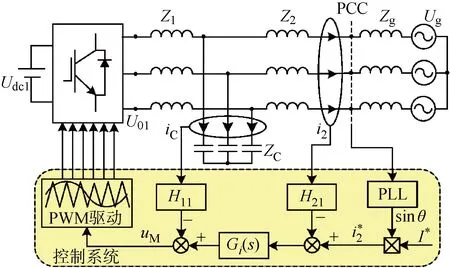
圖2 單個并網逆變器控制結構圖Fig.2 Control structure diagram of single grid-connected inverter

根據圖2可以推導出逆變器旋轉坐標系下電流環s域控制模型，如圖3所示.圖中：KPWM為uM到u01的傳遞函數.

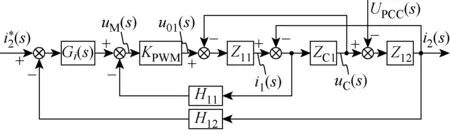
圖3 單個并網逆變器的電流環控制策略Fig.3 Current loop control strategy of single grid-connected inverter

2 兩逆變器并聯系統的建模與諧振分析

2.1 并聯系統的阻抗模型

對系統而言，Ug可視為擾動量，對LCL濾波器諧振尖峰的阻尼沒有影響.為便于分析兩逆變器之間的關系，可將U0n等效為電壓源[12]，則系統控制框圖可簡化為圖4(a).兩逆變器并聯系統是多輸入多輸出的系統，其中，U0n為輸入變量，i2n為輸出控制變量.由于逆變器1、2采用相同的電路結構和控制方式，本文以逆變器1的并網電流i21為例進行分析.由于2組逆變器是并聯運行，所以每組逆變橋輸出電壓U0n均會對i21產生影響.采用疊加原理對i21與U0n的關系進行分析.如圖4(b)所示，系統可以分為兩部分：一部分為逆變橋1自身輸出電壓U01對并網電流i21的作用；另一部分為逆變橋2輸出電壓U02對并網電流i21的影響.因此，對于1個多逆變器并聯系統，逆變器與逆變器之間存在交互作用.

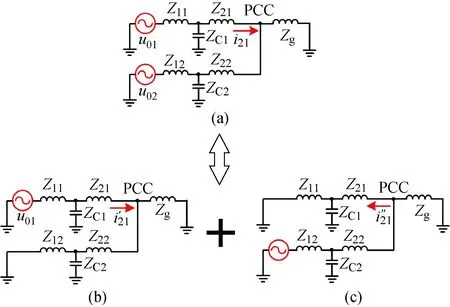
圖4 并聯逆變器疊加原理的等效電路圖Fig.4 Equivalent circuit diagram of parallel inverter superposition principle

由圖4(b)、4(c)可得U0n與i21之間的傳遞函數為

(2)

(3)

式中：參數M=Z11Z21+Z11ZC1+Z21ZC1；N=Z12ZL22+Z12ZC2+Z22ZC2；P=Z12+ZC2；Q=Z11+ZC1.Z11、Z21分別為逆變器1的逆變側電感電抗和網側電感電抗，Z12、Z22分別為逆變器2的逆變側電感電抗和網側電感電抗.

同理，可得U0n與i22之間的傳遞函數為

(4)

(5)

由于兩逆變器并聯系統是多輸入多輸出系統，則U0n與i2n之間的關系為

(6)

由式(2)～(6)可得：

(7)

則ig為

(8)

通過對比i2n和ig可知，逆變器n并網電流受到由逆變器1、2的共同作用，均由兩部分組成.一部分電流存在于逆變器之間，且不流入電網中，每組逆變器的電流大小相等，但方向相反，稱為交互電流，其表達式為

(9)

另一部分電流則流入電網中，每組逆變器的電流大小相等，且方向相同，稱為公共電流，其表達式為

(10)

系統中交互電流與公共電流的關系如圖5所示.

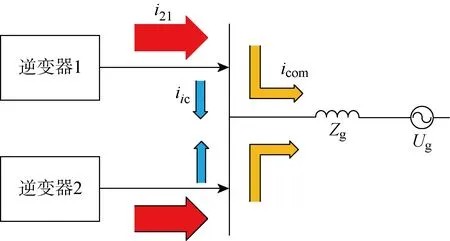
圖5 并聯系統的交互電流和公共電流Fig.5 Interactive current and common current for paralleled system

2.2 并聯系統的諧振分析

由式(9)可知u0n與iic的傳遞函數為

(11)

(12)

由式(10)可知u0n與icom的傳遞函數為

(13)

(14)

由式(13)、(14)可求得兩諧振頻率分別為

(15)

(16)

式中：

當采用相同容量逆變器并聯運行時，諧振頻率為

(17)

式中：Lg為電網阻抗.

圖6所示為采用相同額定容量逆變器并聯系統傳遞函數Gic、Gcom的幅頻特性圖.圖中：f為頻率；δ為相位；σ為幅值.由圖6和式(17)可以看出，交互電流的諧振僅受ωres，1的影響，該諧振點與LCL濾波器的參數有關，與LCL濾波器自身諧振頻率相同.而公共電流僅受到ωres，2的影響，該諧振頻率與LCL濾波器參數有關，也與Lg均有關.而n臺相同逆變器并網系統相當于每臺逆變器的電網總阻抗等效增大N倍[4]，此時系統諧振頻率ωr與公共電流諧振頻率ωres,2相同，即

(18)

圖6 相同額定容量并聯逆變器的幅頻特性Fig.6 Amplitude frequency characteristics of parallel inver-ters with the same rated capacity

圖7所示為采用不同額定容量逆變器并聯系統傳遞函數Gic、Gcom的幅頻特性圖.與相同額定容量逆變器并聯系統不同的是，采用不同容量逆變器并聯時，兩諧振點同時作用于交互電流、公共電流，且ωres,1和ωres,2均發生了偏移，兩諧振點的大小與每臺逆變器的LCL濾波器參數及Zg均相關.

單臺逆變器并聯系統時，逆變器只與電網阻抗之間存在交互作用，采用有源阻尼控制能夠有效抑制單個諧振尖峰；而多臺逆變器并聯系統中每組逆變器分別采用獨立并網控制，每組逆變器有源阻尼能對ωres,2起到抑制作用，但對于ωres,1未起到阻尼抑制.因此，傳統有源阻尼抑制并不適用于多逆變器并聯運行系統.

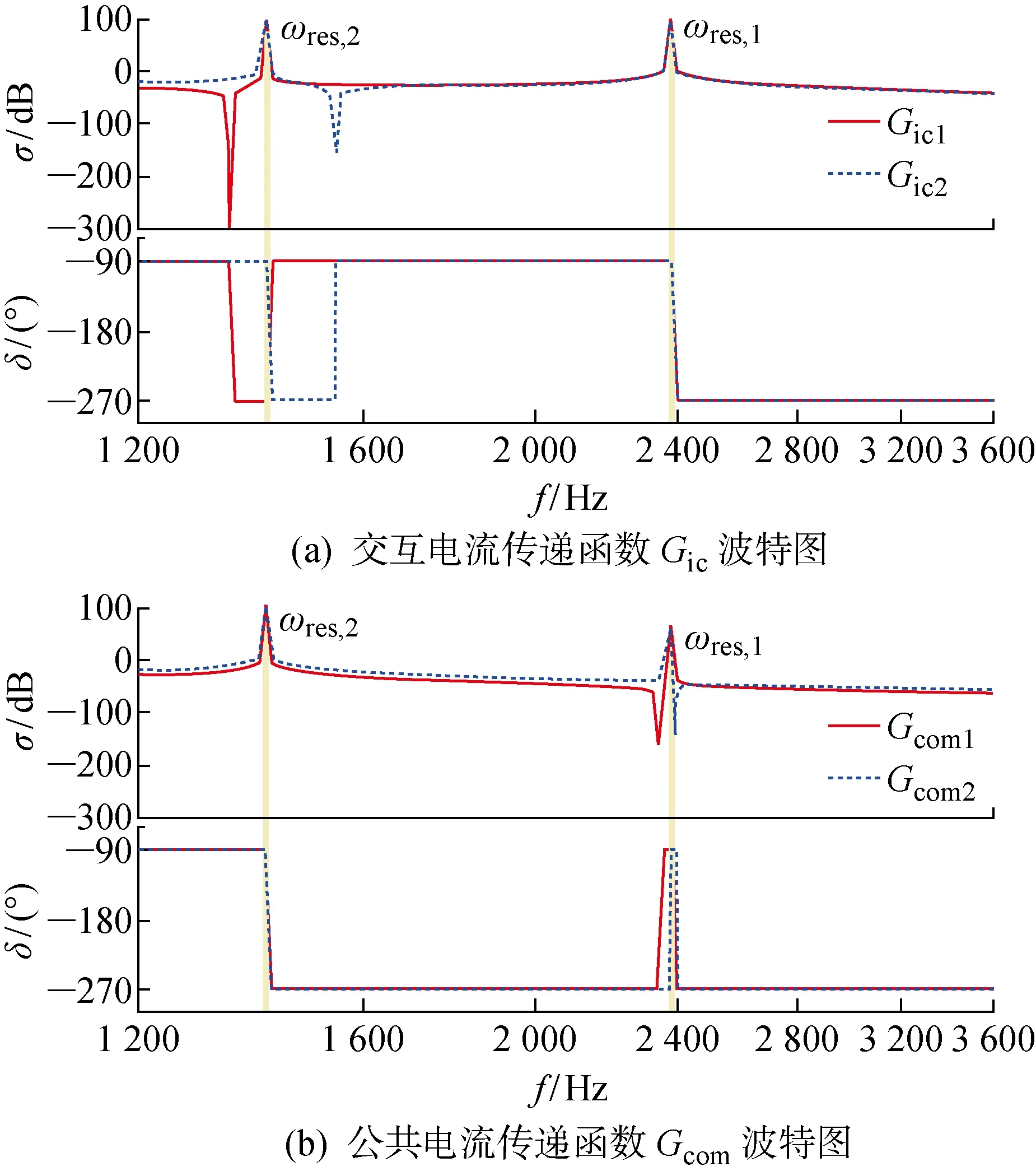
圖7 不同額定容量并聯逆變器的幅頻特性Fig.7 Amplitude frequency characteristics of parallel inverters with different rated capacities

3 并聯系統諧振抑制策略

3.1 改進的系統控制框圖

當單個并網逆變器并網時，采用傳統電容電流反饋有源阻尼方式能夠有效抑制由LCL濾波器和電網交互作用產生的單諧振尖峰；而當個多逆變器同時并聯運行時，由于逆變器之間交互諧振的存在，系統會出現諧振或不穩定的現象.

針對兩逆變器并聯系統的多諧振問題，本文采用基于數字陷波器的電容電流有源阻尼方法.圖8為改進的系統控制框圖.在電容電流有源阻尼抑制的基礎上，依據交互諧振點設計了相應的數字陷波器，引入電流環控制器，對系統中交互諧振進行抑制.當系統中公共諧振點發生輕微偏移時，電容電流反饋仍能實現對其阻尼抑制[16-17]；當陷波器的陷波頻率與交互諧振頻率相等時，數字陷波器會提供1個與交互頻率相反的反諧振尖峰來抵消系統的正諧振尖峰，而在其余頻段，數字陷波器阻尼的增益為0，不會影響其余頻段的幅頻特性.通過數字陷波器和電容電流反饋有源阻尼的共同作用，實現了此類系統中交互諧振和公共諧振的共同抑制.

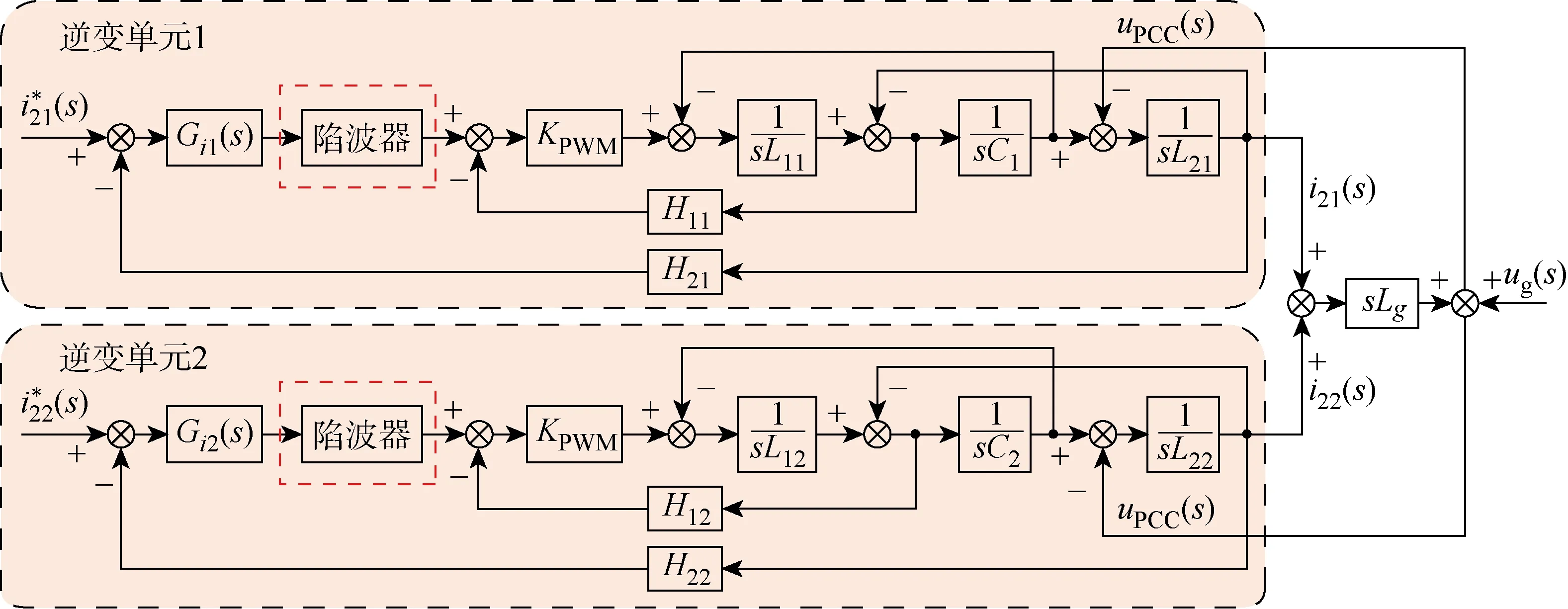
圖8 基于數字陷波器的電容電流反饋控制框圖Fig.8 Capacitance current feedback control block diagram based on digital notch

3.2 數字陷波器的設計

本文選取的數字陷波器為典型的二階陷波器，具有計算量小、頻率選擇性好的優點，其傳遞函數表達式為

(19)

式中：ωn為陷波器的中心角頻率，取值為ωres,1；ζ為阻尼系數，其取值的大小會影響到陷波器的抗擾動能力.為使系統能保持良好的穩定性和響應速度，ζ取值為工程上的最佳阻尼比0.707.

針對兩逆變器并聯系統，本文選取兩組不同容量的逆變器進行并聯為例進行說明，兩組逆變器的參數如表1和2所示.其中，三相全橋逆變器采用正弦脈寬調制(SPWM)控制，KPWM可近似表示為

KPWM=uM/2Utri

(20)

式中：Utri為三角載波的幅值.

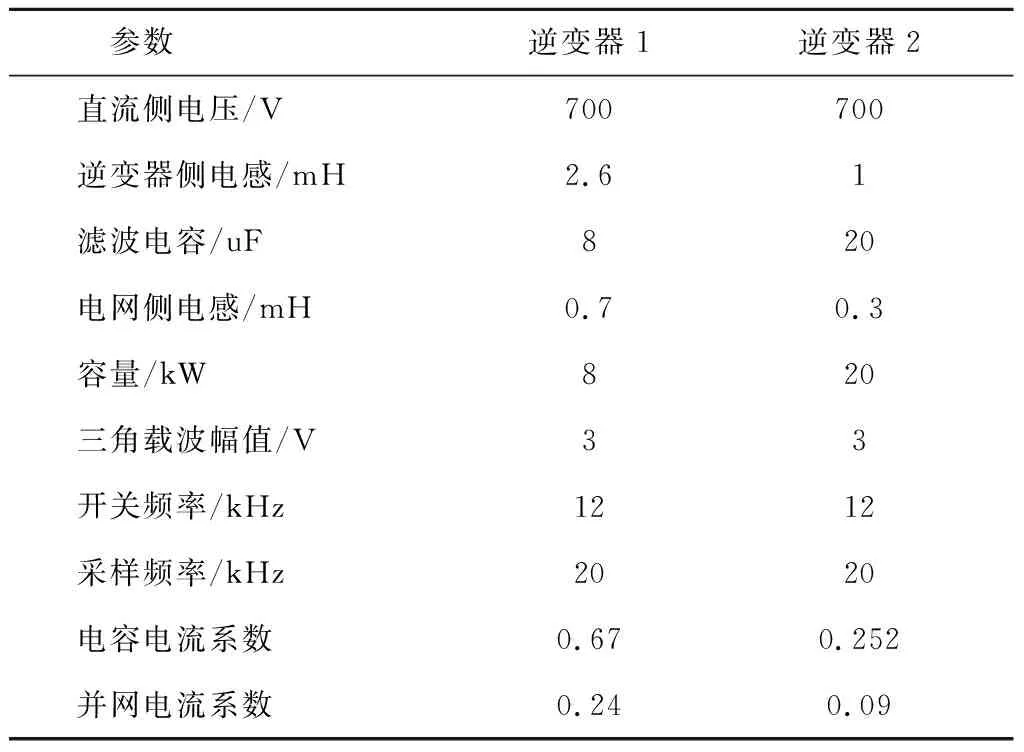
表1 并網逆變器主要參數Tab.1 Main parameters of grid-connected inverters

表2 電網參數Tab.2 Parameters of power grid

圖9 兩組8 kW逆變器并聯運行仿真結果Fig.9 Simulation results of parallel operation of two 8 kW inverters

當容量為8 kW的兩組相同逆變器并聯運行時，由式(13)可知，數字陷波器的諧振角頻率為ωn=ωres,1=15 055 rad/s.采樣時間T=1×10-4s，利用雙線性變化法對其進行離散化，陷波器的傳遞函數為

(21)

式中：z為變換因子.同理，容量為8 kW、20 kW兩組不同逆變器并聯運行時，數字陷波器的諧振角頻率為ωn=ωres,1=14 955 rad/s，陷波器的傳遞函數為

(22)

4 系統仿真

為了驗證本文提出的基于數字陷波器的電容電流有源阻尼方法的正確性和有效性，用MATLAB/Simulink建立了系統仿真模型.

4.1 兩相同容量并網逆變器并網運行

當采用容量為8 KW的兩組逆變器1并聯運行時，在時間t=0.2 s時由改進控制方式切換為傳統控制方式，圖9為i21、i22、ig和并網電壓UPCC波形.

由圖9可知：t<0.2 s時兩組并網逆變器均能實現穩定運行，此時兩組逆變器輸出電流的諧波總畸變率(THD)分別為1.51%、1.48%，并網總電流的THD為0.89%，且并網公共點PCC處電壓穩定；t=0.2 s時，控制方式由改進控制方式轉換為傳統控制方式，兩組逆變器輸出電流、并網總電流和并網公共點PCC處電壓均發生諧振，系統不穩定.因此，采用基于數字陷波器的電容電流反饋控制策略能夠消除交互電流引起的諧振，并網電流電能質量得到了明顯改善，有效降低了并網電流的總諧波畸變率.

圖10為兩組逆變器并聯運行時，在t=0.2 s時斷開第2組逆變器時的運行狀態對比圖.通過對比可知：t<0.2 s時，兩組并網逆變器均能實現穩定運行，并網電流均滿足并網要求，且并網公共點PCC處電壓穩定；而t=0.2 s時，當第2組逆變器離網時，第1組逆變器僅在切換時有輕微震蕩，第1組逆變器仍能穩定運行，此時并網電流的THD為0.99%.因此，當系統由兩臺逆變器并網運行切換為單臺逆變器并網運行時，并網電流在1個周期內能迅速達到穩定狀態，具有快速動態響應能力.

圖10 當逆變器2離網時仿真結果Fig.10 Simulation results when Inverter 2 is off grid

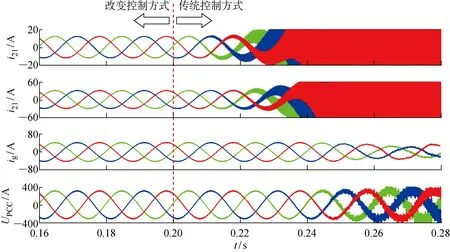
圖11 兩組不同容量逆變器并聯運行仿真結果Fig.11 Simulation results of parallel operation of two groups of inverters with different capacities

4.2 兩不同容量并網逆變器并網運行

當采用額定容量為8 KW的逆變器1和20 kW的逆變器2并聯運行時，兩逆變器的電流環控制方式在t=0.2 s時由改進方式切換為傳統方式，圖11為i21、i22、ig和UPCC波形.

由圖11可知：t<0.2 s時，兩組并網逆變器均能實現穩定運行，此時兩組逆變器輸出電流的THD分別為1.66%、1.03%，并網總電流的THD為0.88%，且并網公共點PCC處電壓穩定；而t=0.2 s時，控制方式由改進方式轉換為傳統方式時，兩組并網逆變器輸出電流、并網總電流和并網公共點PCC處電壓均發生諧振，系統不穩定.因此，采用基于數字陷波器的電容電流反饋控制策略對不同容量逆變器并聯系統也能實現良好的諧振抑制效果.

逆變器1和逆變器2并聯運行，t=0.2 s時切換為單逆變器并聯運行，圖12為各個逆變器輸出電流、并網總電流和并網電壓波形.通過對比可知：t<0.2 s時，兩組并網逆變器均能實現穩定運行，并網電流滿足并網要求，且并網公共點PCC處電壓穩定；而t=0.2 s時，當逆變器2離網時，逆變器1僅在切換時并網電流、并網電壓發生輕微震蕩，系統仍保持穩定運行狀態，此時并網電流的THD為1.02%.因此，當系統由兩臺不同額定容量逆變器并網運行切換為單臺逆變器并網運行時，并網電流在一個周期內能迅速達到穩定狀態，具有快速動態響應能力.

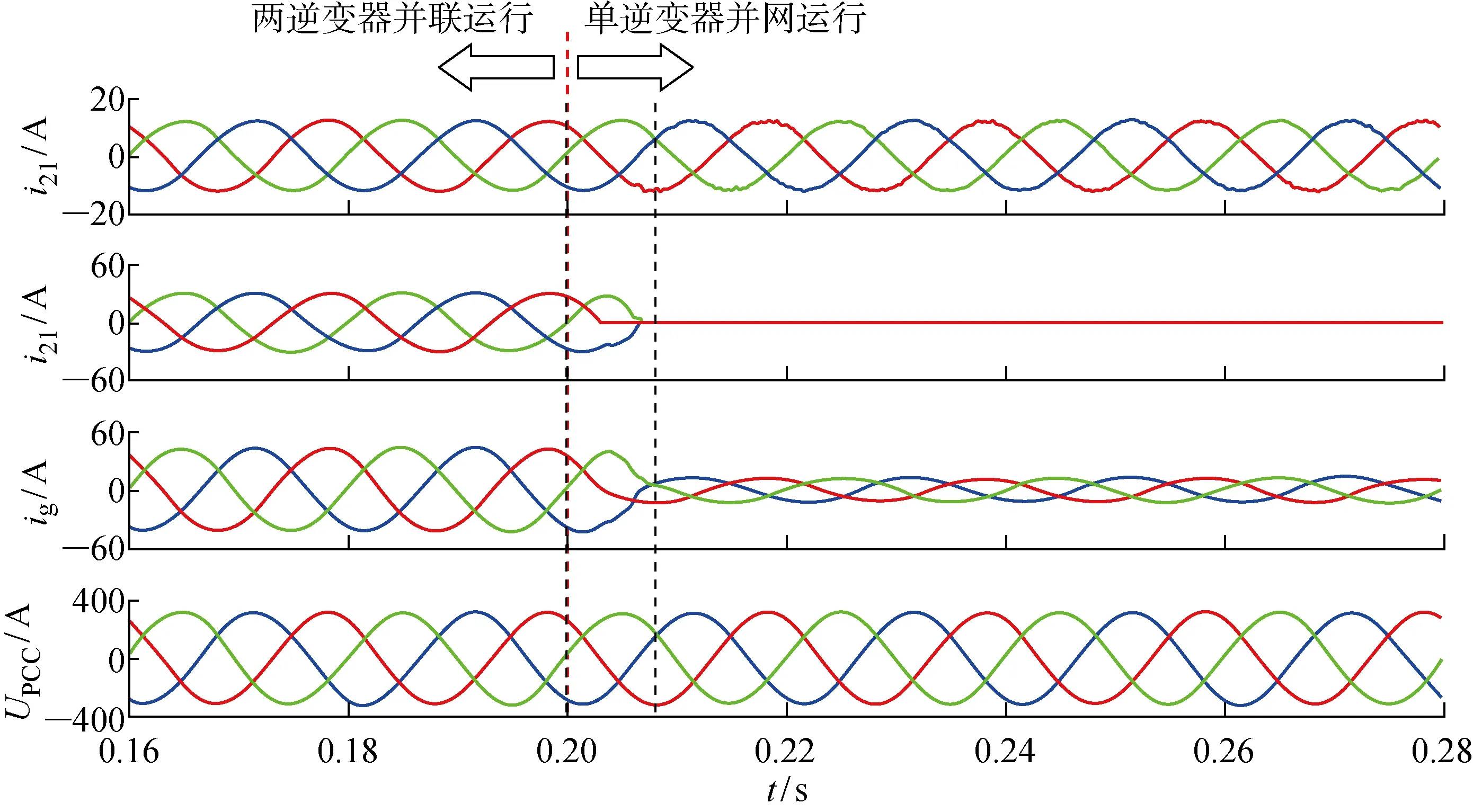
圖12 當逆變器2離網時仿真結果Fig.12 Simulation results when Inverter 2 is off grid

5 結論

針對弱電網條件下多逆變器并聯運行發生諧振的現象，對比研究了相同和不同容量逆變器并聯系統的諧振頻率特性.

(1) 多逆變器并聯系統的穩定性除受到與單臺逆變器并聯系統諧振點接近的公共諧振影響外，還受到交互諧振的影響.

(2) 相同額定容量逆變器并聯系統中，交互諧振僅受交互電流影響，公共諧振僅受公共電流影響，二者并未發生耦合；而不同額定容量逆變器并聯系統中，交互諧振和公共諧振分別受交互電流及公共電流的共同影響，二者存在耦合作用.

(3) 基于多逆變器并聯系統中的交互諧振，設計了數字陷波器，引入到傳統電容電流反饋有源阻尼控制中，實現了多諧振點的抑制，滿足了此類系統的并網要求.仿真結果驗證了所提策略的正確性和有效性.