人口普查漏報估計研究

胡桂華， 廖金盆， 范署姍， 葉寶紅， 吳 婷

(重慶工商大學數學與統計學院 經濟社會應用統計重慶市重點實驗室，重慶 400067)

1 引言

2020 年，中國、美國和其他許多國家將進行人口普查及其質量評估.普查漏報是評估目標之一.為指導各國政府統計部門開展普查漏報評估工作，聯合國統計司組織世界人口普查質量評估專家撰寫人口普查質量評估工作指南.該指南中的未匹配估計量只是包括了在質量評估調查中登記而未在普查中登記的漏報人口，從而低估總體普查漏報人口數.

為解決上述問題，本文在對現行普查漏報估計方法研究的基礎上，提出普查漏報合成估計量.該估計量由兩部分構成.第一部分是三個線性漏報估計量，估計未登記在普查人口名單但至少登記在質量評估調查人口名單及行政記錄人口名單之一的人數.第二部分是缺失單元漏報估計量，估計未登記在任何名單的人數.

創新體現在兩個方面.第一，相比目前國內外采用的估計普查漏報的逆記錄檢查估計量、未匹配估計量和平衡推算估計量，普查漏報合成估計量通過引入人口行政記錄，可以找到更多的普查漏報人口.首先，逆記錄檢查，需要在本次全國人口普查微觀數據庫搜索漏報人口，這是一項十分艱難的工作，而普查漏報合成估計量，只需要比對同一樣本普查小區的普查人口名單、質量評估調查人口名單及行政記錄人口名單，便可以獲得樣本漏報人口，工作難度小許多.其次，未匹配估計量，未包括同時遺漏于普查人口名單及質量評估調查人口名單的漏報人口，而普查漏報合成估計量同時包括遺漏于上述三份人口名單的人口.再次，平衡推算估計量，只能算出普查漏報人口數，而不能解釋形成漏報的原因及其漏報的程度，而普查漏報合成估計量，在比對三份人口名單后，可查明普查漏報的原因、程度及漏報在總體中的分布情況.探索普查漏報的發生機制，是漏報估計的主要目的.相比中國2010 年采用的未匹配估計量計算的樣本普查漏報率，普查漏報合成估計量，利用抽樣權數將樣本擴張到總體，估計總體的普查漏報率，并且采取刀切法近似計算抽樣方差.第二，在有限總體概率抽樣條件下，普查漏報的總體指標需要用樣本來估計.本文給出估計量的構造方法以及估計量的方差估計方法.

2 文獻綜述

普查覆蓋誤差包括普查凈誤差、普查多報與漏報[1].凈誤差定義為總體實際人數與普查登記人數之差.各國目前通行的做法是，用基于“捕獲-再捕獲”模型的雙系統估計量[2]構造總體實際人數估計量，把這個估計量與普查登記人口數之差當作人口普查凈誤差.未來可能用基于三次捕獲模型[3，4]的三系統估計量[5-7]來取代雙系統估計量[8-10].

凈誤差估計的研究成果多于普查漏報與多報.政府統計部門在其所發布的人口普查質量評估工作報告中只是簡單提及普查漏報的估計方法或估計結果.研究普查漏報估計的學術論文甚少.漏報有兩個特點.一是漏報人口未登記在普查表中，從普查表中得不到漏報人口信息，要構造漏報估計量，需要采取間接估計方法.二是各國人口普查質量評估結果顯示，普查漏報比多報嚴重.

逆記錄檢查估計量、未匹配估計量和平衡推算估計量，是估計總體普查漏報人口的傳統方法[11].采用逆記錄檢查估計量的國家包括加拿大、丹麥、芬蘭、危地馬拉、洪都拉斯、以色列、意大利、荷蘭、挪威、瑞典和美國.逆記錄檢查抽樣框由上次普查登記人口、上次普查漏報人口、上次到本次普查出生及遷入人口組成.樣本由人構成.對每一個樣本個人，在本次全國普查微觀數據庫搜索，尋找與其相同的人.如果找到，就稱該樣本個人為匹配人口，否則稱為未匹配人口，即普查漏報人口.逆記錄檢查估計量為樣本個人與其抽樣權數的線性估計量.其優勢是，由于逆記錄檢查與本次普查獨立，因而避免了因這兩項調查不獨立引起的交互作用偏差而低估或高估普查漏報人口數.其劣勢是自上次普查之后，樣本個人可能已經離開原來居住的地方，或者死亡、更改了姓名，找到他們有困難，難以判斷這些人是在本次普查中登記，還是漏報，或不屬于應該在本次普查中登記的人.這增加了逆記錄檢查實施的難度和錯誤判斷樣本個人在普查中登記情況的風險.

未匹配估計量為質量評估調查未匹配人口與其抽樣權數的線性估計量，或者質量評估調查人口數估計量與其匹配人口數估計量之差.匹配人口指，同時登記在質量評估調查名單與普查名單的人口.未匹配人口指，只登記在質量評估調查名單的人口.聯合國統計司建議各國使用未匹配估計量.中國在2010 年使用該漏報估計量估計現有人口、戶籍人口及常住人口的漏報率[12].未匹配估計量優勢在于，容易理解和實施.其劣勢是未包括同時遺漏于這兩份名單的人口，從而低估總體普查漏報人口數.如果樣本中的未匹配人口過少甚至為零，該漏報估計量提供的總體漏報人口數估計值可能嚴重偏離真值.

平衡推算估計量，依據公式“估計的凈誤差+估算的普查登記人口數=估計的普查漏報人數-估計的普查多報人數”間接推出總體普查漏報人口數[13].在人口普查中，有些住戶拒絕填寫普查表，或拒絕普查員上門登記.這類住戶的人口數一般通過鄰居，或其他熟悉情況的人估算.美國普查局把估算的普查登記人數，計入普查登記人口總數.美國在2010 年普查漏報估計中，在獲得凈誤差估計值(-3.6 萬人)、估算的普查登記人口數(599.2 萬人)，以及估計的普查多報人口數(1004.2 萬人)后，得到估計的普查漏報人口數為1599.8 萬人(Vincent Thomas Mule， 2012).平衡推算估計量的優勢是，可以很方便地推出普查漏報人口數.其缺陷有4 個：

① 不能提供本次普查登記過程中的漏報人口信息，不利于下次普查及其質量評估工作方案的改進；

② 凈誤差與普查多報估計對普查正確登記位置認定標準不一致，即前者要求每個人登記在其所屬的樣本小區，或其周圍區域內，而后者可以登記在研究區域的任何地方.這種不一致影響普查漏報估計精度；

③ 內含交互作用偏差的雙系統估計量估計的凈誤差存在一定程度的偏誤，這種偏誤造成疊加效應，影響普查漏報估計精度；

④ 估算的普查登記人口數存在一定程度的估算誤差，降低普查漏報估計精度.

從對普查漏報合成估計量創新情況的論述，以及對現有普查漏報估計量利弊的分析，不難看出，普查漏報合成估計量是一種相對較為理想的普查漏報估計方法，有望應用于人口普查漏報估計.中國計劃在2020 年首次使用普查漏報合成估計量.

3 普查漏報合成估計量理論

為構造普查漏報合成估計量，在獲得普查人口名單、質量評估調查人口名單及行政記錄人口名單后，要做好五項工作.第一，每份名單只能登記普查目標總體的人.如果有的名單重復登記或登記普查標準時點不存在的人，就予以剔除.行政記錄人口名單要利用多個來源的人口名單建立，并剔除其中的重復人口.對名單中存在但懷疑可能已經死亡的人，在現場核實的基礎上決定剔除還是保留.第二，分析普查漏報的可能情形，即只登記在質量評估調查或行政記錄的人口(共3 種)，未登記在任何名單的人口(1 種).其中，前3 種漏報人口數使用線性漏報估計量估計，后1 種漏報人口數采用缺失單元漏報估計量估計.普查漏報合成估計量為三個線性漏報估計量與一個缺失單元漏報估計量[14-16]的總和.第三，比對三份人口名單，為構造三個線性漏報估計量及一個缺失單元漏報估計量提供數據.假定不存在比對誤差，否則要測算比對誤差對普查漏報合成估計量的影響.第四，采用加權優比排序法[17]，選擇對總體人口等概率分層的變量，例如，性別、年齡、房屋所有權、居住地點、民族，把登記概率大致相等的人口放在同一層.顯然，變量越多，交叉層的層數也越多，分配到每一個交叉層的樣本人口就越少，普查漏報估計值的抽樣誤差就越大[18].為控制交叉層數目，分層變量的數目應該減少.分層變量的選擇是一項復雜的工作，超出本文研究范圍.對此問題有興趣的讀者，請見參考文獻[17].把每一個交叉層稱之為等概率人口層.在每個等概率人口層，建立普查漏報合成估計量及其抽樣方差估計量.匯總所有等概率人口層的普查漏報合成估計量，得到總體的普查漏報合成估計量.匯總所有等概率人口層的普查漏報合成估計量的抽樣方差及等概率人口層之間的協方差，得到總體的普查漏報合成估計量的抽樣方差.等概率人口層之間的協方差可能為正或為負.第五，構造三份名單全面登記、抽樣登記、人口移動和無人口移動的缺失單元漏報估計量、線性漏報估計量及普查漏報合成估計量.

用v 表示任意等概率人口層，V 為總層數.為了敘述方便，在下面的式(1)-(26)省去v.在構造總體普查漏報估計量時，在式(27)-(30)添加v 和V.

用xcqa表示等概率人口層的人口登記在三份名單的人口數，下標c， q， a 分別表示普查、質量評估調查和人口行政記錄，取值1 或0.c=1 表示等概率人口層的人口在普查人口名單，c=0 表示等概率人口層的人口不在普查人口名單.q =1 表示等概率人口層的人口在質量評估調查人口名單，q =0 表示層v 的人口不在質量評估調查人口名單.a=1 表示等概率人口層的人口在行政記錄人口名單，a = 0 表示層v 的人口不在行政記錄人口名單.用這些記號寫出如下有關的估計量.

3.1 等概率人口層的缺失單元漏報估計量

我們分三個層次討論問題.第一層次，假定普查人口名單、質量評估調查人口名單及行政記錄人口名單是對總體人口的全面登記，并且三份名單所登記的是各小區普查時點的同一常住人口總體.第二層次，仍假定三份名單對總體全面登記，并考慮普查日與質量評估調查日之間的人口移動.第三層次，用有限總體概率樣本資料，構造上面兩個層次的缺失單元漏報估計量的構成元素的估計量[19].

3.1.1 全面登記且無人口移動的缺失單元漏報估計量

缺失單元漏報估計量，依據普查人口名單、質量評估調查人口名單及行政記錄人口名單的統計關系建立.三份名單可能的統計關系分為四類.第一類是三份名單條件獨立.例如，普查與質量評估調查相關，質量評估調查與人口行政記錄相關，普查與行政記錄獨立.這類關系共有3 種.第二類是三份名單聯合獨立.例如，普查與質量評估調查相關，這兩項調查與行政記錄獨立.這類關系也有3 種.第三類是三份名單兩兩相關，這類關系有1 種.第四類為三份名單相互獨立，這類關系有1 種.

構造缺失單元漏報估計量有兩個方法.第一個方法是，用三系統估計量構造三份名單的缺失單元漏報估計量.由于三系統估計量在三個名單統計關系不同的情況下有不同的計算公式，所以需要先使用對數線性模型，判斷三份名單屬于何種統計關系，然后使用該種統計關系下的三系統估計量計算公式.第二個方法是，根據先驗信息分析三份名單最可能形成的統計關系，并只構造這種統計關系的缺失單元估計量.普查與質量評估調查相關，但它們與人口行政記錄獨立，這種統計關系的可能性大.事實上，這兩項調查由政府統計部門組織實施，而人口行政記錄來源于不同于政府統計部門的行政部門.另外，這兩項調查的目的是為了獲得人口數，而人口行政記錄是行政工作的副產品，用于行政管理.例如，我國戶籍資料本身并不是為了提供人口數，而是為了實現對人的管理，控制人口向大城市流動，合理布局全國人口分布.基于此種分析，只構造該種統計關系的缺失單元漏報估計量.為構造缺失單元普查漏報估計量，需要把普查和質量評估調查合并在一起當作第一個來源，把人口行政記錄當作第二個來源.由于數據來源的特點，它們合并后獨立于人口行政記錄.不在第一個來源但在第二個來源的人口數用x001表示，在第一個來源不在第二個來源的人口數用(x110+x100+x010)表示，同時在兩個來源的人口數用(x111+x101+x011)表示，未登記在任何來源的人口數用x000表示，其估計量稱為缺失單元漏報估計量，用^x000表示.把這四項填寫在表1.

表1 兩來源的等概率人口層數量

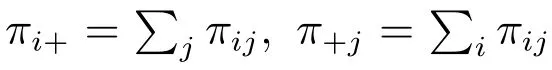
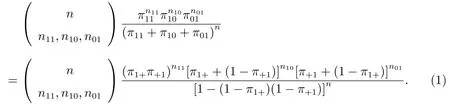
式(1)中的n=x111+x101+x011+x110+x100+x010+x001.總體中的人至少在兩個來源之一的概率為[1-(1-π1+)(1-π+1)].單元(i，j)人數的另外一種表達式為概率函數的二項分布為

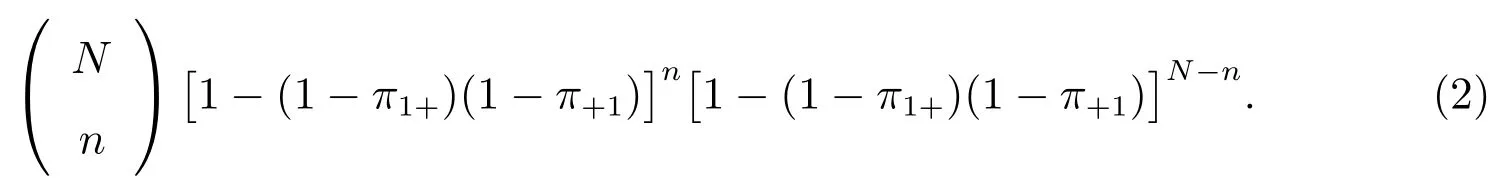
如果給出π1+， π+1， Nv，那么π1+， π+1的最大似然估計量分別為

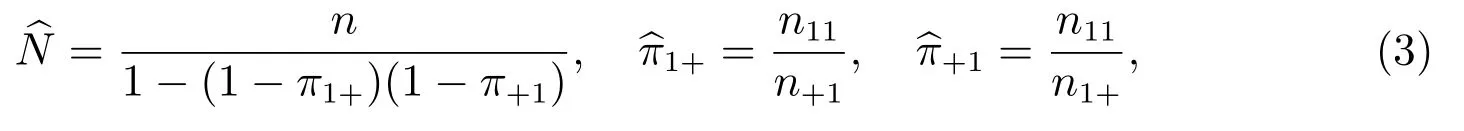
式(3)中，n+1=n11+n01， n1+=n11+n10.

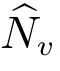
由于N =n+x000，所以

將式(4)及n 代入式(5)得到

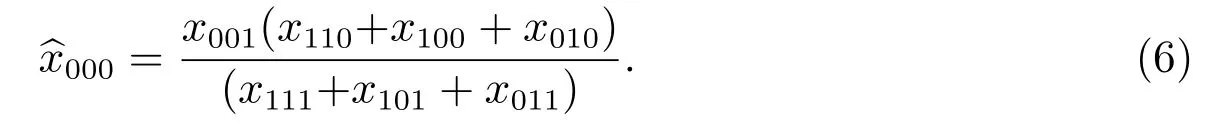
式(6)是三份名單對總體全面登記的缺失單元估計量.

3.1.2 全面登記且人口移動的缺失單元漏報估計量

在人口普查質量評估中，質量評估調查通常滯后于人口普查半個月左右.在這期間，會有人從其他普查小區移動到本小區，也有人從本小區移動到其他小區，還有人一直居住在本小區.把這三種情況的人分別稱為向內移動人口、向外移動人口和無移動人口.質量評估調查人口名單的人口有兩種構成方式.一是無移動人口和向外移動人口，簡稱質量評估調查-A.另外一種方式是無移動人口和向內移動人口，簡稱質量評估調查-B.質量評估調查-A 的優勢是實現了人口普查質量評估追溯普查標準時點的人口及其人數的目的，缺點是找到向外移動人口有難度，其有關信息只能通過鄰居或估算方法獲得，誤差較大.質量評估調查-B 的優勢是向內移動人口在本小區，獲取其質量評估調查時信息較容易，劣勢是獲得其普查標準時點在其他普查小區的信息有一定困難.如果采用質量評估調查-A，那么式(6)中的每項人口數要更改為無移動人口數與向外移動人口數的和.如果采用質量評估調查-B，那么式(6)中的每個人口數要更改為無移動人口數與向內移動人口數的和.用n， i， o 分別表示無移動人口、向內移動人口和向外移動人口.

如果采取質量評估調查-A，那么式(6)變為

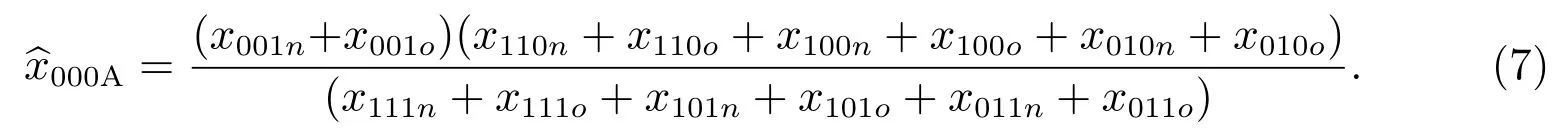
對本小區，向外移動人口在質量評估調查標準時點前已經離開了本小區，不可能登記在本小區的質量評估調查人口名單中，因此式(7)變為

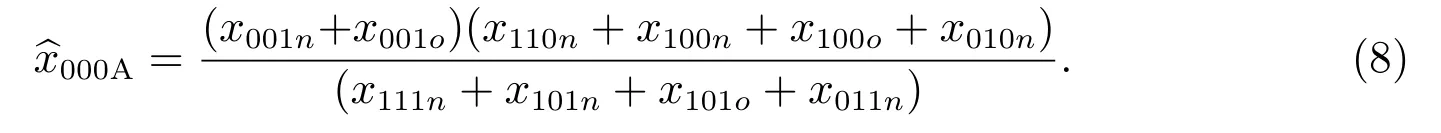
如果采用質量評估調查-B，那么式(6)變為

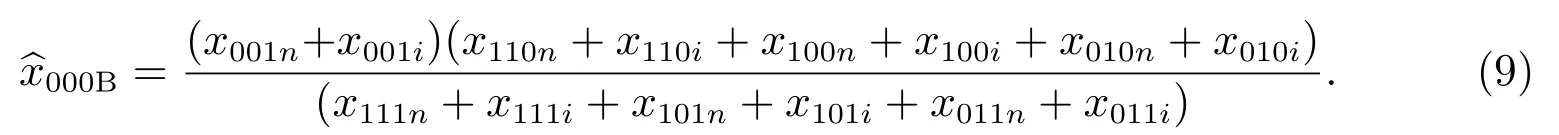
同樣，對本小區，向內移動人口無法登記在本小區的行政記錄人口名單，因此式(9)變為

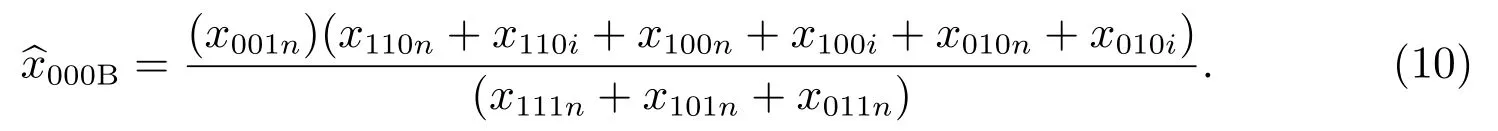
3.1.3 抽樣登記且人口移動的缺失單元漏報估計量

在質量評估調查為全面調查情況下，以上各式等號右邊的每一數據項都是層v 的總人口數指標.為了節約成本、時間，減少非抽樣誤差，各國政府統計部門的質量評估調查實際上是從全國或各省或各行政區的普查小區總體中抽取樣本普查小區來進行的.在質量評估調查為抽樣調查及考慮人口移動情況下，式(8)和式(10)的每一數據項要用估計量來表示，用有限總體概率樣本來構造，即先將每一樣本小區的人口數與其抽樣權數相乘，然后相加.如果對樣本小區人口100%抽樣，而且不存在無答復，那么樣本普查小區的抽樣權數等于其中每人的抽樣權數.此時式(8)變為

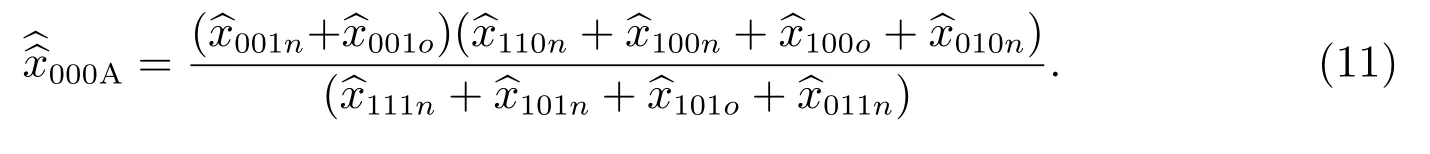
式(10)變為

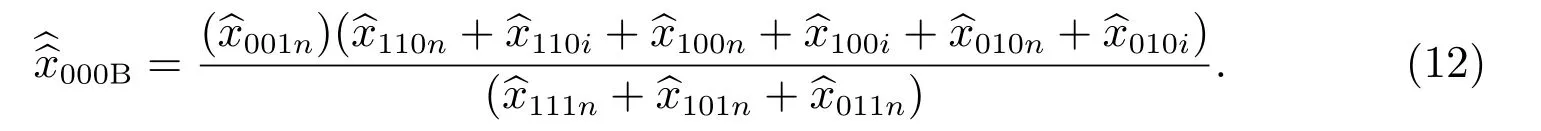
3.2 等概率人口層的線性漏報估計量

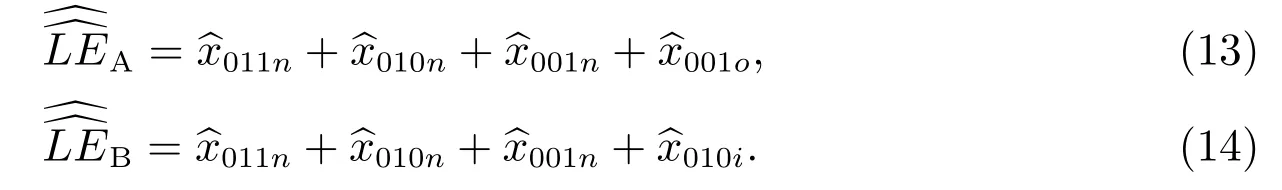
3.3 等概率人口層的普查漏報合成估計量

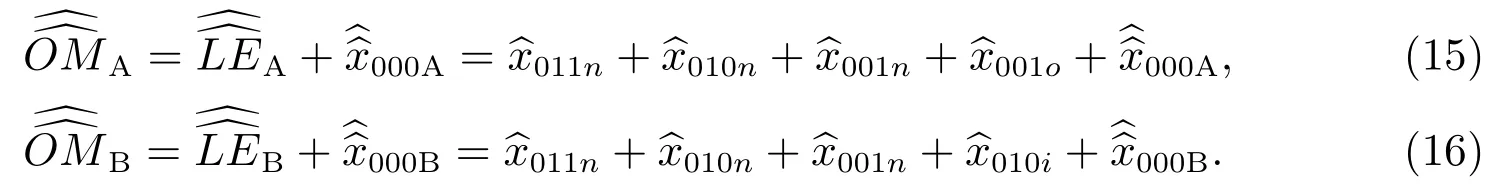
式(11)-(16)等號右邊的每一個估計量，依據質量評估調查樣本數據來計算.在人口普查質量評估抽樣調查中，樣本的抽取方法有分層整群抽樣、分層多階段抽樣和分層多重抽樣[20-22].中國自1982 年人口普查質量評估起，一直采用分層整群抽樣方法抽取普查小區樣本.本著研究服務于應用的原則，本文采取分層整群抽樣.在該抽樣法下，式(11)-(16)的每一個估計量統一用式(17)來表示.

式(17)中，H 表示對總體全部普查小區所分的層數，例如按照普查小區規模將總體中的所有普查小區分在三層，每一層h 的樣本規模記為nh， h = 1，2，··· ，H，yhi為小區hi 在等概率人口層的人數.在分層整群等概率抽樣下，樣本普查小區hi 的抽樣權數whi為

3.4 等概率人口層的普查漏報合成估計量的抽樣方差估計量

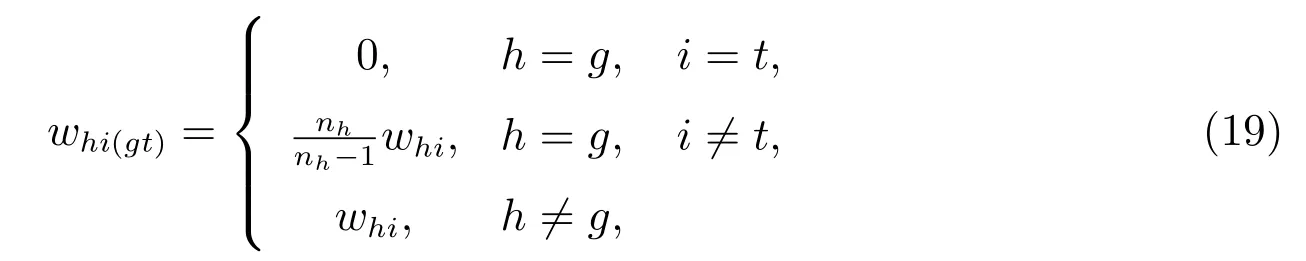
式(11)和(12)，以及式(15)和(16)的復制估計量分別為

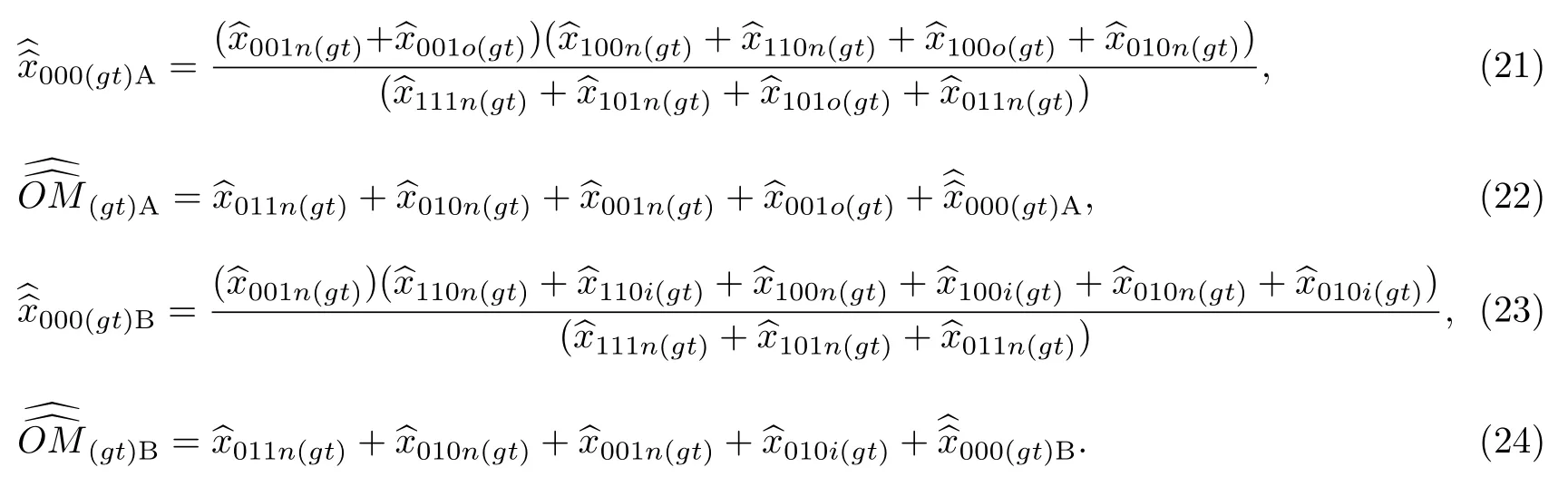
式(15)和(16)的分層刀切抽樣方差(variance， 縮寫為var)估計量分別為

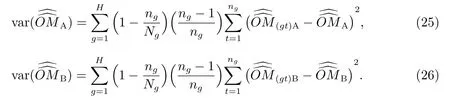
為了正確理解及使用式(25)和式(26)，需要注意兩點.第一，刀切法僅在樣本內操作.切掉一個單位，只不過是這個切掉的單位不在樣本中，并不意味著它不在總體中.如果把這個單位從總體中切掉，調查對象就改變了，就不再是原來的總體了，與現在的調查任務就不一樣，所以從樣本中切掉一個單位，只不過是假定了一個虛擬樣本，即切掉的那個單位沒有進入這個虛擬樣本.就未分層整群抽樣來說，假定從單位數為N 的總體中簡單隨機抽取單位數n.現在從該樣本中切掉1 個單位，在計算其它(n-1)個單位各自的復制權數時，應該是從N 個單位中簡單隨機抽取(n-1)個單位概率的倒數，此時總體單位數目不改變，只是樣本單位數目減去1.即這(n-1)個單位此時各自的復制權數是N/(n-1).第二，同計算復雜總體參數估計量抽樣方差的泰勒線性方差估計量相比[25，26]，刀切法操作便利，容易實施，在計算了樣本普查小區的復制權數及總體參數估計量的復制估計量后，將樣本數據代入其中即可算出結果.

3.5 總體普查漏報合成估計量及其抽樣方差估計量

在構造了每個等概率人口層(用v 表示)的普查漏報估計量后，下一步要做的工作是匯總所有等概率人口層(用V 表示總層數)的普查漏報合成估計量及其抽樣方差估計量，得到總體的普查漏報合成估計量及抽樣方差估計量.

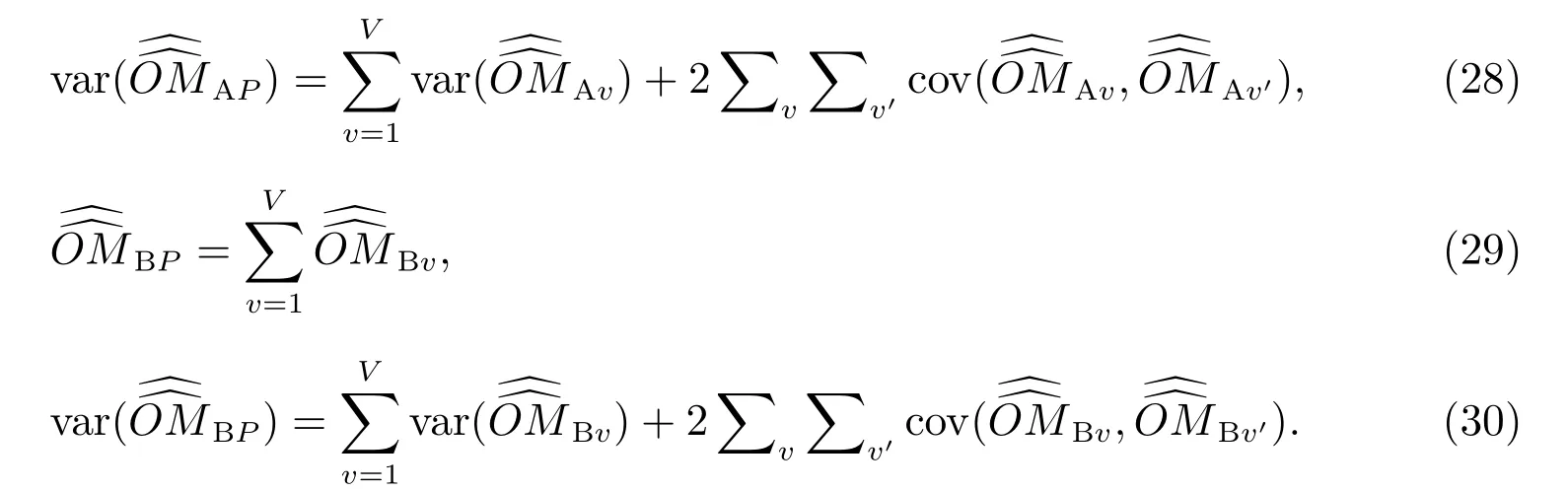
4 未匹配估計量

為了比對普查漏報合成估計量與傳統普查漏報估計量在數據估計精度上的優勢，以及考慮進行這種比對所需數據資料的可得性，我們現在討論未匹配估計量.除美國等少數幾個國家外，其他國家都是使用這種估計量.與普查漏報合成估計量相比，未匹配估計量不用對總體人口等概率分層，直接在總體人口內構造及使用.

未匹配估計量建立的關鍵是獲得匹配人口.對樣本普查小區的普查人口名單及質量評估調查人口名單，如果后者名單中的某人出現在普查人口名單，就稱其為質量評估調查人口名單的匹配人口，如果后者名單中的某人未在普查人口名單中出現，就稱為后者的未匹配人口[27].未匹配人口為普查漏報人口.做出上述判斷的一個假定條件是，質量評估調查人口名單中的每一個人屬于普查目標總體，應該在普查中登記.在人口普查質量評估中，各國政府統計部門默認質量評估調查人口名單完美無缺.

為區別普查漏報合成估計量的總體P，這里用U 表示總體的未匹配估計量.

4.1 總體未匹配估計量

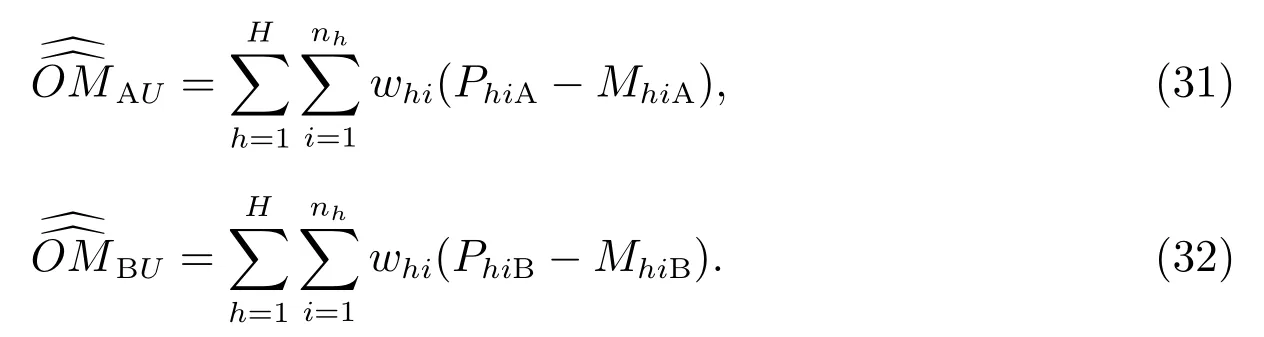
式(31)和(32)，PhiA和MhiA分別表示質量評估調查-A 的無移動人口和向外移動人口的數目之和，以及它們的匹配無移動人口和向外移動人口的數目之和；PhiB和MhiB有同樣的相應解釋.whi依據式(18)計算.

4.2 總體未匹配估計量的抽樣方差估計量

雖然式(31)和式(32)有方差數學表達式計算其抽樣方差，但為了與普查漏報合成估計量的抽樣方差進行數據上的可比性比較，我們使用分層刀切法近似計算其抽樣方差.文獻[19]指出，線性估計量的抽樣方差可以用分層刀切法計算.

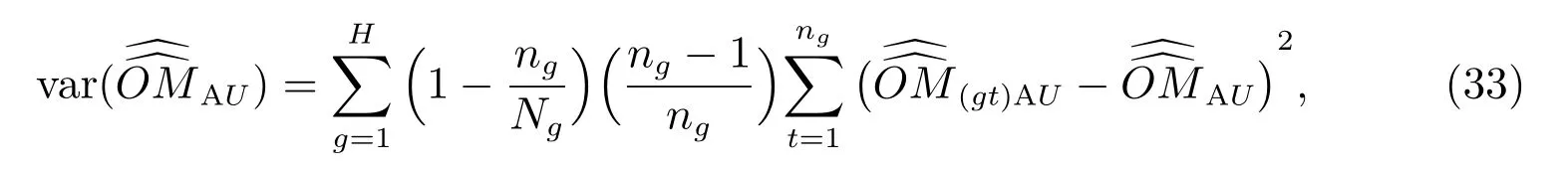
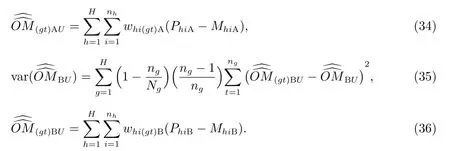
式(34)和(36)中的whi(gt)根據式(19)計算.不難看出，未匹配估計量的抽樣方差計算，無需在等概率人口層內進行，可以直接在總體內計算.

5 實證分析

實證對象為廣西南寧市邕寧區，資料所屬時間是2010 年11 月1 日零時，目標是估計邕寧區普查漏報.在樣本抽取前，將邕寧區所有普查小區劃分在三層：蒲津社區層；那樓社區和新江社區合并層；百濟社區和中和社區合并層.在每層，以普查小區為抽樣單位，從邕寧區的1038 個普查小區中簡單隨機抽取7 個，并獲得了樣本小區的普查人口名單、質量評估調查人口名單和行政記錄人口名單.通過比對，獲得同時登記在三份名單、兩份名單及一份名單的人口數.對每個樣本小區的人口，按照性別分在兩個等概率人口層，即男性層和女性層.在這兩個層計算普查漏報估計值.

5.1 基于普查漏報合成估計量的估計結果及數據分析

5.1.1 樣本資料

樣本普查小區及樣本人口數資料見表2 至表5.

5.1.2 加權人數計算

利用表2 至表5 樣本數據，使用式(17)計算式(11)和(12)，以及式(15)和(16)每項的加權人數，見表6.

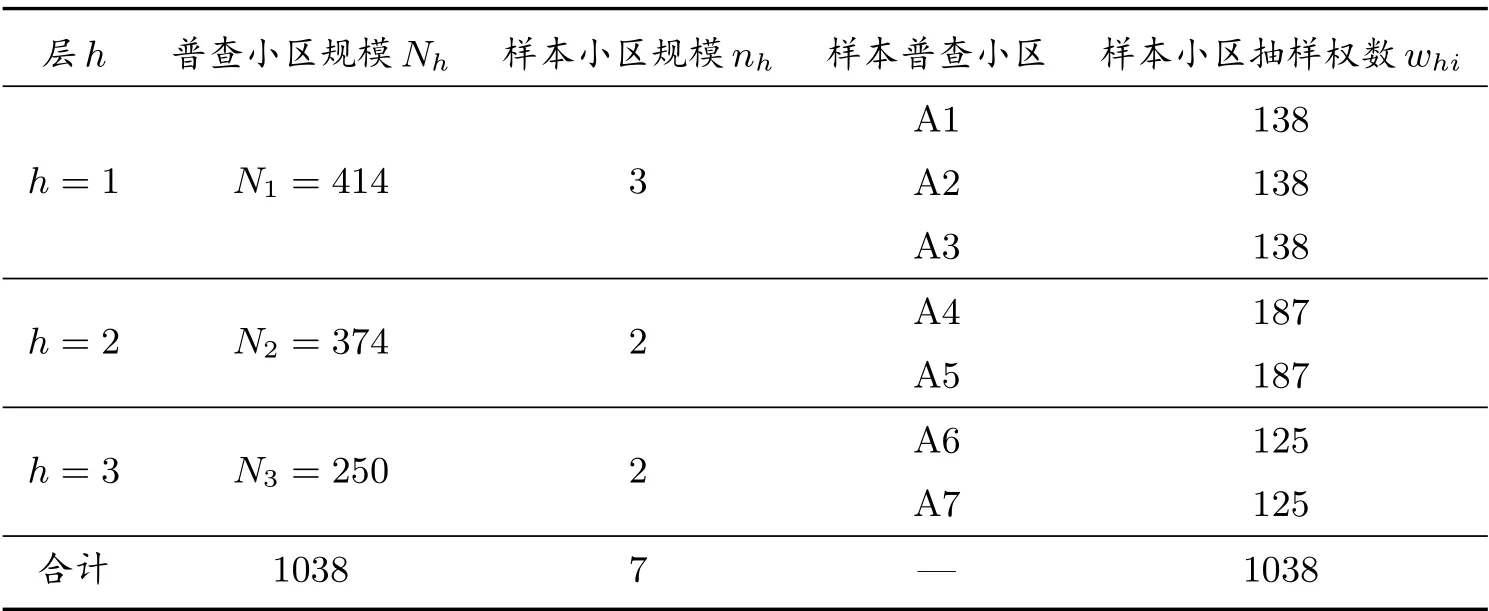
表2 分層及樣本

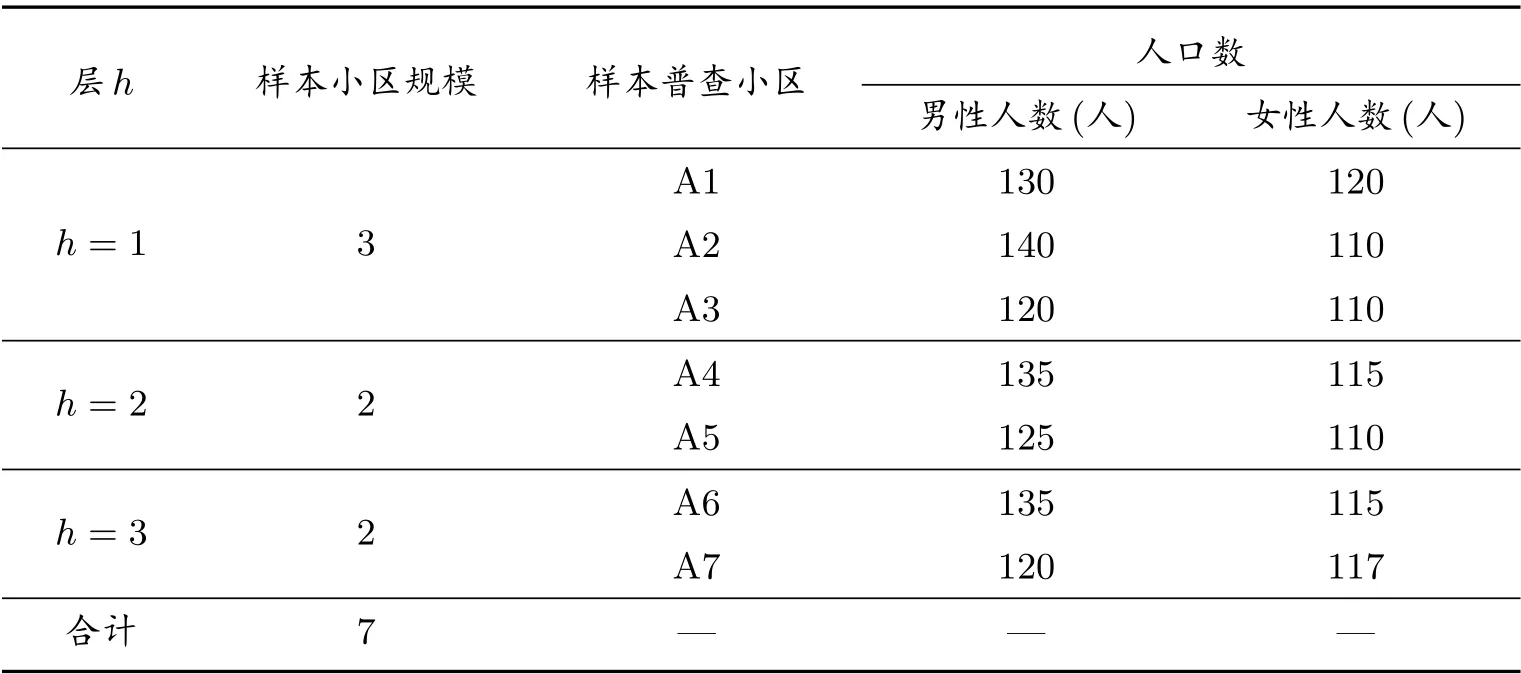
表3 樣本普查小區人口數

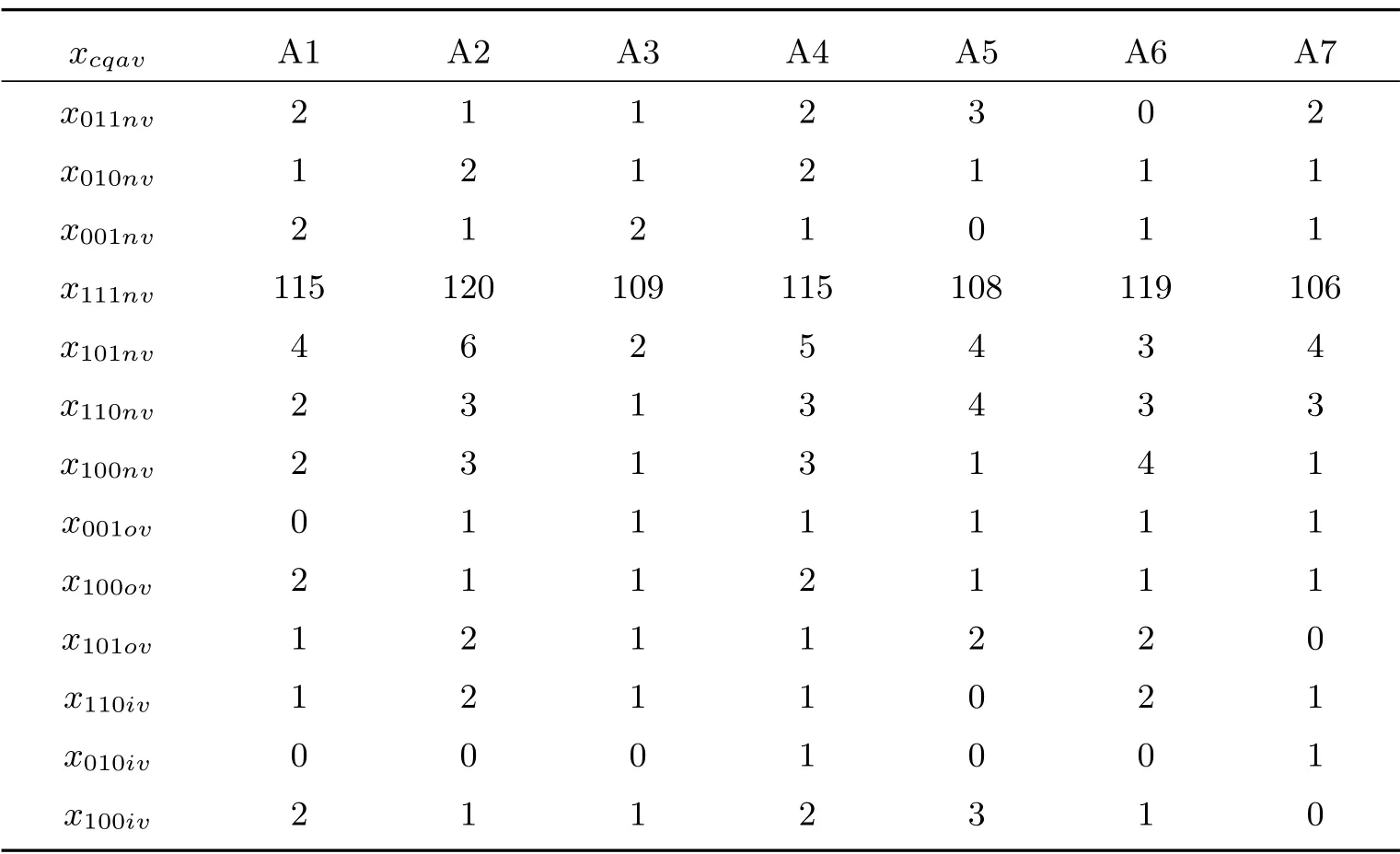
表4 樣本普查小區男性在三份名單登記的人數(人)

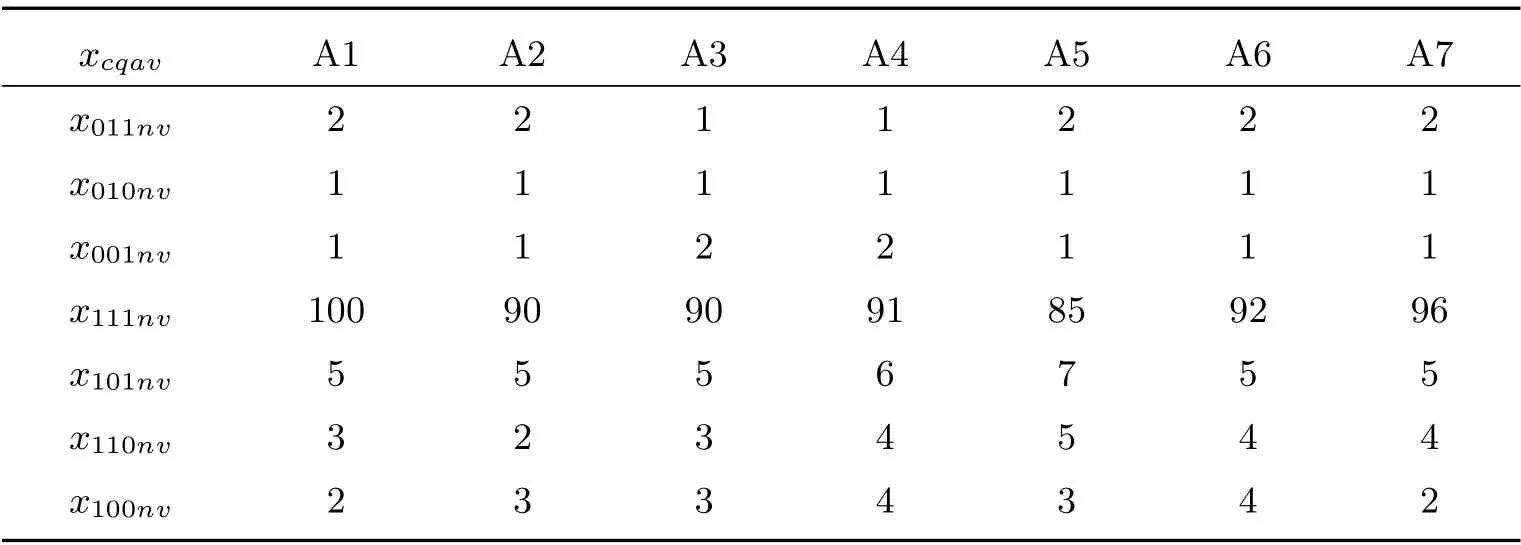
表5 樣本普查小區女性在三份名單登記的人數(人)

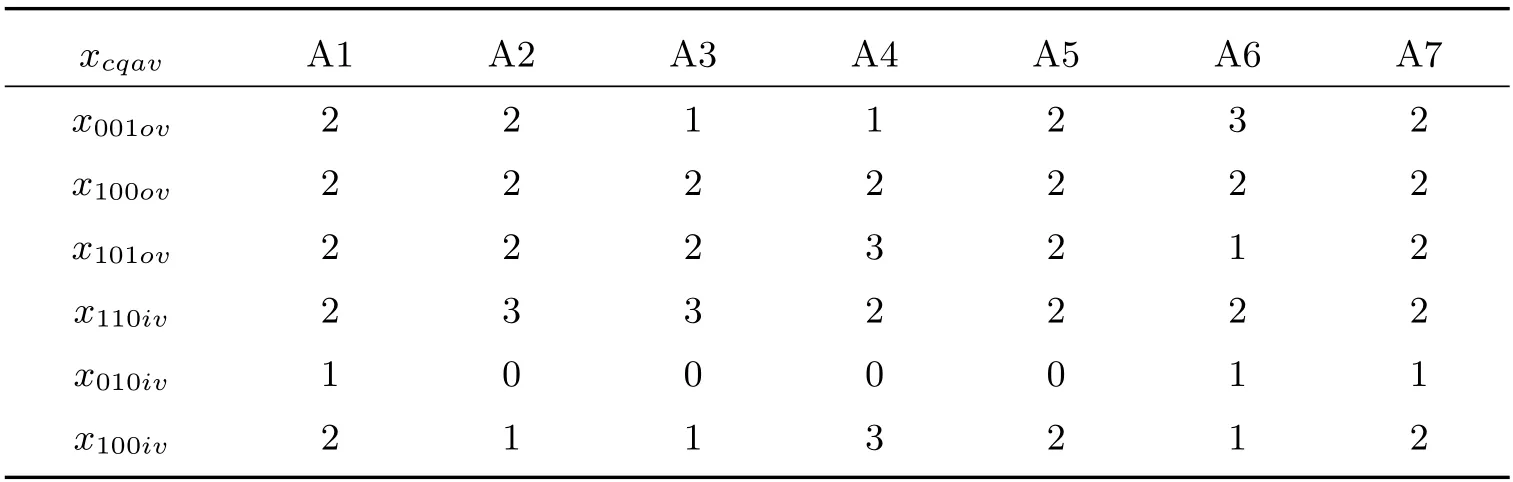
續表5 樣本普查小區女性在三份名單登記的人數(人)

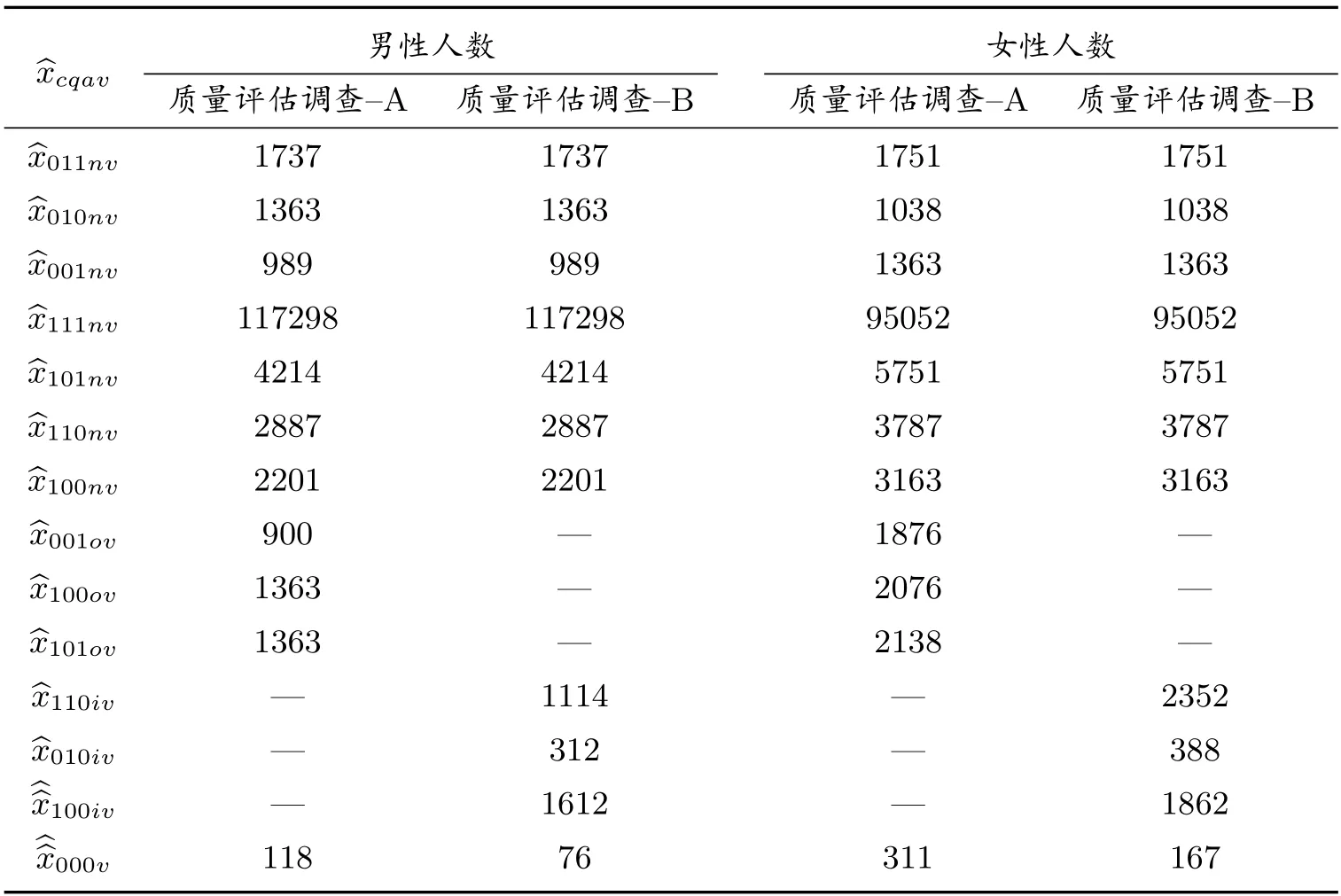
表6 等概率人口層在三份人口名單每項的加權人數(人)

5.1.3 普查漏報計算

使用式(22)-(24)，利用表6 數據，計算男性層和女性層的普查漏報人數.利用式(27)-(29)計算總體普查漏報人口數.計算結果見表7.

表7 表明，如果采取質量評估調查-A，男性層和女性層的普查漏報人口數分別為5107 人和6339 人.如果采取質量評估調查-B，男性層和女性層的普查漏報人口數分別為4477 人和4707 人.如果采取質量評估調查-A 或-B，總體普查漏報人口數分別為11446 人或9184 人.因此，無論男性層、女性層，還是總體，質量評估調查-A 的普查漏報人口數均大于質量評估調查-B.這一現象表明，所選取的樣本普查小區的向外移動人口多于向內移動人口.由于樣本小區是隨機選取的，所以邕寧區的向外移動人口比向內移動人口多.“六普”數據分析顯示，廣西南寧市邕寧區的一些中青年去廣東、北京、上海、浙江、深圳打工，而來邕寧區打工的很少.在普查與質量評估調查之間，邕寧區人口也是以向外移動為主.可見，本文計算結果與“六普”結果一致.

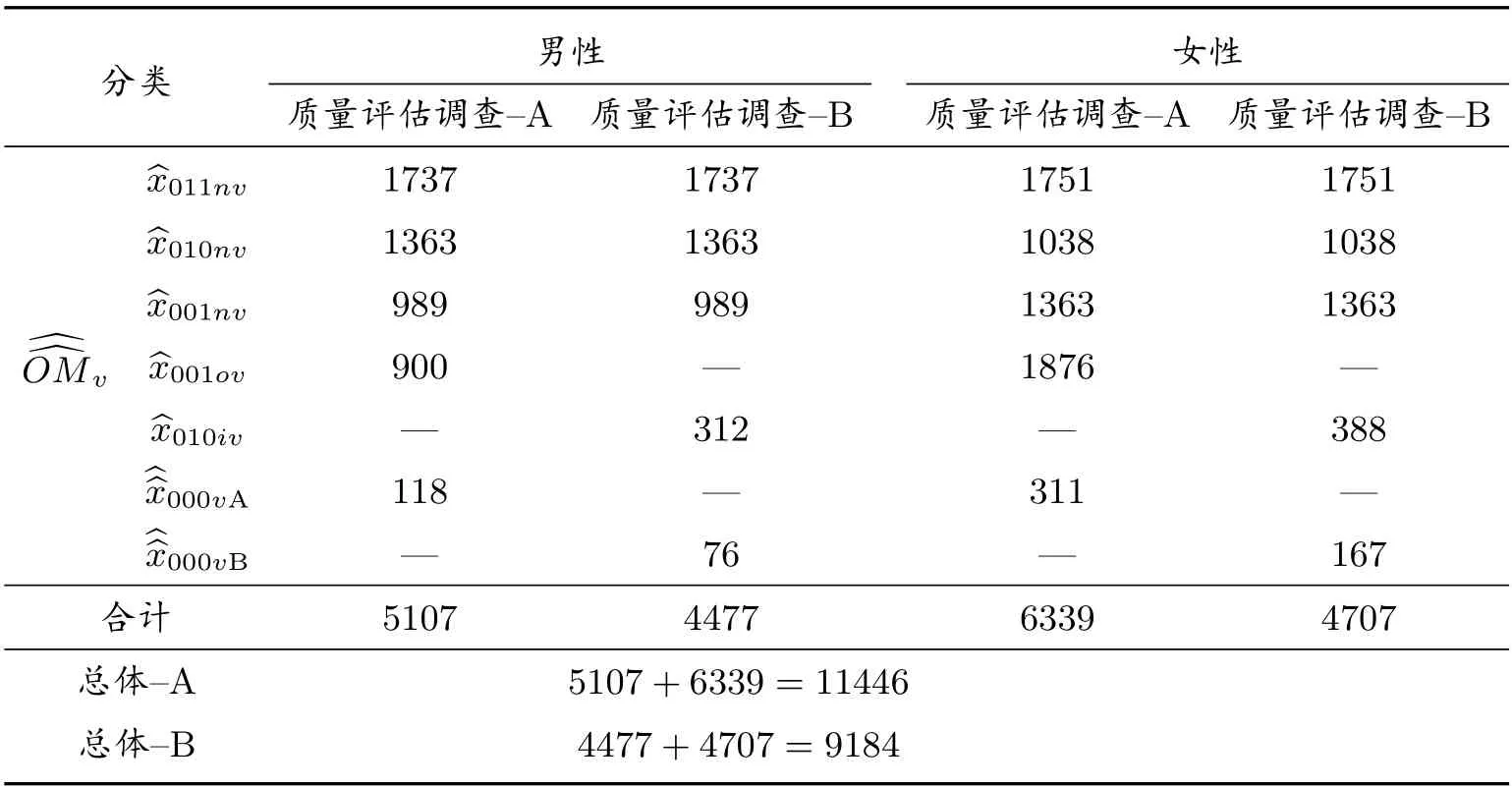
表7 普查漏報人數(人)

5.1.4 普查漏報估計值的抽樣方差計算

在計算了男性和女性及總體的普查漏報估計值之后，還要使用分層刀切法計算其抽樣方差估計值.這包括三個步驟.第一步，使用式(19)計算每刀切掉每一層的每一個樣本普查小區后，所有樣本普查小區的復制權數，計算結果見表8.在分層整群抽樣下，刀切對象是每一層的所有樣本普查小區.如果采取整群二重抽樣，刀切的對象是第一重樣本的所有普查小區，而不是第二重樣本的所有普查小區.第二步，依據式(20)計算式(21)-(24)每一個數據項的復制估計量，例如刀切第一層的第一個樣本普查小區A1 后的每一個數據項的復制估計量，計算結果見表9.為節省篇幅，省去依次刀切A2-A7 樣本普查小區后得到的每個數據項.利用表9 數據，使用式(21)-(24)計算“缺失單元人數復制值及漏報復制值”，計算結果見表10.為了計算普查漏報抽樣方差，寫出依次刀切A1-A7 的普查漏報復制估計值及普查漏報估計值，見表11.第三步，利用表11 數據，使用式(25)、式(26)、式(28)、式(30)計算男性層、女性層，以及總體的抽樣方差與協方差.結果請見表12.

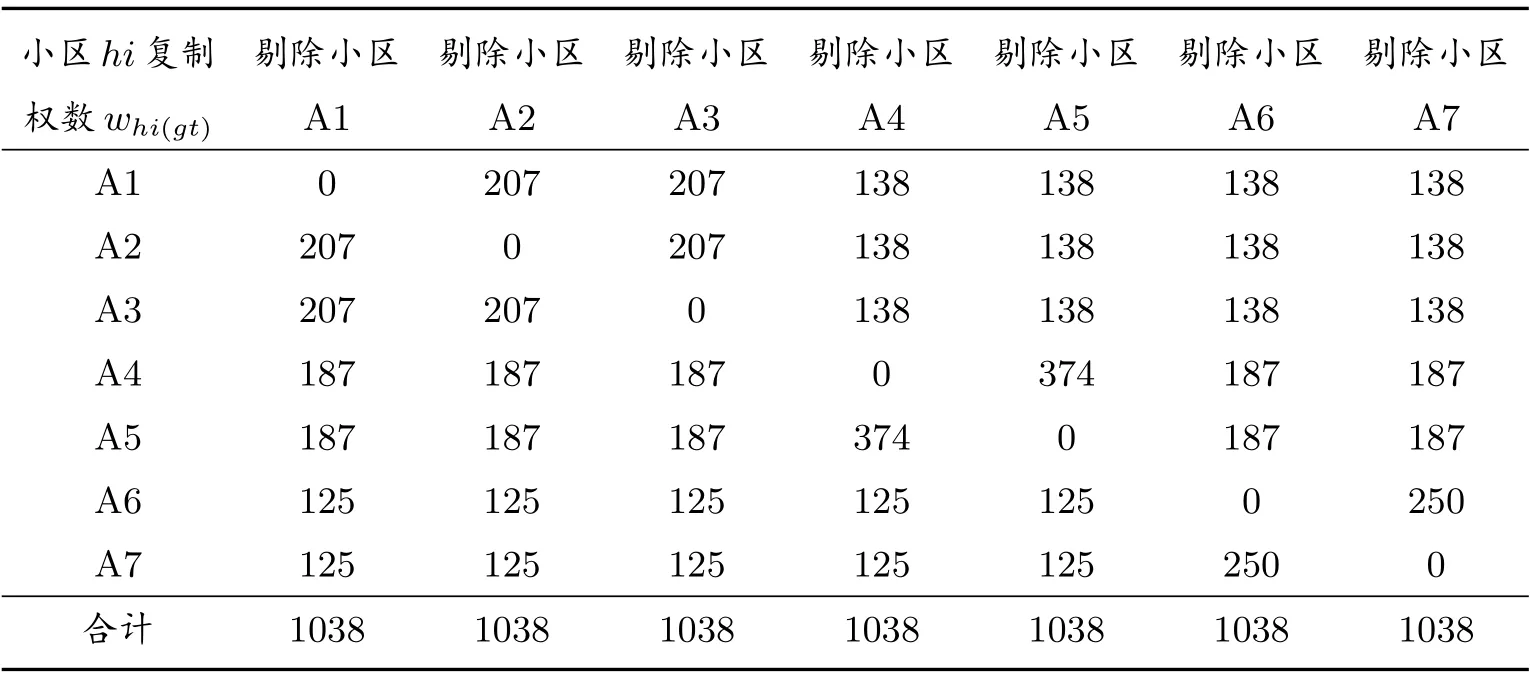
表8 樣本普查小區的復制權數

從表8 可以看出，無論剔除哪一個樣本普查小區，所有樣本普查小區的復制權數之和與未剔除任何小區的所有樣本小區的抽樣權數之和相等.這說明，剔除某個樣本小區后，總權數不變，但有些樣本小區的權數變大，也有的樣本小區權數變小，還有的小區權數不變.利用這些規律可以驗證復制權數的計算是否正確.復制權數功能有三個.一是計算式(11)和(12)，以及式(15)和(16)每一個估計量的復制值.二是計算普查漏報復制估計值.三是計算普查漏報估計值的抽樣方差.

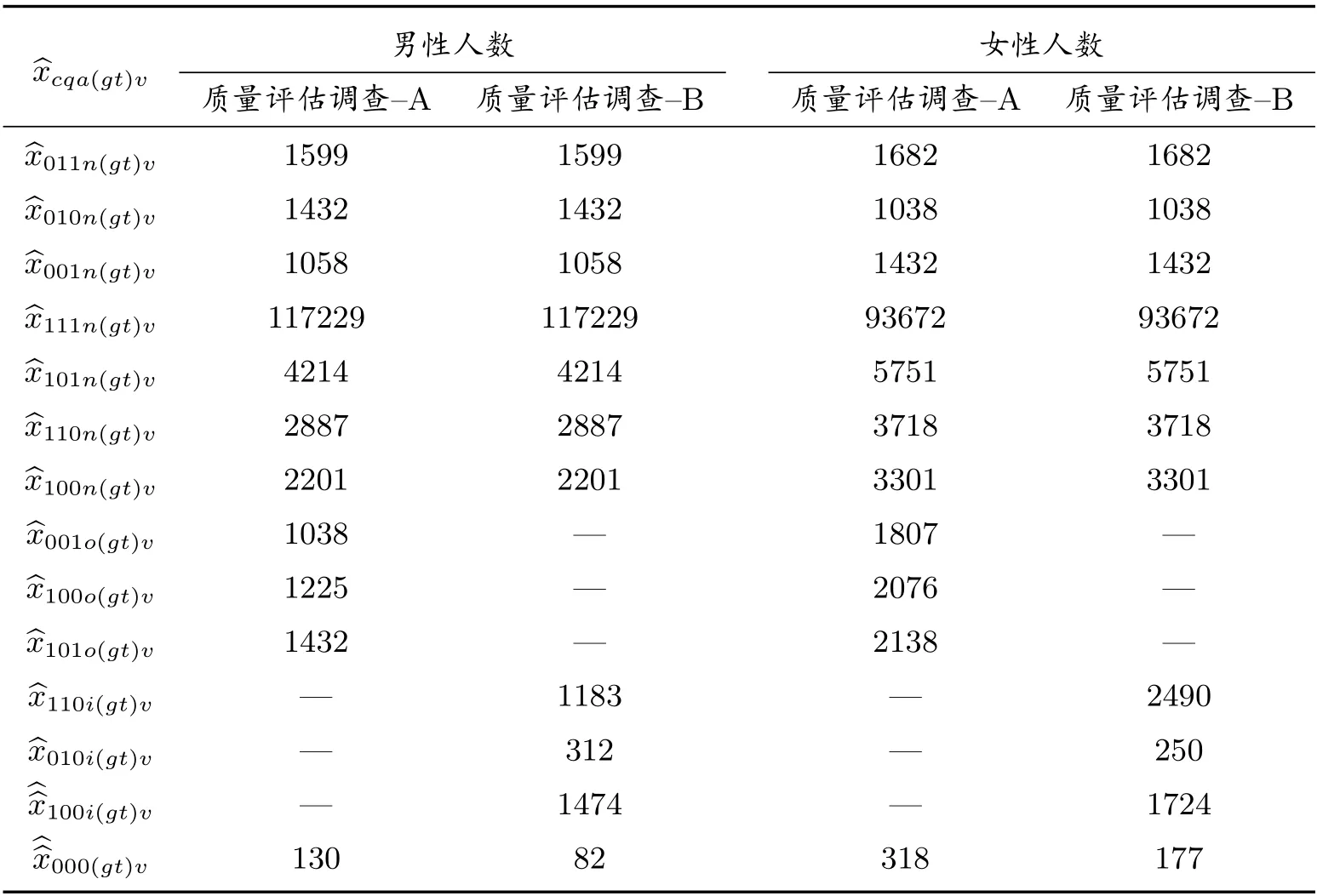
表9 等概率人口層在三份名單的復制加權人數(人)(剔除t=A1)

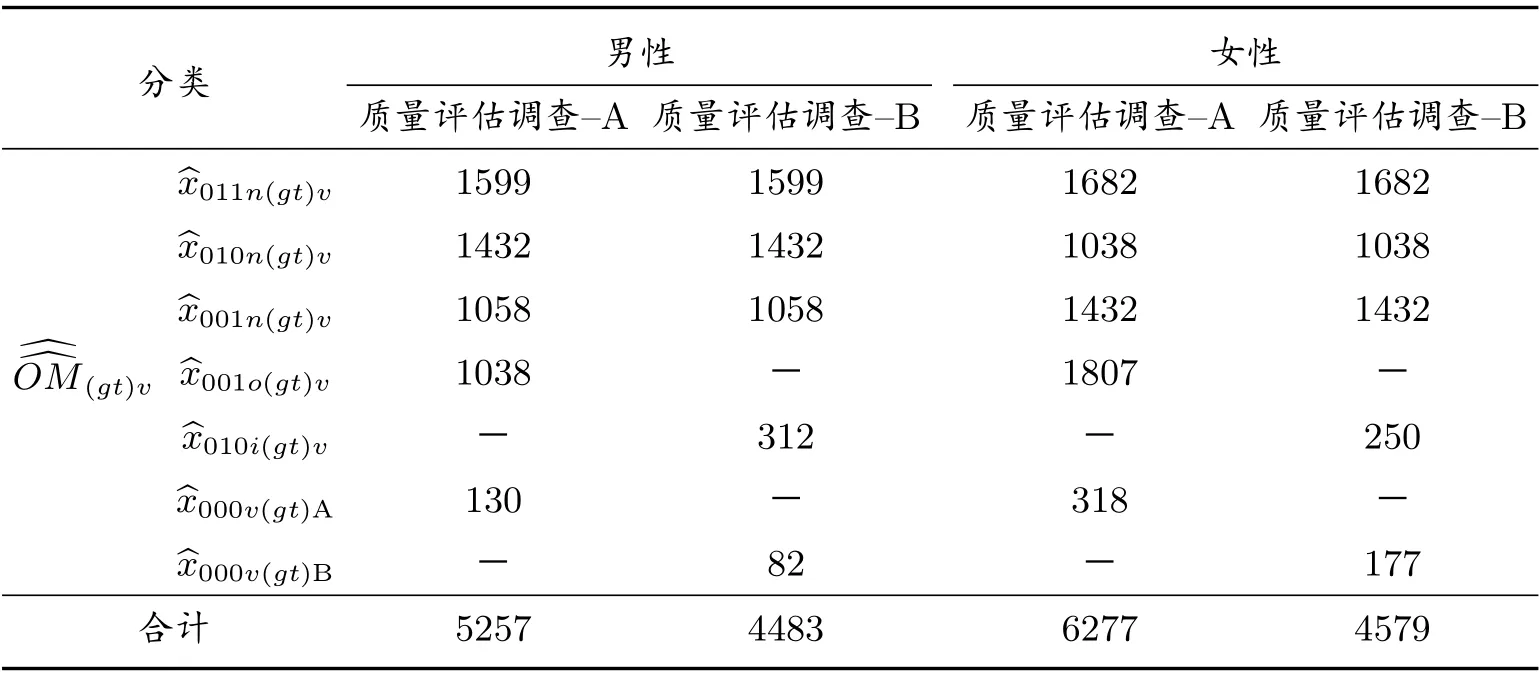
表10 普查漏報復制人數(人)(剔除t=A1)

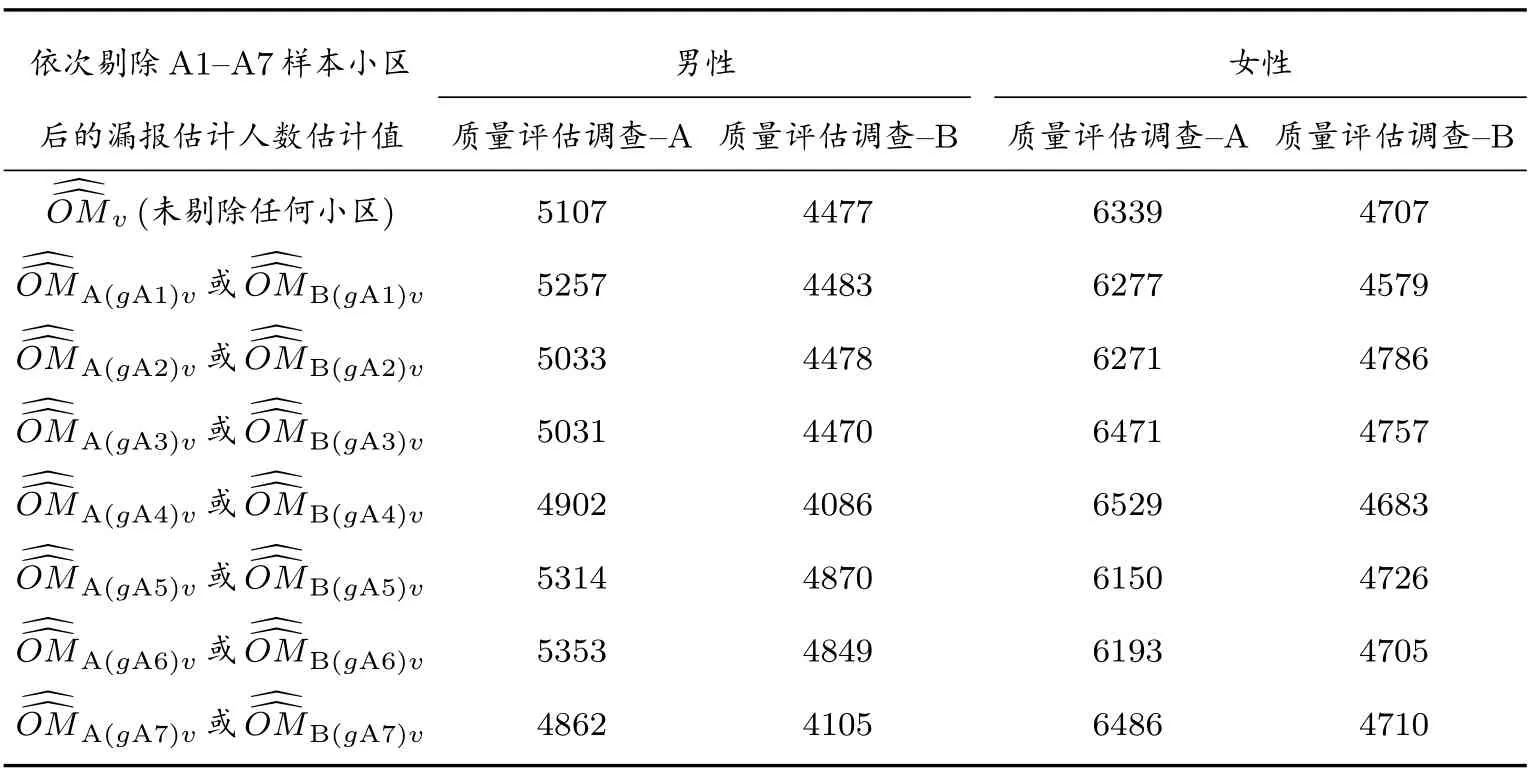
表11 普查漏報及復制漏報人數(人)

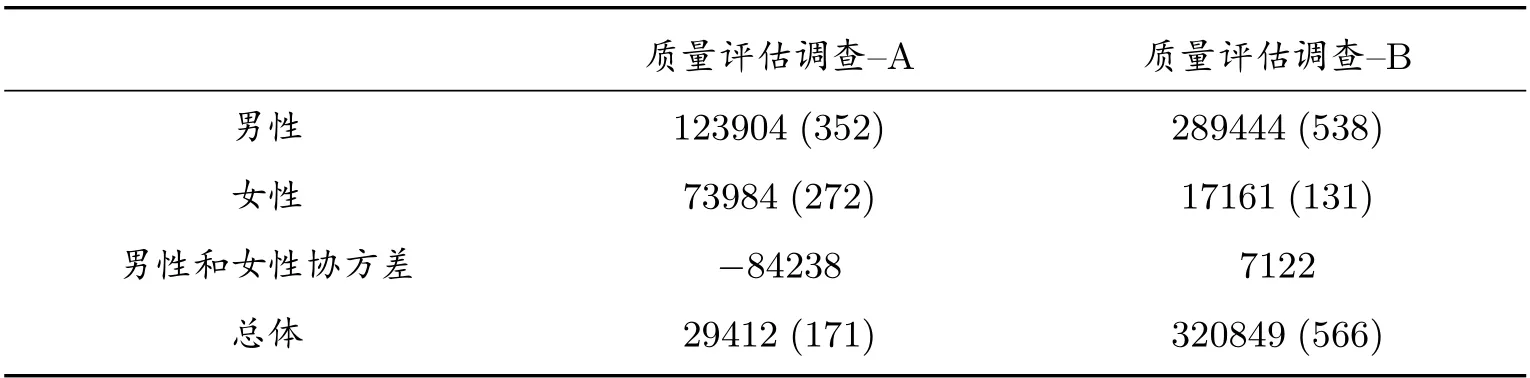
表12 抽樣誤差與協方差

表12 括號里面的數據為抽樣標準誤差.從表12 可以看出，采用質量評估調查-A，男性、女性和總體的抽樣標準誤差分別為352 人、272 人和171 人，即所估計的男性、女性和總體的普查漏報人數5107 人、6339 人和11446 人，與實際的男性、女性和總體的普查漏報人數平均相差352 人、272 人和171 人.采用質量評估調查-B，除女性外，男性和總體的抽樣標準誤差大一些.這說明，質量評估調查的人口構造方法對普查漏報估計的精度有影響.質量評估調查-A 使男性層和女性層呈負相關關系，協方差為負84238，降低普查漏報估計值的抽樣誤差，而質量評估調查-B 使男性層和女性層呈正相關關系，增加總體普查漏報估計值的抽樣誤差.因此，在普查漏報估計中，質量評估調查-A 提供精度更高的漏報估計值.

5.2 基于未匹配估計量的估計結果及數據分析

未匹配估計量，需要的樣本資料是普查人口名單、質量評估調查人口名單及其匹配人口名單，以及樣本普查小區的抽樣權數.樣本資料見表13 和表14.

使用表13 和表14 樣本數據，按照式(31)和(32)，以及式(33)-(36)，我們得到總體普查漏報估計值及抽樣方差.其中，質量評估調查-A 下的普查漏報估計值及抽樣標準誤差分別為9956 人和679 人，而質量評估調查-B 下的普查漏報估計值及抽樣標準誤差分別為8304 人和822 人.

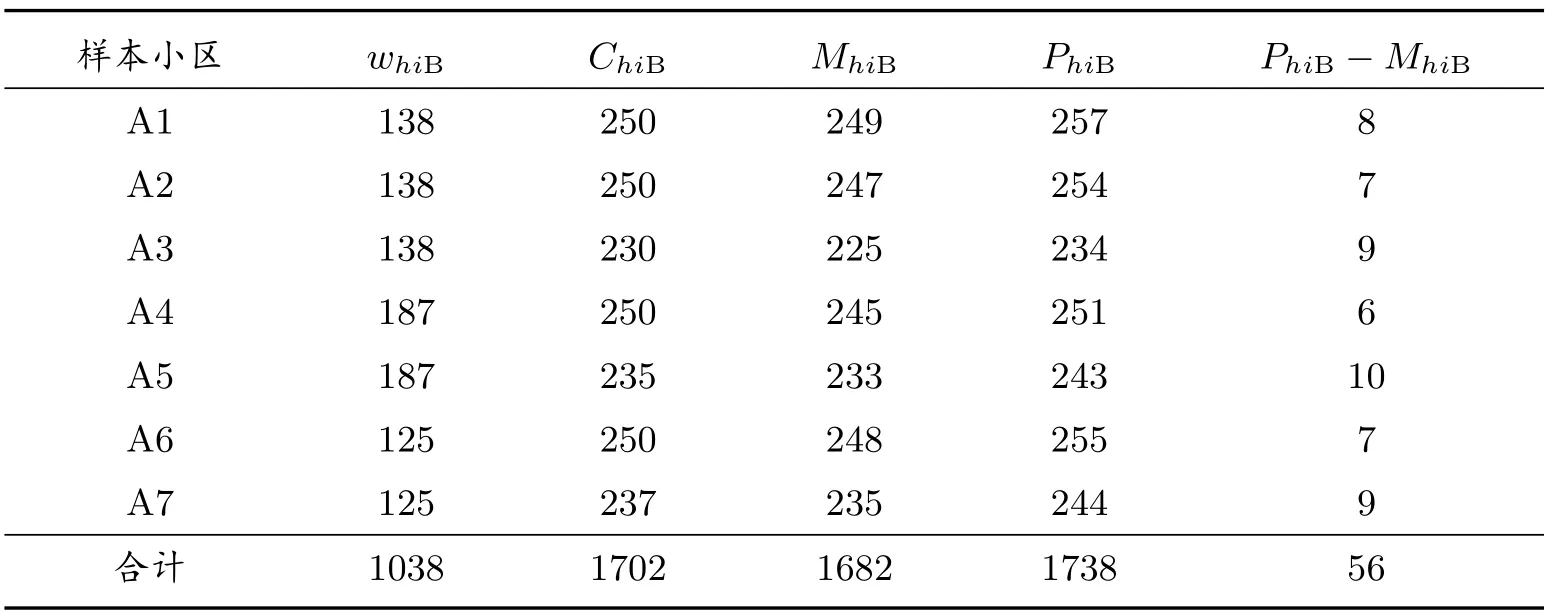
表14 質量評估調查-B 樣本普查小區人口資料(人)

5.3 普查漏報合成估計量與未匹配估計量的抽樣方差數據比較

在對比普查漏報合成估計量與未匹配估計量估計精度之前，首先把它們估計的結果列示在表15 中，然后根據表15 進行數據對比分析.

表15 兩種估計量的估計值(人)

在表15 中，從兩種普查漏報估計量的比對來看：采用質量評估調查-A，普查漏報合成估計量提供的漏報人數及抽樣標準誤差的估計值分別為11446 人和171 人，而未匹配估計量給出的相應估計值分別為9956 人和679 人；使用質量評估調查-B，普查漏報合成估計量提供的漏報人數及其抽樣標準誤差估計值分別為9184 人和566 人，而依據未匹配估計量得到的估計值分別為8304 人和822 人.這表明，一方面，不論采用質量評估調查-A，還是質量評估調查-B，普查漏報合成估計量的漏報估計值都大于未匹配估計量給出的漏報估計值.這與后者未包括同時被普查名單和質量評估調查名單遺漏的人口，而前者包括同時被三份名單漏報的人口有直接關系.這也是提出普查漏報合成估計量的原因之一；另一方面，在質量評估調查-A 和-B 兩種情況下，未匹配估計量的抽樣方差大于普查漏報合成估計量，說明后者的有效性強于前者.從對比質量評估調查-A 或-B 來看：無論是普查漏報合成估計量，還是未匹配估計量，采用質量評估調查-A，所得到的抽樣標準誤差估計值，比質量評估調查-B 的都要小一些.

6 結論與建議

第一，相比普查凈誤差估計及普查多報估計，普查漏報估計尚未受到各國政府統計部門及相關學者應有的重視.建議政府統計部門將凈誤差估計、多報估計及漏報估計放在同等重要的位置，加強漏報估計基礎理論研究，提高普查漏報估計精度.

第二，在判斷質量評估調查-A 還是B 哪個更優時，要同時考慮三個因素：是否對普查標準時點人口的追溯登記；資料的可得性；抽樣方差大小.質量評估調查-A 是對普查時點的追溯登記，符合人口普查質量評估的目標，抽樣方差較小，但獲取向外移動人口是否在普查時點登記有困難.只有在找到向外移動人口較容易的情況下，質量評估調查-A 才優于質量評估調查-B.建議政府統計部門在構造人口移動普查漏報合成估計量時，謹慎選擇質量評估調查-A 或B.

第三，現行普查漏報估計方法存在覆蓋漏報不全等缺陷.普查漏報合成估計量能夠規避這些缺陷.該估計量需要在等概率人口層建立.這需要確定對總體人口分層的變量.在每一層，先構造全面登記的普查漏報合成估計量，再依據有限總體概率樣本數據構造抽樣登記的普查漏報合成估計量.匯總所有等概率人口層的普查漏報合成估計量，得到省、自治區、直轄市以及全國的普查漏報合成估計量.建議政府統計部門在2020 年前后使用普查漏報合成估計量；研究三份名單不同統計關系的缺失單元漏報估計量；加強對總體人口分層變量選擇的研究，根據樣本規模確定最終分層變量及其數目和等概率人口層的層數，盡可能減少普查漏報估計值的抽樣誤差.

第四，普查漏報估計量替代現行普查漏報估計量是必然趨勢.首先，它包括了總體全部普查漏報人口.其次，它不受普查人口名單、質量評估調查人口名單和行政記錄人口名單是否獨立的限制.再次，它理論前沿.然而這種替代需要時間.建議政府統計部門與高校學者合作開展人口普查質量評估研究，尤其是前沿理論研究.