基于徑向基函數(shù)的自適應(yīng)網(wǎng)格方法

段獻(xiàn)葆， 黨 妍， 秦 玲

(西安理工大學(xué)理學(xué)院，西安 710048)

1 引言

許多物理和工程實(shí)際問題都可以用偏微分方程來描述，但是只有極少數(shù)的偏微分方程可以得到精確解，所以對于一般的偏微分方程，都是借助于數(shù)值方法求解.比較成熟的數(shù)值方法中大部分是依賴于網(wǎng)格的，如有限差分法、有限元法、有限體積等等.這些方法必須先生成網(wǎng)格后才能求解，網(wǎng)格質(zhì)量的好壞直接決定了最終數(shù)值求解的精度，而網(wǎng)格生成的預(yù)處理耗費(fèi)時間太大，在求解區(qū)域不規(guī)則或維數(shù)較高時，這些方法都有一定的困難.另一方面，在應(yīng)用這些方法求解大變形、斷裂問題或高維問題，特別是非定常問題，很多時候在求解的過程中都需要網(wǎng)格重構(gòu)，這大大地增加了計算量，也嚴(yán)重降低了數(shù)值解的精度[1，2].為了解決這些問題，自適應(yīng)網(wǎng)格方法是一個很好的選擇，國內(nèi)外許多學(xué)者在這方面進(jìn)行了大量地研究[3-6].

同樣是為了解決有限元方法等對網(wǎng)格依賴的問題，無網(wǎng)格方法近年來受到了很大的關(guān)注[7，8].這類方法試圖徹底地或部分地消除網(wǎng)格.相對于網(wǎng)格依賴的數(shù)值方法，無網(wǎng)格方法具有一些明顯的優(yōu)點(diǎn)，因此在其出現(xiàn)后得到了日益眾多的關(guān)注，并且一直是偏微分方程數(shù)值方法中的一個研究熱點(diǎn).一般說來，無網(wǎng)格方法基于一系列節(jié)點(diǎn)進(jìn)行函數(shù)插值，與有限元等網(wǎng)格依賴的方法相比，避免了網(wǎng)格劃分的預(yù)處理過程，也不會出現(xiàn)網(wǎng)格畸變的問題，對間斷問題、解的變化較大的問題等具有較好的優(yōu)勢.另一方面，無網(wǎng)格方法只需各個節(jié)點(diǎn)的獨(dú)立信息，而不需要單元之間的相互信息，數(shù)據(jù)結(jié)構(gòu)簡單.

利用徑向基函數(shù)(Radial Basis Function， RBF)求解偏微分方程的方法，是最近幾十年來備受關(guān)注的一類無網(wǎng)格方法[9].近年來，人們已經(jīng)用RBF 方法求解了各種線性和非線性的偏微分方程，并且取得了不錯的結(jié)果.其基本思想是在求解區(qū)域內(nèi)根據(jù)所求解的問題布置節(jié)點(diǎn)，然后在每個節(jié)點(diǎn)上構(gòu)造RBF，再將RBF 代入到所求解的偏微分方程，通過求解最終得到的代數(shù)方程獲得近似解.與網(wǎng)格依賴的方法不同，RBF 方法不需要任何網(wǎng)格，對支撐域和邊界沒有要求，只需要以節(jié)點(diǎn)為中心的子域覆蓋所求解區(qū)域即可.同時，RBF 與空間維數(shù)無關(guān)，僅依賴于節(jié)點(diǎn)間的距離，低維結(jié)果可以很容易推廣到高維問題.事實(shí)上，RBF 是通過定義在[0，+∞)上的一元函數(shù)φ 與Rd上的歐幾里德范數(shù)‖·‖來表示d 元函數(shù)φ(‖x-y‖)，其中x，y ∈Rd.因此用RBF 來處理多元問題具有效率高、儲存方便、運(yùn)算簡單的特點(diǎn).RBF 已廣泛應(yīng)用于計算幾何、微分方程數(shù)值解、神經(jīng)網(wǎng)絡(luò)等領(lǐng)域.近年來，國內(nèi)外學(xué)者對RBF 的理論與應(yīng)用進(jìn)行了系統(tǒng)的研究，隨著RBF 理論的逐漸發(fā)展，目前已成為求解偏微分方程的一個強(qiáng)有力的工具[10-15].但是RBF 方法的缺點(diǎn)也是顯而易見的，如理論方面很不完善，在逼近過程中所得到矩陣方程的系數(shù)矩陣是否可逆沒有相關(guān)理論結(jié)果，也即數(shù)值解的唯一性還沒解決；隨著中心節(jié)點(diǎn)增加，需要求解一個很大的方程組，并且這個方程組經(jīng)常是病態(tài)的；尚未見到開源或商業(yè)化的軟件，后處理以及所得結(jié)果與其他軟件的接口比較困難等等.為了解決這些問題，已經(jīng)有學(xué)者考慮自適應(yīng)的RBF 方法[16，17]，以及把有限元方法和RBF 方法相耦合的方法[18].

為了發(fā)揮無網(wǎng)格方法和網(wǎng)格依賴方法各自的優(yōu)勢，我們提出了一種基于徑向基函數(shù)的自適應(yīng)網(wǎng)格方法.利用有限元方法等數(shù)值結(jié)果結(jié)合徑向基函數(shù)方法在求解區(qū)域內(nèi)進(jìn)行自適應(yīng)配點(diǎn)，克服了有限元等方法計算中網(wǎng)格畸變和重新生成帶來的困難，所得結(jié)果可以用有限元等方法的后處理技術(shù)進(jìn)行分析.數(shù)值結(jié)果說明，所提方法產(chǎn)生的網(wǎng)格可以根據(jù)解的變化情況進(jìn)行網(wǎng)格自適應(yīng)，從而在保證相同數(shù)值求解精度的情況下可以極大地節(jié)省計算量.

2 徑向基函數(shù)

徑向基函數(shù)插值方法以其計算格式簡單、節(jié)點(diǎn)配置靈活、精度高的特點(diǎn)而成為研究多元逼近理論的有利工具，并已經(jīng)被應(yīng)用于科學(xué)計算模擬和實(shí)際工程問題中.

徑向函數(shù)滿足以下條件[19]：如果‖x1‖ = ‖x2‖，就有φ(x1) = φ(x2)的函數(shù)φ，也即，僅依賴r = ‖x‖的函數(shù)(其中‖·‖為Euclid 范數(shù)).RBF 就是這樣的函數(shù)空間：給定一個在定義域x ∈Rd上的一元函數(shù)φ:R+→R，所有形如Φ(x-c)=φ(‖x-c‖)及其線性組合張成的函數(shù)空間稱為由函數(shù)φ 導(dǎo)出的RBF 空間.在一定的條件下，只要取{xj}兩兩不同，{Φ(x-xj)}就是線性無關(guān)的從而形成徑向基函數(shù)空間中某子空間的一組基.當(dāng){xj}幾乎充滿R 時，{Φ(x-xj)}及其線性組合可以逼近幾乎任何函數(shù)[9].

1) Kriging 方法的Gauss 分布函數(shù)(無限光滑)：φ(r)=exp(-βr2)， β ＞0.

2) Duchon 的thin plate(薄板)樣條函數(shù)(分片光滑)：

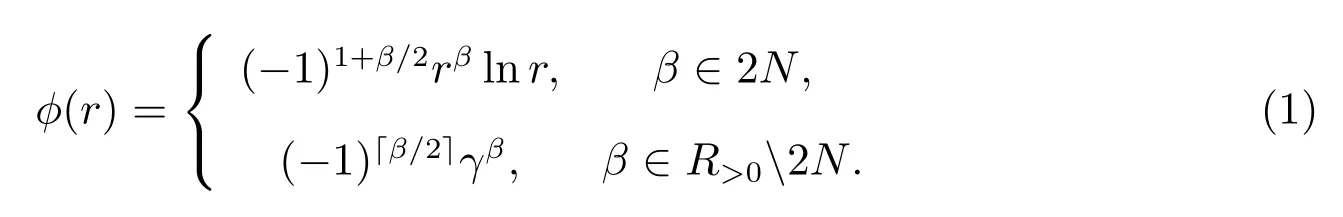
3) Sobolev 樣條函數(shù)：φ(r)=Kβ-d/2(r)rβ-d/2，其中K 為MacDonald 函數(shù).

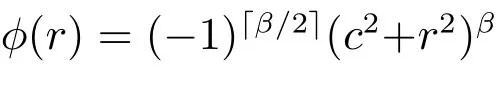
用RBF 求解偏微分方程的一般步驟如下：

對于偏微分方程

其中L 是偏微分算子，B 是邊界算子.在Ω 內(nèi)配置N 個離散的數(shù)據(jù)點(diǎn)r1，r2，··· ，rN，其中r1，r2，··· ，rl是內(nèi)部節(jié)點(diǎn)，而rl+1，rl+2，··· ，rN是邊界節(jié)點(diǎn).設(shè)方程(2)的解u 可以用RBF 表示為

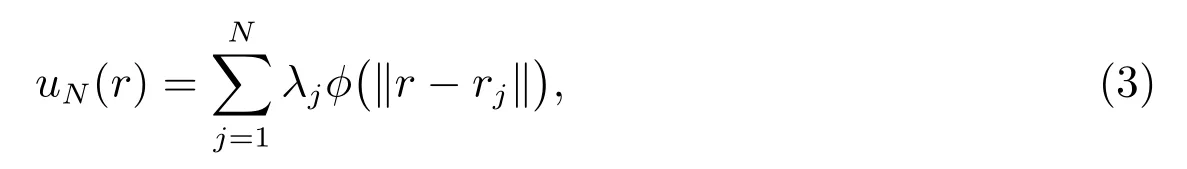
其中λ1，λ2，··· ，λN為待定系數(shù).由(2)式和(3)式可得

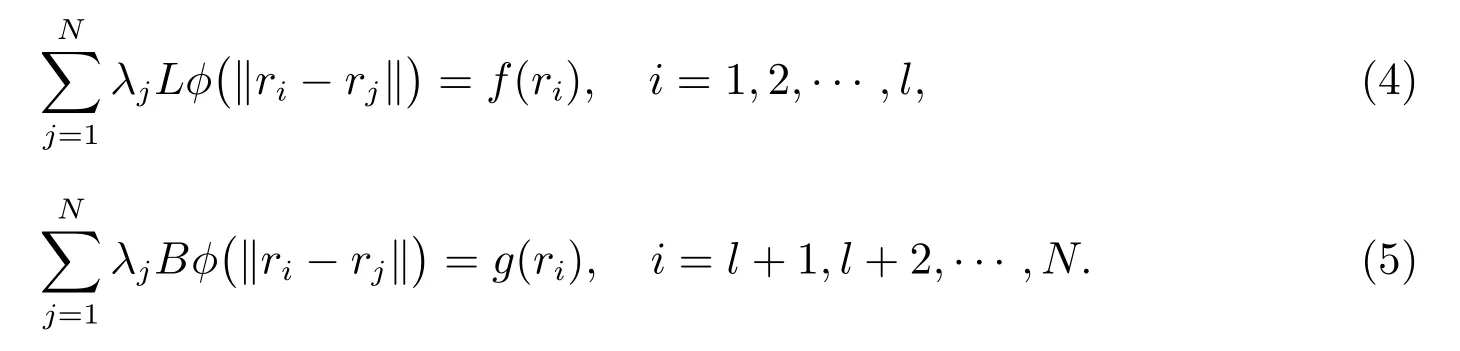
由(4)和(5)兩式得到矩陣方程

其中

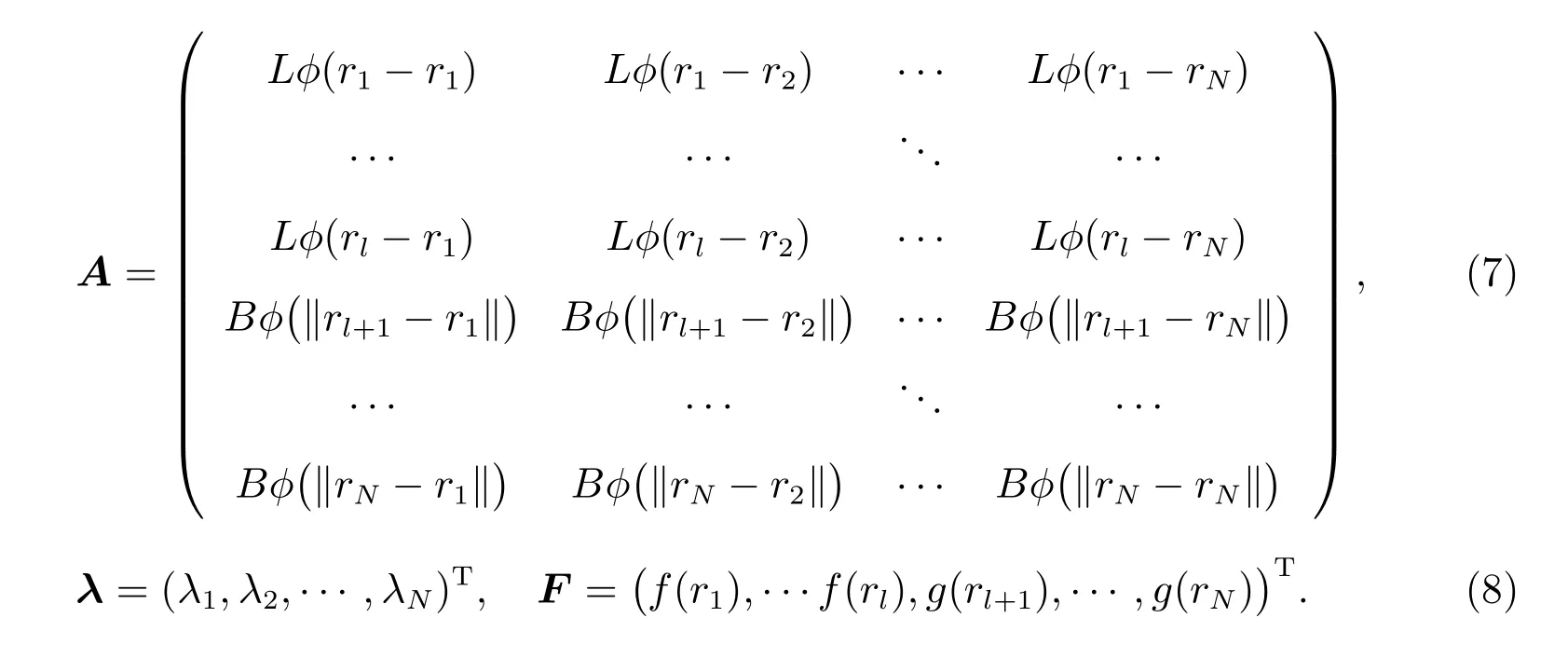
若矩陣A 是非奇異的，矩陣方程有唯一解，只要從(6)中解出λ，就可以得到方程(2)的近似解uN.

3 自適應(yīng)網(wǎng)格方法

最早由Berger 和Oliger 于1984 年提出的自適應(yīng)網(wǎng)格方法[20]，是一種高效且準(zhǔn)確的數(shù)值方法.該方法拋棄了等距均勻的網(wǎng)格，代之以能夠自動地適應(yīng)所研究問題中解的特征的疏密程度不均的網(wǎng)格.其網(wǎng)格結(jié)構(gòu)隨著計算過程的推進(jìn)而不斷的動態(tài)改變，根據(jù)計算的實(shí)際需要以及問題的特性改變計算區(qū)域內(nèi)的網(wǎng)格結(jié)構(gòu)，在物理量變化比較劇烈的地方，例如：大變形、激波面、接觸間斷面和滑移面等，采用空間尺度較小的精細(xì)網(wǎng)格，在物理量變化緩慢的地方則采用空間尺度較大的粗網(wǎng)格，這樣在保持計算高效率的同時得到高精度的數(shù)值解.

這一節(jié)我們給出一種簡單、易于實(shí)現(xiàn)的自適應(yīng)網(wǎng)格方法.該方法基于插值來調(diào)整RBF 的中心和參數(shù)，從而改變RBF 節(jié)點(diǎn)的分布.

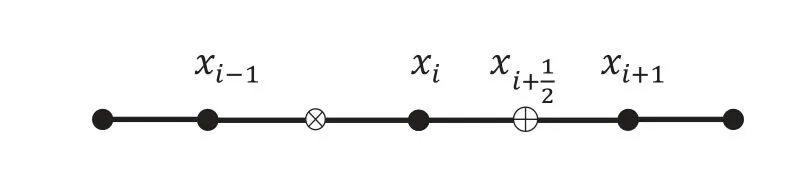
圖1 網(wǎng)格自適應(yīng)過程

對于二維問題來說，首先將求解區(qū)域進(jìn)行有限元分割，然后進(jìn)行有限元求解，與一維問題類似，用所得到的數(shù)值解可以求出方程(3)中的系數(shù)λi；接下來，可以用徑向基和λi得到每個初始單元的中點(diǎn)(重心)處的值，用這個值與有限元解在這點(diǎn)的插值得到誤差；誤差超過給定閾值的點(diǎn)將成為新的節(jié)點(diǎn)，并且利用這個節(jié)點(diǎn)把所在的單元進(jìn)行剖分；同樣，若誤差低于給定閾值，所在單元的節(jié)點(diǎn)都將被移除.

注1由于RBF 方法隨著節(jié)點(diǎn)的增加計算量會顯著上升，在誤差大于給定閾值的單元可以多細(xì)化幾次，但也不需要細(xì)化太多次.從我們的計算結(jié)果來看，細(xì)化兩次就可以達(dá)到非常理想的效果.

注2同一個節(jié)點(diǎn)可能會同時作為細(xì)化和粗化單元的節(jié)點(diǎn)，我們是先進(jìn)行細(xì)化，然后進(jìn)行粗化.

注3另一種可以采用的方法是一次增加多個節(jié)點(diǎn)，但在這個過程中會增加計算量，特別是RBF 方法.

注4這里給出的自適應(yīng)過程非常容易實(shí)施，并且可以推廣到更高的維度.

對于某些偏微分方程問題來說，如果初始節(jié)點(diǎn)不是太多，上述過程還可以簡化.如對于如下具有齊次Dirichlet 邊值的Poisson 問題

方程組(6)變?yōu)?/p>

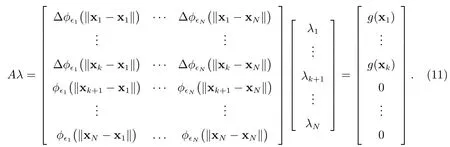
可以用RBF 方法直接求得系數(shù)λi.此時可以用如下公式

得到在節(jié)點(diǎn){y1，y2，...，yM}處的誤差，其中M 為RBF 的節(jié)點(diǎn)數(shù).

4 數(shù)值算例

本算例考慮Burgers 方程的求解問題.Burgers 方程是偏微分方程中的一個非常重要的方程，廣泛應(yīng)用于各個領(lǐng)域，如流體力學(xué)、非線性、氣體動力學(xué)、交通流等等.由于Burgers 方程是一個非線性方程，只有在很少的一些特殊情況下可以得到精確解，在更一般情形下，連數(shù)值求解都存在很大的困難.

我們考慮如下非定常Burgers 方程

其中Ω ?R2，?Ω 是Ω 的邊界，u =(u1，u2)是流體的速度.ν =1/Re(Re-Reynolds 數(shù))是粘性系數(shù)，f 表示體積力，g 為已知函數(shù).

設(shè)V =H1(Ω)2，則(13)-(15)的弱形式為：求u ∈V，使得

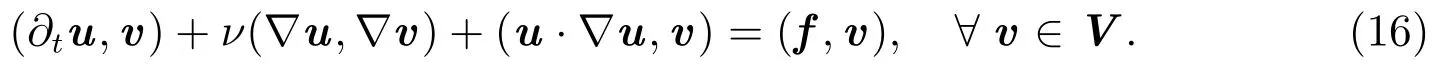
設(shè)Th是Ω 的一個三角剖分(h 是剖分參數(shù))，Vh是有限元空間，Vh?V，則(16)的有限元解為：求uh∈Vh，使得

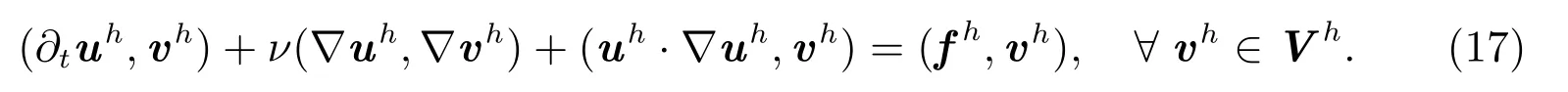
在下面的計算中，求解區(qū)域Ω=[0，1]×[0，1]， T =1，時間步長為Δt=0.01，

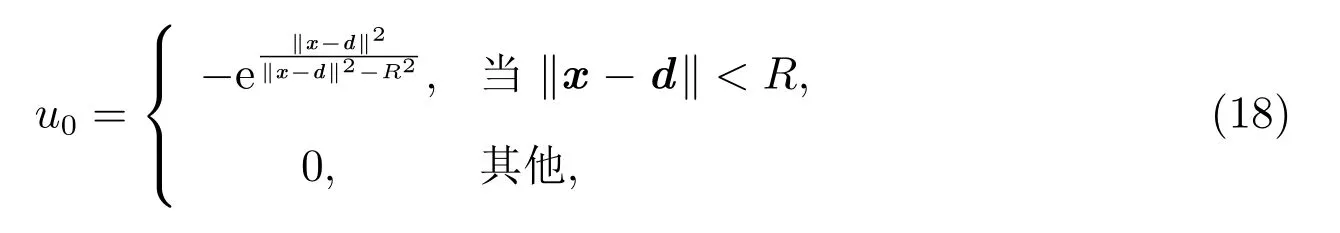
其中‖·‖表示歐氏范數(shù)，x =(x1，x2)， d =(0.3，0.3)， R=0.25.

本算例求解的過程中，當(dāng)誤差大于2×10-3時進(jìn)行網(wǎng)格細(xì)化，小于2×10-6時進(jìn)行網(wǎng)格粗化.粘性系數(shù)ν = 0.01.圖2 至圖4 分別給出了問題在時間t = 0， 0.5， 1 時的解.其中，圖2(a)、圖3(a)、圖4(a)為RBF 節(jié)點(diǎn)分布；圖2(b)、圖3(b)、圖4(b)為節(jié)點(diǎn)對應(yīng)的有限元網(wǎng)格；圖2(c)、圖3(c)、圖4(c)為網(wǎng)格對應(yīng)的有限元解.其中為了看得清楚，有限元解的圖片旋轉(zhuǎn)了一個角度.

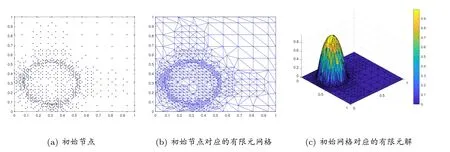
圖2 t=0 時的解

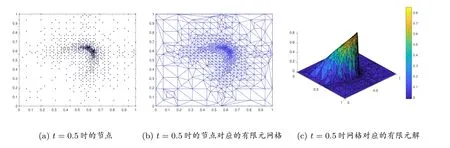
圖3 t=0.5 時的解

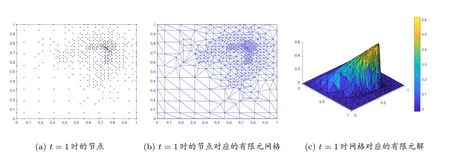
圖4 t=1 時的解

利用本文所提算法，在t = 0.5 時所用節(jié)點(diǎn)數(shù)和有限元網(wǎng)格單元數(shù)分別為656 個和1286 個，所用時間375.8368 秒.作為比較，我們用傳統(tǒng)有限元方法在t=0.5 時對本問題進(jìn)行了求解，所得結(jié)果如圖5 所示：用相同節(jié)點(diǎn)數(shù)的均勻(粗)網(wǎng)格對Burgers 方程進(jìn)行了求解，所得結(jié)果如圖5(a)所示，可以看出所得結(jié)果非常粗糙，根本無法接受；用均勻加密(細(xì))網(wǎng)格可以得到與圖3(c)接近精度的解，如圖5(b)所示，采用節(jié)點(diǎn)和有限元網(wǎng)格單元數(shù)分別為2704 個和5202 個，所用時間1184.7050 秒，大約是本文所提算法的3.15 倍.

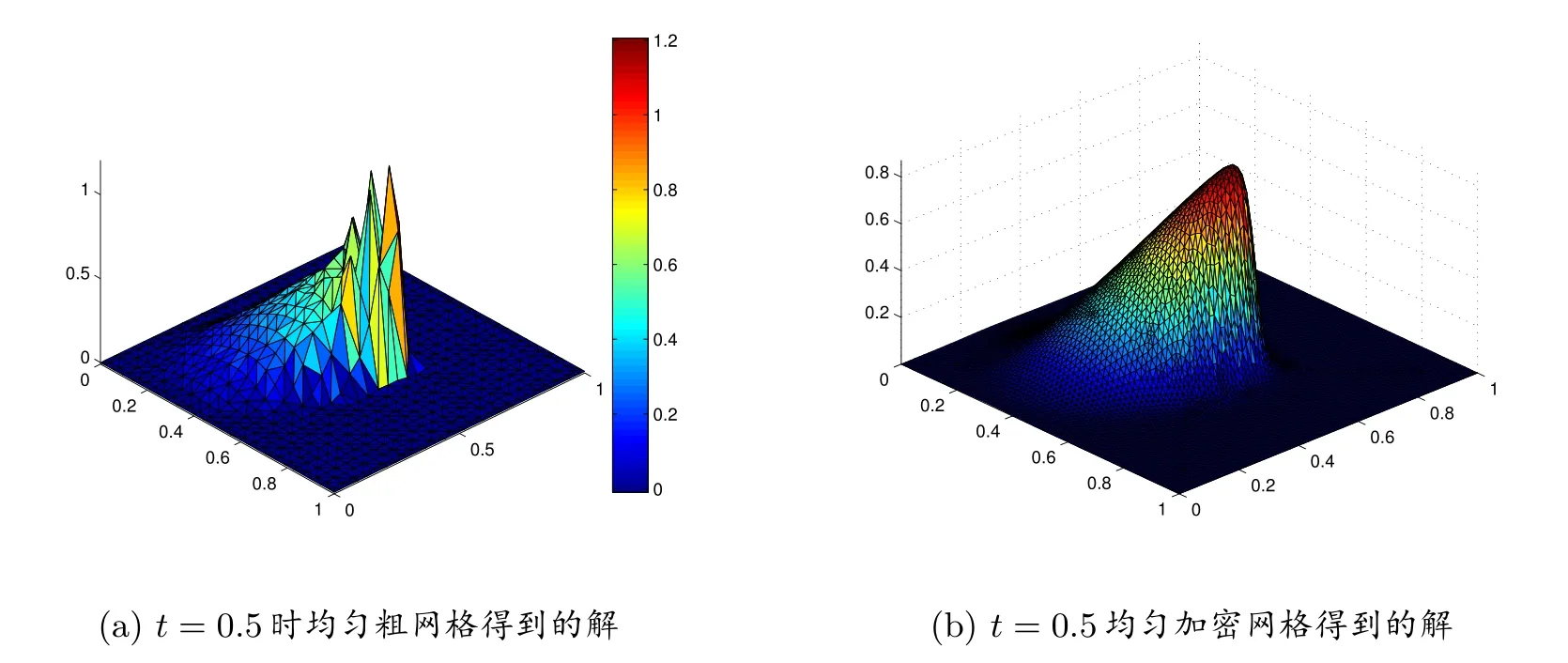
圖5 傳統(tǒng)有限元方法得到的解

從以上算例可以看出，本文所提算法可以在保持網(wǎng)格數(shù)量減少或不變的前提下較好的提高問題的求解精度，從而節(jié)省了求解時間.

5 結(jié)論

本文給出了一種求解偏微分方程的自適應(yīng)網(wǎng)格方法，該方法把徑向基函數(shù)計算格式簡單、節(jié)點(diǎn)配置靈活的優(yōu)點(diǎn)與網(wǎng)格依賴方法的穩(wěn)健性很好地結(jié)合起來.該算法非常容易實(shí)施.數(shù)值算例也表明所提算法可以在解變化劇烈的區(qū)域加密網(wǎng)格，而在解變化平緩的地方粗化網(wǎng)格，從而可以保持較高精度的前提下減少或不增加計算量.我們用非定常Burgers 問題對算法進(jìn)行的驗(yàn)證說明所提算法可以高效地求解偏微分方程問題.