數形結合百般好
——《點陣中的規律》教學實錄(一)
洪喬
【教學內容】
北師大版五年級上冊第98頁。
【教學過程】
一、計算比賽,激趣導入
師:先來做個小調查,咱們班誰計算速度最快?誰動作最快?
(選一位學生速算,再選一位學生用計算器計算,與教師比賽)
師:請看大屏幕中的題,任選其中一題進行比賽。其他同學看清楚了,你們是評委哦!

(比賽結果:教師獲勝)
師:想知道獲勝的秘訣嗎?
生:想。
師:老師把這道計算題轉化成了一個正方形點陣,只要用一句乘法口訣就能很快地算出答案,這種學習數學的方法叫做數形結合。(板書)
二、化難為易,獲得經驗
1.揭示數點數要找規律。(動畫依次呈現三角形點陣)

師:我們一起來數一數,這些圖形是由幾個點組成的?
生:第一個點陣是由1個點,第二個點陣由3個點,第三個點陣由6個點,第四個點陣由10個點,第五個點陣?第六個?第七個?
師:聲音怎么不整齊了?怎么回答不出來了?原來咱們還沒有發現其中的規律,今天我們就來學習點陣中的規律。(板書)
2.探索點陣內分組找規律的方法。
師:第三個點陣是怎么數的?
生:橫著數1+2+3=6。
生:斜著數也是1+2+3=6。
(學生回答的同時,教師用課件的熒光筆涂色,進行分組)
師:我們從上往下觀察這些點陣,你有什么發現?
生:從上往下看每個點陣,一層比一層多一個點。
師:我們再從左往右觀察每個點陣的算式,你又有什么發現?
生:從左往右看每個算式,后一個加數比前一個加數多一。
師:這些算式都是由點陣得到的,我們一起來說一說吧。
齊說:第一個點陣是1,第二個點陣是1+2,第三個點陣是1+2+3,第四個點陣是1+2+3+4,第五個點陣是1+2+3+4+5,……第N個點陣是1+2+3+……+N。
師:第七個點陣的算式應該從1一直加到幾?怎樣列式?
生:從1一直加到7,算式是1+2+3+4+5+6+7。
小結:對于這組三角形點陣,我們可以任取一個三角形采用分組的方法來研究,發現點陣中的規律是:一層比一層多一,那么相對應的算式中的規律是:從1開始,后面一個加數比前面一個加數依次多一,是第幾個點陣就加到幾。
三、自主探究,構建模型
師:請拿出學習卡。這是一組正方形點陣,請同桌兩人共同探索規律,寫出相應的算式,并說說點陣與算式之間的規律。

(同桌兩人運用所學知識,共同探討規律,教師巡視,手機拍照展示學生的探索結果)
1.橫著看,找規律。
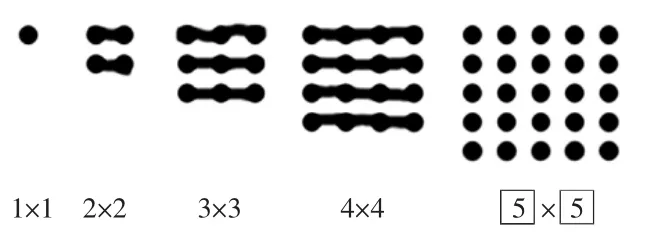
師:說說你是怎么找規律的?
生:我是橫著看找規律的,第一個點陣是1個1,所以列式1×1;第二個點陣是2個2,所以列式是2×2;第三個點陣是3個3,所以列式是3×3;第四個點陣是4個4,所以列式是4×4。
(課件同步演示:1×1,2×2,3×3,4×4)
師:那么第八個點陣的算式怎樣列呢?有多少個點?
生:8×8=64。
師:這個正方形點陣與算式之間有什么聯系嗎?
生:第一個點陣是1×1,第二個點陣是2×2,第三個點陣是3×3,第四個點陣是4×4……第N個點陣是N×N,第幾個點陣算式就是幾乘幾。
2.斜著看,找規律。
師:還有不同的方法嗎?
生:斜著看,找規律,第一個點陣是1,第二個點陣是1+2+1,第三個點陣是1+2+3+2+1,第四個點陣是1+2+3+4+3+2+1。(學生邊說教師邊同步出示算式)
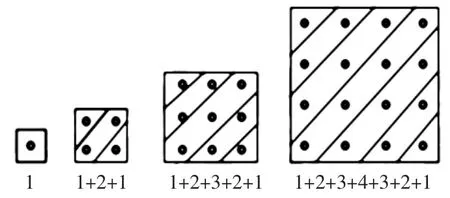
師:仔細觀察第三個點陣,我們把正方形沿對角線分成了兩個三角形,就成了我們之前研究的三角形點陣,誰知道正方形的這條對角線的點數對應在算式里的什么數嗎?
生:對應算式里的3。
師:誰能說說點陣與算式之間的規律?
生:點陣中的點數依次多一,然后又依次減一。相對應的算式也是依次加一,然后又依次減一。
師:還有不同的發現嗎?
生:第二個點陣最大數是2,第三個點陣最大數是3,第四個點陣最大數是4……那么第N個點陣最大加數就是N。
師:誰能說說第五個點陣相對應的算式嗎?
生:1+2+3+4+5+4+3+2+1。
3.拐彎看,找規律。
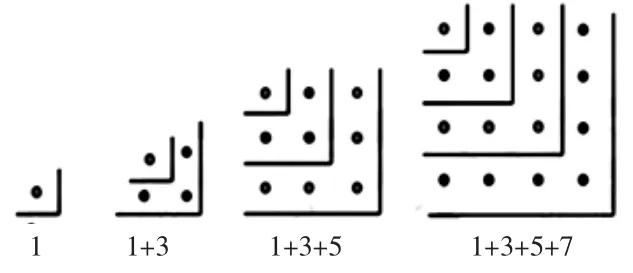
師:這組正方形點陣,你還能列出不一樣的分組方法嗎?
(展示學生拐彎分的涂色方法,并課件動畫出示1個點、3個點、5個點、7個點,最后組成了正方形點陣)
師:你會根據這種分法列出相應的算式嗎?
生:第二個算式是1+3,第三個算式是1+3+5,第四個算式是1+3+5+7。
師:你發現算式中各數有什么特點嗎?
生:是一組連續奇數的和。
師:再觀察點陣與算式之間有什么規律嗎?(如果學生發現不了,可以啟發:圖形被折線分成了幾組?所以算式中就有幾個數?)
生:第二個點陣被分成了2組,所以算式中有2個數相加。第三個點陣被分成了3組,所以算式中有3個數相加。第四個點陣被分成了4組,所以算式中有4個數相加。
師:第N個點陣,就是從1開始的N個連續奇數相加。
師:剛才我們是在同一個點陣內找規律的。我們還可以與前一個點陣比較來看,還有其他找規律的方法嗎?
生:發現第二個點陣比前面一個點陣新增了3個點,所以在前一個點陣的算式后面加3。第三個點陣比前面的點陣新增了5個點,所以在前一個點陣的算式后面加5。第四個點陣比前面一個點陣新增了7個點,所以在前一個點陣的算式后面加7。
師:原來我們橫向比較也能發現規律,列出相對應的算式。現在老師要來考考你們了,第五個點陣相對應的算式誰會列?
生:1+3+5+7+9。
四、揭示秘訣,固化新知
1.探索三個算式間的聯系。
師:(結合板書)橫著看,列式是4×4;斜著看,列式是1+2+3+4+3+2+1;拐彎看,列式是1+3+5+7,結果都是多少?為什么?
生:16,都是同一個點陣。
生:把后兩個算式通過移多補少或重新配對可變成4個4。
師:這三種方法中,你最喜歡哪種分法?為什么?
生:第一種,計算最簡便。
2.揭示比賽獲勝秘訣。
師:這些算式都是同一個正方形點陣,所以在計算時,老師把這些算式都轉化成了正方形的第一種分法,直接用乘法口訣4×4=16,就很快算出答案了。你現在知道前面人機大戰老師獲勝的秘訣了嗎?
生:老師都是看算式想是幾乘幾的點陣,是幾乘幾的點陣就用幾乘幾算出結果。
師:大家說一說人機大戰中六個算式各是幾乘幾的點陣?
3.小結。
師:原來數形結合可以這么巧妙地解決數學問題,難怪中國現代“數學之父”華羅庚用他樸素的語言作了一首七言絕句。(課件展示)

五、延伸應用,形成策略
1.我們來看一看這道題:比一比,看誰算得又對又快。
課件出示:
(1)1+2+3+……+20+……+3+2+1
生:都等于20×20=400。
師:看到這樣的算式,你能想到什么樣的點陣呢?
生:一排20個點,共有20排。
2.請按長方形點陣中的規律填空。

六、聯系生活,結課欣賞
1.欣賞圖片。

2.請你設計一個點陣,看你的爸爸、媽媽或同學能不能找出你設計的規律?

