“數形結合”探秘絕對值

文張文珠

著名數學家華羅庚先生曾經說過：“數缺形時少直觀，形少數時難入微；數形結合百般好，隔離分家萬事休。”對絕對值的探究過程，“數軸”充當了橋梁的作用。絕對值借助數軸來表達，充分體現了數學中“數形結合”的思想精髓。接下來，讓我們開始一場絕對值的探秘之旅。

一、整裝待發——理解絕對值的幾何意義

數軸上表示一個數的點與原點的距離，叫做這個數的絕對值。

“數a 的絕對值”記作 ||a ，幾何意義為數軸上表示數a的點與原點的距離。

例1如圖1，| |-3 的幾何意義為數軸上表示-3的點與原點的距離。

圖1

二、腳踏實地——探秘任務一：兩數差的絕對值

“兩數差的絕對值”記作|a - b|（a、b是常數），幾何意義為數軸上表示數a 和數b 的兩個點之間的距離。

例2如圖2，|5- 2| 表示5 與2 的差的絕對值，實際上可以理解為5與2兩數在數軸上所對應的兩點之間的距離；由計算可得|5- 2|=3；由數軸可得5 與2 兩數在數軸上所對應的兩點之間的距離是3，所以|5- 2 |=3。

圖2

如圖3，|5+2|即|5-（-2）|，表示5 與-2的差的絕對值，實際上可以理解為5 與-2 兩數在數軸上所對應的兩點之間的距離。由計算可得|5+ 2 |=7；由數軸可得5 與-2 兩數在數軸上所對應的兩點之間的距離是7，所以|5+2|=7。

圖3

經驗升級：用數學語言表示“兩數差的絕對值”，兩數之間要用運算符號“-”號連接，若遇到兩數之間用“+”號連接，需要轉化為“-”號。

三、登高望遠——探秘任務二：兩距離之和的最小值

“兩距離之和”記作|x-a|+|x-b（|x 是未知數，a、b 是常數），可以理解為數軸上表示x 的點（動點）分別與表示a、b 的點（定點）之間的距離之和。

例3求|x+1|+|x-5|的最小值。

【解析】原式寫成兩數差的絕對值為|x-（-1）|+|x-5 |，可以理解為數軸上表示x的點（動點）分別與表示-1、5 的點（定點）之間的距離之和。因為x 的不確定性，可以利用數軸畫出表示-1、5 的兩個定點，然后分類討論如下：

1.表示數x 的點在表示-1 的點左側，兩距離長如圖4所示：

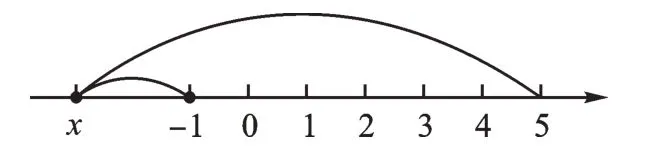
圖4

2.表示數x 的點在表示-1 和5 的兩點之間（包括兩點），兩距離長如圖5所示：

圖5

3.表示數x 的點在表示5 的點右側，兩距離長如圖6所示：

圖6

由圖可知，當數軸上表示數x 的點位于表示數-1 和5（包括-1 和5）兩點之間時，|x+1 |+|x - 5 |取得最小值，最小值就是表示數-1和5 兩點之間的距離（|-1）- 5 |=6（見“探秘任務一”所得結論）。所以|x + 1 |+|x - 5 |的最小值是6。

經驗升級：求兩距離之和的最小值，首先將原式寫成兩數差的絕對值；其次理解式子的幾何意義，借助數軸畫出定點；最后利用數形結合對動點的不同位置分類討論，得出最短距離和即為所求最小值。

四、手摘星辰——探秘任務三：多個距離之和最小值

“多個距離之和”記作|x - a1|+|x - a2|+…+|x -an（|x 是未知數，a1、a2、……、an是常數），可以理解為數軸上表示x 的點（動點）分別與表示a1、a2、……、an的點（定點）之間的距離之和。

例4求|x - 1 |+|x + 2 |+|x - 3 |的最小值。

【解析】原式寫成兩數差的絕對值為|x - 1 |+|x -（-2）|+|x - 3 |，可以理解為數軸上表示x的點（動點）分別與表示1、-2、3的點（定點）之間的距離之和。如圖7，因為x 的不確定性，可以利用數軸畫出表示1、-2、3 的三個定點，然后分類討論，可得：當x=1 時，|x - 1|+|x + 2 |+|x - 3 |的最小值是5。

圖7

例5求|x- 1 |+|x + 2 |+|x - 3 |+|x + 4 |的最小值。

【解析】數形結合分類討論后，如圖8 從數軸上可以看出最小值就是表示數-2和1兩點之間的距離與表示數-4和3兩點之間的距離之和，記作|-2 - 1 |+|-4 - 3 |=10。所以，當x 在-2 與1 之間（包括-2 和1）時，|x - 1 |+|x + 2 |+|x - 3 |+|x + 4 |的最小值是10。

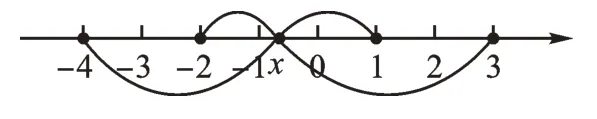
圖8

經驗升級：若數軸上有奇數個定點，則當動點在最中間的定點時，原式有最小值，再借助數軸求出最小值；若數軸上有偶數個定點，則當動點在最中間兩個定點之間（包括這兩點）時，原式有最小值，再借助數軸求出最小值。

在這場絕對值的探秘之旅過程中，“數軸”功不可沒，它帶領我們把一個非常抽象的問題進行了直觀展示，幫助我們理解了“絕對值”的本質，數形結合貫穿于整個探秘之旅中。絕對值的探秘之旅告一段落，前方還有更加精彩的數學世界等著同學們去探索。