玻璃鋼板的振動特性研究

陳 哲

(鄭州機(jī)電工程研究所 第一研究室，河南 鄭州 450015)

0 引言

纖維增強(qiáng)樹脂基復(fù)合材料質(zhì)量輕、耐腐蝕、可設(shè)計(jì)性強(qiáng)、比強(qiáng)度高，其在艦艇等工業(yè)領(lǐng)域正逐漸代替?zhèn)鹘y(tǒng)材料。英國的“威爾遜”號掃雷艇、“亞賓吉-21”號摩托艇都采用玻璃鋼作為主體材料，俄羅斯AK-630型艦炮、美國MK42型艦炮均采用玻璃鋼作為炮塔的材料，輕量化效果顯著。與傳統(tǒng)金屬材料相比，纖維樹脂基復(fù)合材料既能保證結(jié)構(gòu)的承載能力，又能有效地提高結(jié)構(gòu)的阻尼性能，對振動控制具有十分重要的意義。國內(nèi)外學(xué)者針對玻璃鋼的振動特性開展了一系列研究，徐寧等[1]采用實(shí)驗(yàn)方法研究了纖維用量和纖維排布方式對玻璃鋼板的輻射效率和損耗因子的影響；武海鵬等[2]通過實(shí)驗(yàn)分別測試了纖維體積含量為60%的玻璃纖維和碳纖維復(fù)合材料的阻尼，發(fā)現(xiàn)單層纖維的角度對阻尼性能影響顯著；史盼等[3]以約束阻尼復(fù)合結(jié)構(gòu)為研究對象，采用動態(tài)黏彈譜儀和懸臂梁共振法研究了它的阻尼特性，發(fā)現(xiàn)采用玻璃鋼作為約束層可以把復(fù)合結(jié)構(gòu)的高阻尼性能拓展至寬頻域和寬溫域；賈寶惠等[4]通過理論推導(dǎo)與有限元仿真，探究了溫度和濕度對正交各向異性復(fù)合材料層合板振動特性的影響；Lee S K等[5]采用試驗(yàn)方法研究了碳纖維鋪層方向?qū)μ祭w維-環(huán)氧樹脂基層合板振動性能的影響，研究發(fā)現(xiàn)可以通過改變纖維鋪設(shè)角度來控制聲壓級；漆文凱等[6]采用多點(diǎn)激勵(lì)、單點(diǎn)拾振的模態(tài)測試方法，分別對無損傷和有開孔損傷工況下的復(fù)合材料層合板進(jìn)行自由振動和強(qiáng)迫振動測試，研究發(fā)現(xiàn)，開孔損傷的位置和大小對復(fù)合材料層合板的振動特性影響顯著；Landge A D[7]采用有限元方法研究了具有不同類型材料配置和纖維角度的層合板的自由振動與強(qiáng)迫振動。然而，針對玻璃鋼板的振動研究還不充分，尚不能滿足工程應(yīng)用的需要。

為了更加準(zhǔn)確地預(yù)報(bào)玻璃鋼復(fù)合材料層合板整體的振動特性，本文借鑒Matter等[8-9]提出的修正復(fù)合材料基本動態(tài)力學(xué)參數(shù)的方法，結(jié)合試驗(yàn)和仿真來確定單向玻璃纖維鋪層的基本動態(tài)力學(xué)性能：首先對玻璃鋼層合板進(jìn)行模態(tài)試驗(yàn)，獲得其各階模態(tài)振型、固有頻率和阻尼比；然后建立玻璃鋼層合板的有限元模型，并代入材料參數(shù)初始值進(jìn)行仿真分析，對比分析試驗(yàn)和數(shù)值仿真的結(jié)果，在保證試驗(yàn)和仿真得到的各階模態(tài)振型一致的前提下，通過不斷迭代優(yōu)化有限元模型的相關(guān)參數(shù)，使有限元仿真結(jié)果不斷趨近于模態(tài)測試獲得的各階固有頻率，直至滿足精度要求。

1 模態(tài)試驗(yàn)

試驗(yàn)?zāi)Ｐ蜑椴Ａт搶雍习澹亴硬捎脝蜗虿ＡЮw維增強(qiáng)復(fù)合材料，單層表現(xiàn)為正交各向異性。玻璃鋼層合板的幾何參數(shù)為900 mm×900 mm×6 mm。對模型進(jìn)行自由振動測試，獲得模型的模態(tài)參數(shù)，為玻璃鋼層合板模型參數(shù)的修正奠定基礎(chǔ)。經(jīng)反復(fù)迭代修正后的單向玻璃纖維鋪層材料參數(shù)如表1所示，其中，E1、E2為材料在兩個(gè)主方向上的彈性模量，G12、G13、G23為在三個(gè)平面內(nèi)的剪切模量，υ12、υ13、υ23為在三個(gè)平面內(nèi)的泊松比。

表1 單向玻璃纖維鋪層材料參數(shù)

圖1為模態(tài)試驗(yàn)裝置。模型按照6×6等分，對每個(gè)節(jié)點(diǎn)進(jìn)行編號，從左至右每一列編號依次為1～7、8～14、…、43～49。模態(tài)測試采用柔性繩懸掛法近似等效自由邊界條件，加速度傳感器的固定方式為石蠟粘合，模態(tài)辨識方法為多點(diǎn)激勵(lì)、單點(diǎn)拾振，通過力錘敲擊測試模型，敲擊5次取平均得到其頻響函數(shù)，根據(jù)頻響函數(shù)辨識出各階固有頻率和模態(tài)振型。

圖1 模態(tài)試驗(yàn)裝置

2 試驗(yàn)結(jié)果

此處為了表達(dá)清晰和方便比較，只給出了結(jié)構(gòu)前3階彎曲模態(tài)。模態(tài)試驗(yàn)和有限元模擬得到的玻璃鋼板前3階彎曲模態(tài)對比分別如圖2～圖4所示。試驗(yàn)獲得的玻璃鋼板前3階彎曲模態(tài)固有頻率和阻尼損耗因子如表2所示。試驗(yàn)和仿真得到的玻璃鋼板前3階彎曲模態(tài)固有頻率對比如表3所示。

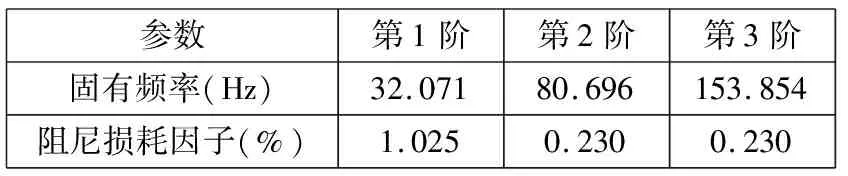
表2 試驗(yàn)得到的玻璃鋼板前3階固有頻率和阻尼損耗因子

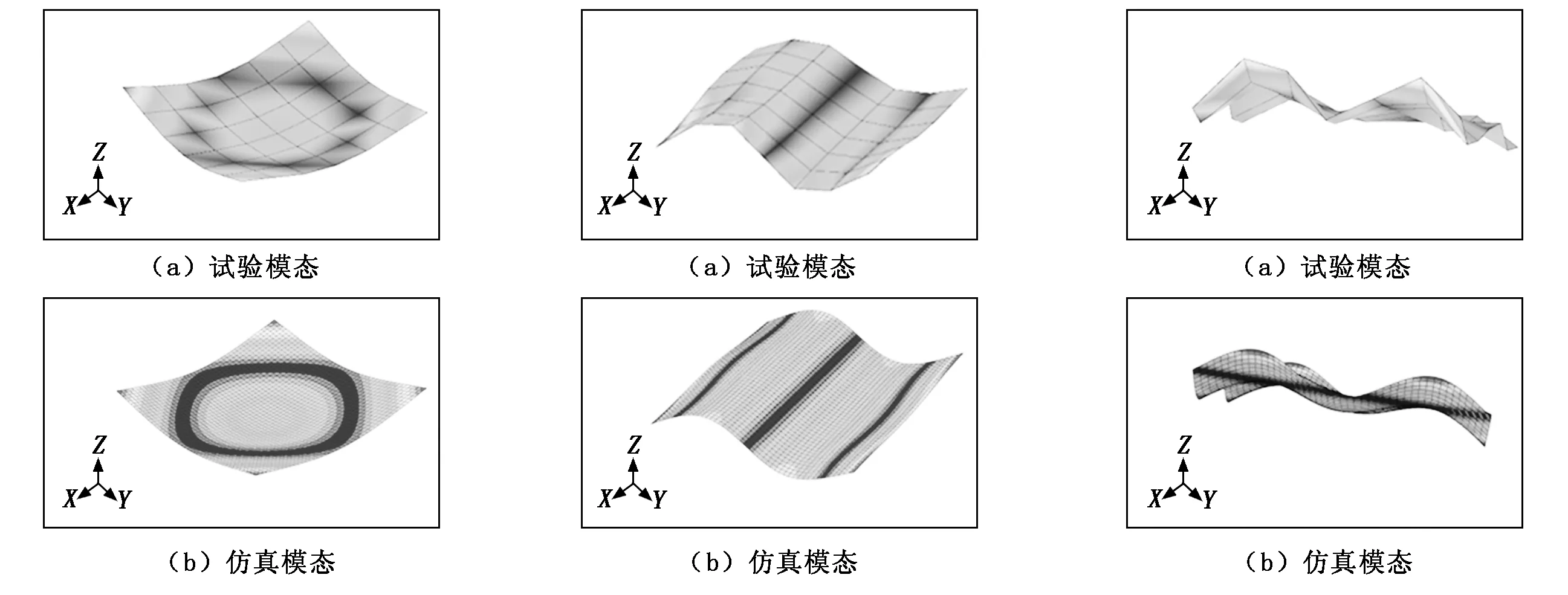
圖2 玻璃鋼板的1階彎曲模態(tài)對比 圖3 玻璃鋼板的2階彎曲模態(tài)對比 圖4 玻璃鋼板的3階彎曲模態(tài)對比

從表3可以看出：采用迭代方法修正后的有限元模型進(jìn)行仿真，得到的固有頻率與試驗(yàn)結(jié)果的誤差最大不超過3.9%，滿足精度要求，說明建立的玻璃鋼復(fù)合材料板的有限元模型可靠。經(jīng)分析，誤差產(chǎn)生的原因主要是有限元建模時(shí)忽視了真實(shí)模型的殘余應(yīng)力、界面缺陷以及局部纖維不規(guī)則排列(如圖5所示)等因素。

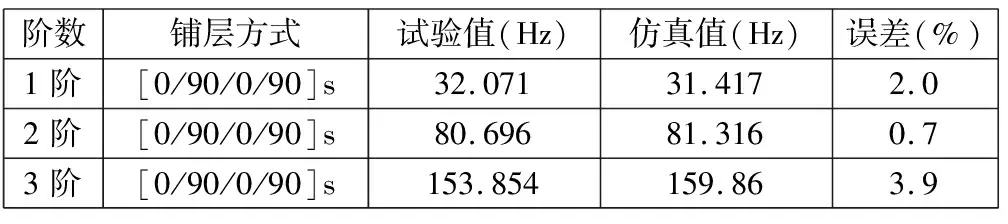
表3 玻璃鋼板前3階固有頻率試驗(yàn)和仿真結(jié)果對比

圖5 玻璃纖維局部排列不規(guī)則

3 仿真分析

采用有限元軟件ABAQUS建立玻璃鋼層合板的數(shù)值計(jì)算模型。雖然模型在幾何上是薄板，但是玻璃鋼板的剪切模量相對較低，橫向剪切變形不可忽略，所以為了在提高計(jì)算精度的同時(shí)降低計(jì)算量，本文模型采用模擬厚殼問題的Shell S4R單元。模型主要參數(shù)如下：正方形玻璃鋼板邊長L=0.9 m，厚度為6 mm；激勵(lì)力作用在中心(x/2，y/2)處，幅值為1 N；測量頻率f=1 000 Hz；邊界條件為四邊自由；空氣中聲速c=340 m/s，空氣密度ρ空=1.225 kg/m3。

3.1 交替鋪層角度改變對玻璃鋼板振動性能的影響

對于纖維增強(qiáng)復(fù)合材料來說，在對纖維層的鋪層角度設(shè)計(jì)時(shí)，為了避免纖維層合結(jié)構(gòu)出現(xiàn)分層破壞，相鄰鋪層應(yīng)盡量避免出現(xiàn)相同的鋪層角度。此處選取±15°、±30°、±45°三種交替角度對玻璃鋼板進(jìn)行鋪層，每層厚度為0.3 mm，總層數(shù)為20層，模態(tài)試驗(yàn)修正后的模型材料參數(shù)如表1所示。

圖6為3種交替鋪層角度下玻璃鋼板的振動頻響曲線。從圖6中可以看出：在中低頻段(0 Hz～800 Hz)，±15°和±45°兩種鋪層角度下的均方振速除峰值外大致重合，而且低于±30°角度下的情況；800 Hz～1 000 Hz頻段內(nèi)，±45°鋪層角度的均方振速低于另外兩種鋪層角度。因此在進(jìn)行鋪層設(shè)計(jì)時(shí)，可以適當(dāng)增大±45°鋪層角的鋪層比例。

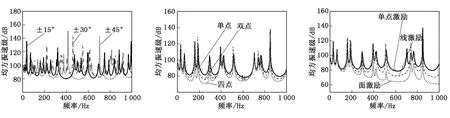
圖6 3種交替鋪層角度下玻璃鋼板的振動性能曲線 圖7 多點(diǎn)激勵(lì)對玻璃鋼板振動性能的影響 圖8 力的分布形式對玻璃鋼板振動性能的影響

3.2 力激勵(lì)的分布形式對玻璃鋼板振動性能的影響

船舶的動力裝置是船舶主要的噪聲源之一，動力裝置主要通過基座與船體相連，與基座的連接方式主要有點(diǎn)連接、線連接和面連接等。對于同樣的振源設(shè)備，采用不同安裝方式會導(dǎo)致不同的振動響應(yīng)，工程中常需要選擇使結(jié)構(gòu)振動響應(yīng)最小的安裝方式。因此，本文分析了力激勵(lì)的不同分布形式對玻璃鋼板振動性能的影響。

3.2.1 多點(diǎn)激勵(lì)對玻璃鋼板振動性能的影響

力的激勵(lì)個(gè)數(shù)及位置如下：

(1)單點(diǎn)：在(L/2,L/2)處施加幅值為1 N的簡諧力。

(2)雙點(diǎn)：在(L/3,L/2)和(2L/3,L/2)處各施加幅值為0.5 N的簡諧力。

(3)四點(diǎn)：在(L/3,2L/3)、(L/3,L/3)、(2L/3,L/3)、(2L/3,2L/3)處各施加0.25 N的簡諧力。

圖7為激勵(lì)點(diǎn)個(gè)數(shù)對玻璃鋼板振動性能的影響。由圖7可知：隨著激勵(lì)力個(gè)數(shù)的增加，玻璃鋼板的均方振速明顯降低。

3.2.2 點(diǎn)力激勵(lì)、線力激勵(lì)和面力激勵(lì)對玻璃鋼板振動性能的影響

分別選擇單點(diǎn)激勵(lì)、線力激勵(lì)和面力激勵(lì)進(jìn)行比較，探究3種激勵(lì)力對玻璃鋼板振動的影響。力的分布形式及位置如下：

(1)單點(diǎn)激勵(lì)：在(L/2,L/2)處施加幅值為1 N的簡諧力。

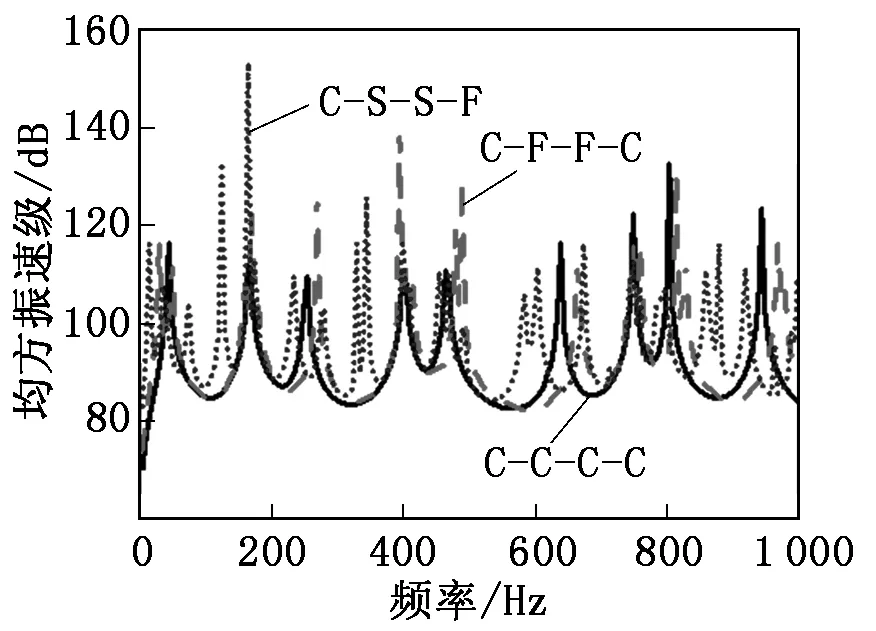
(2)線力激勵(lì)：在(L/3

(3)面力激勵(lì)：在(L/3

圖8為力的分布形式對玻璃鋼板振動性能的影響。由圖8可知：在低頻段，玻璃鋼板的均方振速頻響曲線在3種激勵(lì)方式下非常接近;在中高頻段，單點(diǎn)激勵(lì)下的均方振速最大，面激勵(lì)下的均方振速最低。由此可見，在工程應(yīng)用中可以通過增大振源和玻璃鋼板的接觸面積來降低玻璃鋼板的振動響應(yīng)。

3.3 一般邊界條件對玻璃鋼板振動性能的影響

實(shí)際工程中，結(jié)構(gòu)的邊界條件通常比較復(fù)雜，不僅是典型邊界條件如四邊簡支(S-S-S-S)、四邊固支(C-C-C-C)、自由(F-F-F-F)等，還有可能是幾種形式的組合,因此有必要探究非典型邊界條件下玻璃鋼層合板的振動特性。

圖9為不同邊界條件對玻璃鋼板振動性能的影響。從圖9可以看出：邊界條件對玻璃鋼層合板的振動特性影響顯著，對比不同邊界條件下的均方振速曲線發(fā)現(xiàn)，C-S-S-F邊界條件下的共振峰最密集，C-F-F-C邊界條件下的共振峰次之，C-C-C-C邊界條件下的共振峰數(shù)量最少。由此可知：隨著邊界約束條件的增強(qiáng)，玻璃鋼層合板振動曲線的共振峰數(shù)量減少，輻射能量也減小。因此，在工程實(shí)際中可通過增強(qiáng)層合板結(jié)構(gòu)的邊界約束條件來降低其振動水平。

圖9 不同邊界條件對玻璃鋼板振動的影響

4 結(jié)論

本文以玻璃鋼板為研究對象，基于模態(tài)試驗(yàn)對玻璃鋼板的參數(shù)進(jìn)行修正，采用有限元方法實(shí)現(xiàn)了復(fù)合材料層合板結(jié)構(gòu)的振動特性預(yù)報(bào)。在驗(yàn)證玻璃鋼復(fù)合材料板模型有效性的基礎(chǔ)上，探究了纖維層鋪設(shè)角度、力激勵(lì)的不同分布形式和一般邊界條件對玻璃鋼板振動特性的影響規(guī)律。研究結(jié)果表明：

(1)對于交替鋪層角度的玻璃鋼板，±45°鋪層角在0 Hz～1 000 Hz頻段內(nèi)具有更好的振動性能。

(2)增加激勵(lì)力的個(gè)數(shù)或者將等大載荷分布在盡量大的面積上，可以明顯降低玻璃鋼板的振動水平。

(3)增強(qiáng)玻璃鋼板的邊界約束條件能夠有效降低其振動水平。