基于決策樹的無車承運人平臺貨運任務定價模型

汪瓊枝，馬永傳

(皖西學院 金融與數學學院，安徽 六安 237012)

無車承運人是由美國track broker(貨車經紀人)這一詞匯演變而來[1]，是無船承運人在陸地的延伸，指的是不擁有車輛而從事貨物運輸的個人或單位。其一般不從事具體的運輸業務，只從事運輸組織、貨物分撥、運輸方式和運輸線路的選擇等工作[1]，已經有成熟的運行模式，具有多項優勢[2]。無車承運人平臺有三個參與角色：平臺、貨主、承運人。其利用互聯網平臺連接貨主和承運人，通過有效對接貨主與承運商的需求并促使其交易，極大改善了物流業資源閑置率高的狀況[3]。在其運行模式中，首先貨主在平臺發布貨運任務；接著平臺根據任務條件，給出貨運任務指導價格；最后承運人瀏覽任務，根據任務線路和價格自主選擇承運任務。如果平臺指導價格科學合理，能夠促進貨運任務快速成交，增加貨運任務交易的成功率，貨主、承運人、平臺三方均能獲益，從而提高平臺運行的整體效率。因此，如何對無車承運人平臺貨運任務科學定價，具有很強的研究價值和現實意義。

隨著我國無車承運人平臺的興起，國內也出現了一些相關研究。尤美虹、駱溫平、陶君成通過實地訪談和網絡調查[3]，調查分析了平臺監管問題。董娜綜合分析了平臺的內涵、優勢，提出了未來發展的建議[1]。金忠旭和郭躍顯利用物聯網等新技術，提出了基于互聯網+平臺的物流模式[2]。馮淑貞分析了發展現狀和相關的政策與制度問題[4]。張樹山課題組研究了平臺績效動態演化的趨勢，構建了績效演化的系統動力學模型[5]。基于普通公路貨運定價已經有了一些相關研究。顧敬巖和吳群琪[6]研究了我國公路貨運價格的演化趨勢，并提出了一些政策建議。王燕凌通過數據統計，分析了我國公路貨運市場的供求[7]。陳艷靜分析了公路貨運價格的影響因素，并給出了一些的完善運價形成機制的對策和建議[8]。馮芬玲和李杰潞分析了公路和鐵路的貨運價格和服務競爭，并建立了鐵路貨運和公路貨運的Hoteling模型[9]。但是，無車承運人平臺貨運任務定價模型的相關研究還很少。王聰珊等人給出了一個多元線性回歸模型，預測了平臺貨運定價[10]。聶福海和李電生基于信息不對稱理論，從博弈的角度研究了平臺的定價策略[11]。

決策樹是一種非線性監督機器學習，常用于分類和回歸[12]。其原理是通過從訓練集數據學習簡單推測規則，來預測目標變量的值。決策樹具有諸多優點：易于理解和應用、需要較少的數據預處理、預測算法為對數復雜度，訓練速度快、出色的數據分析效率、直觀易懂的結果展示[12]。決策樹有多個算法，其中CART(Classification and Regression Trees)決策樹算法由L. Breiman, J. Friedman, R. Olshen, and C. Stone提出[13]，是一種廣泛應用于分類和回歸的決策樹算法[14]。CART決策樹的回歸預測效果很好，已廣泛應用于多個領域，并取得了良好的效果。李曉寧等人利用CART決策樹預測平原河網區不透水面覆蓋度[15]。董紅召利用CART決策樹預測城市交通道路氮氧化物濃度[14]。韓家琪等人利用CART決策樹預測土壤水分[16]。許安定等人利用CART決策樹預測烤煙評吸質量[17]。探索使用CART決策樹來建立無車承運人平臺貨運任務定價模型，預測無車承運人平臺貨運任務價格具有良好的理論基礎和實際應用意義。

Pandas 是 Python 的核心數據分析支持庫，主要用戶數據整理與清洗、數據分析與建模、數據可視化與制表，具有高效、易用等特點，是目前流行的開源數據處理庫。

本文首先利用pandas庫分析了平臺貨運任務價格的主要影響因素，接著提出了一種基于CART決策樹的定價模型，預測平臺新任務價格，最后利用某無車承運人平臺的實際運行歷史交易數據，驗證模型的有效性，并與多元線性回歸算法進行對比，驗證了模型的優越性。

1 無車承運人平臺貨運任務價格的影響因素分析

要想準確的預測無車承運人平臺貨運任務的價格，首先需要找出影響平臺貨運任務價格的主要因素。

1.1 無車承運人平臺貨運任務價格的影響因素調研

通過調研現有的文獻并結合某無車承運人平臺的實際運行數據[6-9]，我們找出了可能對平臺貨運任務價格有影響的因素如下：

1)線路里程，線路里程是任務價格的直接影響因素，路程越長，成本越高，相應價格很可能越高。

2)業務類型(速運或重貨)，一般來說，重貨的成本要大于速運，相應價格可能越高。

3)是否區域發運，一般來說，區域發運的成本更低，相應價格可能越低。

4)計劃還是臨時，從博弈的角度考慮，臨時任務的價格可能更高。

5)車輛長度，車輛更長的貨車載重更多，相應價格可能越高。

6)車輛噸位，車輛噸位更大的貨車載重更多，相應價格可能越高。

7)運輸等級，即線路等級，路況不同，收費站不同等等，也會影響大價格。

8)緊急程度，從博弈的角度考慮，越緊急的任務價格可能更高。

對平臺以上因素的運行數據，我們首先需要進行量化處理。其中線路里程、車輛長度、車輛噸位數據、運輸等級可以直接使用。業務類型，是否區域發運，計劃還是臨時為二元數據，我們均將其轉化為數值0、1度量。緊急程度的原始數據為常規、緊急、特急，可將其轉化為數值0、1、2來度量。

接著，我們需要分析以上因素及實際運價之間的相關性。利用pandas庫，我們得出各影響因素及實際運價的相關系數如表1所示：

表1 影響因素及實際運價的相關系數

由表1可以得出：

1)車輛長度和車輛噸位相關性很高(0.99)。直觀上，我們也認為貨車越長，其載重量也越大。因此，這兩個因素，我們去除和價格相關性更低的車輛長度因素，保留車輛噸位因素。

2)車輛噸位和里程數相關性很高(0.816)。我們分析認為，這兩者缺少因果關系，因此兩個因素均保留。

1.2 基于灰色關聯度分析的貨運任務價格的影響因素分析

灰色關聯度分析法(Grey Relation Analysis, GRA)基于灰色理論分析系統因素間的相異程度[18]，通常用關聯系數來表示因素間關聯程度的大小[19]。方法具有對數據要求低、計算簡單等優點。因此，我們利用灰色關聯度分析來找出影響平臺貨運任務價格的主要因素。其具體過程如下：

1)確定自變量和因變量：我們用排除車輛長度后剩余的七個影響因素作為自變量，平臺貨運任務價格作為因變量。

2)歸一化處理：由于各數據量綱不同，我們采用最大最小化方法進行數據歸一化處理。

3)計算灰色關聯度：

設Xi=(xi(1),xi(2),…,xi(n)),i=1,2,…,m為平臺貨運任務價格的影響因素。Y=(y(1),y(2),…,y(n)) 為對應的平臺貨運任務成交價格。

γ(Y,Xi)為Y與Xi的灰色關聯度，則

(1)

其中

(2)

式(2)中ξ∈(0,1)為分辨系數。

其中灰色關聯度的計算步驟可細化如下：

Step 1：根據(3)式對平臺貨運任務價格的影響因素序列進行初始化：

(3)

Step 2：根據(4)，(5)式，計算平臺貨運任務價格的影響因素序列的差：

其中，

(5)

Step 3：根據(6)，(7)式求Δi(k)中的最大值M與最小值m：

Step 4：根據(8)式計算關聯系數：

(8)

Step 5：根據(9)式計算灰色關聯度：

(9)

根據灰色關聯度算法，計算得出七個影響因素的灰色關聯度，如表2所示。

表2 貨運任務價格的灰色關聯度

根據表2的結果，線路里程、區域發運、緊急程度、計劃或臨時對任務價格的影響程度很高，這也符合實際情況。

1)線路里程直接影響到運送的成本，里程數的增加增大了運送的成本，從而增加了最終運價。表1也表明了，里程數和實際運價有很強的正相關性。

2)緊急程度的增加，臨時的運輸任務，都會減少了愿意接單的承運人數量，從而增加了最終運價。表1也表明了，這兩個因素與實際運價的正相關性。

3)區域發運，可以降低運輸成本，從而降低了最終運價。表1也表明了與實際運價的負相關性。

4)業務類型分為速運(1)和重貨(0)，其中速運的成本要小于重貨，從而減少了最終運價。表1也表明了這種負相關性。

5)運輸等級與最終運價的關聯度不高，此因素可以去除。

最終得出平臺貨運任務價格的六個主要影響因素如下：線路里程、是否區域發運、緊急程度、計劃或臨時、車輛噸位、業務類型。

2 基于CART決策樹的無車承運人平臺貨運任務定價模型

我們采用CART決策樹，構建無車承運人平臺貨運任務定價模型，具體流程如下：

1)特征選取

選取上一章總結的六個運價主要影響因素為特征向量。

2)CART決策樹的生成

從根節點開始，從把所有訓練集數據放到根節點開始，通過選擇最佳特征，遞歸的將訓練集數據劃分到左右子集，即決策樹的左右分枝。

其劃分的過程如下：

Step 1：假設訓練集數據的容量是n，輸入變量為x，輸出變量為y。當選擇第j個特征向量x(j)及其取值v作為劃分特征和劃分點時，其兩個子集(子樹)定義如下：

式中，Rl(j,v)表示使用第j個特征變量及其取值v，劃分出的左子樹。Rr(j,v)表示使用第j個特征變量及其取值v，劃分出的右子樹。

Step 2：按(12)，(13)，(14)式求得最優劃分的特征變量j及劃分點v：

式中，yi表示輸入變量xi對應的輸出變量，xi∈Rl(j,v)表示使用第j個特征向量的取值v進行劃分，屬于左子樹的輸入變量。通過遍歷所有輸入變量，找到最佳劃分變量j和最佳劃分點v并構成一對(j,v)，然后依次將集合劃分至兩個子集。

Step 3：遞歸的進行上述劃分過程，直到滿足停止條件。

按照上述過程，我們實行了無車承運人平臺貨運任務定價模型，下一步我們將使用某平臺實際數據來訓練模型，測試效果。

3 數據和模型驗證

3.1 實驗數據

我們使用了某無車承運人平臺歷史運行數據，共16016條貨運任務來進行實驗。這些數據包括了任務id、線路里程、業務類型、是否區域發運、計劃或臨時、線路編碼、線路指導價、線路成交價、交易時間、車輛長度、車輛噸位、運輸等級、緊急程度等數據。根據第二章的研究，我們選取其中主要的六個影響因素的數據，將數據按8∶2的比例，采用隨機分配為訓練集和測試集。

3.2 評價標準

為了檢驗定價模型的效果。我們使用常用的誤差指標：均方誤差根(RMSE)和R-平方(R2)，并和傳統的多元線性回歸算法進行對比。

均方根誤差，是通過觀測值與真值偏差的平方與觀測次數n的比值的平方根來度量模型誤差，我們根據(15)式來進行計算。

(15)

我們根據(16)式計算R-平方，用其來判斷模型的擬合程度，R-平方值越接近1說明擬合程度越好。

(16)

3.3 實驗結果

我們的基于CARTR決策樹的無車承運人平臺線路定價模型，對數據集進行了5次隨機劃分，分別進行了訓練和測試，實驗結果如表3所示。

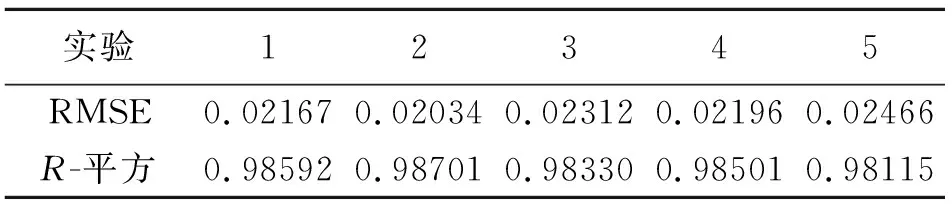
表3 基于CARTR決策樹的無車承運人平臺線路定價模型實驗結果

作為對比，我們使用多元線性回歸算法，以同樣的訓練集和測試集劃分，也分別進行了訓練和測試，實驗結果如表4所示。

表4 多元線性回歸實驗結果

從表3和表4可以看出，相對于多元線性回歸算法，我們模型的RMSE值均較小，且R-平方值均較大。結果驗證了模型的有效性和優越性。

4 結論與展望

本文針對無車承運人平臺的貨運任務定價問題，分析了平臺貨運任務價格的主要影響因素，提出了一種基于CART決策樹的定價模型，主要工作如下：

1)分析得出了平臺貨運任務運價的主要影響因素。

2)完成了整個定價模型的構建。

3)通過真實數據實驗驗證了模型的有效性，對比實驗結果表明了該模型優于多元線性回歸算法。

本文基于CART決策樹的無車承運人平臺的貨運任務運價模型的提出，豐富了運價模型相關的理論研究。同時，貨運任務運價模型能夠幫助平臺更為準確地給出任務的指導定價，促進了平臺任務的快速成交，提高了平臺的整體效率，提高了貨主、承運人用戶的使用體驗，具有良好的現實意義。

進一步的研究包括，尋找更好的定價因素，以及更優的擬合算法，以其獲得更好的定價預測。另外，當平臺任務過多后，平臺會面臨信息過載問題，此時準確的貨運任務定價并不能完全解決承運人快速尋找合適任務的問題，未來的研究可以考慮通過個性化任務推薦來解決平臺信息過載問題。