改進的直覺模糊加權Heronian幾何平均算子及其在徽酒評價中的應用
畢太苗,施明華
(皖西學院 金融與數學學院, 安徽 六安 237012)
集結算子作為信息融合的一種重要工具,是信息科學的重要組成部分。目前已被廣泛地應用于人工智能、優化研究、模式識別、圖像處理、決策科學等多個研究領域[1]。隨著時代的發展,人們所處理的信息往往帶有一定的模糊性和不確定性。為此,近年來學者們提出大量的模糊信息集結算子。例如:有序加權平均算子用于集結模糊語言信息[2]、直覺模糊信息[3]、猶豫模糊信息[4];有序加權幾何平均算子用于集結不確定語言信息[5]、三角直覺模糊信息[6]、區間猶豫模糊信息[7];優先級加權平均算子用于集結區間直覺模糊信息[8]、中智模糊信息[9]、區間猶豫模糊語言信息[10]。
上述集結算子假定信息集結過程中變量間是相互獨立的,而這一假設在實際操作中較難滿足。目前文獻大多使用Bonferroni平均算子和Heronian平均算子,對關聯程度較高的信息進行融合。文獻[11]將Bonferroni平均算子用于猶豫模糊語言信息的集結,并用于解決智慧醫療衛生系統中的多屬性決策問題;文獻[12]將Bonferroni平均算子用于生產庫存模型中的直覺模糊信息集結;文獻[13]進一步提出直覺模糊Bonferroni幾何平均算子,并用于求解金融投資中的多屬性決策問題。Heronian平均算子和Bonferroni平均算子一樣能捕獲變量之間的關聯性,但其計算量卻要明顯少于Bonferroni平均算子,近年來受到廣泛的關注。文獻[14]結合幾何平均算子和Heronian平均算子,提出了直覺模糊Heronian幾何平均算子和直覺模糊加權Heronian幾何平均算子;文獻[15]對猶豫模糊語言加權Heronian幾何平均算子進行定義,并給出一種多屬性決策問題的求解方法;文獻[16]給出了區間直覺模糊加權Heronian幾何平均算子,并用于電子政務績效評價的多屬性決策問題;文獻[17]將Heronian幾何平均算子引入語言環境下,定義了不確定語言加權Heronian幾何平均算子。但這些加權Heronian幾何平均算子在權重相相等時無法退化為Heronian平均算子,并且不滿足冪等性。
近年來隨著我國人民生活水平的提高,白酒行業得到快速發展。行業龍頭川酒、貴酒穩居領導地位,而處于第二梯隊的徽酒、鄂酒、蘇酒成為白酒行業的生力軍,市場占有率不斷擴大,品牌辨識度逐漸提高。以古井、口子窖、高爐家酒、迎駕貢酒、皖徽酒等“五朵金花”為代表的主流徽酒品牌,在中部地區有一定的市場影響力,近些年,依托其有效的營銷模式和清晰的市場定位,讓徽酒在市場中取得了不錯的突破,徽酒開始由曾經的地域性品牌向全國性品牌強勢邁進。口子窖首啟的“盤中盤”營銷策略,將重點放在核心消費者終端,取得了空前成功,有效開發和帶動了市場消費,品牌市場份額也得到大幅度提高。其后,該模式被其他徽酒企業效仿,也取得了不錯的業績。創新的營銷模式和有效的品牌策略,使徽酒在全國白酒市場逐漸站穩腳跟。但隨著越來越多白酒企業對這種營銷方式的效仿和跟進,市場競爭也在不斷加劇,導致各品牌搶奪市場酒店、餐飲等終端消費者的成本不斷攀升,而效果卻在減弱,導致企業利潤大幅度降低。徽酒這種同質化的營銷策略很難使其在未來發展中取得有效突破。從長遠來看,企業將營銷方向從過度關注產品、渠道促銷等方面轉向品牌運營,才能形成自己的核心競爭力,向良性發展之路邁進。另一方面,隨著消費升級趨勢的加快,人們的消費理念也在改變,他們開始追求健康飲酒、理性飲酒以及酒企背后的品牌文化。對于白酒企業來說,緊跟時代發展,打造鮮明的品牌,提供個性化、功能性產品才是大勢所趨。因此,對于徽酒進行評價,可以找出對徽酒品牌的影響因素,讓酒企更加清楚地了解自身的品牌現狀,從而進行改進提升,對其未來的品牌發展戰略有著至關重要的意義。
綜上所述,本文同時考慮到直覺模糊集理論能更好地處理復雜系統中的模糊性和不確定性,對加權Heronian幾何平均算子進行重新設計,提出一種改進的直覺模糊加權Heronian幾何平均算子,并證明新算子具有退化性、冪等性、單調性、有界性等良好性質,最后,將其用于解決白酒評價的多屬性決策問題。
1 預備知識
1.1 直覺模糊集
定義1[3]設X是一給定論域,則X上的一個直覺模糊集A為
其中μA(x):X→[0,1]和υA(x):X→[0,1]分別代表A的隸屬函數和非隸屬函數,并且?x∈X有0≤μA(x)+υA(x)≤1.
為便于計算和討論,將直覺模糊集中的元素用有序區間對α=(μα,υα)表示,并稱為直覺模糊數。設α=(μα,υα)和β=(μβ,υβ)是2個直覺模糊數,規定:
1)α⊕β=(μα+μβ-μαμβ,υαυβ);
2)α?β=(μαμβ,υα+υβ-υαυβ);
為對直覺模糊數α=(μα,υα)和β=(μβ,υβ)進行排序,Chen等人提出得分函數[18](P13-18),[19]:sα=μα-υα;Hong等人引入精確度:hα=μα+υα;Xu等人將二者相結合,給出如下的排序方法[20]:
· 若sα>sβ,則α>β;
· 若sα=sβ,則
(ⅰ) 當hα=hβ時,有α=β;
(ⅱ) 當hα>hβ時,有α>β.
1.2 Heronian幾何平均算子
定義2[14]設p≥0,q≥0,且p與q不同時為0,αi=(μαi,υαi) (i=1,2,…,n)為一組直覺模糊數,若
則稱IFGHMp,q為直覺模糊Heronian幾何平均(GHM)算子。
但上述Heronian幾何平均算子僅考慮了變量間的關聯性,忽略了權重信息。為此,Yu等人進一步給出如下定義[14]。
定義3[14]設p≥0,q≥0,且p與q不同時為0,αi=(μαi,υαi) (i=1,2,…,n)為一組直覺模糊數。若
則稱IFWGHMp,q為直覺模糊加權Heronian幾何平均(IFWGHM)算子。
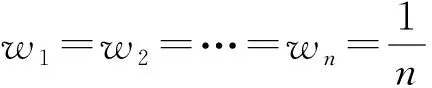
2 改進的直覺模糊WGHM算子

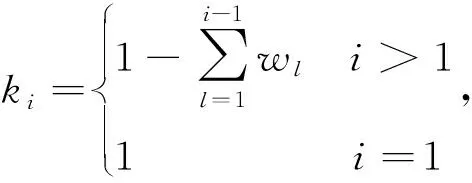
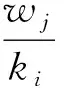


進而有
(1)
故有
下證,由IIFWGHM算子的集結值是直覺模糊數。
由0≤μαi≤1,0≤υαi≤1,易知
和
又
綜上定理得證。
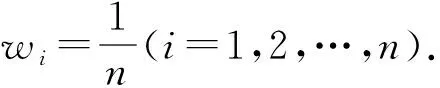

因此
定理3(1) (冪等性)αi(i=1,2,…,n)為一組直覺模糊數,若αi=α(i=1,2,…,n),則有
(2) (交換性)αi(i=1,2,…,n)為一組直覺模糊數,若α′1,α′2,…,α′n為α1,α2,…,αn任一置換,則有
(3) (單調性)αi=(μαi,υαi),βi=(μβi,υβi)(i=1,2,…,n)為兩組直覺模糊數,若對任意的i=1,2,…,n,都有μαi≤μβi,υαi≥υβi,則

證明:(1)
(2)
(3) 因為μαi≤μβi,υαi≥υβi(i=1,2,…,n),故有
從而
同理可得
所以
不妨設IIFWGHMp,q(α1,α2,…,αn)和IIFWGHMp,q(β1,β2,…,βn)的得分函數和精度分別為sα、sβ以及hα、hβ,則由上式得sβ≥sα.
1) 若sβ>sα,則直接可得
IIFWGHMp,q(α1,α2,…,αn)
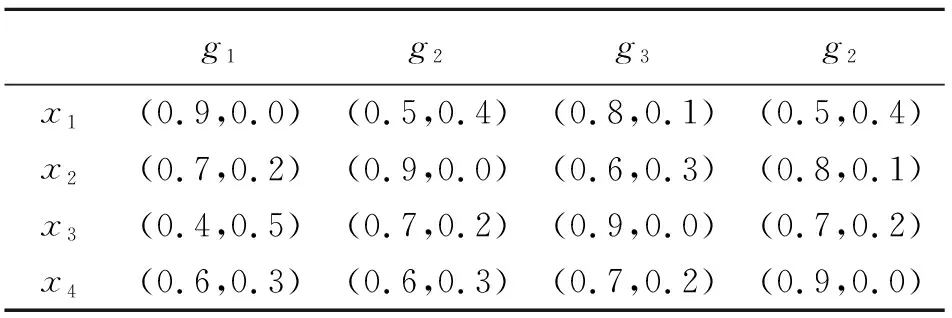
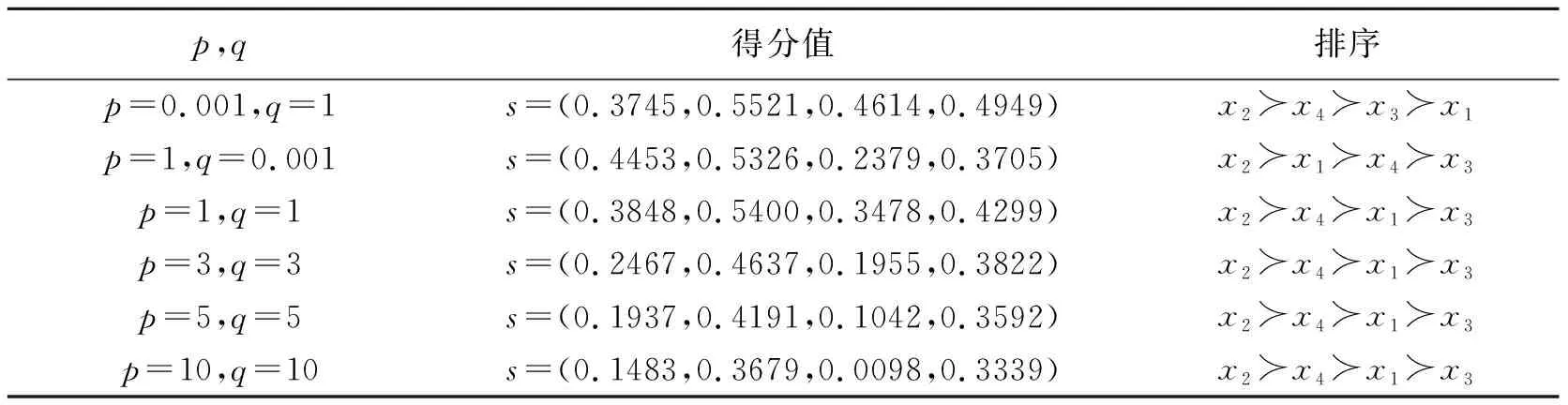
2) 若sα=sβ,結合μαi≤μβi,υαi≥υβi(i=1,2,…,n),可得 和 從而有hα=hβ,因此 綜上,(3)成立。 (4) 由(1)和(3)可得 和 即 綜上,定理3得證。 下面我們給出IIFWGHM算子的一些特殊形式。 情形1若p=0, 則有 情形2若q=0, 則有 情形3若p=1,q=1,則有 注:1) 由情形1和2可知參數p,q不具備交換性,即 2) 當q=0時IIFWGHM算子無法捕獲變量的權重信息。 在前文定義的IIFWGHM算子基礎上,給出上述決策問題的求解步驟,具體如下: 步驟3:依次計算上述綜合評價值的得分值(如需要,則進一步計算精度值),利用方案綜合評價值的得分對決策方案進行排序,并選擇最優方案。 假定某公司打算選擇某徽酒品牌進行投資,經過前期的市場調研,4種徽酒品牌(x1,x2,x3,x4)進入備選。智囊團的成員決定從以下4個因素(對應的權重為w=(0.2,0.3,0.3,0.2)T),對各4種徽酒品牌的進行評估: g1-支持力,指的是品牌受關注度和社會的認可度,具有強大支持力的品牌在市場中的傳播力度更加強勁,而且能夠獲得較強傳播投資和營銷支持; g2-市場力,指的是品牌在市場中的占有率。一個具有較大市場占有率的品牌,在市場中的認知度會明顯優于其他品牌,競爭優勢也增強; g3-行銷范圍,指品牌的銷售區域,擁有較強的跨區域、跨文化傳播的能力。若該品牌行銷范圍廣,則在市場更具有認知度和聲望; g4-趨勢力,指的是品牌是否能與企業未來發展相契合,具有良好趨勢力的品牌能夠順應市場的發展,抓住消費者的需求和變化,并與之保持同步。 最終,專家組達成一致評價意見,并給出如下的直覺模糊信息評價矩陣。 表1 直覺模糊信息評價矩陣 為選擇最佳建設方案,下面利用本文的決策方法進行求解,具體步驟如下: 步驟1:題中涉及的屬性均為效益型指標,因此無須規范化,可直接進行優選決策; 步驟2:利用IIFWGHM集結算子對上述評價矩陣第i行進行集結,得到方案的綜合評價值,具體如表2。 表2 IIFWGHM算子集結結果 步驟3:計算各徽酒品牌綜合評價的得分值,并據此進行排序(如表3所示),為公司選擇最佳投資品牌。 從表3可見p,q取值不同時,盡管最佳選擇是x2,但整體排序卻不一致。由此可知,IIFWGHM算子決策方法依賴于參數取值,考慮到計算復雜性等因素,一般情況下建議決策時取p=q=1。從表2以及表3我們還可以見到一個有趣的現象,當p,q取值相等時,參數取值越大,評價值和得分值越低。事實上,可以證明p=q時,IIFWGHM算子是關于參數遞減的,對于樂觀者可以選擇取值較低的參數,而悲觀者則相反。但過大的參數也會導致模型識別能力降低,例如本題中p=q=30時,x2~x4~x1?x3.因此決策過程中要合理的選擇參數進行決策。 表3 決策結果 下面我們將本文方法同已有的直覺模糊多屬性決策方法進行對比,由于這些方法的主要區別在于使用不同的集結算子,因此我們有重點的選取直覺模糊加權Heronian平均(IFWHM)算子[21],直覺模糊加權幾何Heronian平均(IFWGHM)算子[14],以及直覺模糊加權Bonferroni平均(IFWBM)算子[22],同本文的改進的直覺模糊加權幾何Heronian平均(IIFWGHM)算子進行對比,具體結果如表5所示。 表4 方法比對結果 在經濟社會快速發展的今天,人們所面臨的信息往往具有一定的不確定性和模糊性,直覺模糊數是處理此類信息的一種有效技術。本文對于現有的加權幾何Heronian平均算子進行設計,給出了一種具有退化性以及冪等性等優良性質的直覺模糊加權幾何Heronian平均算子。此外,基于新設計的算子,提出一種多屬性決策方法,徽酒品牌評價案例表明方法的可行性和有效性。3 直覺模糊多屬性決策方法

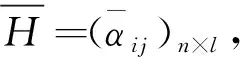
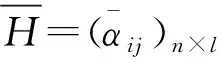
4 實例分析

5 比較分析

6 結論

