宏觀角度對福建省就業影響因素的分析與探討
一、前言
眾所周知,充分就業是每一個國家都必須面對的熱點問題,同時也是每個國家重要的經濟發展目標。世界上各個國家的就業狀況并不容樂觀,時有波瀾。而我國就業形勢雖然也面臨著重大的挑戰,但是在經濟高速發展之下,新增就業崗位數得到快速增長,僅針對福建一省所收集到的20年數據來看,就業人數增長迅速,有著顯著的上升趨勢。福建的地理位置比較特殊,它位于我國的東南沿海,是長江三角與珠江三角的連接點,并且與臺灣相隔不遠,因此,福建省在我國經濟發展中也有著特殊的戰略地位,對福建省就業影響因素的研究就顯得尤為重要。
針對我國的現狀、福建省的現狀,建立一套對于就業人數的科學的預測體系是把握住控制就業的主動性的前提。因此,本文想收集大量的歷史數據,通過利用統計學的知識與R語言科學地分析福建省就業的影響因素,建立回歸模型,進而對就業人數進行預測,并將預測的結果與現實情況進行對比,判斷模型是否有效。
查閱相關的資料,可知影響就業人數的主要因素有:地區生產總值、每萬常住人口擁有的在校大學生數、人口自然增長率、稅收、教育支出。本文將這些因素作為變量、就業人數作為因變量,對二十余年的具體數據建立回歸方程,進行多重共線性、異方差、自相關的檢驗與消除,用最后確定的模型進行對就業人數的預測,對比分析結果,解釋其中存在的互動關系。最后初步進行總結,提出相應的政策建議,以促進福建的就業人數的增長,優化就業結構,營造良好的就業環境,以實現充分就業的經濟發展目標。
二、模型與求解
(一)數據
使用數據為1997-2007年福建省就業相關數據,共21條。包括5個自變量變量(地區生產總值、每萬常住人口擁有在校大學生數、人口增長率、稅收、教育支出)和一個因變量(就業人數)。數據來自《中國統計年鑒》《福建統計年鑒》(1997年至2017年)。
利用R語言將數據導入并得到散點圖。由散點圖可見x1地區生產總值、x2每萬常住人口擁有在校大學生數、x3人口自然增長率、x4稅收、x5教育支出與y就業人數基本呈線性關系,所以初步可以建立方程。
(二)線性回歸
初步建立回歸模型可知x1、x2與x4對y起正影響,x3與x5對y起負影響,這與定性分析結果顯然不一致,從數據可直接看出這5個變量對y都起正影響,原因可能是自變量數目太多,變量之間存在著相關關系。
給定顯著性水平為0.05,x3相應的p值為0.103234,沒有通過回歸系數的顯著性檢驗,說明x3對因變量的影響不顯著。決定系數為0.9949,從相對水平上看,回歸方程能解釋因變量y的99.49%的方差波動。回歸標準差為35.95。回歸模型的F值為585,p值<2.2e-16,由此可知回歸方程整體上高度顯著,這與相關系數的檢驗結果是相一致的。
(三)多重共線性診斷與消除
多元線性回歸模型的一個基本假設即設計矩陣X的秩rank(X)=p+1。即要求各解釋變量之間線性無關。而這一假設在實際問題中卻是常常難以滿足的,比如在該研究問題中,涉及了5個自變量,自變量的數目比較多,并且很難從其中找到一組自變量,它們之間是完全不相關的關系。在實際的問題中,如果一個經濟社會現象受到多個重要的因素影響時,這些解釋變量之間往往有一定的相關性。當解釋變量的相關性比較弱時,我們可以認為近似滿足多元線性回歸模型的基本假設;當一組變量之間的相關性比較強時,就認為違背了基本假設。
x1,x2,x3,x4,x5之間的相關系數很高,且在第三步線性回歸中,x3與x5的回歸系數正負號與定性分析結果相違背,這初步說明了該模型有多重共線性。這與基本預測是相一致的,當所研究的經濟社會問題是關于時間序列的資料時,由于這些變量隨時間往往有著相一致的變化趨勢且關聯密切,多重共線性的問題很難避免。因此進行逐步回歸,并且按照AIC準則刪去多余變量,對剩下變量做回歸。
從輸出顯著性結果可看出,當保留x1,x2時,各參數t檢驗通過,說明模型擬合較好。決定系數為0.9913,從相對水平上看,該模型能解釋因變量y的99.13%的方差波動。回歸標準差為42.92。從方差分析表中可以看到,回歸模型的F值為1023,p值<2.2e-16,由此可知回歸方程整體上高度顯著。
因此,最終方程為y=1422+0.03387x1+1.656x2。
(四)異方差檢驗及自相關檢驗
現實中的問題是充滿復雜性的,對于此類問題進行回歸分析時,往往其中的某些因素隨著解釋變量觀測值的變化,而對被解釋變量產生復雜的影響,導致隨機誤差項產生不同的方差。當一個回歸問題存在異方差時,常常會破壞模型的有效性,因此本模型中需要對異方差進行檢驗。
異方差的檢驗結果可看出,P=0.05638>0.05,說明模型不存在異方差。
在時間序列中,往往會出現正的序列相關。而建立線性回歸方程的一個基本假設就是其中的隨機誤差項不存在序列相關。因此,診斷隨機擾動項是否存在自相關性,對于問題的研究和模型的建立是一個重要的方面。
對模型進行自相關的檢驗,可得P=0.1812>0.05,因此該模型不存在自相關。
三、模型檢驗
(一)殘差圖與回歸散點圖
一個模型通過了t檢驗或者F檢驗并不能夠確保這個模型是有效的或者這個模型對數據擬合得很好,只是說明解釋變量與被解釋變量之間有比較顯著的線性關系。還時可能存在其他的一些問題導致數據并不可靠。比如異常值與周期性干擾。殘差值是實際數據與通過回歸方程得到的回歸結果之間的差值。只有通過檢驗殘差項相關的檢驗,才能夠保證回歸模型的正確性可靠性。因此在以下的步驟中,通過使用殘差圖,來判斷模型的效果與質量,檢驗基本假定是否滿足。
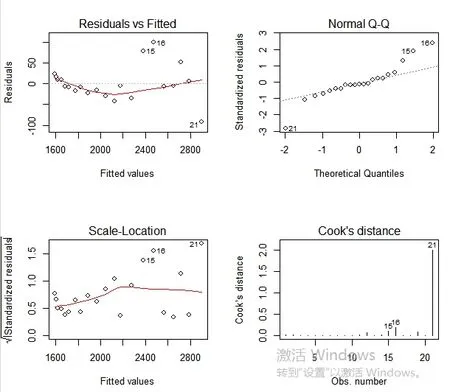
圖1 殘差圖與回歸圖
圖1可以看出,第15、16、21樣本點顯然出現了不同程度的偏離,因此可以將這三個點看做異常點。在接下來的步驟中進一步確定這三個點是否存在問題。
(二)正態性檢驗
如果殘差是正態分布,那它就是具備著隨機性的,進一步可以看做比較好的擬合了隨機誤差。
對殘差進行正態性檢驗可得,P=0.1046>0.05,說明模型的殘差是正態性的,滿足了線性回歸模型的假設。
四、模型預測
利用R語言對建立的模型求得預測結果與預測區間。將預測輸出結果與實際數據做對比分析,發現實際的數據都落在預測區間內,因此表明此模型的擬合效果很好。
五、結論與對策建議
(一)結論
最終得到的結果模型為:y=1422+0.03387x1+1.656x2。
可以看出,在其他變量不變的情況下,地區生產總值每增加1億元,就業人數增加0.03387萬人;每萬常住人口擁有大學生數每增加1人,就業人數增加1.656萬人。
(二)政策建議
通過對福建省就業因素的研究可以看出,從宏觀經濟來講,地區生產總值會對就業人數的上升起到積極的影響。當社會開始出現經濟衰退、生產消費不振時,常常伴隨著失業人數增加、勞動力供給水平降低的情況。政府在就業問題中起著關鍵的作用,科學有效的財稅政策對于社會經濟發展起到重要的指導作用。政府需要扮演好自己的角色,掌控好宏觀經濟,才能保持經濟穩定增長與繁榮,促進社會發展,最大程度降低失業率,實現充分就業。從發展產業來看,短期內就業增長最有效的方式是把重點放在勞動密集型企業,以此增加人民就業;而從長期來看,技術與資本密集型企業是經濟發展的最大帶動力,以此才能在這個科技高速發展的時代保持長期穩定的經濟繁榮。在政策制定時應該二者兼顧,做好短期與長期的有機鏈接,將經濟增長與帶動就業更好的結合起來。
除了社會宏觀經濟方面的影響,每萬常住人口擁有的大學生數也是就業增長的一個重要因素,從中體現出來的是教育問題、人才培養問題。政府部門應該考慮加大對教育方面的財政投入,對教育結構進行科學的調整,引導社會各界的力量去促進教育的發展,切實提高教育質量。除此之外,政府也應該考慮到教育資源分配不協調的問題,現如今,寒門越來越難出貴子,教育資源應該往農村地區貧困地區有所傾斜,保證貧困家庭孩子也能接收到高質量的教育,這是促進貧困地區弱勢群體經濟內生增長的有效方式。

