天氣衍生品定價研究

鄒楚瑜

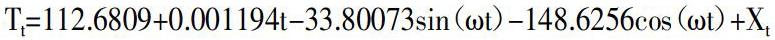
[提要] 天氣衍生品是交易資產為標準化的天氣指數的金融衍生工具。作為新型的天氣風險管理工具，其風險對沖的效果主要由定價模型的預測精度決定。因此，本文使用北京市近60年每日平均氣溫數據，基于ARIMA模型擬合北京市平均氣溫動態變化過程，并結合蒙特卡洛模擬法對氣溫期貨進行定價，考察ARIMA模型的預測精度。研究表明：ARIMA模型能夠較好地擬合氣溫動態變化過程，并且以此為基礎得到的氣溫期權價格能夠較好地擬合實際價格。

關鍵詞：天氣衍生品;ARIMA模型;蒙特卡羅模擬法

基金項目：河北省教育廳重點項目：“農業信貸結構、配置效率與河北省農業經濟增長”（編號：SD191051）

中圖分類號：F830.91 文獻標識碼：A

收錄日期：2020年7月20日

一、引言

隨著全球氣候變暖的不斷加劇，極端天氣發生的頻率陡增，災害破壞力不斷加大，各國基礎設施、民生和經濟發展正在面臨日益凸顯的威脅。而中國是世界上自然災害發生最為頻繁、災害種類最多，造成損失最為嚴重的國家之一，其中干旱、暴雨洪澇、寒潮、臺風等災害對經濟社會發展的威脅程度愈發升高，因此對于天氣風險的防范工作必須得到廣泛關注。相較于上述災難性天氣對經濟社會的毀滅性破壞，社會各界對于近年來出現的一般性天氣異常現象的重視程度嚴重不足，例如連續多日高溫、雨季提前到來、暖冬等，這些現象對于一國經濟的影響不像災難性天氣那樣來得迅速、猛烈，但其無異于“溫水煮青蛙”，最終可能對一個行業或者整個經濟社會產生難以估量的持久不可逆傷害。而我國目前對于上述風險的防控措施十分匱乏，進入21世紀后，天氣保險被廣泛地運用于災難性天氣的防控和賠償之中，但這種產品對于應對一般性的天氣異常現象幾乎沒有任何幫助。因此，致力于對沖上述一般性天氣風險的天氣衍生品逐漸得到政府機構和學術界的重視。

天氣衍生品是以氣溫、降雨量、風力等氣象數據計算的天氣指數作為交易對象，用以防范宏觀、中觀和微觀經濟主體所面臨的一般性天氣風險的新型金融衍生品。1997年發生的厄爾尼諾暖冬事件促使美國能源企業科赫與安然首次簽訂天氣互換合約，這是天氣衍生品迄今為止最早的場外交易記錄。1999年，天氣衍生品的場外交易規模迅速膨脹，倒逼芝加哥商品交易所（以下簡稱CME）設計并發現標準化的1月期氣溫指數期貨合約，由此天氣衍生品場內交易市場正式建立。隨后逐漸推廣至歐洲其他發達國家資本市場、日本以及發展中國家之中，交易量迅速攀高。

定價研究是天氣衍生品研究的熱點。用于天氣衍生品定價的模型眾多，目前學界關于定價模型達成了一個共識，那就是傳統金融衍生工具的無套利定價理論在天氣衍生品定價領域不適用，因為天氣衍生品的交易資產是不可交易的天氣指數，而不是可以實物交割的資產。此外，由于CME市場上流通的產品近90%都以溫度指數為交易資產，因此大多數學者的研究主要以溫度為標的物的天氣衍生品為主，通過各種數理模型來預測氣溫的動態變動過程并為相應的產品進行定價。天氣衍生品的定價模型大致可分為以下兩類，即ARMA模型等傳統時間序列模型和均值回復模型。傳統的時間序列模型的基本實證過程較為相似，大體上是在剔除氣溫時間序列當中的趨勢性因素和季節性因素的基礎上，使用ARMA模型等時間序列模型對殘差序列進行建模，然后再結合蒙特卡洛模擬法對相應產品定價。學界使用的均值回復模型基于氣溫的隨機變化在長期傾向于回歸均值水平的假設，通過不同的氣溫波動率，如日氣溫波動率和月氣溫波動率，結合Alaton（2000）提出的隨機微分方程（SDE）來構建模型，最后再依靠蒙特卡羅仿真模擬法對相應產品進行定價。

當前，國內外學界在天氣衍生品領域研究的重心不同，國外主要集中于天氣衍生品定價問題的探索和改良，而國內大多數學者當前還停留在基礎的名片式定性研究當中，研究進展相對落后。因此，本文著眼于天氣衍生品定價研究在國內的推廣，選擇北京市作為研究對象，基于ARIMA模型來擬合北京市的每日平均氣溫動態變化趨勢，并以此為基礎結合蒙特卡洛模擬法來對天氣期權開展定價研究。

二、數據與研究方法

（一）數據說明。本文選取北京市1960年1月1日至2018年12月31日的日平均氣溫數據（消除閏年影響后，共計21，535個數據）作為實驗組的數據樣本，2019年1月1日至2019年12月31日共計365個數據作為測試組的數據樣本。全部數據樣本均取自中國氣象局數據共享網。

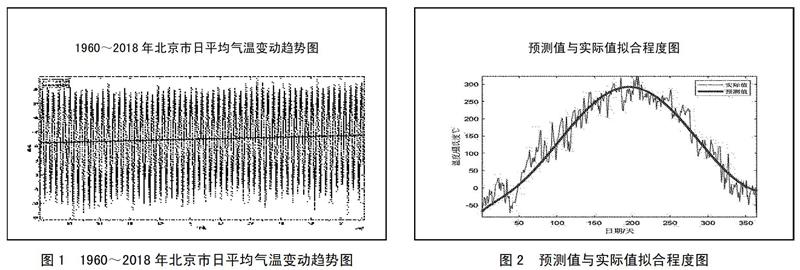
通過繪制氣溫變動趨勢圖來直觀地呈現氣溫在區間內的變動情況，如圖1所示。可以觀察到平均氣溫存在明顯的周期性變化和緩慢的線性遞增趨勢，這意味著北京市的平均氣溫在近60年不斷的四季更迭中呈現出略微變暖的趨勢。（圖1）

（二）模型的設定。首先，根據傳統的時間序列分析理論將模型的基本形式設定為：

其中，Tt為日平均氣溫序列，St為氣溫變動的線性以及季節性趨勢變量，而Xt為剔除線性和季節因素后的隨機變量（殘差）。

從圖1不難發現，北京市近年來氣溫的變動趨勢比較接近于正弦函數曲線，此外圖1還呈現出略微的線性遞增趨勢，因此t時刻的趨勢變量St可以表示為線性趨勢和周期性趨勢兩部分。具體形式如下：

其中，a+bt為平均氣溫序列的長期線性遞增趨勢，βsin（2πft+？漬）為氣溫序列的周期性變動。β為曲線的振幅，平均氣溫將在區間[-β，β]內波動;f為曲線的頻率，曲線在1/f個時間單位內重復變動趨勢，1/f被定義為最小變動周期，本文取f=1/365，此時的最小周期為365天（1年）。？漬為曲線的相位，表示平均氣溫在時間軸上的任意初始值。

上式可以通過三角函數變換進行進一步簡化，如下所示：

由于相位角為常數，可以進一步化簡得：

將公式（4）代入公式（1）中，得到平均氣溫序列Tt的最終表達式如下所示：

三、參數估計與結果分析

（一）ARIMA模型的參數估計。結合公式（5），通過Eviews10.0軟件對氣溫時間序列進行普通最小二乘估計，得到待估參數的估計輸出結果如表1所示。（表1）

由表1的輸出結果可知，在0.05顯著性水平下的各系數值顯著大于臨界值且擬合優度較高，說明模型擬合效果較好。將參數代入式（5），可得：

從表1還可以觀察到DW統計值僅為0.547，查表可知氣溫時間序列Tt可能存在一階序列相關，這可能是殘差Xt導致的，因此需要對Xt進行修正。將趨勢變量St從Tt中剔除后，即可得到殘差Xt。通過繪制殘差序列圖判斷出Xt可能不存在顯著的序列相關性。通過對殘差Xt進行單位根ADF檢驗，可以判斷出在多種信息準則下，一階差分的殘差Xt是一個平穩序列。通過繪制一階差分的Xt的自相關系數圖和偏自相關系數圖，可以判斷出該序列是平滑的非白噪聲序列，因此需要構建ARIMA模型對其進行擬合。根據AIC準則、Schwarz準則和參數的顯著性判斷，引入ARIMA（2，1，2）模型最為恰當，擬合的具體結果如表2所示。（表2）

從表2中可以看出，各項系數都是顯著的，且模型估計的DW統計量為2.002453，十分近似于2。因此，可以初步認為構建ARIMA（2，1，2）模型之后，殘差序列中原先存在的相關性問題得到適度的修正。因此，可以得到一階差分的殘差序列Xt和氣溫時間序列Tt的表達式如下：

（二）模型擬合的精確度檢驗。根據上式，運用Matlab對2019年北京市日平均氣溫進行預測，并與2019年實際的平均氣溫進行比較，得到圖2。觀察該圖能夠得出，通過ARIMA（2，1，2）修正后的模型能夠較為精準地擬合平均氣溫的動態變化過程。（圖2）

四、天氣衍生品定價

（一）天氣指數選取。天氣衍生品是以天氣指標轉換而來的指數作為交易資產，其中使用最普遍的天氣指數是累積供暖指數（HDDs），被定義為一定時期內的每日平均氣溫與基線溫度之間偏差的累計值。基線溫度是一個臨界溫度，當氣溫低于該值時，社會各界傾向于開展供暖活動，而當氣溫高于這一數值時，人們更愿意采取降溫措施。不同交易所對基線溫度的定義不同，現在最常用的是CME設立的華氏65度（18攝氏度）。HDDs指數的表達式如下：

其中，HDDi是每日的供暖指數，Ti為第i天的平均氣溫，Tref是基線氣溫。

（二）基于蒙特卡洛模擬的天氣衍生品定價。本文選擇基于累積供暖HDDs指數的歐式看漲期權進行定價研究。假設期權為歐式期權（即買方只有在行權日T當天行權的權利），標的指數為HDDs指數，K為合約執行價格，C為價值轉換因子（將沒有實際貨幣價值的HDDs指數轉化為具體的貨幣量），U為期權的上限值，r為合約期限內的無風險利率。于是在風險中性條件下，基于HDDs的歐式看漲期權在時刻t的價格如下所示：

其中，HDDs（0，t）是時刻t之前的HDDs數據，是已知量;而HDDs（t，T）是從時刻t到行權日T的HDDs，是需要通過蒙特卡洛模擬來進行仿真的。

結合公式（5）和公式（6），利用蒙特卡洛仿真模擬法進行預測，得到這一期限內基于不同基線溫度的累積供暖指數HDDs的期望值，將其和該期限內實際的HDDs指數進行對比得到表3。其中，相對誤差率代表真實值相對于預測值的偏離程度。（表3）

從表3中不難看出，在五種基線溫度下的相對誤差率均小于6%，預測精度較高;另外，隨著基線溫度的升高，相對誤差率遞減。

假設北京市2019年2月份的HDDs歐式看漲期權的執行價格K=200（參考現值有利法，設定為低于歷年同期水平的價格），合約名義價值C=20，上限值U=10000，無風險利率r=2.72%（取自2019年2月份的一月期SHIBOR利率）。因此，在風險中性條件下，基于不同基線溫度的期權價格匯總結果如表4所示。（表4）

從表4中的數據可以發現，在五種基線溫度下的相對誤差率均小于10%，預測精度較高;另外，隨著基線溫度的升高，相對誤差率遞減，且在基線溫度為20攝氏度時的相對誤差最小，僅為6.85%，這說明將基線溫度設定在20攝氏度左右可能更適合于當前我國市場的基本情況。

五、我國天氣衍生品開發及市場發展建議

目前，我國正面臨著日益增大的天氣風險管理需求與匱乏的天氣風險管理工具供給之間的矛盾，諸如天氣保險、政策補貼等傳統意義上的天氣風險管理工具的作用范圍和效果有限。而天氣衍生產品已經經過了西方資本市場長達二十余年的檢驗，是一種合格的天氣風險管理工具，應該在我國進行適度推廣，這不僅需要正確的意識基礎，還需要先進的技術支撐和良好的政策環境。

第一，培養正確的天氣衍生品風險管理意識。想要推廣天氣衍生品，當務之急就是讓社會各界開始認識、理解并且重視該產品，進而形成正確的天氣風險意識，最終培養出數量穩定的市場需求。

第二，進一步發展氣象技術、數據分析技術以及金融工程技術。天氣衍生品的精準定價要求氣象數據盡可能的全面和精準，首先就要求有關氣象部門觀測、歸納以及共享更為豐富且精準的氣象數據;其次需要發明更加先進的數據算法、信息系統等數據分析技術，以便更加高效、準確地處理龐雜的氣象數據。不僅如此，還應研究出更為先進的金融工程學理論和實踐方法，這樣才能將抽象的氣象數據轉化為社會經濟需要的金融產品。

第三，孕育良好的政策和投資環境。天氣衍生品在開發、推廣和交易中都需要經費支持和政策扶持來抵御較大的不確定性，這就要求政府提供一些切實有效的幫扶政策來分擔市場參與者的成本和風險，鼓勵更多的機構、企業和個人進入證券市場來轉移天氣風險，孕育足夠具有吸引力的政策環境。同時，市場監管部門應當進行嚴格的監管和規范，加強對市場準入、信用風險、信息披露以及行業自律的把控力度，必要時可以引入做市商制度來保證天氣衍生品發行初期的流動性和價格的合理性，為天氣市場的投資者培養出優異的投資環境。

主要參考文獻：

[1]劉國光.天氣預測與天氣衍生產品定價研究[J].預測，2006.25（6）.

[2]劉國光，茅寧.氣溫隨機模型與我國氣溫期權定價研究[J].數理統計與管理，2008.27（6）.

[3]李永，夏敏，吳丹.O-U模型在天氣衍生品定價中的合理性測度[J].統計與決策，2011.345（21）.

[4]郭建國，牛珊.基于ARMA模型的氣溫衍生品定價研究[J].商業經濟，2015.470（10）.

[5]曾小艷，陶建平.基于ARMA模型的氣溫衍生品定價研究：以武漢市為例.區域金融研究，2014.500（7）.

[6]Dischel，B.At last：A Model for Weather Risk [J].Energy and Power Risk Management，1998.11（3）.

[7]Dornier，F.，Queruel，M.Caution to wind[R].Energy Power Risk Management，Weather Risk Special Report，2000（1）.

[8]Alaton，P.，Djehiche，B.，Stillberger，D.On Modelling and Pricing Weather Derivatives[J].Applied Mathematical Finance，2002.9（1）.