基于Matlab 的標槍形心位置研究
陳 瑞,蘇小珂,肖人峰,田才艷,張 斌
(成都信息工程大學 通信工程學院,四川 成都610000)
1 引言
在標槍運動中,標槍投擲距離的大小分別受運動員能力、標槍的技術參數和比賽環境三方面因素的影響[1]。其中運動員能力包括出手速度、出手角、初始攻角、出手高度、出手時標槍的初始俯仰角速度等,標槍的參數有長度、質量、幾何形狀、重心的位置、形心的位置等,環境因素有空氣的密度與粘度、風力、風向等[2]。在本問題中,為了簡化討論作出了如下假設:運動員出手高度為2 m,標槍質量為800 g,不考慮標槍在飛行過程中的進動影響,空氣密度為1.184×10-3g/cm3,空氣粘度為1.84×10-5Pa·s[3]。
2 模型1 的建立與求解
根據題目所提供的標槍基礎數據,求出標槍沿標槍中軸線剖面面積、標槍表面積和標槍形心的位置。使用MATLAB、相關數學以及物理知識進行求解。步驟如下:根據標槍基礎信息,使用MATLAB 將標槍外輪廓畫出;將標槍進行分段擬合;使用一重積分求出標槍沿標槍中軸線剖面面積;使用旋轉曲面求積分求出標槍的表面積;通過多邊形形心公式求出形心位置。
2.1 標槍外輪廓圖的繪制
通過MATLAB 的繪圖功能將附件所給的標槍基礎數據繪制成標槍的外輪廓。
2.2 標槍分段擬合
將標槍分為6 段,如表1 所示。
各段擬合函數f(x)如下所示:
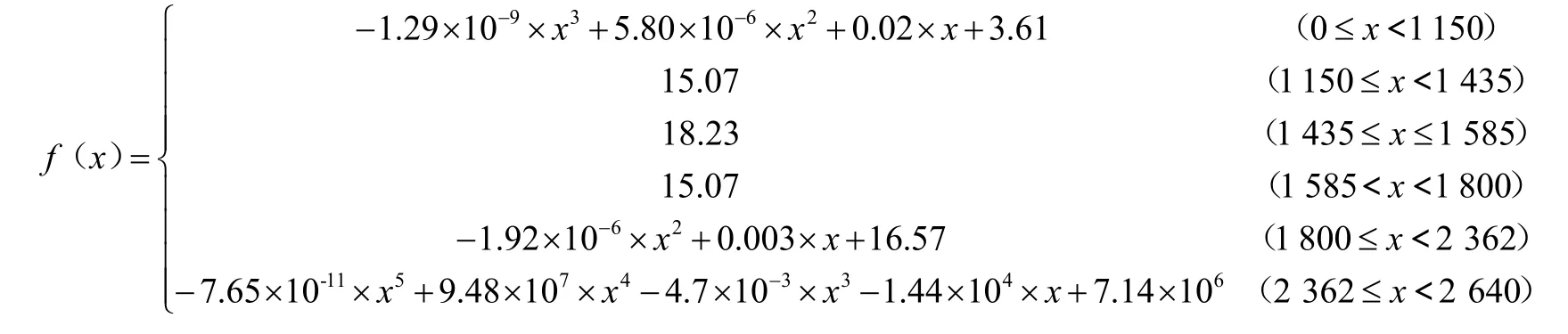

表1 標槍分段
2.3 求解沿標槍中軸線剖面面積
沿標槍中軸線剖面即為標槍外輪廓,所以通過計算一重積分的方法來計算外輪廓的面積,也就是沿標槍中軸線剖面面積。

使用MATLAB求解公式求得剖面面積為S1=0.064 6 m2。
2.4 求解標槍表面積
若想求出標槍表面積可以通過高數中求解旋轉面積分算法。

使用MATLAB求解公式所求標槍表面積S2=0.201 2 m2。
2.5 求解標槍形心的位置
使用多邊形的形心公式可以較為簡便地得出形心的位置剖面面積為:
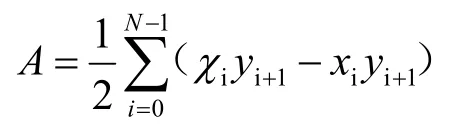
剖面的形心由下式給出:
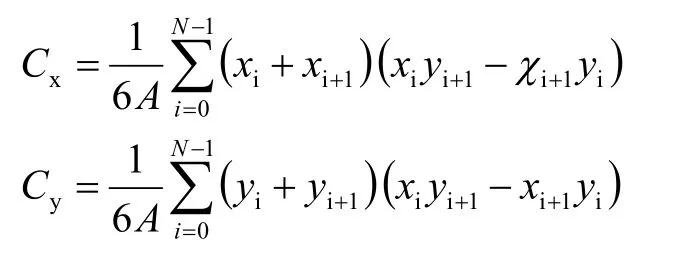
本文使用MATLAB 軟件將公式實現,最終得出標槍形心的位置。
3 模型2 的建立與求解
3.1 多元線性回歸方程的假設
由于投擲距離受多個因素的影響,在剔除無效點后,假設投擲距離y與出手速度x1、出手角度x2、初始攻角x3具有如下關系:
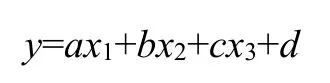
3.2 多元線性回歸方程系數的計算

3.3 回歸方程的檢驗
對此模型擬合的P值進行計算,此擬合結果為P=6.299×10-16,P<<0.000 1,說明本次擬合有效。
對此模型擬合的R相關系數進行計算,R=0.979 8≈1,接近1,置信度很高。
對此模型F值進行檢驗,F=307.803 1,F值越大,越能說明y與xi之間具有線性關系。
綜合上述三點可證明,多元線性回歸方程的假設成立。
3.4 偏回歸平方和Qi的比較
由于利用偏回歸平方和Qi可以衡量每個變量在回歸中所起的作用大小(即影響程度),設S回是p個變量所引起的回歸平方和,S回1是p-1 個變量所引起的回歸平方和(即除 去xi),則偏回歸平方 和Qi為Qi=S回-S回1=即去掉變量xi后,回歸平方和減少的量。
最終得出出手速度x1對投擲距離y的影響最大,且影響效果很強,出手角度x2也對投擲距離y有影響,但影響效果相對較弱,初始攻角x3對投擲距離y的影響相對最弱。

