數學本真教學

【摘 ? 要】數學本真教學是在余文森教授倡導的“讀思達”教學法下提出的教學主張，這一主張強調教學要基于學生的學情，追求真實有效的數學閱讀、獨立思考和個性表達，突出數學本源，并要著眼學生發展，探究數學真相，從而建構教材、課堂、學生三位一體的課堂基本框架。

【關鍵詞】讀思達;本真教學;課堂模式

福建師范大學余文森教授倡導的“讀思達教學法”，從閱讀、思考和表達三個層面對課堂教學提出新觀點、新理念。余教授指出：“教學過程就是學生的學習過程，學習過程即閱讀、思考、表達的過程，閱讀、思考、表達是教學的三個基本環節。學生只有經過這三個環節的相對完整的學習，才能把知識轉化、內化為素養，所以這是一種以學生學習為本位的讓核心素養落地的教學法。”“讀思達”是基本的教學方法，為數學本真教學（以下簡稱本真教學）的探索提供了理論支撐。

一、影響：“讀思達”對本真教學理論的發展

“讀思達”教學法是核心素養背景下，對“立德樹人”育人導向的踐行，對課程改革具有重要意義。

（一）發展本真教學理論

本真教學基于學情，關注數學教學的育人價值和實踐應用，注重培養學生學會閱讀，學會思考，清晰表達數量關系和數學模型。“讀思達”教學法倡導讓學生經歷完整的學習過程。個人閱讀、提出問題和學科表達，對“本真教學”具有較強的理論引領，豐富了本真數學的內涵：突出數學閱讀的地位和作用，準確把握學生的知識經驗，引導學生經歷知識發生發展的過程;凸顯思考，遵循學生的思維規律和認知特點，讓學生學會有邏輯地思考，創造性地思考;自主表達，學會個性表達數學理解和探究發現，引導學生用自己的語言表達數學規律和思維過程。“讀思達”教學法豐富了本真教學的理論內涵，把數學學科核心素養的培育落實在課堂教學中。

（二）形成數學本真教學模式

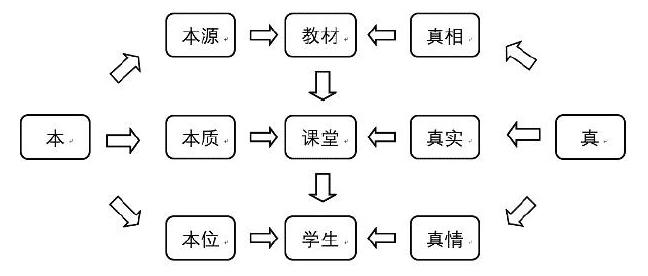
閱讀、思考、表達是素養本位教學法，是其他教學法研究的信號源和方向標。本真教學從教材、課堂和學生三個層面踐行“讀思達”，突出三個“重”：一是重教材閱讀，引導學生自主閱讀，讀懂教材，讀明思路，讀透思想;二是重課堂思考，課堂教學啟發學生獨立思考，養成良好的思考習慣;三是重學生表達，啟發學生用自己的思維探究數學，用自己的思考理解數學，用自己的語言表達數學。在讀、思、達三個階段中，形成本真教學模式（見下圖）。

（三） 指導本真教學課堂實踐

針對數學教學中弱化學生的數學閱讀和數學表達的現象，本真教學要突出閱讀與表達。數學閱讀包括讀懂知識、讀寬知識、讀透知識三個層次。讀懂知識，即要鼓勵學生課前預習，讀懂所學的知識內容，讀懂所介紹的方法和路徑，讀懂數學探究的過程，讀懂數學表達的呈現方式，等等。讀寬知識，即要多渠道收集相關知識，閱讀相關課外書籍，網絡查詢相關內容，多方獲取知識，體驗獲取知識方法的多元性。讀透知識，即讀出知識間的聯系，理解數學與生活的聯系，把握知識的研究方向，等等。數學表達的方式可以是語言表達、圖像表達、算式表達、操作表達、實驗表達等。教師要鼓勵學生結合自己的理解，學會多樣的表達方式，力求從數學角度理解知識，把握關系，呈現個性的表達方式。

二、導向：“讀思達”對本真教學方法的引領

本真教學在“讀思達”教學法理論引領下展開，讀是學習之本，思是教學之真，達是本真之宿。

（一）讀是教學之本

閱讀的本質是信息的吸收。數學閱讀的弱化導致學生的信息輸入不足，直接影響學生對教學內容的接受和理解。因此，本真教學強調數學閱讀，注重培養學生多渠道獲取知識的能力，主要有課前預習、課中自學和課后研學。課前預習側重閱讀書本知識，課中自學重點讀懂獲取知識的方法指導，課后研學是拓寬數學閱讀。通過數學閱讀，讓學生主動提出問題、主動探究知識本源，把握知識生長點、知識連接點、知識結構點，從本源上理解數學。

（二）思是教學之真

本真教學追求理性思維，培養學生學會思考。思是教學之真，教學的根本任務不僅是記憶、理解和掌握知識，而且要培養學生的思考力、判斷力和鑒賞力。因此，培養和訓練學生的數學思維是教學的主要任務，要注重引導學生在閱讀理解的基礎上，經歷真實的探究過程，要關注學生的思考過程和認知過程，培養學生創造性思維的發展。本真教學中，思考應貫穿于教學的全過程，是教學的出發點，也是教學的落腳點。

（三）達是本真之宿

數學表達是本真教學的歸宿。本真教學關注核心素養的育人目標，確立了學習的根本任務是學會閱讀、學會思考、學會表達。學習過程中學生的主動閱讀、主動探究，其最終回歸點就是數學表達，數學表達是學生閱讀理解的一種真實展現。數學表達包括語言表達、算式表達、符號表達、圖像表達、關系表達等，通過表達，學生達到能力的升華。數學表達是本真教學的根本任務和價值導向，要讓學生學會在閱讀理解的基礎上表達自己的觀點和看法。

三、作用：“讀思達”對本真教學實踐的指導

“讀思達”倡導讀、思、達三者有機融合，相互促進，其中讀是基礎，思是關鍵，達是核心，三位一體。

（一）增進“讀”與“思”的融會

數學閱讀應伴隨思考，閱讀的過程也是思考、反思和推理的過程，是讀與思的融合。本真教學倡導課前閱讀、課中自學、課后研學。課前閱讀帶著導學問題，課中自學帶著明確要求，課后研學帶著數學問題，主動探究、主動學習。

以人教版四年級下冊“三角形內角和”一課為例，課前預習導思：什么是三角形的內角和？不同類型的三角形內角和相等嗎？三角形內角和有什么規律？你想怎么研究三角形內角和？除了了解課本上介紹的方法外，你還知道其他方法嗎？讓學生帶著問題閱讀，讓數學閱讀有思考。課中自學導思：教材中的“畫幾個不同類型的三角形。量一量，算一算，三角形3個內角的和各是多少度”你怎么理解？“我的這個直角三角形的內角和大約是180°”“我的是銳角三角形，也是……”讓你想到什么？是不是所有的三角形內角和都是180°？你想怎么驗證？課本介紹的這種方法是否可以驗證任何三角形？再次閱讀課本，思考會更加深刻，探究會更加有效，使得數學學習更具合理性和實效性。課后研學激思：三角形內角和的探究方法有什么值得借鑒的？四邊形的內角和是多少？五邊形、六邊形、N邊形呢？這些圖形的內角和有怎樣的規律等等，引導學生繼續探究計算多邊形內角和方法間的聯系（見下圖）。

（二）促進“思”與“達”的貫通

本真教學著眼學生需要，立足課堂真實，探究數學真相，還原數學本來的呈現方式，顯現學生真實的思考過程和真實的數學表達。學生可以借助圖像、符號、算式及語言表達他們的探究過程，以及他們對知識的理解，實現思與達的貫通，讓學習真正發生。

以“商的變化規律”為例（見下圖），可以引導學生回憶“積的變化規律”，促發學生思考：商的變化規律可能是什么？引導學生提出猜想：猜想一，除數不變，被除數擴大（縮小）幾倍，商也擴大（縮小）幾倍;猜想二，被除數不變，除數擴大（縮小）幾倍，商也擴大（縮小）幾倍。數學需要有理有據的思考，有了猜想，還要有驗證，有推理，它們是更深層次的思考。猜想一借助舉例，可以嘗試讓學生自主發現規律，學生也可以借助“積的變化規律”進行語言表達。猜想二是教學的難點，用舉例驗證的方法也可以發現規律：被除數不變，除數擴大（縮小）幾倍，商反而縮小（擴大）幾倍。反思猜想與發現之間的不同，可以進一步啟發學生思考：為什么除數的擴大（縮小）幾倍，商反而縮小（擴大）幾倍？可以讓學生借助除法意義的理解，嘗試自主表達：在除法里，除數表示分的份數，除數擴大（縮小）意味著分的份數多（少）了，當然每一份就少（多）了。在兩個活動經驗的基礎上，啟發學生進一步思考：被除數和除數怎樣變化，商才能不變？學生結合思維活動經驗，提出猜想三：被除數和除數同時乘以或除以一個不為0的數，商不變。從猜想一、猜想二到猜想三的提出和驗證，讓學生在猜想中暴露思維，在驗證中完善表達。在探究中，學生運用猜想、驗證、觀察、比較、推理等思維方式，實現了真正意義上的數學建構。

（三）推進“讀思達”的深化

本真教學吸取“讀思達”理論的精髓，加強學生的數學閱讀，激發數學思考，學會數學表達，培養全面發展的人。

以人教版教材“平行四邊形的認識”為例，由于學生對平行四邊形的了解經驗先于認識，思維定式影響他們對平行四邊形特征的理解。如何引導學生認識平行四邊形？教師可以從本源上尋找學習切入點，先讓學生尋找生活中的平行四邊形物體，并嘗試把平行四邊形畫出來。這里的“畫”出來，就是抽象，畫的過程是經驗和思維的激活，也就是表達圖形的特征。當然，停留這一層面的教學仍然是淺層次的認知，需要進一步的數學思考和語言表達：平行四邊形有什么特征呢？怎么驗證你的發現？引導學生進入探究環節，借助測量工具，如直尺、三角尺等進行實踐測量、驗證，經歷從感性到理性，從片面到全面，從現象到本質的探究過程。在表達層面，需要培養學生有依據的數學表達，如經過測量發現平行四邊形對邊分別相等，經過平移發現平行四邊形對邊分別平行……進一步培養學生數學表達的條理性和準確性，最后理解平行四邊形的定義“兩組對邊分別平行的四邊形，叫作平行四邊形”。

本真數學教學需要在“讀思達”理論引領下不斷豐富和發展，本著務實求真的科學態度探究本真數學課堂教學模式，推進基礎教育課程的改革。

參考文獻：

[1]余文森.核心素養導向的課堂教學[M].上海：上海教育出版社，2017.

[2]余文森.論核心素養導向的三大教學觀[J].當代教育與文化，2019（3）.

[3]余文森.教學主張：打開專業成長的“天眼”[J].人民教育，2015（3）.

[4]唐少雄.“本真數學”教學主張及構建實踐[J].小學數學教與學，2019（9）.

[5]尚家茗.“讀思達”教學法之思與行[J].河南教育，2019（3）.

（福建省莆田市秀嶼區教師進修學校 ? 351146）