基于共旋法與穩定函數的幾何非線性平面梁單元

鄧繼華，譚建平，譚 平，田仲初

(1. 長沙理工大學土木工程學院，長沙 410076；2. 廣州大學工程抗震研究中心，廣州 510405)

隨著計算機軟硬件技術的發展，基于非線性有限元開展結構破壞乃至失效倒塌分析已經成為可能[1 ? 2]，這其中研究開發出各種高效精確的非線性單元模型和算法是基礎和前提[3 ? 5]。對于幾何非線性梁單元，許多學者從考慮應變的高階項推導精確的單元切線剛度矩陣、桿端力與變形后單元坐標轉換矩陣的精確計算等入手，進行了卓有成效的研究[4, 6]。在各種幾何非線性有限元列式中，共旋坐標(CR)法認為結構的幾何非線性主要由結構大位移引起，因此在分析中每一個單元都建立一個共旋坐標系(局部坐標系)，該坐標系隨單元位移發生平移和轉動，該坐標系下單元的純變形可以通過扣除單元剛體平移和轉動而得到，相應可求得單元切線剛度矩陣和抗力，再通過變換的坐標轉換矩陣將其轉換到結構坐標系下，此過程中幾何非線性效應被自動計入[7 ? 9]。研究表明，基于共旋坐標法研究幾何非線性，不僅具有列式簡單、計算準確，以及適用于桿、梁、平面、殼、實體單元等各類型單元的優點[10 ? 14]，而且能將幾何與材料非線性脫藕，即材料非線性在局部坐標系內考慮，幾何非線性則通過局部坐標系與結構坐標系之間的轉換予以實現[15?16]。對于梁單元而言，除了大位移能引起幾何非線性以外，梁-柱效應也是引起幾何非線性的一個重要因素[17]，這其中采用能考慮構件軸力與彎矩相互作用的穩定函數[18 ? 19]來考慮梁柱效應是一種最精確的方法[20 ? 21]，實際工程分析中常采用的幾何剛度矩陣實質是將穩定函數法表達的單元剛度矩陣用級數展開，取其一階近似而得到[22]。但應指出的是，以往基于穩定函數法的研究采用的有限元列式一般為T.L或U.L 列式，筆者尚未見到將穩定函數法與共旋坐標(CR)法結合起來進行幾何非線性平面梁單元的研究。因此，本文基于共旋坐標法，在局部坐標系下分離單元剛體位移和變形，采用穩定函數考慮梁柱效應；再基于結構坐標系與局部坐標系下節點力之間及節點位移之間的總量關系及微分導出的增量關系，獲得平面梁單元在結構坐標系下的全量平衡方程和切線剛度矩陣；在此基礎上根據帶鉸梁端彎矩為零的受力特征，導出了能考慮梁端帶鉸的單元切線剛度矩陣。最后通過數個經典算例對本文算法及程序進行了較全面和嚴格的檢驗。

1 平面梁單元切線剛度矩陣

如圖1(a)、圖1(b)所示分別為初始時刻和計算t時刻的平面梁單元，XY為結構坐標系，xy為單元的共旋坐標系，它具有隨單元變形而轉動的特點，在運動中始終以節點i為原點，以節點i到j的連線方向為x軸，y軸則由x軸按逆時鐘方向旋轉90°形成。

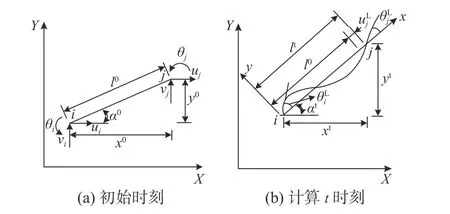
圖1 變形前后平面梁單元Fig. 1 Plane beam element before and after deformation

初始時刻設單元在結構坐標系下水平及豎向的投影長度為x0和y0，在計算t時刻結構坐標系中的位移向量d=[ui viθi uj vjθj]T，在共旋坐標系中的位移向量dL=[uLi vLiθiLuLj vLjθLj]T，聯立圖1(a)、圖1(b)，有：

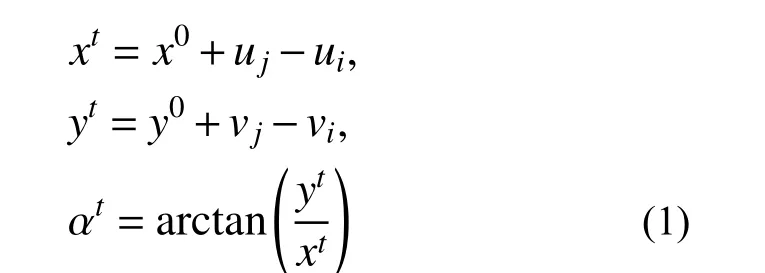
平面梁單元在共旋坐標系中的節點位移為：

其中：

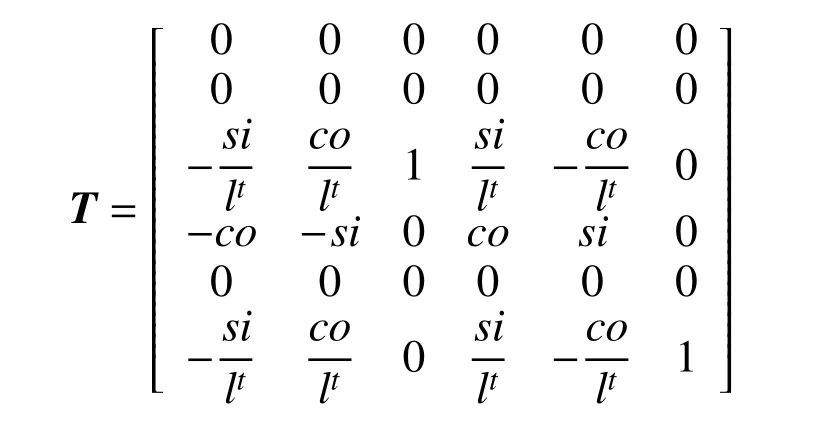
式中：si=sinαt,co=cosαt。

圖2(a)、圖2(b)所示分別為梁單元及微段的受力平衡情況。

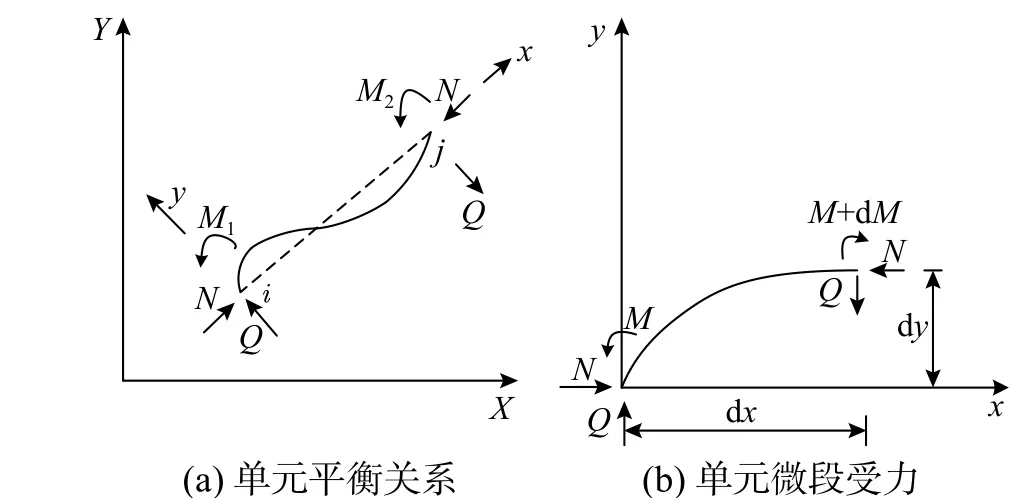
圖2 梁單元及微段Fig. 2 beam element and micro-segment

對式(11)進行與單元受拉時同樣的推導，可得到與式(9)相同的表達式，只是各參數s、c、k、ω的計算式變成以下形式：

kT的具體表達式較繁瑣，限于篇幅此處未列出。

聯立式(19)和式(20)，可將式(17)寫成：

2 梁端帶鉸時的單元切線剛度矩陣

3 非線性方程組求解和計算流程

非線性方程組的增量法求解主要有荷載增量法和位移增量法[23]。理論上而言，荷載增量法只能計算出荷載-位移曲線的上升段，而位移增量法能計算荷載-位移曲線的下降段，從而能獲得極限荷載值與位移值；但在實際計算中發現，由于在荷載-位移曲線的頂點附近結構切線剛度接近奇異，即使采用位移增量法，非線性計算也很難收斂。鑒于此，很多文獻都大力推薦弧長增量法，文獻[24]對傳統弧長增量法[25]研究后認為，該方法能順利進行的前提是必須對結構的特性有深刻的了解并進行復雜的試算，顯然這會給分析工作帶來極大困難和不便；因此，該文獻在傳統弧長增量法的基礎上提出一種如圖3 所示的基于牛頓-拉菲遜法的投影增量法，該方法能有效克服傳統弧長增量法的上述缺點，且該方法收斂速度要稍快，計算量也略小，本文采用該方法進行非線性方程組的求解。

本文非線性計算流程如下：

1)根據式(2)由上一荷載步末單元i、j節點在結構坐標系下的總位移向量d求出共旋坐標系下的節點位移向量dL；

2)由式(13)中最后一行單元軸力N的計算式得到N，再根據軸力N是受拉還是受壓分別基于式(10)或式(12)計算參數s、c、k、ω，進而根據式(9)得到單元彎矩Mi和Mj；

3)根據式(13)可得到單元在共旋坐標系下的桿端力向量為f；

4)由式(4)和式(16)分別計算矩陣T和t；

5)由式(19)計算Kn，再由式(22)得到單元在結構坐標系下的切線剛度矩陣K；

6)由式(16)得到單元在結構坐標系下的節點抗力向量F；

7)對所有單元重復步驟1)～步驟6)，基于常規的“對號入座”原則疊加形成結構總剛矩陣和總抗力矩陣；

8)由總抗力矩陣與總荷載矩陣之差形成不平衡力矩陣作為非線性平衡方程的右端項，解方程得到增量位移矩陣 ?d，與前述總位移向量d疊加形成新的總位移向量d；

9)判斷是否收斂，如是，轉至下一個荷載步；如否，進行下一輪迭代計算。

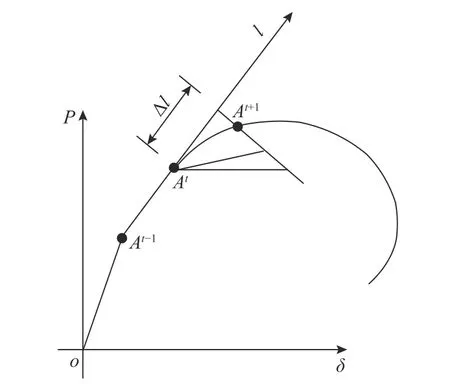
圖3 投影增量法示意Fig. 3 Projection increment method

4 算例分析

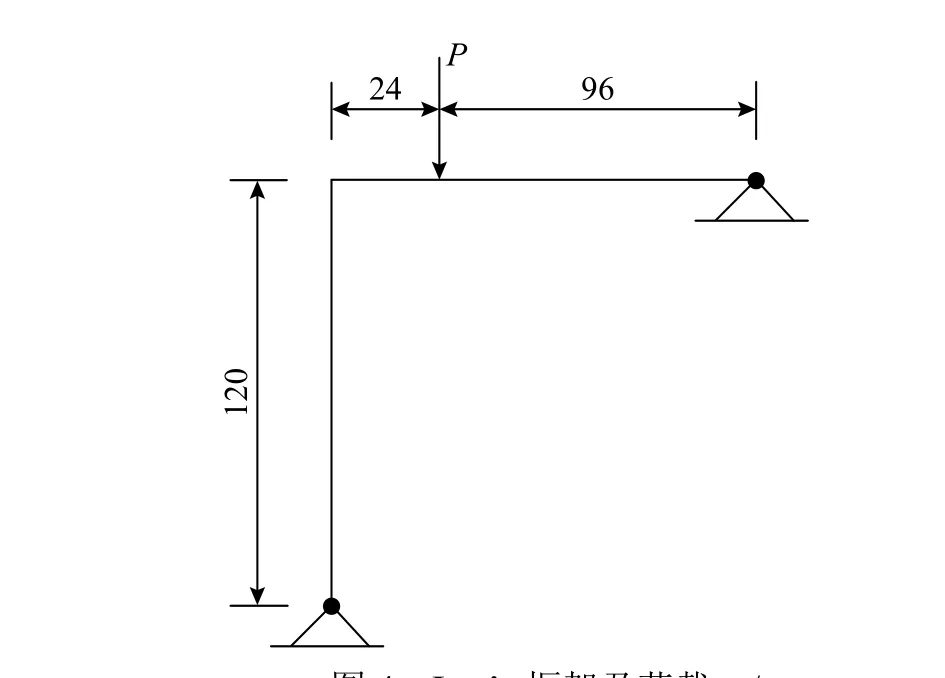
圖4 Lee’s 框架及荷載 /cm Fig. 4 Lee’s frame geometry and loading

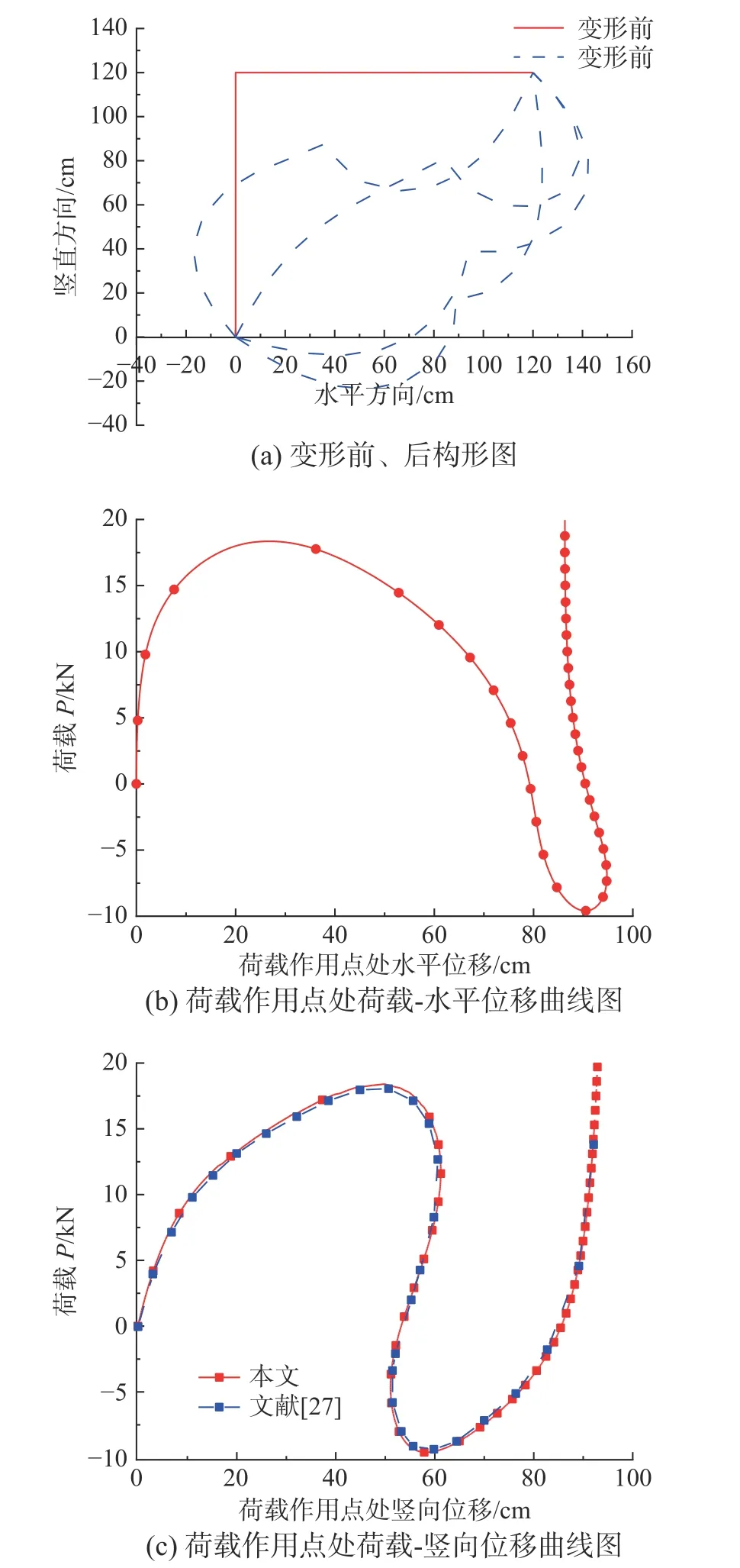
圖5 Lee’s 框架Fig. 5 Lee’s frame

采用3 個經典算例對本文算法及程序從正確性、計算效率及精度方面進行較全面和嚴格的檢驗。算例1. 如圖4 所示為Lee’s 框架[26]，材料及幾何參數如下：線彈性模量E=7060.8 kN/m2，梁和柱具有同樣的截面，且截面面積為6 cm2，慣性矩為2 cm4，對結構進行幾何非線性分析，分析中柱均分為8 個單元，荷載作用點左邊梁均分為2 個單元，右邊梁均分為6 個單元，圖5(a)所示為框架的初始構型以及不同變形時刻的構型，圖5(b)、圖5(c)所示分別為荷載作用點處荷載-水平位移及荷載-豎向位移曲線，可看出與相關文獻[27]的計算結果很吻合(該文獻未提供荷載-水平位移曲線)。算例2 . 如圖6 所示懸臂梁，集中荷載P=35 kN作用在自由端，梁跨為L=100 m、彎曲剛度為EI=3.5×104kN·m2、梁端水平位移為u、垂直位移為w、轉角為θ，對本算例按以下兩種方法求解：

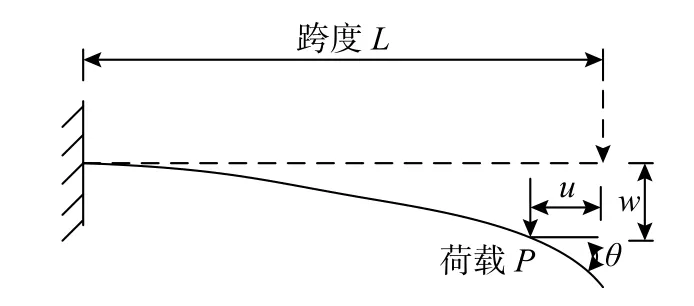
圖6 端部承受集中荷載的懸臂梁Fig. 6 Cantilever subjected to concentrated load at free end

方法1. 采用本文算法研制的程序進行計算；

方法2. 按文獻[11]和文獻[28](文獻[28]就是將文獻[11]的算法從平面梁延伸到空間梁)的方法進行計算，即共旋坐標系下的桿端力就由節點位移(去除了剛體位移)與小位移線彈性剛度矩陣相乘得到。

為使計算結果具有可比性，兩個程序采用的方程組求解方法、數據精度及收斂精度標準等都完全相同，方法2 中桿端力也是基于全量計算，詳見文獻[11]及文獻[28]。

兩種方法得到的計算結果及比較見表1 和表2，解析解見文獻[29]。可以看出，無論是從非線性計算能力、精度還是穩定性方面，方法1 均優于方法2(方法2 在劃分為1 個單元及4 個荷載步情況下還出現錯誤的收斂解)；還可以看出，由于方法1 與方法2 中桿端力的計算均是基于全量計算，所以在單元數劃分固定的前提下，計算精度與荷載步數無關。

表1 懸臂梁自由端的位移Table 1 Displacement of cantilever at free end

表2 計算誤差 /(%)Table 2 Calculation error

算例3. 如圖7(a)所示，一對拉力2P作用于鉸接方棱形框架的對角點，各項幾何、材料參數及位移變量詳見圖7，EI為桿件的抗彎剛度。

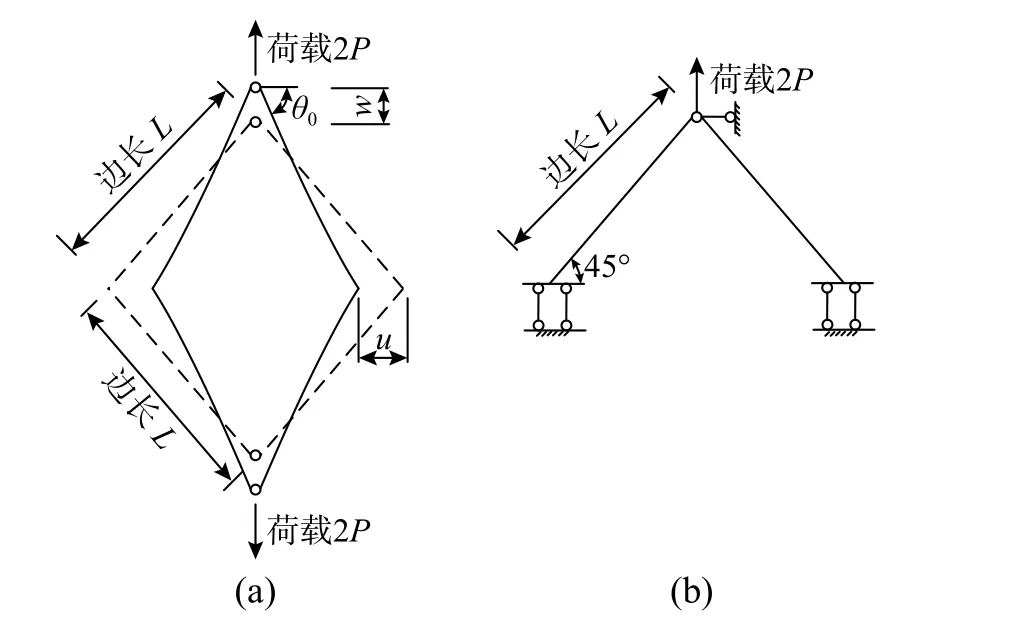
圖7 對角點受拉力作用時的鉸接方棱形框架Fig. 7 Diamond-shaped frame under a pare of opposite concentrated tensions in opposite angles

為驗證本文所導出的帶鉸梁單元模型，基于荷載及結構對稱的特征，取圖7(b)所示的1/2 結構進行計算，按每根桿件分成1、2、3 和4 個單元(中間鉸左、右兩個相鄰單元類型選用本文推導的帶鉸單元)，在荷載參數PL2/EI=10 時所得的計算結果如表3 所示，其中解析解見文獻[29]。從表3可看出，計算結果收斂非常好，如按工程精度誤差不超過5%的要求，則每根桿件劃分成3 個單元就已經足夠。

表3 鉸接方棱形框架位移Table 3 Displacement of diamond-shaped frame

5 結論

本文在局部坐標系下采用穩定函數考慮P-δ效應，再基于結構坐標系與局部坐標系下節點力之間及節點位移之間的總量關系及微分導出的增量關系，獲得平面梁單元在結構坐標系下的切線剛度矩陣，同時還獲得單元桿端力的全量算法；在此基礎上，根據帶鉸梁端彎矩為零的受力特征，導出了能考慮梁端帶鉸的單元切線剛度矩陣表達式。多個算例表明本文算法是正確的，相對于已有文獻算法，本文算法在非線性計算能力、精度以及穩定性方面均占有一定優勢，可用于平面桿系結構的幾何非線性分析。