鋼-超高性能混凝土組合箱梁彈性彎曲性能試驗研究及解析解

樊健生，王 哲，楊 松，陳 釩，丁 然

(1. 清華大學土木工程系，北京 100084；2. 清華大學土木工程安全與耐久教育部重點實驗室，北京 100084；3. 清華大學水利水電工程系，北京 100084；4. 中電建路橋集團有限公司，北京 100048)

近幾十年來，我國建成了眾多的大跨徑橋梁[1]，其中包括有港珠澳大橋等超級工程。然而，工程實踐表明，對于常用的正交異性鋼橋面系或鋼-混凝土組合橋面系，橋面系病害或橋面系自重過大制約著橋梁跨徑的提高[2]。

UHPC 作為一種力學性能優異的新型混凝土材料，近年來在結構工程尤其是橋梁工程中得到越來越多的應用[3 ? 9]。將UHPC 作為橋面板，相比于正交異性鋼橋面，其抗疲勞性能更優，能夠降低疲勞病害；相比于普通混凝土橋面板，UHPC橋面板可做到更小的厚度，使得橋面系自重降低[10]。因此本文研究一種鋼槽梁+UHPC 橋面板的新型組合橋面系，該橋面系有望應用于更大跨徑的橋梁中。

對于鋼-普通混凝土組合箱梁橋面系，國內外已有較多研究[11 ? 19]。主要針對組合箱梁的整體抗彎承載力(加載點必須位于鋼梁正上方)、界面滑移、剪力滯后效應、施工技術等。對于鋼-普通混凝土組合梁的理論分析模型，Newmark 等[20]于1951年提出了考慮界面滑移效應的組合梁解析解；Nie等[21]深入研究了界面滑移效應對組合梁剛度的影響；孫飛飛等[22]推導了同時考慮剪切變形、滑移及剪力滯的工字鋼組合梁的解析解，其模型中并未考慮鋼梁的剪切翹曲；周旺保[23]推導了考慮上述效應的組合箱梁的解析解，但其模型中的鋼腹板剪切變形僅與剪力荷載成正比，并未考慮腹板剪切變形的不均勻分布。

相比于鋼-混凝土組合橋面系，已有的針對鋼-UHPC 組合橋面系的研究偏少。田啟賢等[24]針對正交異性鋼箱梁+UHPC 板的組合橋面系開展了試驗研究，包括鋼-UHPC 組合梁和鋼-UHPC 組合板的靜力性能試驗研究，以及組合橋面系的疲勞性能試驗研究，結果表明該類型橋面系靜力性能及疲勞性能良好。Yuan 等[25]同樣針對該類型的橋面系的局部組合梁開展了疲勞性能試驗研究，結果表明鋪設UHPC 板顯著降低了鋼頂板的應力水平。邵旭東等[26 ? 27]采用試驗和數值模擬方法研究了鋼-UHPC 組合板的整體抗彎及界面抗剪性能。劉誠等[28]研究了鋼-UHPC 組合梁中栓釘連接件的疲勞性能。以上研究中主要研究對象為正交異性鋼箱梁+UHPC 板的組合橋面系，其中的試驗研究大多為梁、板等局部構件層面，橋梁節段尺度的試驗較少；研究方法主要為試驗研究和數值模擬，理論解析研究較少。

本文針對鋼槽梁+UHPC 板的組合箱梁橋面系開展了大比例節段模型試驗，關注組合橋面系整體抗彎性能，并針對彈性受力階段的組合箱梁建立同時考慮剪力滯后、滑移效應以及鋼腹板剪切變形的分析模型，并推導得出解析解，為新型橋面系的工程應用提供參考。

1 試驗方案設計

1.1 試件設計

某實際工程橋梁橋面系方案中，鋼腹板間距27 m、橫隔板間距3 m、梁高3 m。在該橋面系方案的基礎上，共設計了2 組鋼-UHPC 組合箱梁構件，編號為CDS-1 和CDS-2，試件整體縮尺比例約為1∶3。然而縮尺后的橋面寬度尺寸仍較大，本試驗重點研究橋面系縱向受力行為，考慮實驗室場地及加載能力的限制，同時兼顧試驗目標，最終減小腹板間距至3 m，使得四邊約束的UHPC板仍滿足單向板條件。

兩個組合箱梁試件均采用UHPC 板+鋼槽梁的截面形式，鋼槽梁設計相同，變化參數為UHPC板厚度，如圖1 所示。鋼槽梁縱向總長度為3.2 m，橫向寬度為3.16 m，高度為1 m，腹板采用8 mm厚鋼板，其余鋼板均為6 mm 厚。箱梁腹板中心間距為3 m，設有水平及豎直加勁肋；橫隔板間距為1 m，同樣設置了雙向加勁肋。相鄰橫隔板之間的底板中間區域作開洞處理，目的是方便觀測UHPC 板底的開裂行為。

UHPC 板縱向長3.2 m，橫向寬4 m，厚度分別為60 mm(CDS-1)和90 mm(CDS-2)。UHPC 板與鋼槽梁的連接采用栓釘連接件，栓釘直徑13 mm、高35 mm，焊接在腹板上翼緣(布置3 列)及橫隔板上翼緣(布置1 列)。UHPC 板中配置雙層鋼筋網，縱橫鋼筋均為 8@100，采用HRB400 級螺紋鋼筋，兩層鋼筋網橫筋在內、縱筋在外，保護層厚度為8 mm。

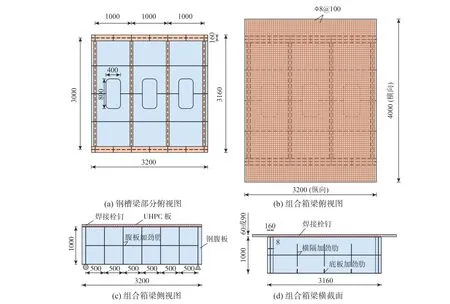
圖1 試件設計 /mm Fig. 1 Test specimen design

兩個組合箱梁試件的主要設計參數匯總如表1所示。

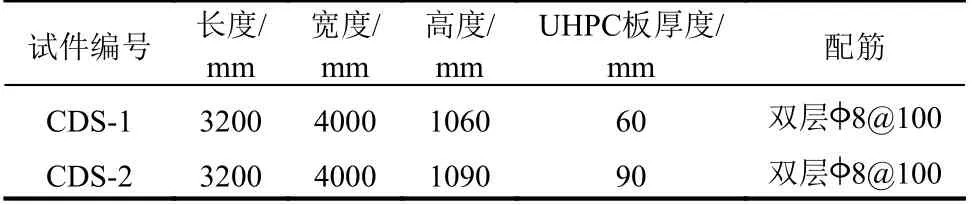
表1 試件主要參數Table 1 Parameters of specimens

1.2 材料性能

本文中采用的UHPC 配合比如表2 所示。鋼纖維選用長13 mm、直徑為0.2 mm 的平直型鋼纖維，其體積摻量為2.5%。UHPC 采用高溫蒸汽養護，具體步驟為：澆筑結束后覆膜養護48 h，然后放入養護室中90 ℃高溫蒸養48 h。UHPC 抗壓強度采用邊長100 mm 的立方體試塊測得，并按照折減系數0.9 換算為軸心抗壓強度[29]；UHPC 軸心抗拉強度采用狗骨試件[30]測得。

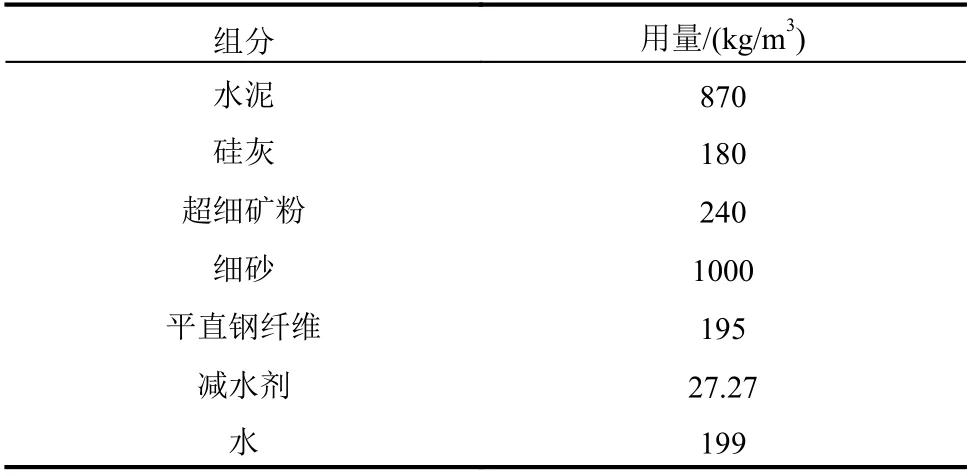
表2 UHPC 配合比Table 2 Mix proportions of UHPC

材性試驗測得的UHPC、鋼筋及鋼板的主要力學性能見表3。

1.3 試驗裝置及加載方案

試驗重點關注組合箱梁試件的縱向受力性能，考慮到實驗室加載條件，設計縱向對邊簡支邊界條件，在兩端橫隔板正下方設置支座。

CDS-1 和CDS-2 加載裝置如圖2 所示。加載位置位于兩側腹板跨中正上方，加載點位置墊有100 mm×100 mm 鋼墊板，最大荷載基于精細有限元模型結果確定，不超過有限元模型中鋼板屈服時荷載的85%，且試驗中持續觀測試件各處應變達到全程控制。

為了保證兩處加載點的荷載一致，兩個千斤頂共用同一液壓油路。

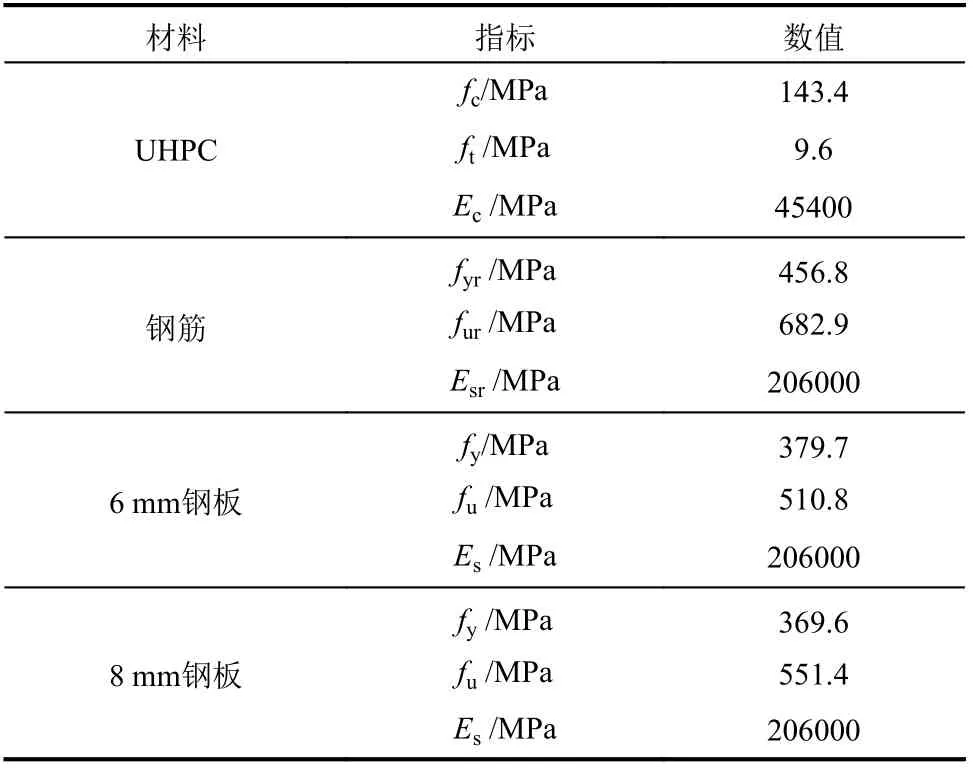
表3 材料力學性能Table 3 Material properties

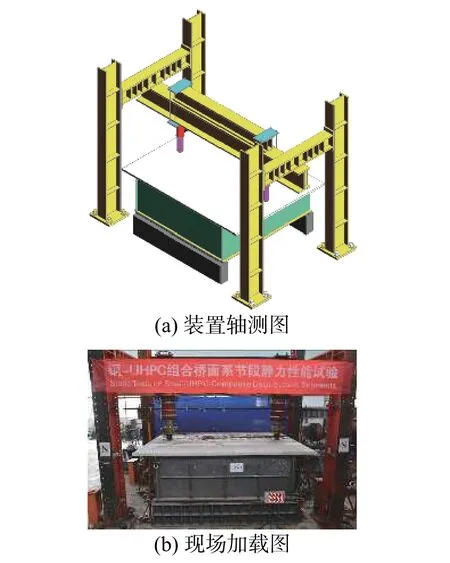
圖2 加載示意圖Fig. 2 Test setup

1.4 測點布置及量測方案

測點布置如圖3 所示。兩個試件的測點布置一致。

2 試驗結果及分析

2.1 荷載-撓度曲線

為了保證試件處于彈性階段并且得到可靠的試驗數據，試驗加載至1000 kN(兩個千斤頂各500 kN)停止。試驗測得的總荷載-UHPC 板跨中撓度曲線及總荷載-鋼梁跨中撓度曲線如圖4 所示。由圖可知，荷載-撓度曲線基本均為直線，試件剛度未降低，這表明材料整體處于彈性范圍內。由于加載點位于鋼梁腹板正上方，橫向UHPC 板中點的撓度略低于鋼梁腹板處撓度。

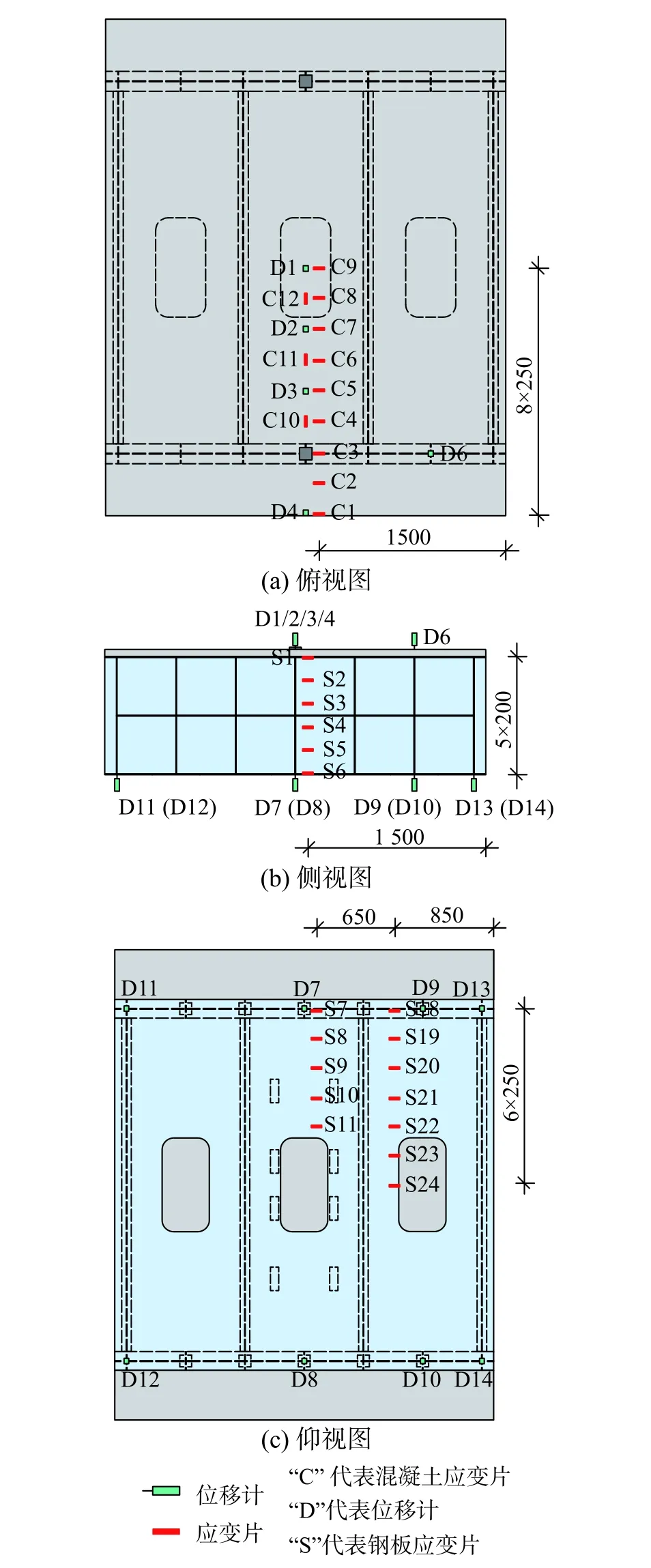
圖3 測點布置圖 /mm Fig. 3 Arrangement of measurement devices

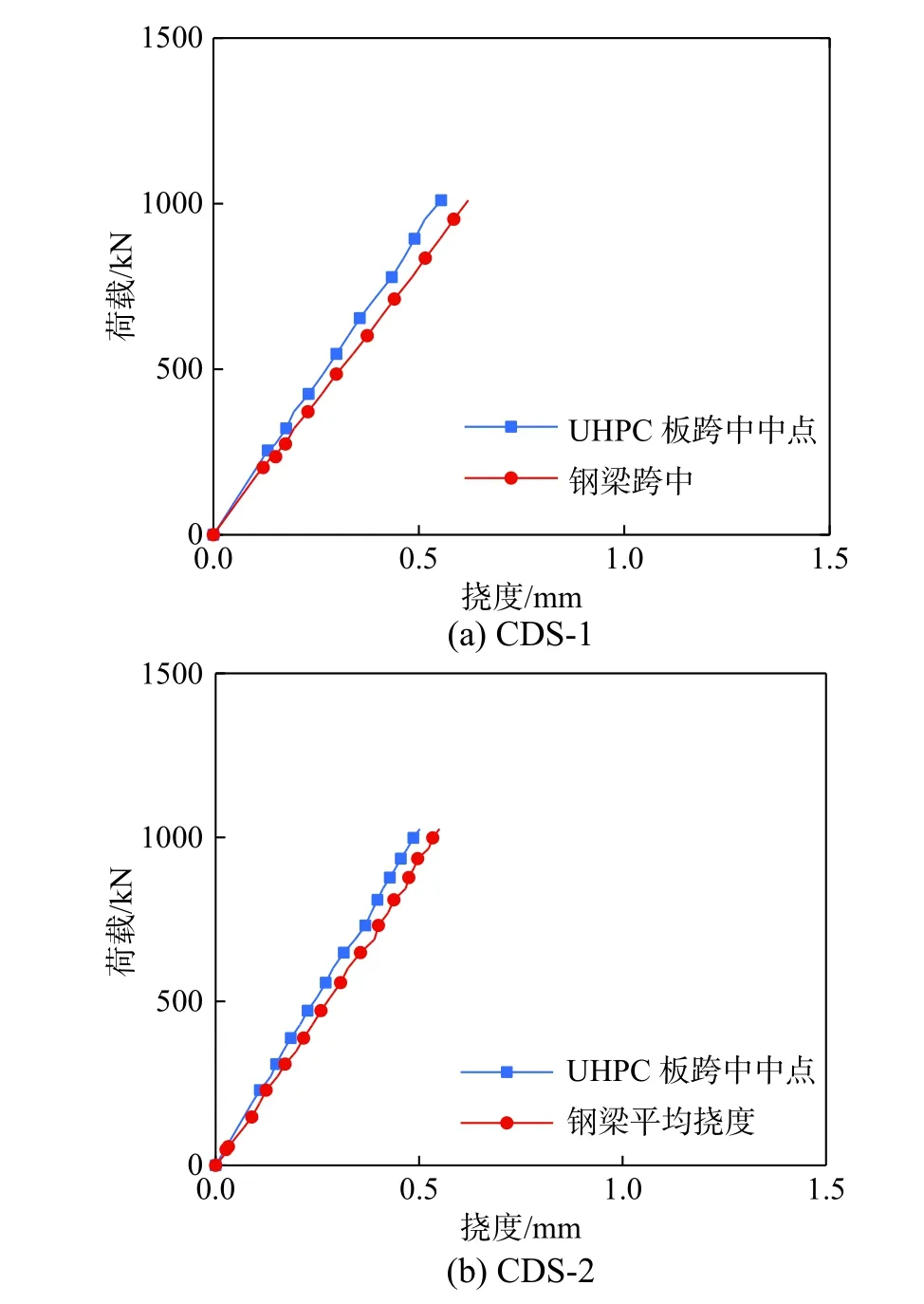
圖4 荷載-撓度曲線Fig. 4 Load-deflection curves

試件的撓度結果列于表4，可知CDS-2 的UHPC板跨中撓度及鋼梁跨中撓度均低于CDS-1。

表4 試件撓度Table 4 Deflection of specimens

2.2 跨中撓度分布

試驗中測量了跨中截面多個測點的撓度，撓度沿橫向分布的形式如圖5 所示。可見加載點撓度略高于其余測點，并且距離加載點越遠，撓度相對越小，但是不同測點間的差值較小，后文進行簡化分析時可忽略該差異。

2.3 跨中應變分布曲線

試件主要在跨中附近截面布置了應變片，對于UHPC 板及鋼梁底板的縱向應變，其橫向分布如圖6 所示。由于存在剪力滯后效應，鋼腹板附近的應變較大，應變隨著距鋼腹板距離的增大而減小，截面最大壓應變與最小壓應變之比約為5～7。由圖可知，跨中截面CDS-2 的UHPC 板頂壓應變明顯低于CDS-1，而鋼底板應變較為接近，規律并不明顯，有待理論解析解的進一步對比。

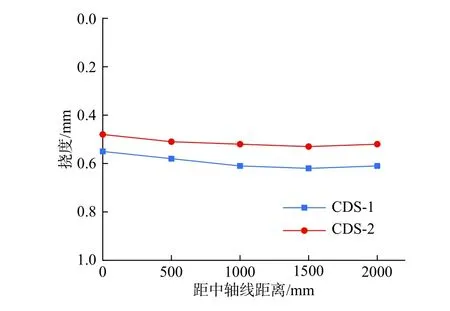
圖5 跨中撓度橫向分布Fig. 5 Transverse distributions of midspan deflections

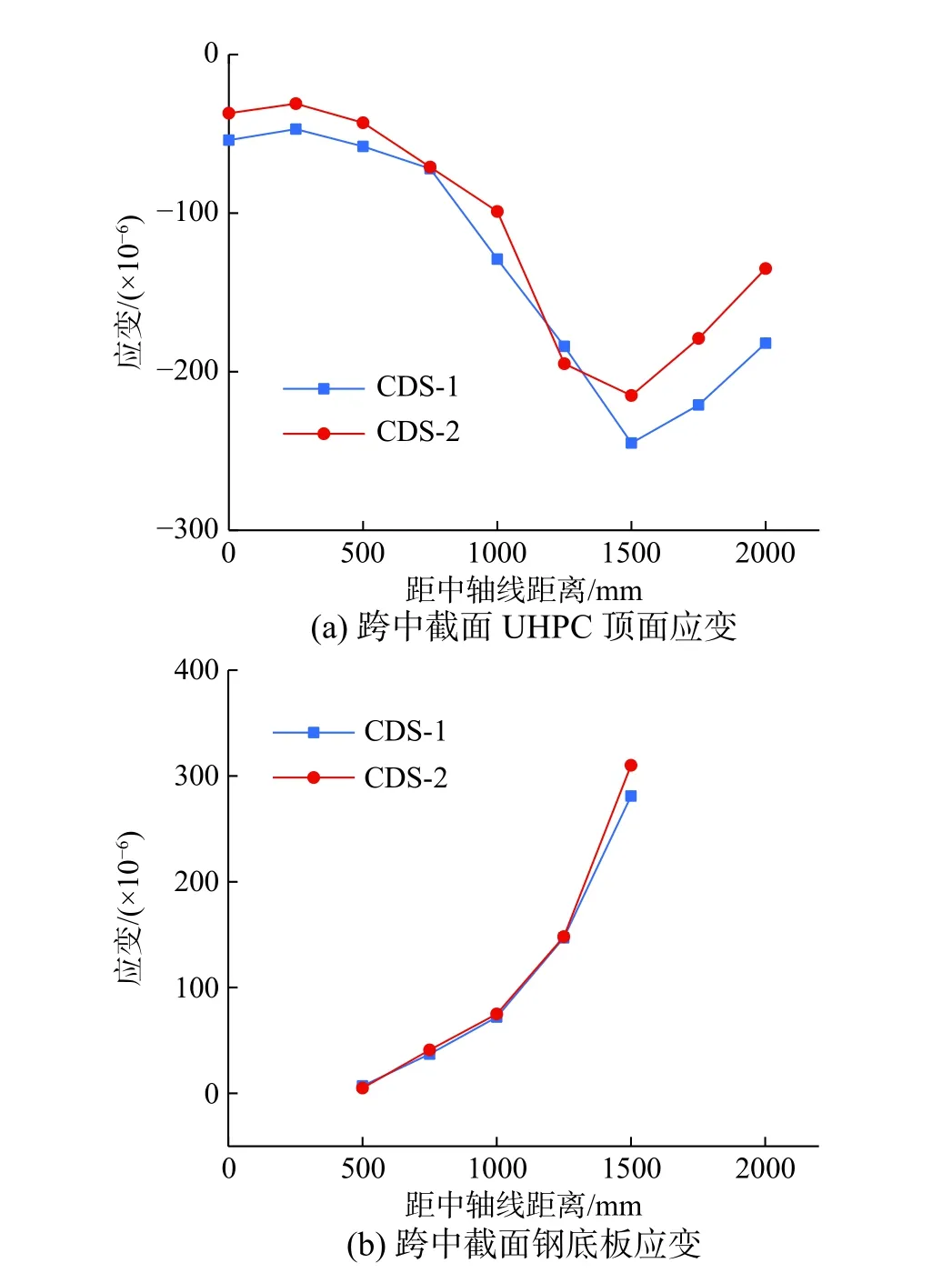
圖6 縱向應變的橫向分布Fig. 6 Transverse distributions of longitudinal strains

3 組合箱梁解析解

基于本文試驗，建立考慮剪力滯后、界面滑移效應以及鋼腹板剪切變形的組合箱梁分析模型。

3.1 基本假定

本文后續分析的開展基于以下假定：

1)由于混凝土板的厚度相對于其他方向的尺寸一般較小，因此對于混凝土板忽略其面外剪切變形；

2)鋼梁上翼緣尺寸相對較小，將其與鋼腹板統一考慮；

3)分析結構在彈性階段的變形，混凝土、鋼材、界面連接件的本構均為線彈性、位移可簡單疊加；

4)忽略混凝土板與鋼梁之間的豎向分離；

5)混凝土板的變形與鋼梁的變形分別滿足平截面；

6)忽略鋼腹板剪切變形對于界面滑移的影響。

3.2 分析模型

針對如圖7 所示的常見的鋼槽梁+混凝土板的組合箱梁截面進行分析，圖中b1、b2、b3、b4、tc、t1、t2、t3、hw分別表示鋼腹板間混凝土板寬度的一半、懸臂混凝土板的寬度、鋼腹板間鋼底板寬度的一半、鋼梁上翼緣寬度、混凝土板厚度、鋼梁上翼緣厚度、鋼腹板厚度、鋼底板厚度和鋼腹板高度。

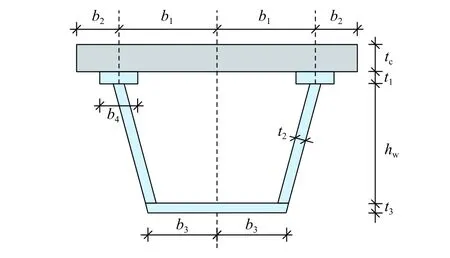
圖7 典型組合箱梁截面Fig. 7 Typical section of composite box girder

取組合箱梁中的微單元，分析其變形特征，單元變形前后如圖8 所示。圖中oc、ocs、os、osb分別表示混凝土板形心軸位置、組合換算截面中和軸位置、鋼梁形心軸位置、鋼底板形心軸位置，hc、hs分別表示混凝土形心軸和鋼梁形心軸距組合換算截面中和軸的距離，hb、hsu分別表示鋼梁形心軸距鋼底板形心軸和組合梁界面的距離。建立如圖8 所示的直角坐標系，x軸平行于組合梁長度方向，以支座位置為零點，且經過ocs；z軸垂直于混凝土板平面，且正方向為oc指向os；y軸以鋼梁對稱軸平面的位置為零點。

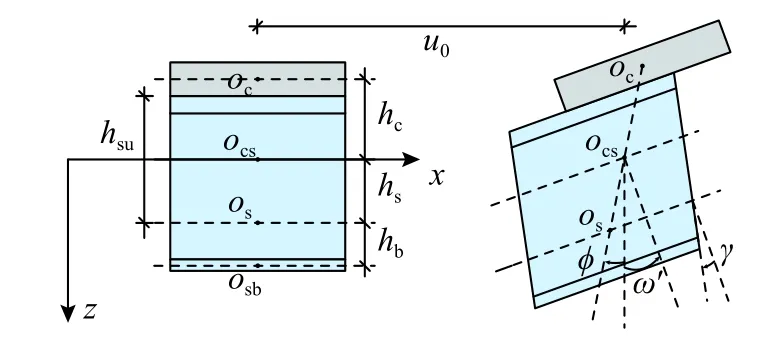
圖8 分析模型Fig. 8 Analytical model

在豎向荷載作用下，組合箱梁發生變形，組合箱梁任意一點的位移主要由界面滑移導致的位移、組合箱梁撓曲導致的位移和剪切變形(包括翼板剪力滯后以及鋼腹板剪切)導致的位移三部分組成。假設ocos在xz平面內的轉角為 ?(順時針為正)，組合梁豎向撓度為ω(與z軸反向)，鋼梁在xz平面內的剪切應變為γ(順時針為正)，xy平面內的剪力滯翹曲位移(與x軸同向)強度函數為f(x)、翹曲位移形函數為ψ(y)。則混凝土板任意一點的縱向位移可表示為：

根據Sun 等[31]的研究，剪切翹曲形函數采用二次函數形式已經相當精確，因此本文選取以下形式的形函數：

式中：α1、α2、α3為翹曲形函數相對幅值；D為考慮軸力自平衡的軸向均勻位移，為確定上述未知參數，參考文獻[32]中的方法，由最小勢能原理，求得：

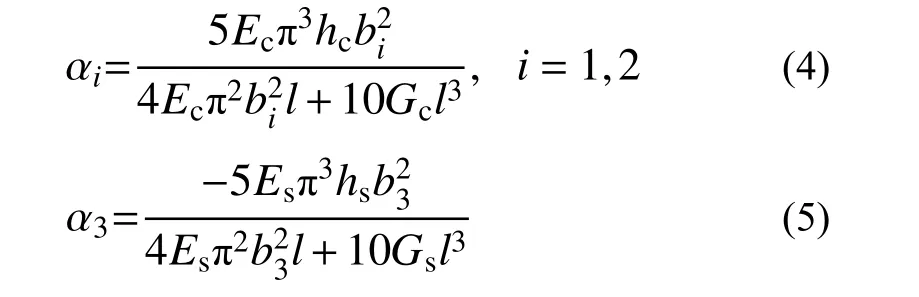
式中，Ec、Gc、Es、Gs、l分別為混凝土彈性模量、混凝土剪切模量、鋼板彈性模量、鋼板剪切模量、組合箱梁跨度。

由軸力自平衡，得到：

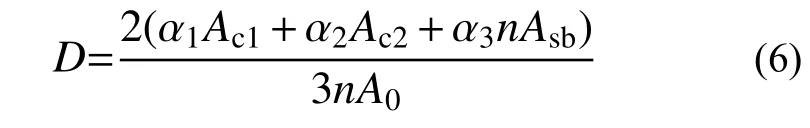
式 中，n=Es/Ec，Ac1=2b1tc，Ac2=2b2tc，Asb=2b3t3，A0為換算截面面積之和。

3.3 勢能表達式

忽略板件的面外剪應變，求得箱梁各點的應變為(為縮短篇幅，后文中所有導數符號均表示對x求導，所有以x為自變量的函數均寫成簡化形式，例如f′表示df(x)/dx)：

根據虛功原理，組合箱梁的總勢能表達式為：

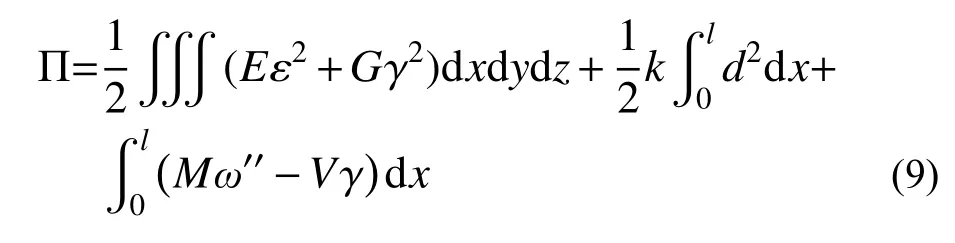
式中，k為單位長度的界面剪切剛度。

將式(7)和式(8)代入式(9)，得到：

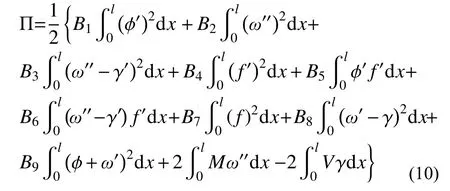
式中，B1～B9由截面特性決定，由于表達式篇幅較長，此處不展開。

3.4 平衡微分方程及求解

根據最小勢能原理，在一切“可取位移”中，彈性體的真實位移應使其總能量取最小值，則對總勢能求變分，有：

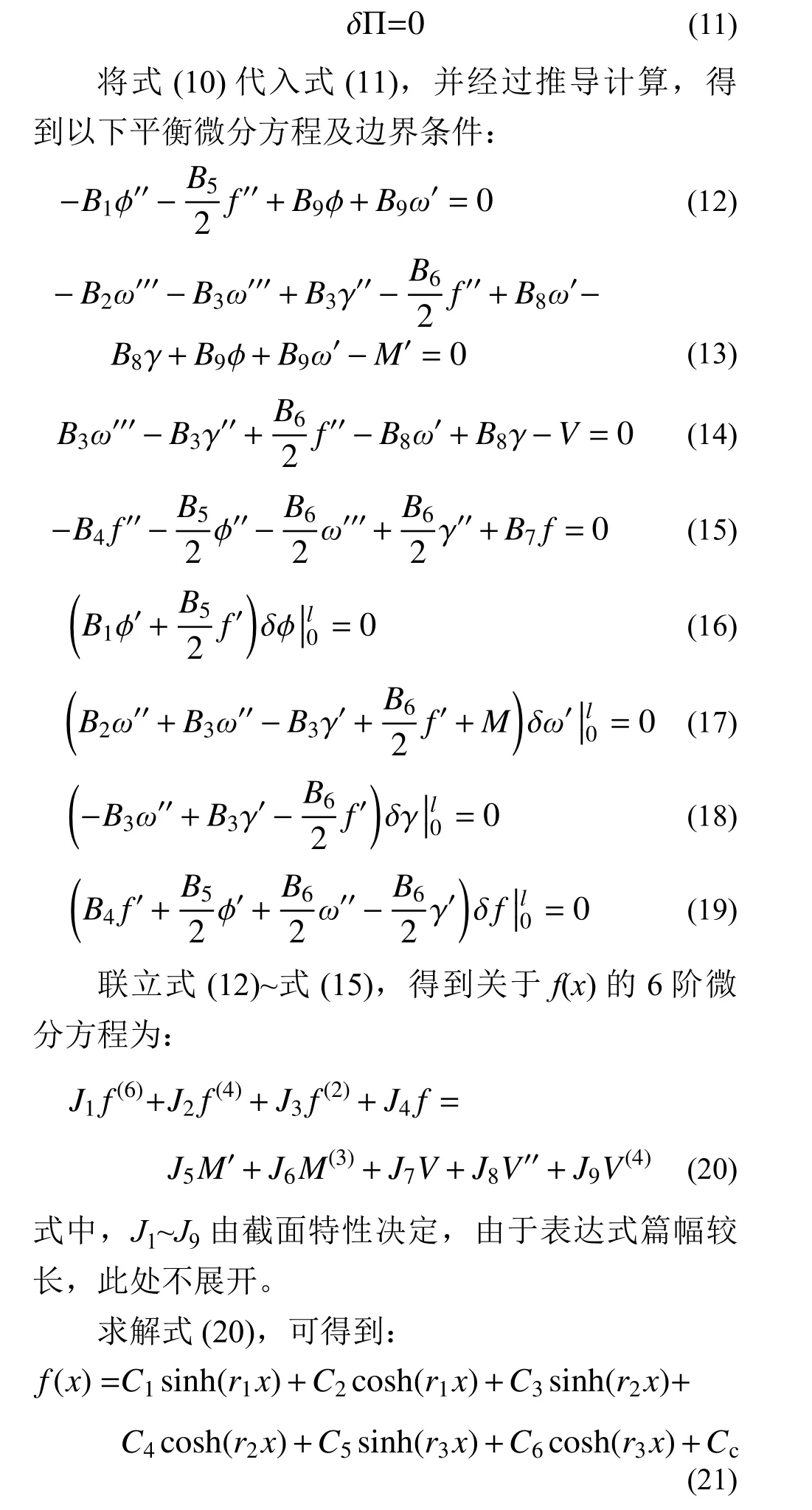
式中：C1～C6為待定系數，需要由位移、變形等邊界條件確定；Cc是僅與截面形式和荷載條件有關的系數；r1～r3僅與J1～J4相關；上述求解過程較為簡單，此處不贅述。

將式(21)代入式(12)～式(15)，可得：

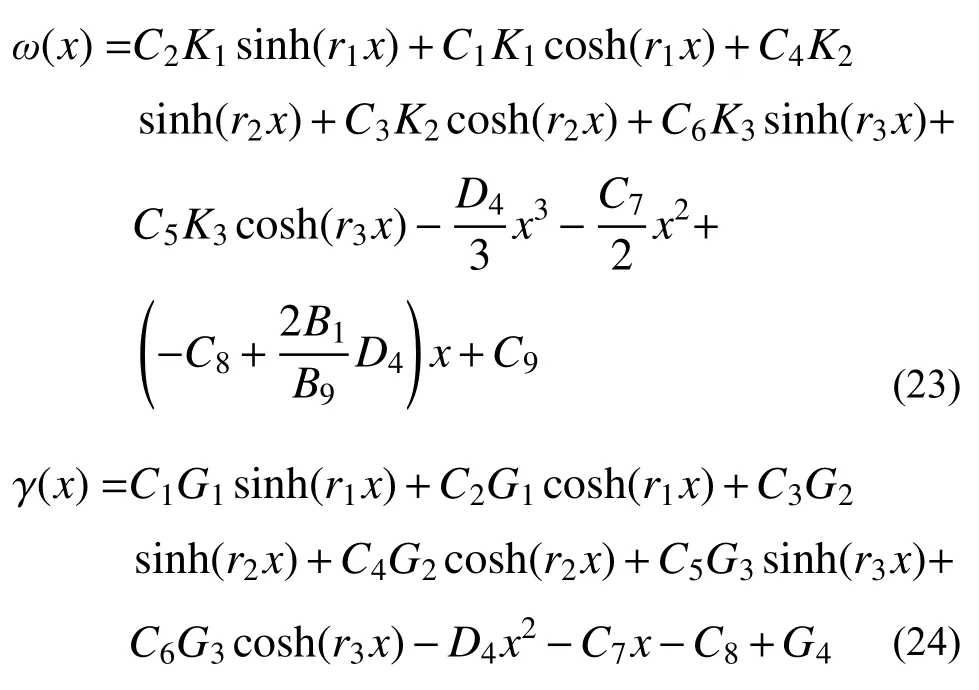
式中：D1～D4、K1～K3、G1～G4是僅與截面形式和荷載條件有關的系數；C7～C9為待定系數，需要由位移、變形等邊界條件確定。

3.5 解析解的驗證

基于本文試驗，考慮組合箱梁的變形，由于試件及邊界均具有對稱性，因此只需考慮0≤x≤l/2 的半跨箱梁。外力V(x)=P/2。

對于跨中單點加載的簡支梁，顯然可得以下邊界條件：

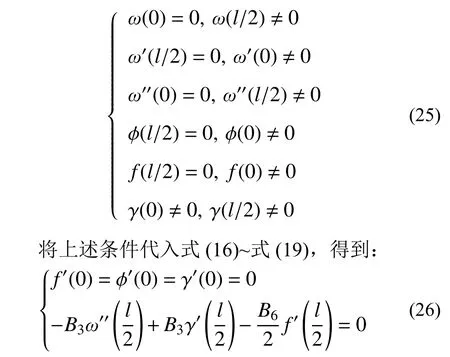
將式(21)～式(24)代入式(25)和式(26)的邊界條件，可求得系數C1～C9的值。

計算總荷載P=1000 kN 時的試件變形，并驗證文獻[11]中不考慮腹板剪切變形的方法。如圖9所示為跨中截面縱向應變沿橫向的分布情況，本文解析解與試驗值基本吻合，而不考慮腹板剪切的解析解明顯低估了縱向應變大小，主要原因是本文試件的跨高比相對較小，腹板剪切變形不可忽略。但試驗值未能完全落在解析解的曲線上，原因主要包括：1)解析解存在較多的假定，實際構件中受力情況復雜，理論推導無法完全準確地描述構件的行為；2)試驗的應變測量本身具有一定誤差，該誤差包括不可避免的系統誤差以及難以預測的偶然誤差；3)為了滿足觀測需求，實際構件在鋼底板做開洞處理，增加了構件受力的復雜性。

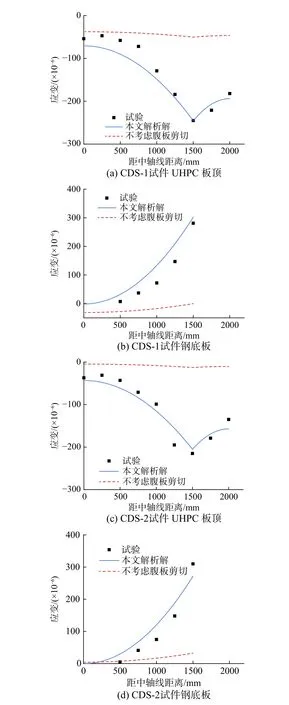
圖9 跨中縱向應變分布的解析解與試驗值對比Fig. 9 Comparison between analytical and experimental longitudinal strain distributions in midspan

圖10 所示為P=1000 kN 時組合箱梁撓度沿縱向的分布情況，可見不考慮腹板剪切的解析解預測效果較差。對于試件CDS-1，實際跨中撓度為0.55 mm，本文解析解撓度為0.50 mm，誤差約為9.1%；對于試件CDS-2，實際跨中撓度為0.48 mm，本文解析解撓度為0.42 mm，誤差約為12.5%。實際試件中鋼底板共有3 處開洞處理，解析解無法考慮該實際情況，因而撓度的計算存在一定低估。

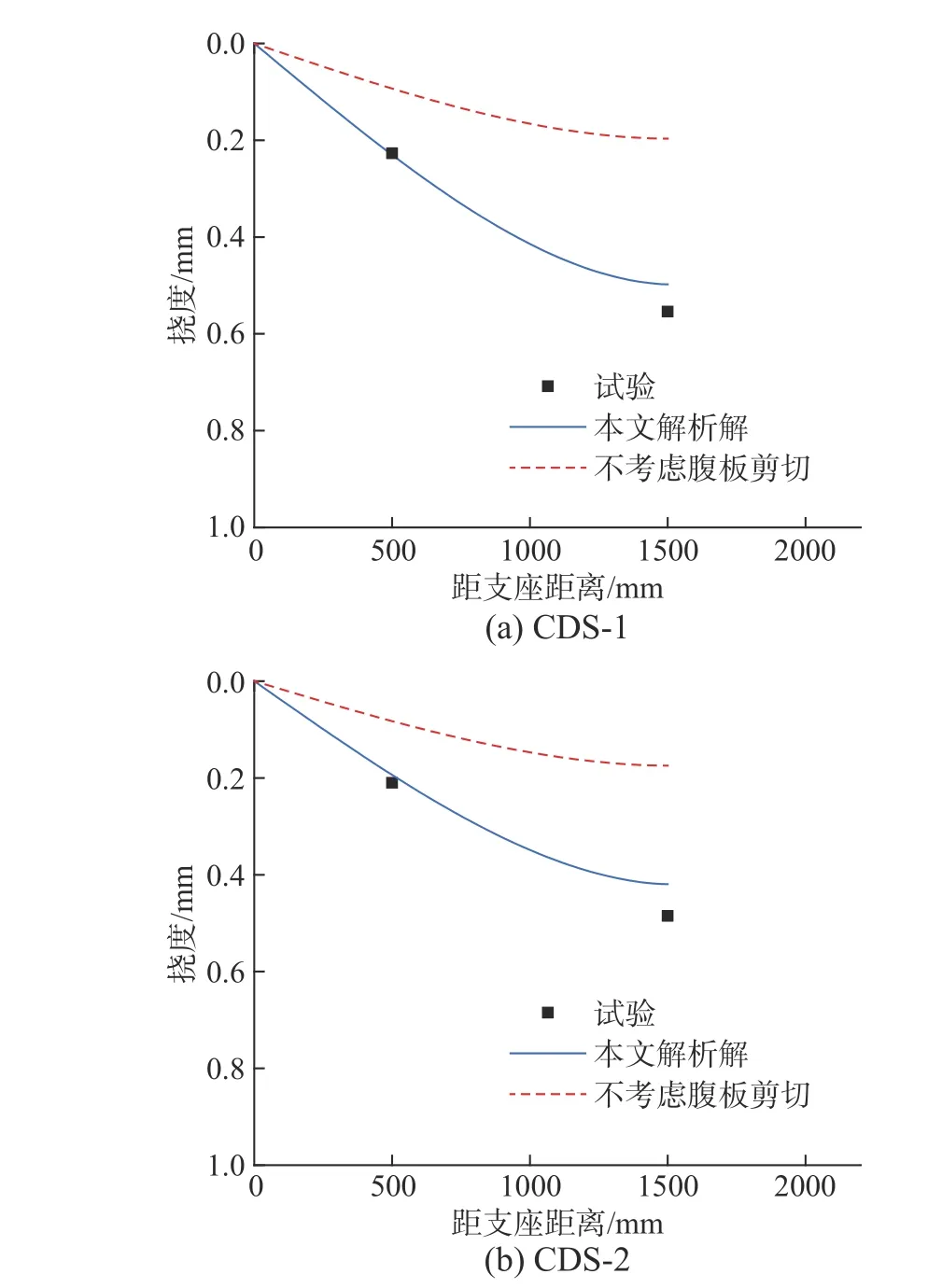
圖10 箱梁撓度的解析解與試驗值對比Fig. 10 Comparison between analytical and experimental deflections of box girder

匯總理論模型結果如表5 所示，可知相同荷載下，UHPC 板厚越大，組合梁跨中撓度越小、UHPC 板和鋼底板應變水平越低。

表5 理論模型主要結果Table 5 Main results of theoretical model

4 結論

本文通過大比例試驗，針對新型鋼-UHPC 組合箱型橋面系開展了研究，并推導考慮剪力滯后、滑移效應以及鋼腹板剪切變形的組合箱梁解析解，得出以下主要結論：

(1) 集中荷載作用下，剪力滯效應較為明顯，UHPC 跨中截面縱向壓應變的最大值與最小值之比約為5～7；

(2) 相同荷載下，隨著UHPC 板厚增加，鋼-UHPC 組合箱梁的剛度提高，UHPC 板和鋼梁應變和應力水平均降低；

(3) 加載點位于鋼腹板正上方的工況下，組合箱梁撓度的橫向差異較小；

(4) 跨高比較小的情況下，鋼腹板剪切變形不可忽略，與僅考慮剪力滯后和滑移效應的模型相比，考慮剪力滯后、滑移效應以及鋼腹板剪切變形的組合箱梁解析解與試驗值吻合更好，誤差相對較小。