基于動力特性的混合結構地震響應復模態疊加法

孫攀旭，楊 紅,2，劉慶林3(. 重慶大學土木工程學院，重慶；重慶大學山地城鎮建設與新技術教育部重點實驗室，重慶；深圳信息職業技術學院交通與環境學院，深圳 5872)

由不同阻尼特性材料組成的工程結構稱為混合結構，目前已經廣泛應用到機械工程、航空航天工程、土木工程等領域。混合結構是非比例阻尼體系，對應的阻尼矩陣不再滿足經典阻尼條件，如何求解混合結構的動力響應是抗震分析中亟待解決的問題。解決該問題的常見方法是，采用應變能法[1 ? 4]、近似解耦法[5 ? 6]、復頻率法[7 ? 8]、Rayleigh 阻尼法[9 ? 11]等計算出等效阻尼比，進而基于傳統的實模態疊加法計算結構動力響應。上述方法的思路是將混合結構簡化為等效的單一材料比例阻尼體系，這容易導致一定的誤差，計算精度難以保證。Foss[12]將運動方程擴展為狀態方程組，進而提出了狀態空間法。依據狀態空間法，可實現混合結構的復模態疊加法，在復數域中求得運動方程的精確解[13 ? 16]。復模態疊加法計算結果的正確性依賴于阻尼矩陣的合理構造，但在結構地震反應分析中，合理地構造出能正確反映結構真實情況的阻尼矩陣是十分困難的[17]。

Rayleigh 阻尼模型假定結構的阻尼矩陣是質量矩陣和剛度矩陣的線性組合[18]，由于數學處理上的簡易性，使其得到了廣泛的應用。Clough 等[19]將子結構的阻尼矩陣假定為Rayleigh 阻尼矩陣，進而組裝得到混合結構的分塊Rayleigh 阻尼矩陣。保證分塊Rayleigh 阻尼模型合理性的關鍵在于如何確定阻尼系數。阻尼系數的計算方法不合理將帶來較大誤差[20 ? 22]。針對如何確定Rayleigh阻尼系數的問題，國內外學者進行了系統研究，Idriss 等[23]僅采用結構的基本頻率確定阻尼系數，Yoshida 等[24]提出了在主要頻率范圍內計算阻尼系數的方法，Hudson 等[25]依據結構的基本頻率和地震波的卓越頻率確定阻尼系數，鄒德高等[26]、李哲等[27]在考慮結構基本頻率和地震波卓越頻率的基礎上，進一步修正了阻尼系數的計算方法，許紫剛等[28]提出基于基本頻率、地震波卓越頻率與形心頻率的平均值確定阻尼系數。為考慮整個振動頻率范圍內阻尼系數的影響，王田友等[29]依據結構的基本頻率和輸入振動的頻率范圍確定兩個振型，并用于計算阻尼系數，潘旦光等[30 ? 32]以結構位移反應峰值的誤差為目標函數，采用最小二乘法確定阻尼系數。

上述方法依據結構體系的振動特性和/或外激勵的頻譜特性確定阻尼系數，本文在上述研究的基礎上，提出了基于結構動力響應特性確定阻尼系數的新思路。Rayleigh 阻尼系數一般通過選擇兩個重要振型的自振頻率和振型阻尼比進行確定，為保持這一工程常用方法的簡便性，同時解決振型選擇方式不唯一導致地震響應計算結果存在不確定性的問題，本文提出了一種基于動力特性確定Rayleigh 阻尼系數的計算方法，即在求解瞬態反應時，根據結構的前兩階振型確定阻尼系數；求解穩態反應時，根據結構的基本振型和外激勵頻率確定阻尼系數，可有效避免傳統方法計算阻尼系數時振型選擇的不唯一性，從而構建出對應的分塊Rayleigh 阻尼矩陣，實現了混合結構的復模態疊加法。事實上，非比例阻尼模型計算過程需涉及復振型，這樣才能更符合工程問題的本質特性[33]，相比基于等效阻尼比的實模態疊加法，本文提出的基于動力特性的混合結構地震響應復模態疊加法可考慮工程結構中不同阻尼特性材料導致的非比例阻尼特性。

1 基于動力特性的阻尼矩陣構建

1.1 黏性阻尼模型的復模態疊加法

基于黏性阻尼模型的時域運動方程為：

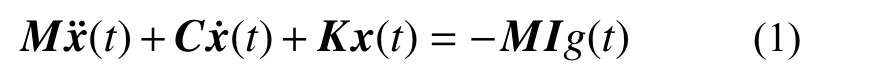
式中：M為質量矩陣；K為剛度矩陣；I為與地震動輸入有關的向量(N×1 )，與g(t)方向相同的位移自由度元素為1。

由M和K可計算得到結構的無阻尼自振頻率，進一步依據分塊Rayleigh 阻尼模型[19]，阻尼矩陣可表示為：

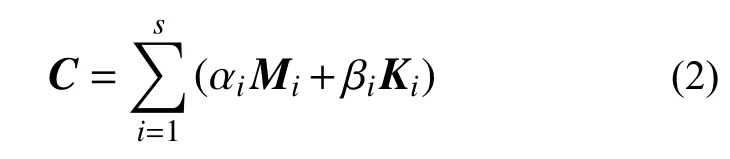
1.2 基于動力特性的阻尼矩陣構造

混合結構復模態疊加法的正確性依賴于合理的阻尼矩陣，目前常用的阻尼矩陣構造方法為分塊Rayleigh 阻尼模型。Rayleigh 阻尼模型的實質是選擇兩個重要的振型，以便使計算的結構動力響應逼近結構的實際響應。結構承受地面運動激勵時需要考慮瞬態反應和穩態反應[19]，因此本文依據瞬態反應和穩態反應的特性分別確定對結構動力響應貢獻最大的兩個振型，進而構建出阻尼矩陣。

考慮到地震波可以分解為一系列簡諧波，因此首先分析諧波作用下基于黏性阻尼模型的時域運動方程，對應的方程形式為：

隨著振型階數的增加，ωj逐漸增大，振幅的幅值H逐漸減小，qpj(t)逐漸減小，同時振型參與系數 γj也逐漸減小；當阻尼比 ξj較小， 2ξjβj的大小可忽略不計， βj接近1 時，振幅的幅值趨近于無窮大，此時結構發生共振現象。因此，在結構的穩態反應xp(t)中，最重要的兩階振型分別為第一階振型以及與外激勵頻率接近的振型。

綜上，本文提出了基于結構線彈性響應分離的經典思路構造分塊Rayleigh 阻尼矩陣的新方法，即針對瞬態反應部分，選擇與第一階振型和第二階振型對應的自振頻率、振型阻尼比構造分塊Rayleigh 阻尼矩陣；針對穩態反應部分，選擇第一階振型以及與外激勵頻率接近振型所對應的自振頻率、振型阻尼比構造分塊Rayleigh 阻尼矩陣。

2 基于地震波卓越頻率的混合結構復模態疊加法

2.1 基于地震波卓越頻率的阻尼矩陣

地震波作用下基于分塊Rayleigh 阻尼矩陣模型的齊次運動方程為：

依據1.2 節分析，求解齊次方程通解時，選取第一階振型和第二階振型對應的自振頻率和振型阻尼比，可計算出阻尼系數為：

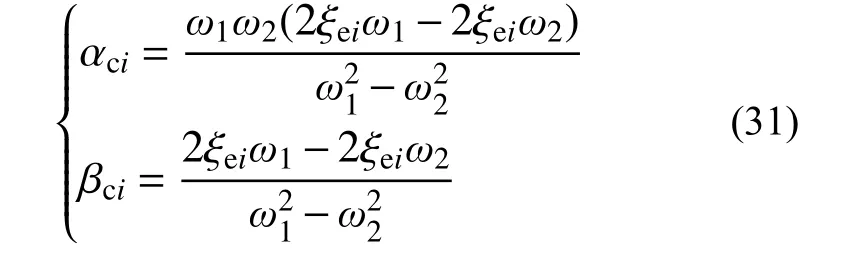
式中：ω1為第一階振型的自振頻率；ω2為第二階振型的自振頻率； ξei為第i種材料對應子結構的材料阻尼系數產生的振型阻尼比[9, 34 ? 35]。

地震波作用下基于分塊Rayleigh 阻尼矩陣的非齊次運動方程為：

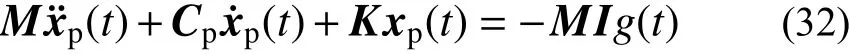
穩態反應對應的阻尼矩陣可表示為：

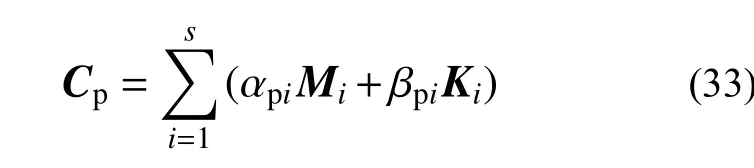
依據1.2 節分析，求解非齊次方程特解時，選擇第一階振型、與外激勵頻率接近振型對應的自振頻率和振型阻尼比。目前確定阻尼系數的計算方法較多[23 ? 32]，本文對比了利用結構基頻確定阻尼系數的方法、利用最小二乘法確定阻尼系數的方法、利用結構基頻和地震波卓越頻率確定阻尼系數的方法。選擇不同的方法并不影響以下理論推導過程，為了更清楚地展示本文方法的核心思路、保持計算的簡便性，并考慮同時利用結構振動特性和地震動特性，本文首先選擇依據結構的第一階振型自振頻率、地震波卓越頻率確定阻尼系數，進一步可得：

綜上，由式(35)可確定阻尼系數，進而得到了基于地震波卓越頻率的分塊Rayleigh 阻尼矩陣。

2.2 基于地震波卓越頻率的復模態疊加法

采用數值積分方法進行計算時，按照時間步長 ?t對輸入地震動加速度記錄進行離散，任意時刻可表示為tk=k?t(k=0,1,2,···) ，利用tk時刻結構的動力響應，計算tk+1時刻的響應。由式(16)可知，求解混合結構的加速度響應需要計算方程式(14)中單自由度結構的加加速度(即qj(t)的三階微分)，因此傳統的時域逐步積分計算方法將不再適用，本文采用瞬態反應與穩態反應分離的時域數值方法計算結構的動力響應。

重復式(36)～式(45)，可實現基于地震波卓越頻率的混合結構復模態疊加法。

3 基于地震波的諧波頻率的混合結構復模態疊加法

3.1 基于諧波頻率的阻尼矩陣

對于頻帶較寬的地震波，卓越頻率不能有效地表現地震波的主要頻譜特性，為此本文對基于地震波卓越頻率的阻尼矩陣進行改進，將輸入地震波加速度采用三角級數展開，得：

綜上，由式(51)可確定阻尼系數，進而得到基于諧波頻率的分塊Rayleigh 阻尼矩陣。

3.2 基于諧波頻率的復模態疊加法

為實現基于諧波頻率的復模態疊加法，首先計算齊次運動方程對應的通解xc(t)，與基于地震波卓越頻率的復模態疊加法相同，解耦后的齊次方程為式(36)，求解可得：

依據復特征向量的正交性，可由xc(t0) 和x˙c(t0)得到qcj(t0) 和q˙cj(t0)，完成初值的確定，進而實現基于諧波頻率的混合結構復模態疊加法。

4 試驗校核與計算分析

圖1 試件動力響應的試驗系統Fig. 1 Test system of specimens’ dynamic responses

將由不同阻尼特性材料組成的懸臂板試件作為試驗對象采用圖1 所示的試驗測試系統，通過振動臺控制系統對試件的基底施加隨機激勵，同時采用多普勒振動測試系統測量試件的動力響應。振動測試系統可直接采集試件的速度響應，需根據采集頻率進行相應的積分或微分處理才能得到構件的位移或加速度響應，為避免后期的數據再處理導致的誤差，本文僅分析了試件的速度響應，以驗證本文方法的正確性。

懸臂板試件的具體尺寸如圖2 所示，拾振點的位置如圖3 所示，考慮到4 個拾振點的位置是對稱分布的，本文僅選取拾振點A和拾振點B的動力響應進行分析、對比。試驗選取尺寸和材料相同的2 個試件(CP-1 和CP-2)進行測試，試件的材料參數如表1 所示，子結構的振型阻尼比為對應材料損耗因子的1/2[38?40]，基層結構的振型阻尼比為0.0015，阻尼層結構的振型阻尼比為0.295。采用數值模擬，由試件的整體質量矩陣和整體剛度矩陣通過模態分析可得到試件的前5 階振型的無阻尼自振頻率為15.26 Hz、35.58 Hz、90.13 Hz、118.54 Hz 和132.41 Hz。

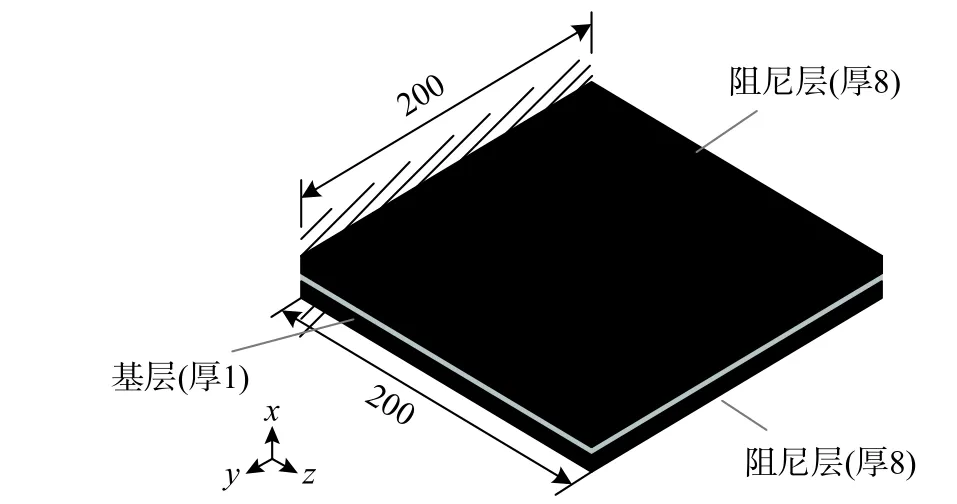
圖2 試件的尺寸 /mm Fig. 2 Size of specimen

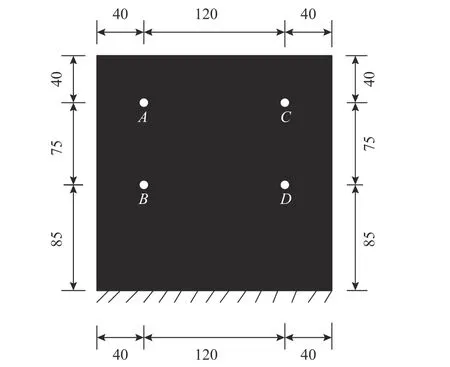
圖3 拾振點的位置 /mm Fig. 3 Locations of vibration receiving points

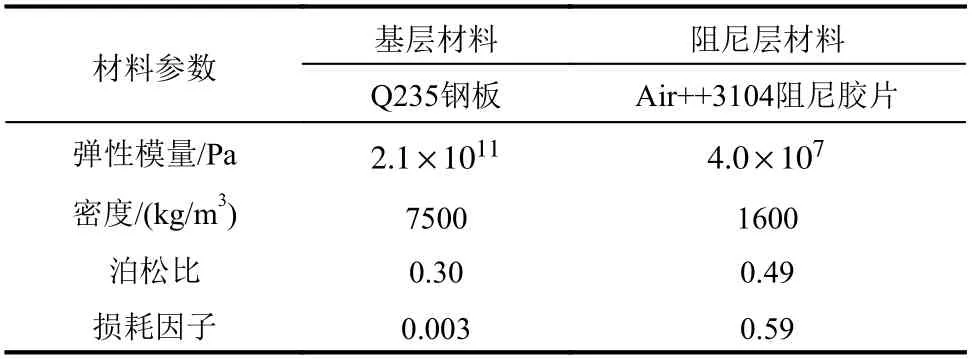
表1 試件的材料參數Table 1 Material parameters of specimen

4.1 試件CP-1 的試驗結果和計算結果對比

利用振動臺控制系統，對試件CP-1 施加隨機激勵，其振動頻率的范圍為100 Hz～150 Hz。由信號采集系統可得到隨機激勵的加速度時程(見圖4(a))和對應的傅里葉譜(見圖4(b))。分別采用基于第一階振型和第二階振型的復模態疊加法(CRS)、本文提出的基于地震波卓越頻率的復模態疊加法(CRZ)和基于地震波的諧波頻率的復模態疊加法(CRX)計算試件CP-1 在隨機激勵作用下的速度時程，并將其分別與多普勒振動測試系統測量的試件速度響應時程(CP-1-Test)進行對比，結果如圖5 所示。如表2 所示，對比拾振點A的速度峰值IA，CRS的相對誤差 δA為39.33%，CRZ 的相對誤差 δA為10.49%，CRX 的相對誤差 δA為8.16%；對比拾振點B的速度峰值IB，CRS 的相對誤差 δB為32.19%，CRZ 的相對誤差 δB為15.78%，CRX 的相對誤差δB為11.90%。結果表明，相比CRS，考慮了地震動頻譜特征影響的CRZ 和CRX 的計算精度更高；對于窄頻帶的外激勵，相比CRZ，CRX 的計算精度并沒有明顯提高，但CRX 的計算量較大。因此，對于窄頻帶的外激勵，應優先選用CRZ。

4.2 試件CP-2 的試驗結果和計算結果對比

利用振動臺控制系統對試件CP-2 施加頻帶較寬的隨機激勵，其振動頻率的范圍為40 Hz～150 Hz。由信號采集系統可得到隨機激勵的加速度時程(見圖6(a))和對應的傅里葉譜(見圖6(b))。分別采用CRS、CRZ 和CRX 計算試件CP-2 在隨機激勵作用下的速度時程，并分別與多普勒振動測試系統得到的速度時程(CP-2-Test)進行對比，結果如圖7所示。如表3 所示，對比拾振點A的速度峰值IA，CRS 的相對誤差 δA為23.45%，CRZ 的相對誤差 δA為13.11%，CRX 的相對誤差 δA為7.92%；對比拾振點B的速度峰值IB，CRS 的相對誤差 δB為47.50%，CRZ 的相對誤差 δB為19.28%，CRX 的相對誤差 δB為11.15%。結果表明，與試件CP-1 的分析結果相同，CRZ 和CRX 的計算精度相比CRS 明顯更高。與試件CP-1 不同的是，隨著外激勵頻帶增寬，CRX 的計算精度比CRZ 明顯增高。因此，CRZ 計算量更小、適用范圍受限，CRX 的計算精度更高，具有更寬泛的適用范圍，在對計算精度有要求時，建議采用CRX。

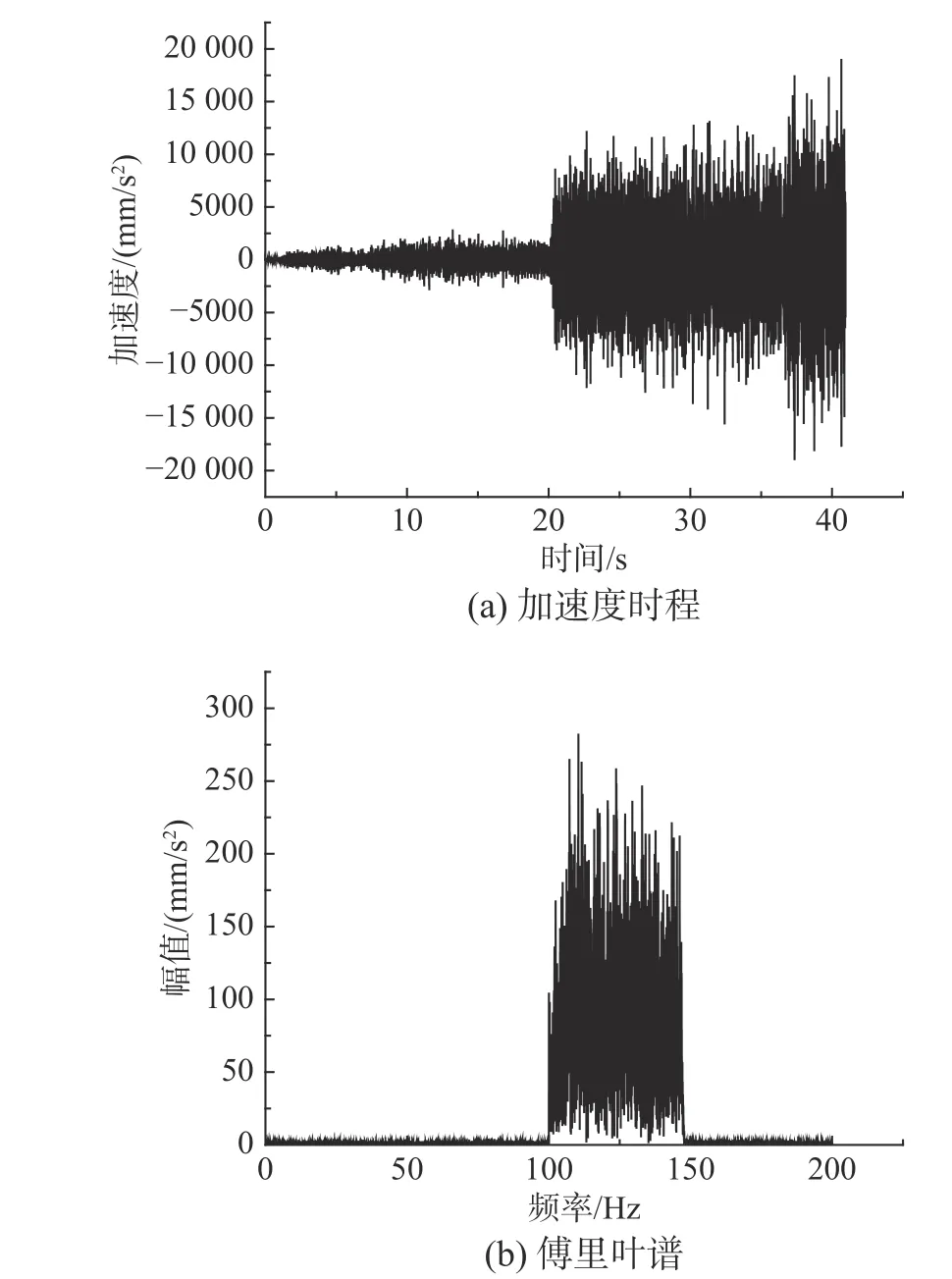
圖4 試件CP-1 的隨機激勵Fig. 4 Random external excitation of specimen CP-1

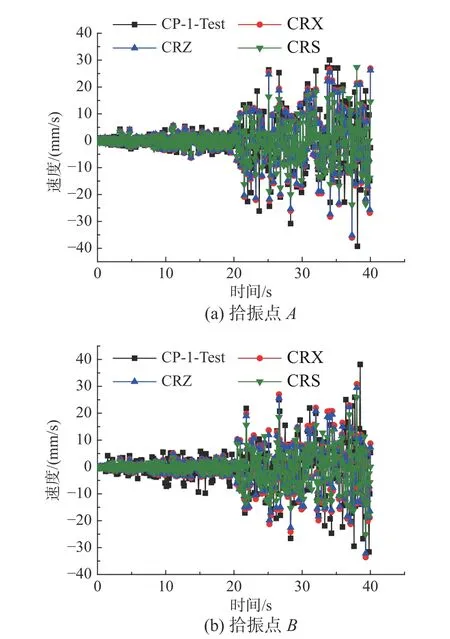
圖5 試件CP-1 的速度響應時程Fig. 5 Velocity time-history responses of specimen CP-1

5 算例分析

如圖8 所示，模型A 和模型B 是由不同阻尼特性材料組成的7 層平面框架，1 層～4 層均為鋼筋混凝土結構、5 層～7 層為鋼結構。框架底層高度皆為6 m、其余各層層高均為3 m，跨度均為6 m，鋼筋混凝土柱、梁的截面尺寸分別為400 mm×500 mm、300 mm×400 mm，鋼柱、梁的截面尺寸分別為HM400 mm×300 mm×10 mm×16 mm、HM300 mm×200 mm×8 mm×12 mm，各 樓 層 集 中 質 量 皆 為2 0000 kg。與模型A 相比，模型B 的唯一區別是增設了X 型阻尼器，材料參數見表4。

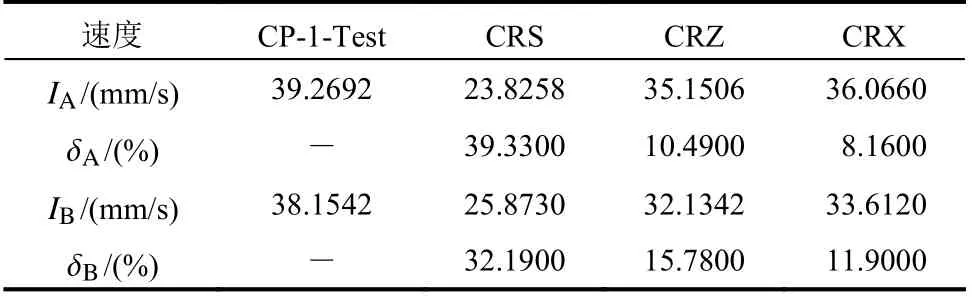
表2 試件CP-1 的動力響應對比Table 2 Comparisons of dynamic responses of specimen CP-1

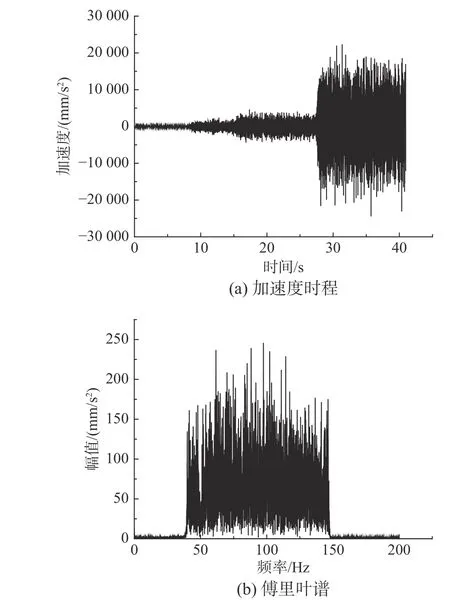
圖6 試件CP-2 的隨機激勵Fig. 6 Random external excitation of specimen CP-2

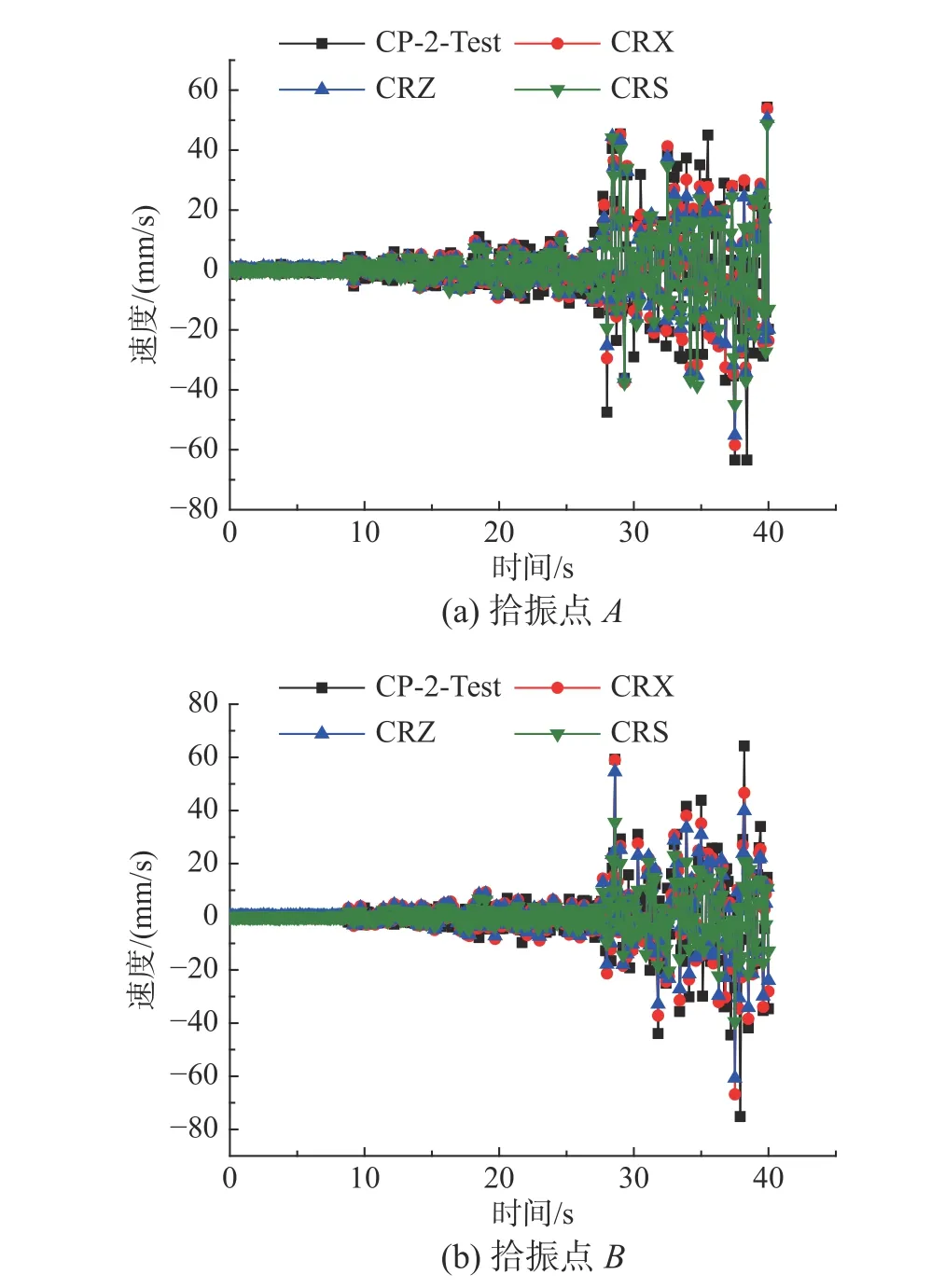
圖7 試件CP-2 的速度響應時程Fig. 7 Velocity time-history responses of specimen CP-2

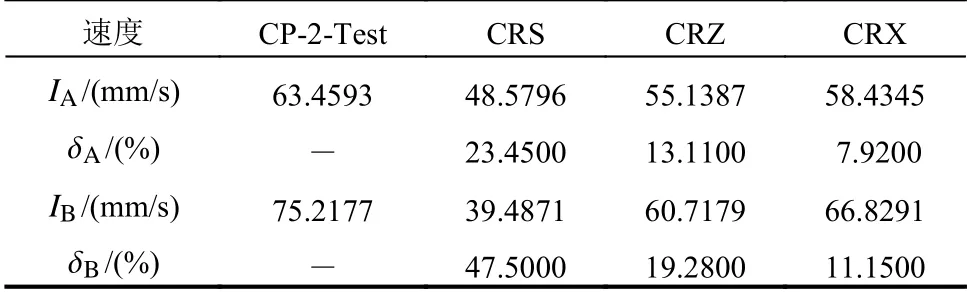
表3 試件CP-2 的動力響應對比Table 3 Comparisons of dynamic responses of specimen CP-2

地震動輸入選取天津地震波和遷安地震波，對應的加速度時程和傅里葉幅值譜分別如圖9 和圖10 所示。其中，天津地震波的頻帶較窄，遷安地震波的頻帶較寬。分別采用基于應變能法的實模態疊加法(RY)[1 ? 4]、CRZ 和CRX 計算模型A、模型B 在地震波作用下結構頂層節點1(位置見圖8)的動力響應，結果如圖11、圖12、圖13 和圖14所示。

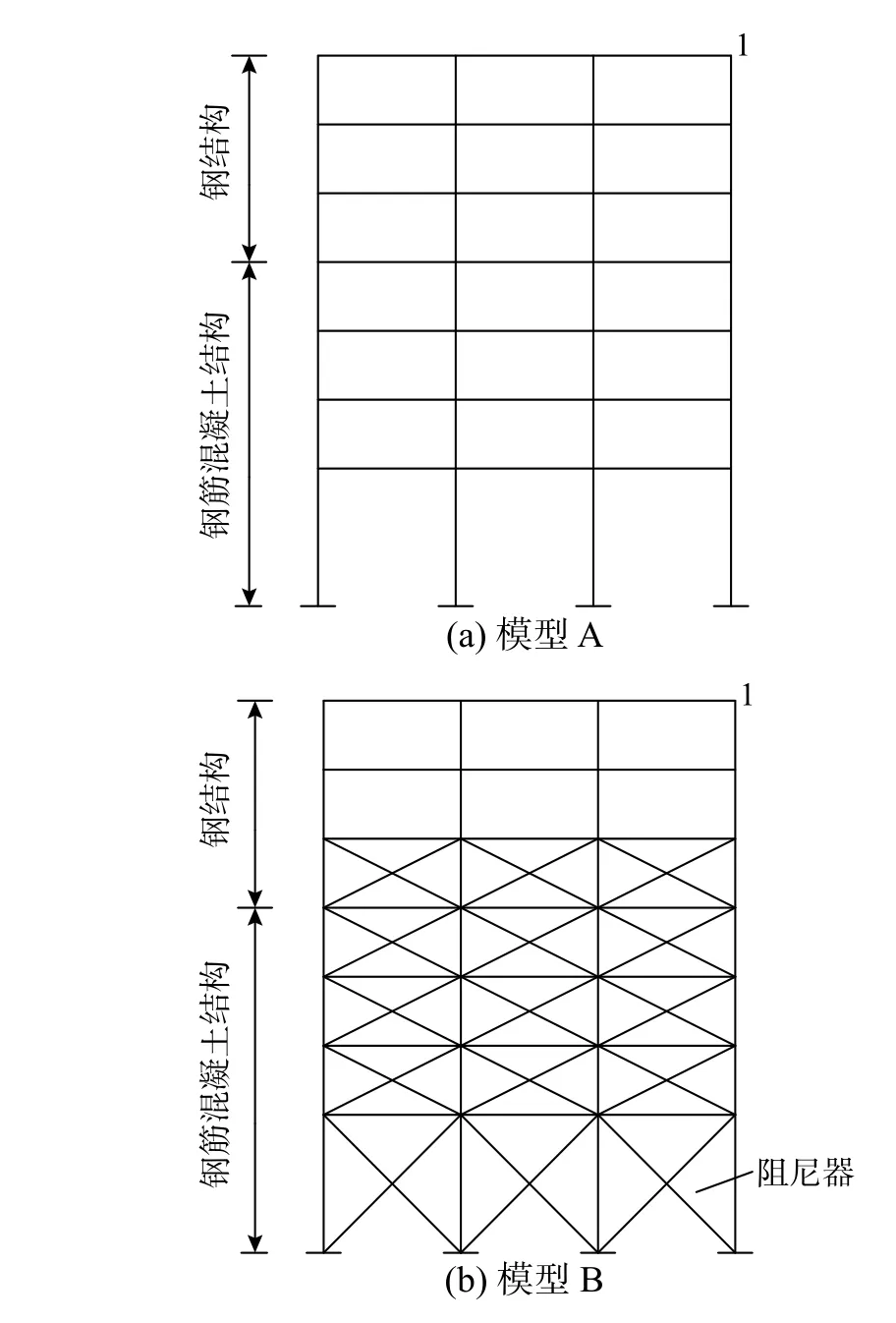
圖8 模型示意圖Fig. 8 Schematics of structural models

表4 不同材料的參數Table 4 Parameters of different materials

對于模型A，天津地震波作用下，RY、CRZ和CRX 計算得到的頂層動力響應時程近似相等(見圖11)。相比RY，CRZ 的位移峰值相對誤差為3.65%，加速度峰值相對誤差為2.47%；CRX的位移峰值相對誤差為0.35%，加速度峰值相對誤差為在0.30%(見表5)。遷安地震波作用下，RY和CRX 計算得到的頂層加速度時程近似相等，但CRZ 計算得到的動力響應時程明顯不同(見圖12)。相比RY，CRZ 的位移峰值相對誤差為19.78%，加速度峰值相對誤差為14.96%；CRX 的位移峰值相對誤差為0.27%，加速度峰值相對誤差為在0.18%(見表5)。因此，對于非比例阻尼特性較小的混合結構，RY 和CRX 的計算結果近似相等，而CRZ 僅適用于計算窄頻帶地震波作用下結構動力響應。

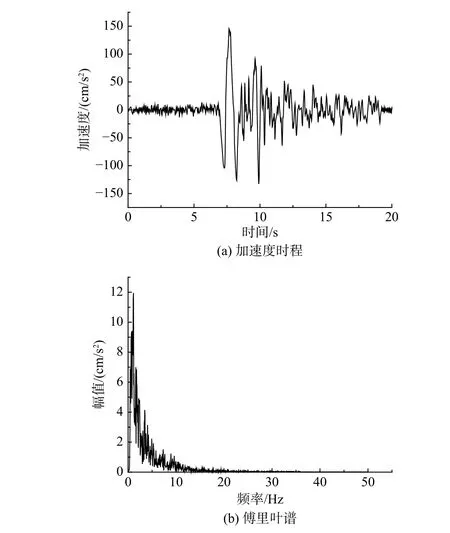
圖9 天津地震波的加速度時程和傅里葉譜Fig. 9 Acceleration time-history and Fourier amplitude spectrum of Tianjin seismic wave

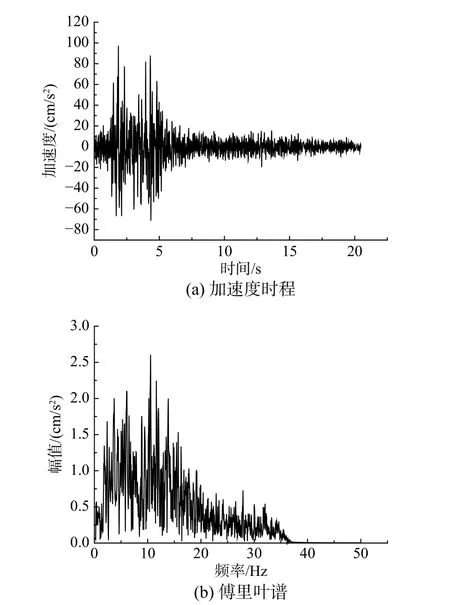
圖10 遷安地震波的加速度時程和傅里葉譜Fig. 10 Acceleration time-history and Fourier amplitude spectrum of Qian'an seismic wave

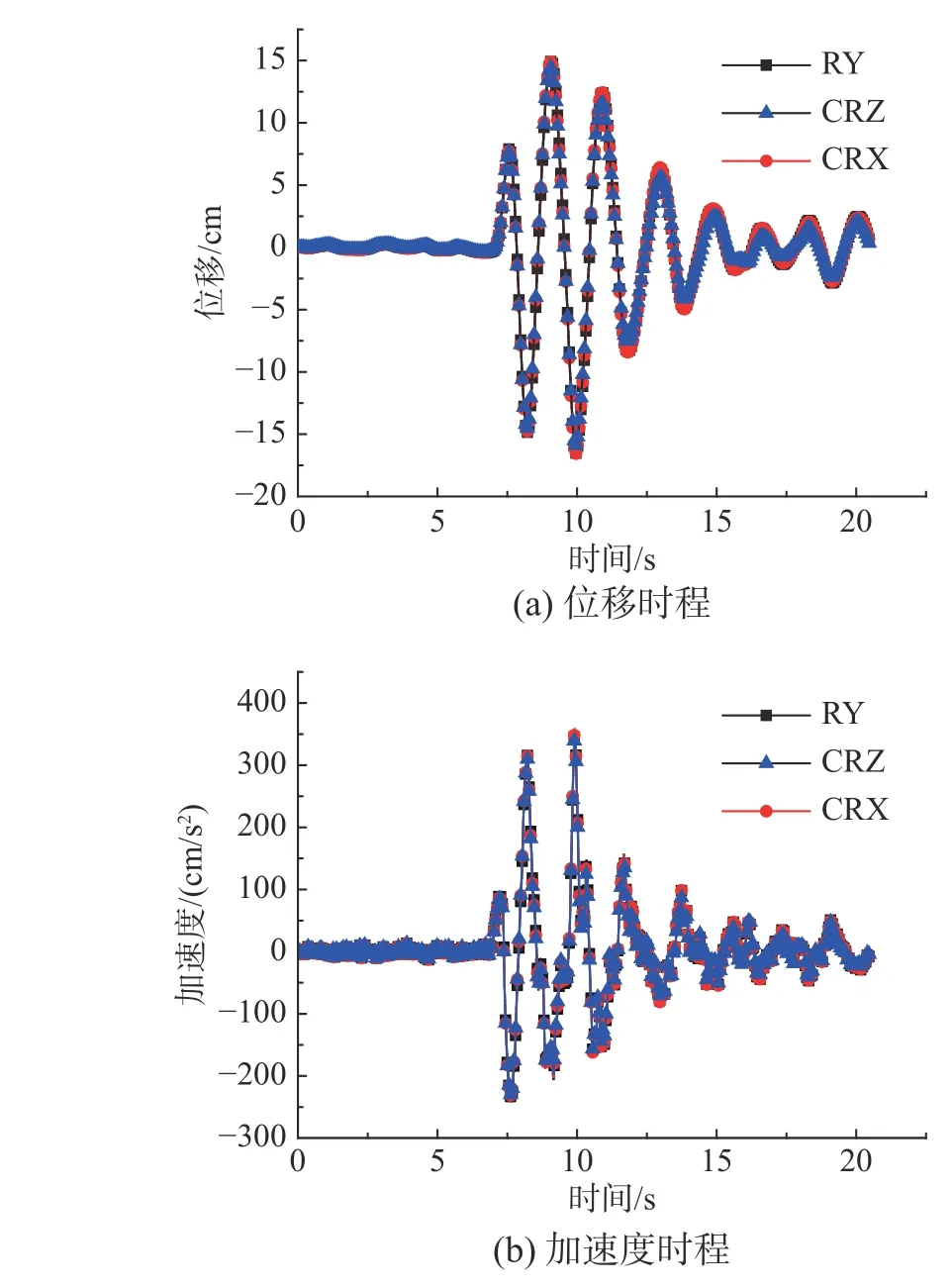
圖11 天津波作用下模型A 的頂層時程響應Fig. 11 Top floor time-history responses of Model A under Tianjin wave

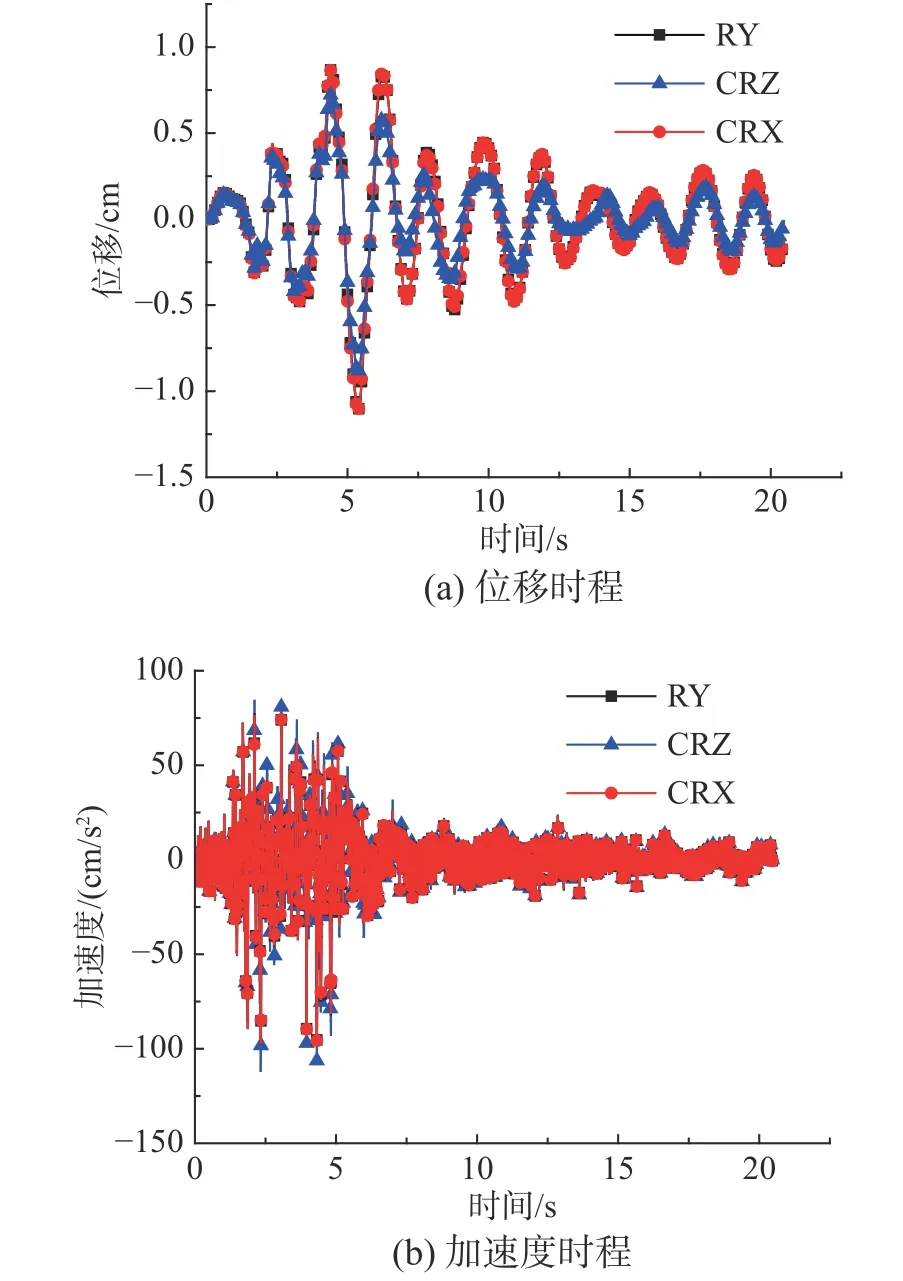
圖12 遷安波作用下模型A 的頂層時程響應Fig. 12 Top floor time-history responses of Model A under Qian'an wave

圖13 天津波作用下模型B 的頂層時程響應Fig. 13 Top floor time-history responses of Model B under Tianjin wave

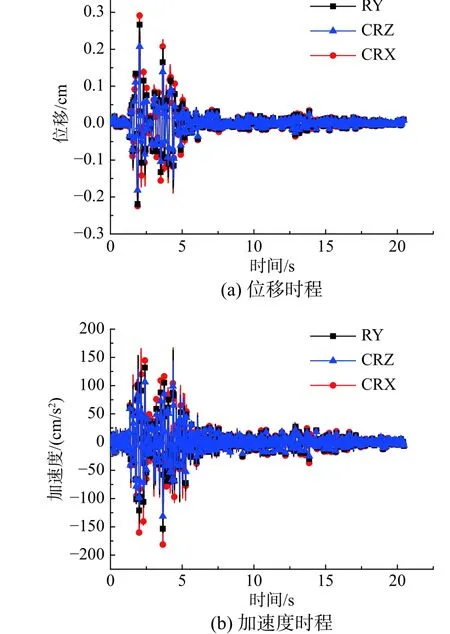
圖14 遷安波作用下模型B 的頂層時程響應Fig. 14 Top floor time-history responses of Model B under Qian'an wave

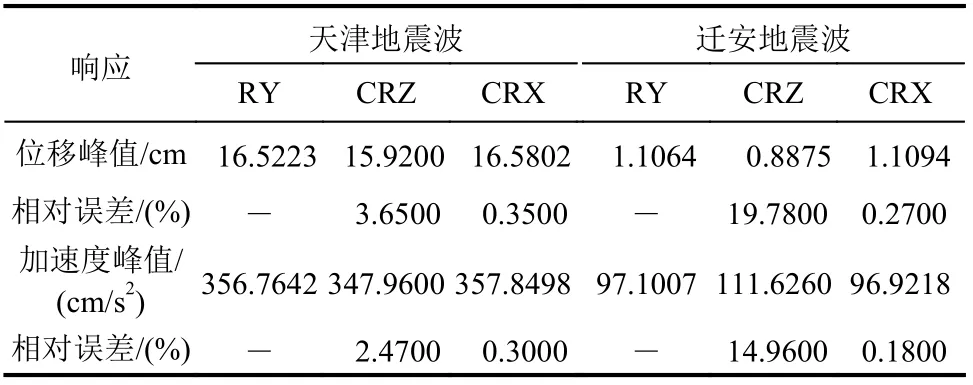
表5 模型A 的頂層響應對比Table 5 Comparisons of top floor responses of Model A

對于模型B，天津地震波作用下，CRZ 和CRX計算得到的頂層動力響應時程近似相等，RY 計算得到的動力響應時程明顯不同(見圖13)。相比RY，CRZ 的位移峰值相對誤差為12.85%，加速度峰值相對誤差為22.11%；CRX 的位移峰值相對誤差為10.19%，加速度峰值相對誤差為在17.16%(見表6)。遷安地震波作用下，RY、CRZ 和CRX計算得到的模型B 頂層加速度時程明顯不同(見圖14)。相比RY，CRZ 的位移峰值相對誤差為22.21%，加速度峰值相對誤差為11.58%；CRX 的位移峰值相對誤差為12.12%，加速度峰值相對誤差為在11.98%(見表6)。因此，對于非比例阻尼特性較大的混合結構，RY 與CRZ、CRX 的計算結果差異較大。與模型A 的規律相同，窄頻帶地震波作用下，CRZ 和CRX 的計算結果近似相等，隨著地震波頻帶的增寬，CRZ 與CRX 的計算結果差異增大。

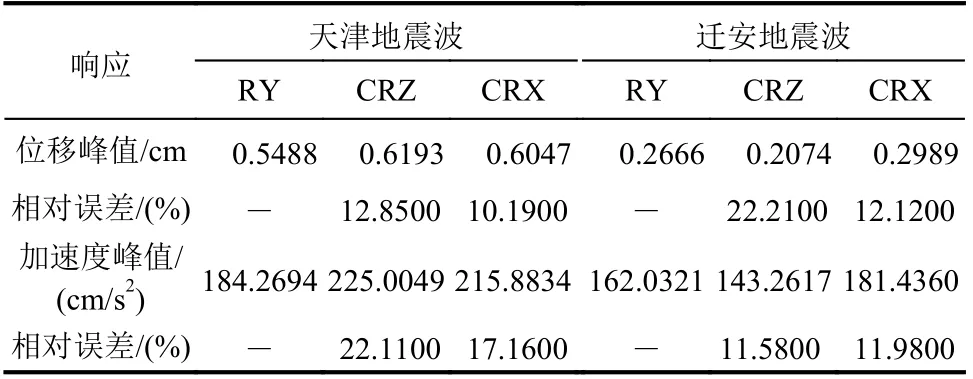
表6 模型B 的頂層響應對比Table 6 Comparisons of top floor responses of Model B

綜上，對于非比例阻尼特性較小的混合結構，RY 與CRZ、CRX 的計算結果近似相等，隨著混合結構非比例阻尼特性增大，RY 與CRZ、CRX 的計算結果差異增大。與試驗結果的規律相同，CRZ 的計算量小，但僅適用于窄頻帶地震波作用下結構動力響應的計算；CRX 的計算精度更高，且適用于寬頻帶地震波作用下結構動力響應的計算，但計算量大。

6 結論

針對基于Rayleigh 阻尼模型的地震反應分析過程中阻尼系數確定方法存在的問題，本文提出了基于動力特性確定Rayleigh 阻尼系數的新方法，經過理論推導和試驗校核得到以下結論：

(1)求解地震波作用下結構的瞬態反應時，依據結構的前兩階振型確定阻尼系數；求解地震波作用下結構的穩態反應時，依據結構的基本振型、與地震波卓越頻率接近的振型確定阻尼系數，得到基于地震波卓越頻率的分塊Rayleigh 阻尼模型。結合輸入地震波加速度時程在時間步長內線性變化的假定，提出了相應的混合結構復模態疊加法。

(2)卓越頻率僅能反映窄頻帶地震波的頻譜特性。對于具有明顯寬帶頻譜特性的地震波，借助快速傅里葉變換，將輸入地震波加速度表示為一系列諧波的疊加組合，得到每一條諧波的頻率。求解地震波作用下結構的穩態反應時，依據結構的基本振型、與諧波頻率接近的振型確定阻尼系數，得到基于諧波頻率的分塊Rayleigh 阻尼模型，建立了對應的混合結構復模態疊加法。

(3)試驗結果和計算對比分析表明，基于動力響應特性確定Rayleigh 阻尼系數的計算方法避免了傳統方法存在的振型選擇不唯一導致的計算結果不確定的問題，且計算結果誤差較小；與基于地震波卓越頻率的復模態疊加法相比，基于諧波頻率的復模態疊加法計算量更大，但計算精度更高、適用范圍更廣。