適用于黏土的分數階應力誘導剪脹方程
李海潮,馬 博,張 升,2,盛岱超
(1. 中南大學土木工程學院,湖南,長沙 410075;2. 高速鐵路建造技術國家工程實驗室,湖南,長沙 410075;3. 悉尼科技大學土木與環境工程學院,澳大利亞,悉尼 NSW 2007)
不同于正常固結重塑土,超固結重塑土應力-應變曲線具有應變硬化和軟化特征,并且伴隨著剪縮和剪脹現象的發生。修正劍橋(modified Camclay, MCC)模型[1]在描述其力學特性時存在明顯不足,具體表現在以下幾個方面:
首先,MCC 模型的剪脹方程假定土體的剪脹因子僅與當前剪切應力比有關,無法考慮溫度和超固結比等外部加載因素對土體剪脹特性的影響[2 ? 5]。Gao 等[6]在其所建立邊界面模型中深入的探究了黏土的應力歷史對其剪脹特性和應力-應變特性的影響。值得注意的是,即使對于正常固結重塑土,MCC 模型的剪脹方程在描述其剪脹特性時依然存在不足。Wang 和Yin[7]針對自然軟土的試驗結果表明,在材料發生剪縮破壞的過程中,MCC 模型預測的剪縮量要明顯小于試驗值。杜修力等[8]基于統一非線性強度理論建立了適用于正常固結重塑土的剪脹方程。殷杰[9]通過引入結構屈服應力參數建立了適用于結構性軟黏土的修正劍橋模型。
其次,MCC 模型采用相關聯的流動法則,并且基于非線性能量耗散方程假定土體具有橢圓形屈服面。然而試驗結果表明,巖土材料的屈服面具有更為復雜的幾何形狀[2, 10]。Lagioia 等[11]討論了屈服面幾何形狀對模型計算結果的影響;Collins和Kelly[12]則基于現代熱力學理論給出了適用于巖土材料的雙參數屈服函數。此外,剪切過程中巖土材料塑性流動方向并不始終垂直于其物理屈服面[13 ? 14]。Sun 等[15 ? 18]指出可以對屈服函數進行分數階微分得到分數階塑性流動法則,進而在不引入塑性勢函數的情況下統一的描述相關聯和非相關聯的塑性流動法則。在此基礎上,孫逸飛和沈楊[19]建立了適用于粗粒料的靜動力邊界面模型,成功地模擬了粗粒料在靜動力加載條件下的應力-應變行為和循環荷載下的長期變形。Lu 等[20]則基于該方法在 β應力空間建立了適用于正常固結重塑土的分數階修正劍橋模型。
MCC 模型在描述黏土在超固結狀態時的應力-應變響應時同樣存在明顯不足,模型計算得到的剪切強度明顯偏大,且應力-應變曲線為一條不光滑的曲線[21]。為了克服該不足,Dafalias 等[22 ? 23]和Hashiguchi 等[24 ? 26]分別提出了邊界面和下加載面的力學概念。其中,下加載面模型假定在任意加載時刻,材料當前的應力點始終位于下加載面上并發生彈塑性體積變形[27?31];邊界面模型則假定當前應力點位于邊界面內,并且采用某種映射準則計算得到其塑性流動方向和塑性模量[32 ? 36]。
本文首先將Caputo 微分方法應用于MCC 模型的屈服函數,從而得到一個新的分數階剪脹方程用于考慮超固結比對黏土剪脹特性的影響。在此基礎上可以建立適用于黏土的分數階下加載面模型,該模型所采用的分數階塑性流動法則能夠統一的描述相關聯和非相關聯的流動法則。相比較MCC 模型,本文模型僅額外地引入了一個與土體剪脹特性相關的模型參數,同時能夠對超固結黏土的應變軟化和剪脹特性進行合理的描述。
1 應力誘導分數階剪脹方程

1.1 分數階微分定義

孫逸飛和沈楊[19]指出分數階微分具有長程記憶性,適用于描述路徑和記憶依賴性行為。后文將根據分數階微分推導出一個新的應力誘導剪脹方程,并由此建立一個適用于超固結重塑土的分數階下加載面模型。
1.2 分數階塑性流動法則


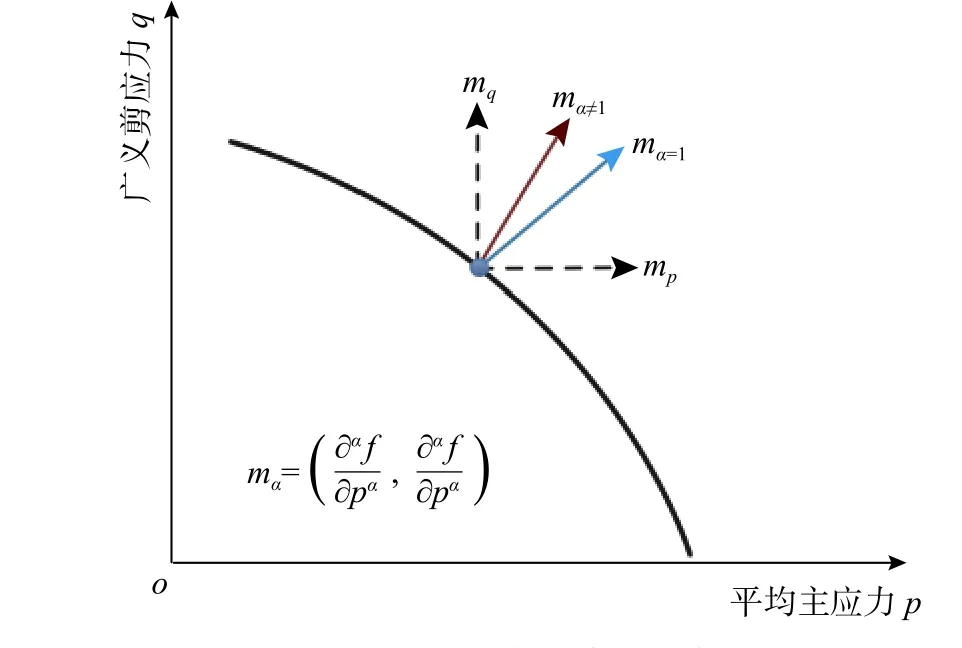
圖1 分數階流動法則示意圖Fig. 1 Schematic plot of fractional flow rule
1.3 正常固結屈服面和相似因子
為了表述超固結重塑土的應變軟化和剪脹特性,本文引入了下加載面的力學概念。如圖2 所示,表征超固結狀態的當前應力點A(p,q)位于下加載面上,而參考應力點B(pˉ,qˉ)則位于正常固結屈服面上。為了動態地描述在p?q平面中下加載面和正常固結屈服面兩者之間相對位置的演變關系,基于徑向映射法則定義了相似因子R:
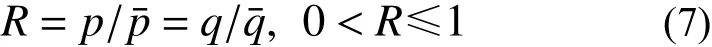
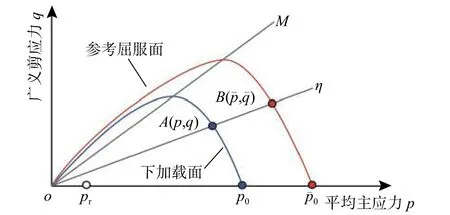
圖2 下加載面示意圖Fig. 2 Schematic plot of sub-loading surface
R與超固結比OCR具有相似的物理意義,在單調加載過程中,隨著土體超固結特性的減弱,R的值逐漸增大,當R=1 時,下加載面與正常固結屈服面最終重合,此時土體處于正常固結狀態。

1.4 分數階剪脹方程

MCC 剪脹方程無法反映溫度和超固結性等外部加載因素對土體剪脹特性的影響,同時對于超固結重塑土,該剪脹方程預測的剪脹量要明顯大于實測值。為此,聯合式(5)、式(9),本文基于Caputo 分數階微分給出了一個新的剪脹方程:


圖3 給出了剪脹因子d隨剪應力比 η和相似因子R的變化規律。可以看出,在相同的應力水平下,d隨著R的增大而逐漸增大,即黏土的剪脹量會隨著超固結性的破壞而逐漸增大,與試驗結果保持一致。
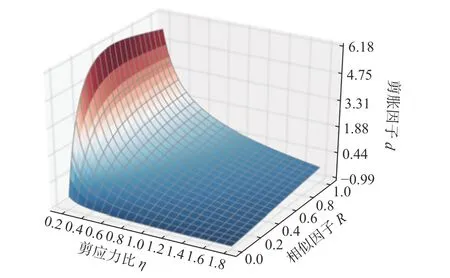
圖3 剪脹因子d 隨剪應力比 η和相似因子R 變化規律Fig. 3 Evolution of dilatancy ratio d with shear stress ratio η and similarity ratio R
2 分數階下加載面模型
基于本文提出的應力誘導分數階剪脹方程,通過給定一個合理的下加載面硬化法則,可以直接建立適用于黏土的分數階下加載面模型。
2.1 下加載面和硬化法則
根據Hashiguchi 等[24 ? 26]的研究成果,本文假定下加載面與正常固結屈服面具有相似的幾何形狀,則下加載面屈服函數f可以表示為:


2.2 模型實現


2.3 參數試驗
這里主要探究參數m的取值對模型計算結果的影響。首先將數值試樣各向同性固結至800 kPa,然后卸載至100 kPa,從而形成OCR=8 的超固結試樣。在此基礎上分別選取不同的m的取值開展三軸壓縮排水和不排水數值試驗,模型參數如表1 所示。
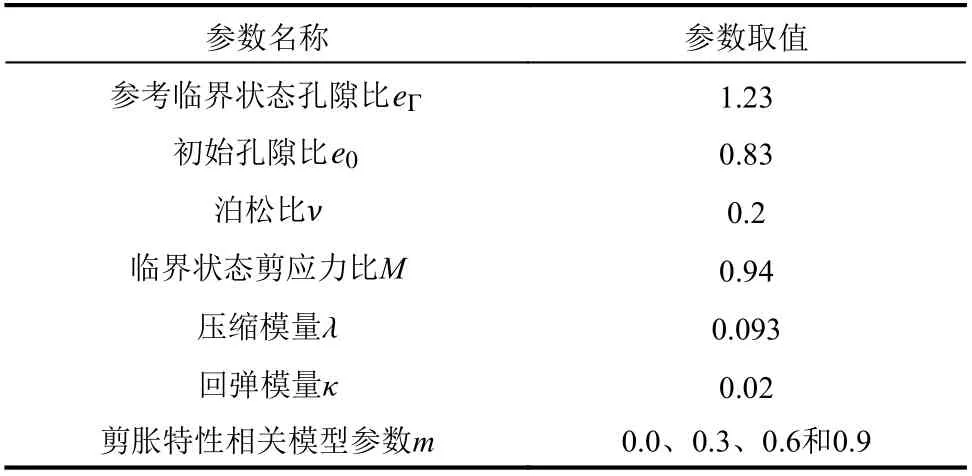
表1 模型參數敏感性試驗材料參數Table 1 Parameters used in model sensitive analysis
模型參數m對超固結重塑土的三軸壓縮排水試驗模型計算結果的影響如圖4 所示。根據圖4(a),該試樣的峰值強度隨著m值的增大而減小,體應變的剪脹量則逐漸增大。圖4(b)給出了不同m值對材料剪脹曲線的影響,可以看出,隨著m值的增大,該試樣的剪脹應力比Md逐漸減小,而m不會對材料的臨界狀態剪應力比產生影響。
模型參數m對超固結重塑土的三軸壓縮不排水試驗模型計算結果的影響如圖5 所示。根據圖5(a),該試樣的不排水抗剪強度隨著m值的增大而減小,隨著m值的進一步增大,材料的不排水抗剪強度甚至會小于其臨界強度,該現象與密實砂土的應力-應變曲線變化特點具有某種相似性[22]。圖5(b)給出了m對該試樣的應力路徑的影響。
3 模型驗證
為了進一步驗證本文所建立的分數階下加載面模型的適用性,采用該模型分別對Black Kaolin黏土[39]和Fujinomori 黏土[29]的三軸壓縮試驗結果進行模擬,重點探究土體超固結性對其剪脹特性的影響,模型參數如表2 所示。
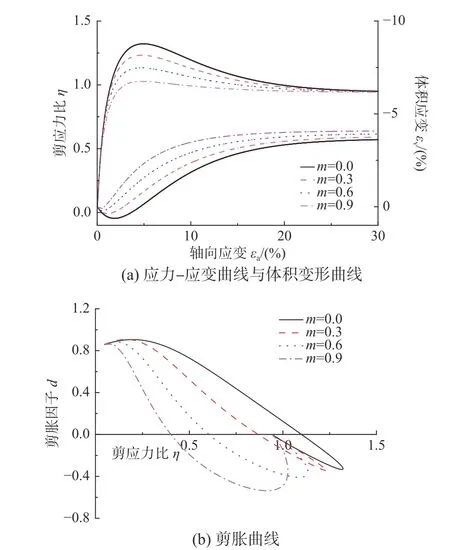
圖4 參數m 三軸壓縮排水試驗模型計算結果的影響Fig. 4 Effect of parameter m on drained triaxial test model predictions
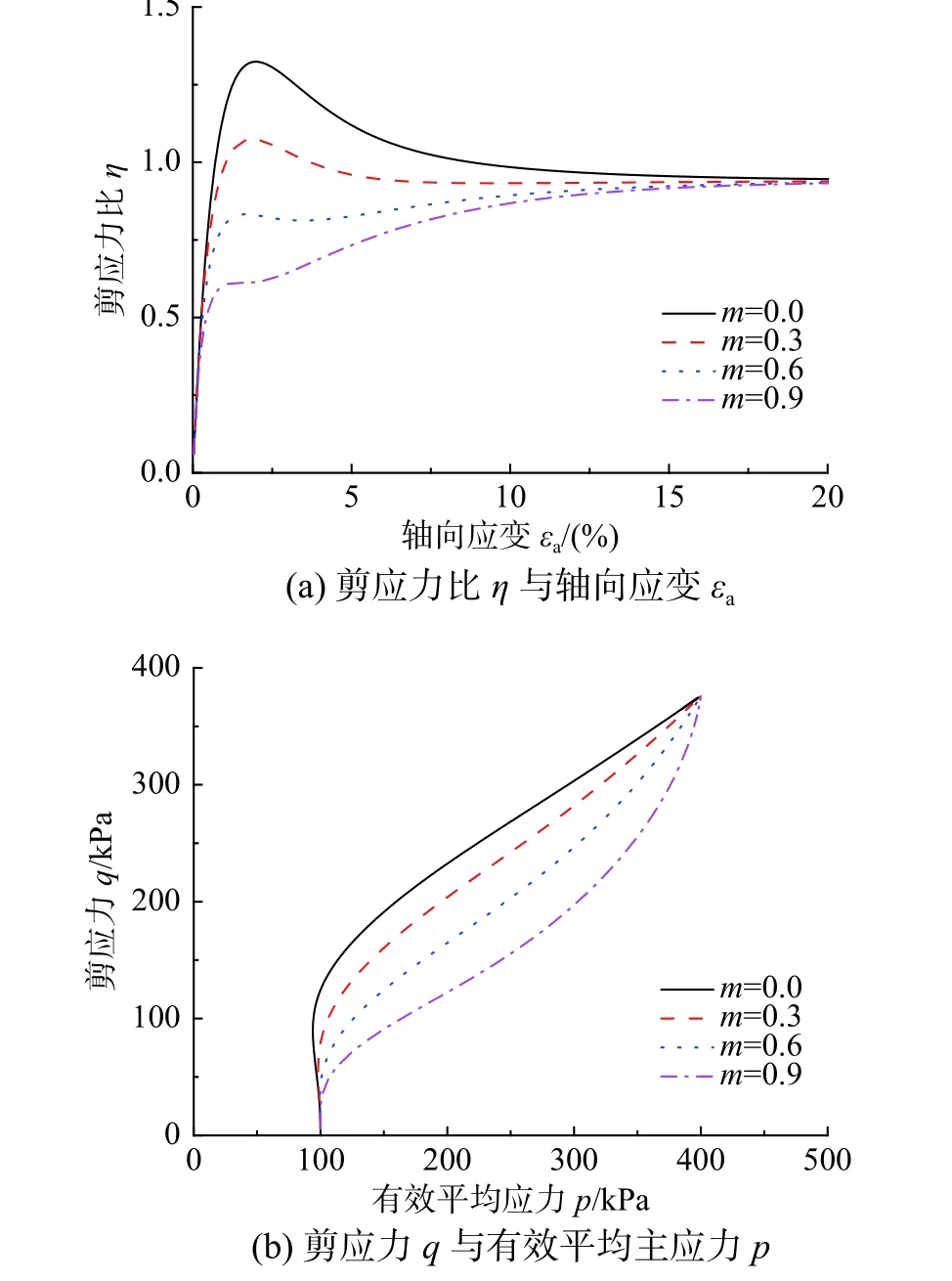
圖5 參數m 三軸壓縮不排水試驗模型計算結果的影響Fig. 5 Effect of parameter m on undrained triaxial test model predictions
圖6 給出了Black Kaolin 黏土的三軸壓縮排水試驗結果和模型計算結果,其中,Black Kaolin 黏土的加載圍壓分別為100 kPa、200 kPa、400 kPa和800 kPa,且OCR分別為8、4、2 和1。在不同的圍壓下,Black Kaolin 黏土的初始孔隙比e0分別為1.09、1.06、0.94 和0.91。根據圖6(a)和圖6(b),模型計算結果與試驗結果具有良好的相關性。當OCR=8 時,由于應力歷史的影響,Black Kaolin黏土的應力-應變曲線表現出明顯的應變軟化特點;在加載的初始階段,土體的孔隙比e逐漸減小,產生剪縮變形,隨著剪切破壞的進一步發生,e開始反向增加并伴隨著剪脹現象的發生。Black Kaolin 黏土在不同圍壓下的剪脹曲線如圖6(c)所示,可以看出土體的剪脹應力比Md隨著OCR的增大而增大,同時在OCR=4,8 的情況下,土體會發生明顯的剪脹變形。進一步,圖7 給出了本文模型對Fujinomori 黏土的平均主應力一定的三軸壓縮試驗結果的模擬結果,其中,Fujinomori 黏土的平均主應力分別為98 kPa、196 kPa、196 kPa 和196 kPa,且OCR分別為8、4、2 和1。在不同的圍壓下,Fujinomori 黏土的初始孔隙比e0分別為0.727、0.713、0.76 和0.81。根據圖7(a)和圖7(b),可以看出本文模型能夠較好的描述Fujinomori 黏土的應力-應變和體積變形特點。當OCR=8 時,本文模型計算得到的峰值強度所對應的軸向應變明顯偏大,存在20%左右的誤差,此時計算得到的體應變剪脹量也相應偏大。值得注意的是,相比常規的三軸壓縮不排水試驗,在平均主應力一定的情況下,模型計算得到剪脹曲線呈現出完全不同的變化特點。如圖7(c)所示,在加載的初始階段,剪脹因子d會逐漸增大,在達到峰值后反向減小,當OCR大于1 時,d會減小至負值,此時土體發生剪脹破壞,隨著OCR的增大,該趨勢將更加明顯。
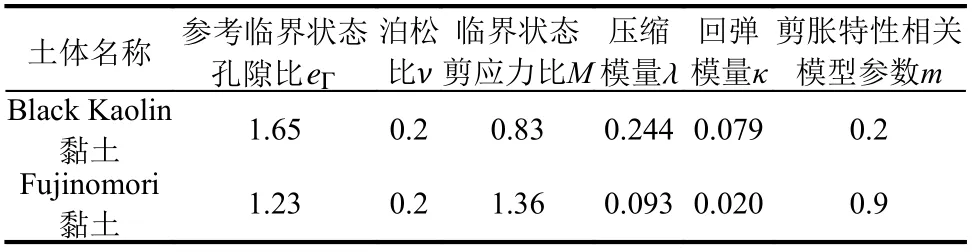
表2 模型參數敏感性試驗材料參數Table 2 Parameters used in model sensitive analysis
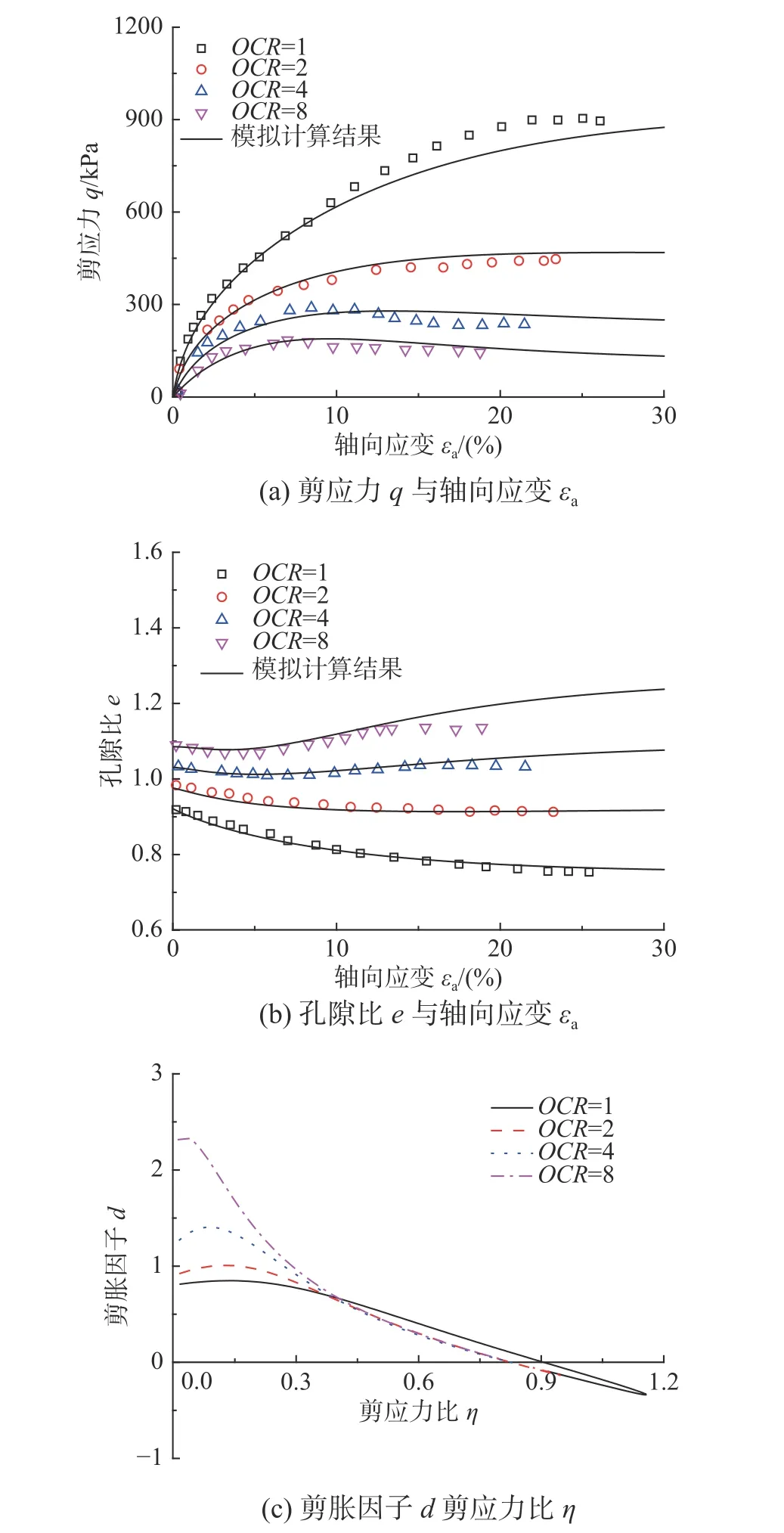
圖6 Black Kaolin 黏土試驗結果與模型計算結果對比Fig. 6 Comparison between experimental data and model predictions of Black Kaolin clay
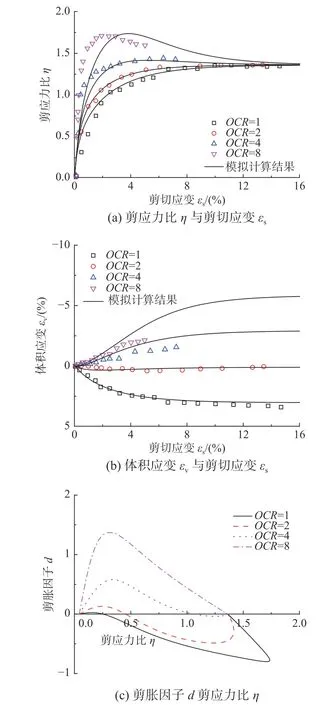
圖7 Fujinomori 黏土試驗結果與模型計算結果對比Fig. 7 Comparison between experimental data and model predictions of Fujinomori clay
從上述分析可以看出,本文建立的模型能夠合理地反映超固結重塑土的應變軟化和剪脹特性,進而對土體應力-應變和體積變形特點進行準確的描述。此外,本文模型的計算結果表明,超固結性會對土體的剪脹特性產生影響。
4 結論
本文基于Caputo 微分方法提出了分數階應力誘導剪脹方程以考慮超固結性對土體剪脹特性的影響,在此基礎上引入了下加載面的力學概念,從而建立了適用于超固結重塑土的分數階下加載面模型。通過將模型計算結果與試驗結果進行對比分析,初步驗證了該模型的合理性,主要結論有:
(1)基于 Caputo 分數階微分方法,可以在不引入塑性勢函數的情況下得到一個新的分數階塑性流動法則,該流動法則能夠合理地描述塑性流動方向與土體屈服面之間的非正交性,進而統一地描述相關聯和非相關聯的塑性流動法則。
(2)基于分數階塑性流動法則,可以給出適用于黏土的分數階應力誘導剪脹方程。由于分數階數是關于表征超固結程度的相似因子的函數,因此本文提出的剪脹方程能夠考慮超固結性對黏土剪脹特性的影響。
(3)通過引入下加載面的力學概念并且給出相應的硬化法則,本文所建立的分數階下加載面模型能夠準確地描述超固結黏土的應變軟化和剪脹特性。相比較 MCC 模型,本文模型僅額外地引入了一個與土體剪脹特性有關的材料參數。

