扣壓力失效狀態下WJ-8 扣件垂向力學行為研究

高 亮，趙聞強，侯博文

(北京交通大學土木建筑工程學院，北京 100044)

高速鐵路無砟軌道扣件系統聯結了鋼軌與下部無砟軌道，并傳遞列車動載至下部無砟道床。扣件系統工作時主要通過螺栓、道釘壓緊彈條，使之發生形變并扣壓鋼軌，從而起到了保持鋼軌穩定幾何形位的功能。但隨著運營時間的增長，扣件系統服役狀態的劣化不可避免。在循環動荷載和其他長期環境荷載的作用下，扣件會逐漸出現扣壓力損失、彈條松動松脫等現象。退出正常工作狀態的扣件系統降低了鋼軌承載穩定性，影響了高速列車的安全、平穩運營，嚴重時甚至可能導致脫軌事故。

許多研究通過車輛-軌道耦合動力學理論建立了相關動力學模型來評估扣件失效對車輛-軌道系統動力響應特性的影響。肖新標等[1]等基于輪軌耦合動力學理論分析扣件失效工況下直線軌道-車輛系統的動態響應。張斌[2]運用車輛軌道系統振動分析數值方法,研究了地鐵扣件失效對軌道振動特性的影響。朱劍月[3]建立了基于連續彈性離散點支承梁的鋼軌模型，分析了列車運行速度與扣件失效數量對軌道結構動力性能的影響。余關仁等[4]等研究了扣件和隔振器失效對浮置板動力響應特性的影響。徐啟喆等[5]建立了不同失效情況的扣件模型，分析了扣件失效對鋼軌變形及轉角的影響。在上述研究中，扣件大多被簡化為多點支承的彈簧-阻尼單元，并在失效處將扣件剛度屬性折減或去掉彈簧單元來實現扣件失效的模擬，彈簧單元垂向剛度也簡化為線性。這種模擬方式可以用來模擬扣件墊板脫出的失效場景，但不適用于扣件處于扣壓力失效的情況。針對扣壓力失效，應選擇更合適的模型來描述其失效后的垂向非線性力學行為。

Oregui 等[6]建立了不同類型的扣件簡化模型，研究了扣件模型建模方式對單節軌枕軌道垂向動力學的影響；王開云等[7]考慮扣件系統扣壓件的預壓力，建立了扣件垂向動力分析模型，分析了扣件垂向振動特性。這些研究建立了更加精細的扣件模型[8]，為本文研究扣件的垂向非線性行為提供了一定的思路，但在代入車輛-軌道大系統計算時也存在計算代價較大等問題。針對高速鐵路扣件斷裂的問題，朱勝陽、尚紅霞等[9 ? 10]還通過非線性接觸理論建立扣件實體模型，從結構本身探究了扣件斷裂的原因，這亦為本文提供了方法上的參考。

本文以目前應用較為廣泛的高速鐵路CRTSIII型板式無砟軌道及其配備的有擋肩扣件WJ-8 扣件系統為例，通過建立扣件系統的精細化分析模型揭示了扣件扣壓力失效后自身的垂向非線性力學行為；提出了扣件扣壓力失效的簡化模擬方法，使之既能保證原有車軌模型中扣件簡化模型的計算效率，也能夠反映一定的垂向非線性剛度特征；最后分析了不同失效類型對車輛-軌道系統動力響應的影響。本文的計算結果能夠為高速鐵路扣件結構優化、扣件病害檢測等領域提供一定的理論參考。

1 WJ-8 扣件精細化分析模型

1.1 扣件系統部件的精細化模擬

基于材料彈塑性本構和非線性接觸理論，本文采用ABAQUS 軟件對扣件系統進行精細化建模。WJ-8 扣件系統由螺旋道釘、平墊圈、彈條、絕緣塊、軌距擋板、軌下墊板、鐵墊板、鐵墊板下彈性墊板以及定位于下部軌道混凝土中的預埋套管組成[11]，如圖1 所示。具體建模時，鋼軌為CHN60 鋼軌，軌距擋板采用7 號軌距擋板，螺旋道釘和絕緣塊分別選用S2 型螺旋道釘和WJ8-Ⅰ型絕緣塊。鋼軌、道釘、絕緣軌距塊等部件采用線性減縮六面體單元進行建模。WJ-8 扣件彈條可分為W1 型和X2 型。本文選用W1 型彈條，并采用改進的二次四面體單元進行建模以保證計算的收斂性和準確性，每根彈條包含26421 個單元。

圖1 WJ-8 扣件系統主要部件組成Fig. 1 Main components of WJ-8 fastener

WJ-8 扣件系統通過鐵墊板下彈性墊板為系統提供必要的彈性[12 ? 13]。本文以適用于高速線路的B 類鐵墊板下彈性墊板為例，其墊板靜剛度取為23 kN/mm(±3 kN/mm)，扣件整體節點靜剛度相應取為30 kN/mm(±10 kN/mm)。模型考慮墊板靜剛度屬性及面支承效應，在鐵墊板下采用三向彈簧-阻尼單元模擬彈性墊板，且為垂向為只受壓彈簧。

WJ-8 扣件系統精細化分析模型考慮了彈條等金屬部件的理想彈塑性材料本構，并采用雙線性強化模型對其彈塑性行為進行描述[14]，其應力-應變關系可概括為：

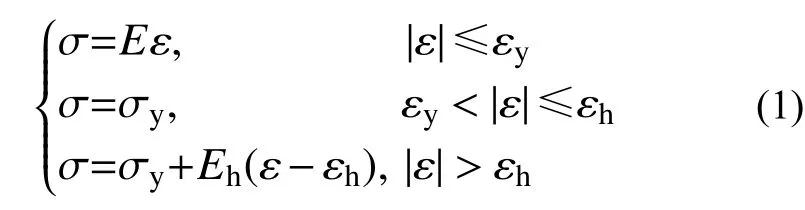
式中：E是彈性模量；Eh為強化模量；σy和εy分別是屈服應力和屈服應變。

當材料進入塑性狀態后，試件橫截面積的變化對材料性能的影響不能被忽視。因此在定義雙線性強化模型時，需要將工程應力-應變數據轉換為有限變形中面積改變的真應力-應變曲線：

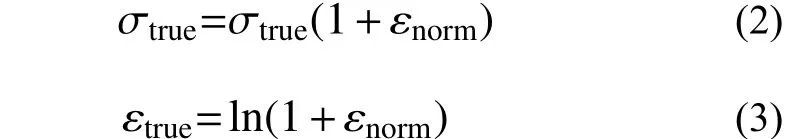
式中：σtrue和εtrue為分別為真實應力和真實應變；σnorm和εnorm分別為名義應力和名義應變。

扣件精細化分析模型的具體建模參數見表1。

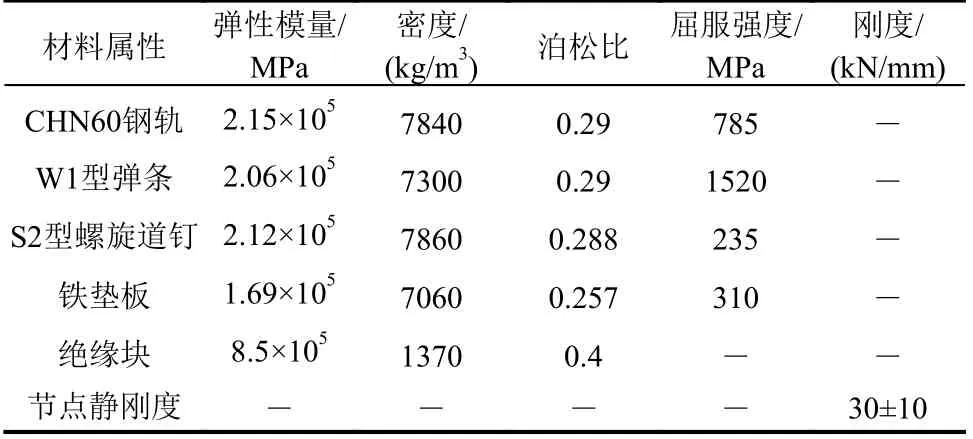
表1 WJ-8 扣件精細化分析模型建模參數Table 1 Model parameters of WJ-8 fastener model

1.2 扣件系統復雜接觸關系的模擬

WJ-8 扣件系統各部件間通過一定的接觸關系相互配合來保證其正常工作性能。WJ-8 扣件中的接觸關系較為復雜，模型中將所有部件間的接觸行為離散為法向與切向兩類，法向的接觸行為通過式(4)定義，認為接觸面之間的法向接觸力只存在壓力，且兩者不允許侵入、貫穿；切向則采用簡化的庫倫摩擦模型。參照既有研究和相關技術條件[15 ? 17]，模型中需設置的接觸對關系見表2。

表2 WJ-8 扣件精細化分析模型接觸對設置Table 2 Contact pair of WJ-8 fastener model

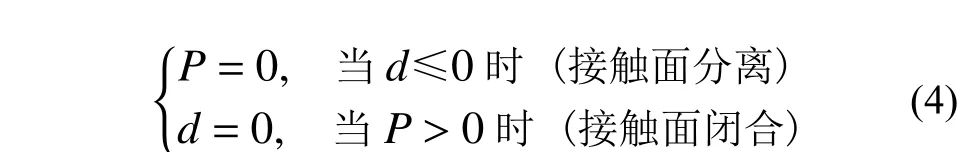
式中：P代表接觸應力；d代表了接觸面間的間隙，正值表示分離，負值表示侵入。

WJ-8 扣件精細化分析模型通過在螺栓道釘頂部施加一定的緊固壓力扣緊彈條，使之達到正常工作狀態如圖2 所示。

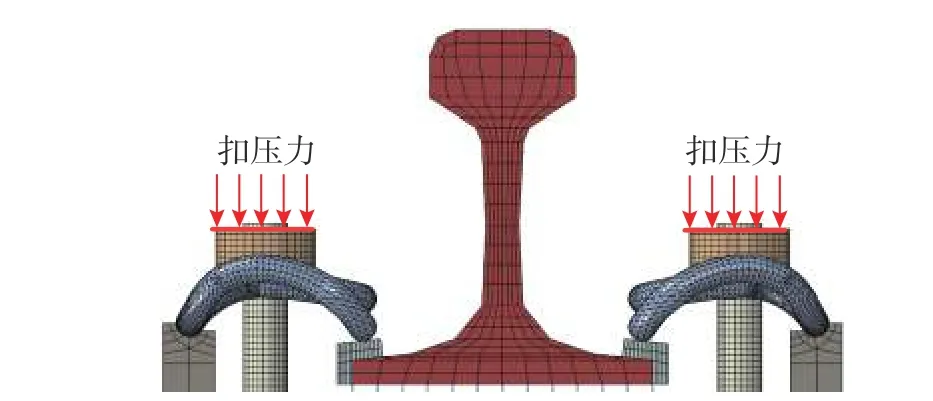
圖2 WJ-8 扣件精細化模型中扣壓力施加方式Fig. 2 Clamping force loading in WJ-8 fastener model

圖2所示的扣壓力模擬方式既能夠再現彈條的緊固過程[18]，也方便了后續彈條扣壓力及彈程的驗證。模型在鋼軌端部約束其縱向變形，對絕緣塊、軌距擋板等結構約束了其橫向變形，在保障計算精度的基礎上提高了計算效率。

1.3 模型有效性驗證

本節對扣件精細化分析模型的有效性進行驗證，以確保模型能夠準確反映WJ-8 扣件系統的工作特征。對所建立的扣件分析模型施加安裝荷載后，發現彈條位移為14 mm 時，鋼軌位移達到0.574 mm，此時換算得到單個彈條扣壓力為9.28 kN，彈條與絕緣塊間隙為0.42 mm，符合扣件設計要求中單個W1 型彈條扣壓力大于9 kN，彈程14 mm，彈條與絕緣塊間隙不大于0.5 mm 的規定[17, 19]。

獲取扣壓力-彈程曲線如圖3(a)所示。由圖3(a)可知，彈條在14 mm 左右達到“三點接觸”狀態；“三點接觸”狀態前后，彈條扣壓剛度分別為0.66 kN/mm 和4.90 kN/mm，與文獻[15, 20]中W1 型彈條的扣壓力-彈程曲線較為吻合。

此外，對鋼軌軌頭施加垂向荷載，其荷載-位移曲線如圖3(b)所示，計算可得此時扣件節點靜剛度為31.30 kN/mm，驗證了模型的有效性。

2 WJ-8 扣件垂向力學行為分析

2.1 扣件受力階段分析

提取車輛軌道動力模型計算得到的典型扣件力垂向曲線如圖4 所示。

由圖4 可知，扣件在受力時可分為受拉階段和受壓階段，根據作用時間的不同，又可將其過程概括為圖5 所示的A、B 兩個階段。

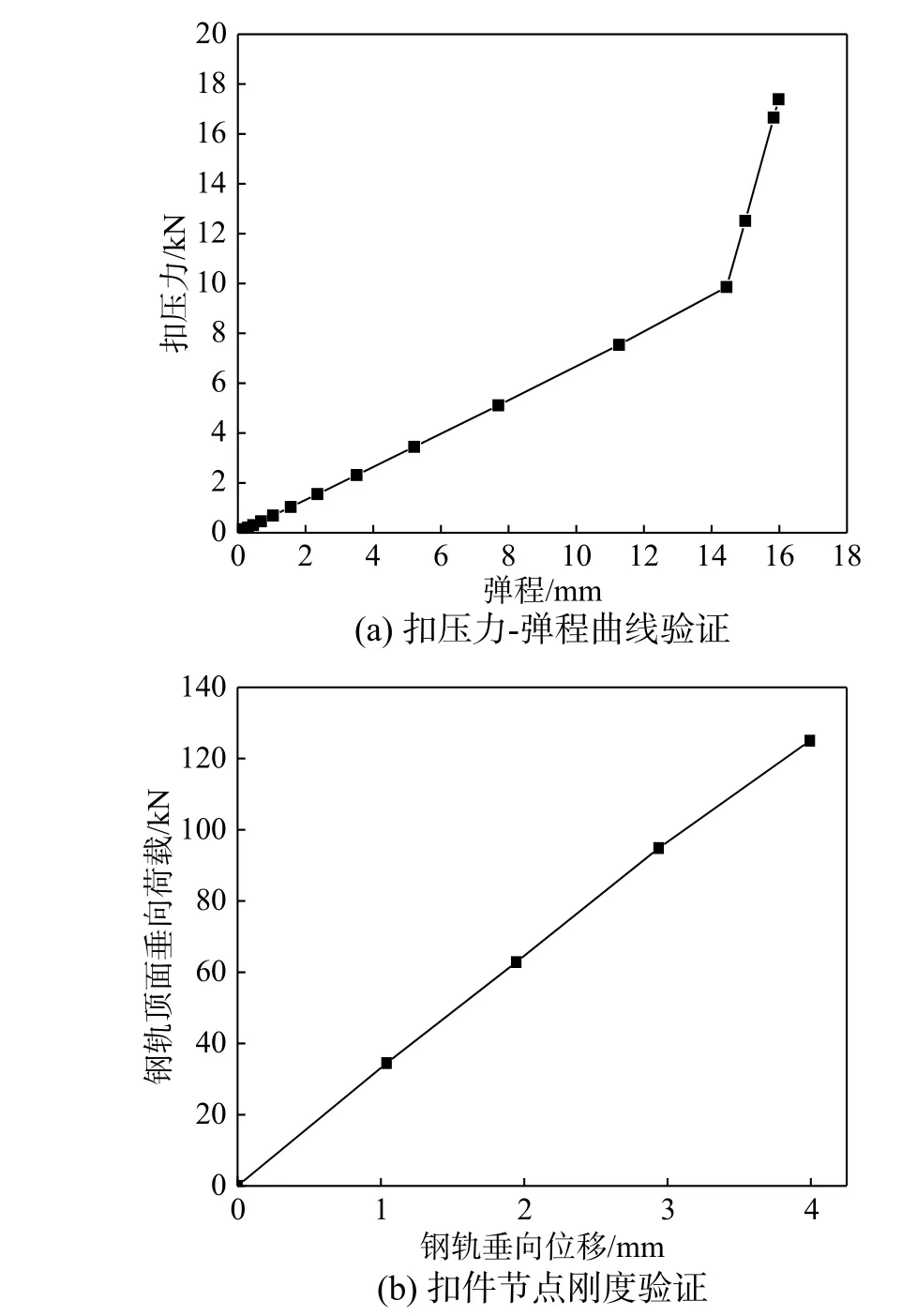
圖3 扣件精細化模型有效性驗證Fig. 3 Validation of WJ-8 fastener model

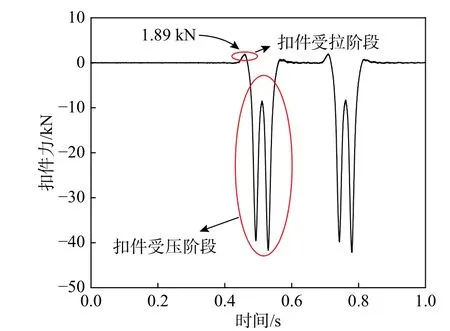
圖4 典型垂向扣件力時間歷程曲線Fig. 4 Typical time history of vertical fastener force

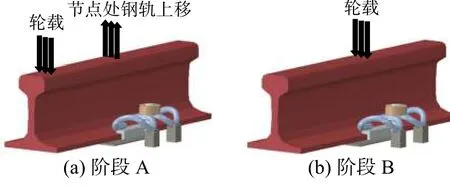
圖5 兩種典型扣件受力階段Fig. 5 Two typical loading phase of fasteners

在階段A 輪載作用于扣件節點之間，在輪載的作用下該處鋼軌出現向下的位移，因鋼軌自身抗彎剛度，此時扣件節點處有上移的趨勢，此時扣件承受拉力[21]。在階段B 輪載逐步靠近扣件節點位置并作用于節點上方，此時扣件承受壓力；而后輪載向前移動，扣件受力又回到階段A。

當扣件系統正常工作時，扣壓件將鋼軌固定在承軌臺上，使得鋼軌具有抵抗上拔力的能力不致出現過大的上移。當扣件扣壓件失效后，如扣件彈條斷裂飛出，此時扣件的整體抗拉能力將大大減小。

為了量化評價這種限制鋼軌向上位移的能力，本文將扣件的抗拉抗壓剛度獨立開來，并將扣件失效模式分為不失效、扣壓力失效和完全失效三類。扣壓力失效指扣件彈條斷裂或扣壓力喪失，此時扣件限制鋼軌上移的能力極小，但節點抗壓剛度Kc正常；完全失效模式則與文獻[2 ? 4]類似，軌下墊板已經脫出，鋼軌底部無支承。根據扣件不同階段的受力特征可知，求出扣件系統的整體抗拉剛度Kt，是區分三種失效模式的關鍵。

2.2 扣件扣壓力失效后的垂向非線性行為

為確定扣件整體抗拉剛度Kt，本文利用所建立的扣件精細化分析模型，將上拔力施加在鋼軌底面如圖6 所示。借鑒靜剛度測試方法的思路，加載過程中假定上拔力在鋼軌底面均勻分布，加載區域為墊板范圍。將扣件抗拉剛度定義為：

式中：F為上拔力；u為鋼軌頂面的垂向位移。

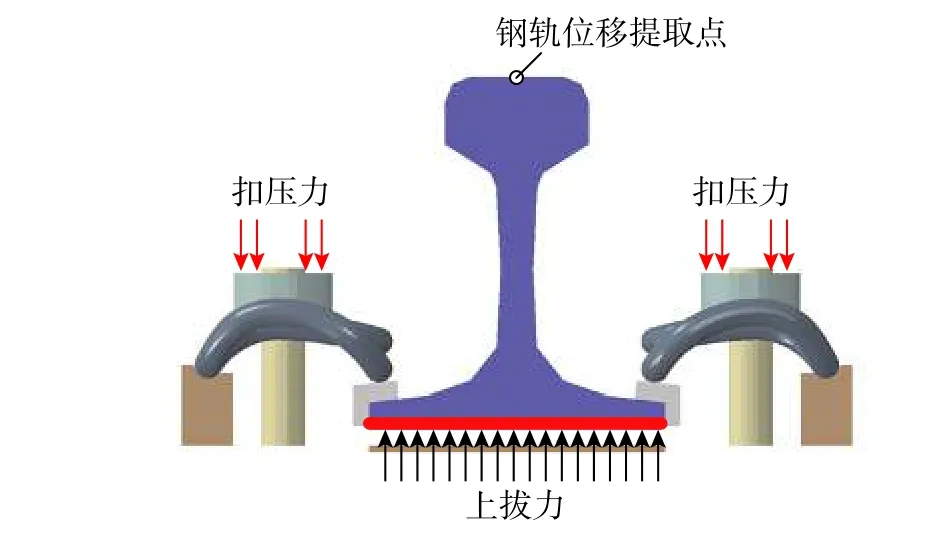
圖6 扣件抗拉剛度數值試驗加載示意Fig. 6 Loading of numerical test for tensile stiffness of fastener

提取如圖6 所示位置的鋼軌頂面位移，獲取上拔力-位移曲線如圖7 所示。

當彈條扣壓力未損失時，兩根彈條所提供的扣壓力Fc為18 kN。由圖7 可知，上拔力-位移曲線存在明顯的雙線性特征，當上拔力為18 kN時，鋼軌向上的垂向位移為0.54 mm，此時、Kt為33 kN/mm，與扣件節點抗壓剛度Kc相差不大；當上拔力超過18 kN 后，上拔力-位移曲線出現了明顯的“屈服”階段，上拔力超過22 kN 時，Kt顯著降低，約為0.44 kN/mm，對鋼軌上移基本無約束作用。

圖7 WJ-8 扣件上拔力-位移曲線Fig. 7 Uplift force-displacement curve of WJ-8 fastener

為探究Kt出現這種“屈服”現象的原因，提取彈條塑性應變峰值與對應鋼軌垂向位移的關系曲線如圖8 所示。由圖8 可知，塑性應變-位移曲線與上拔力-位移曲線趨勢基本一致，出現了明顯的雙線性特征。其塑性應變的發展特征與彈條在上拔過程的變形特征息息相關。如圖9 所示，當上拔力未超過18 kN 時，彈條中肢存在的殘余扣壓力使得彈條對鋼軌仍有較好的限制能力，并使得中肢與彈條前肢的相對位移逐漸增大，中肢與前肢間存在的非協調變形使得尾肢中部塑性應變迅速增長。

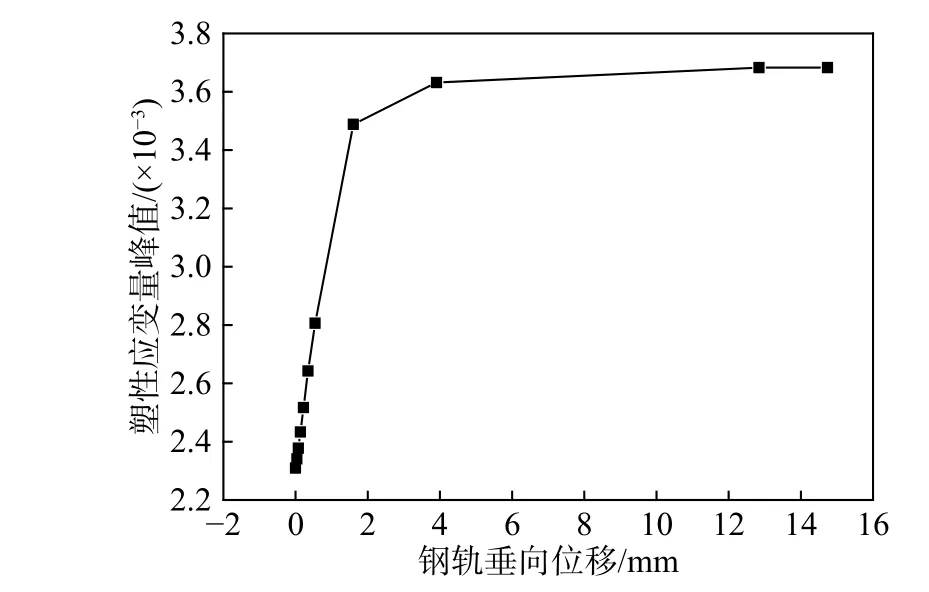
圖8 WJ-8 扣件塑性應變量峰值-位移曲線Fig. 8 Peak plastic strain-displacement curve of WJ-8 fastener

此外，此時彈條與絕緣塊間一直處于“三點接觸”狀態，傳力關系較先前發生了改變，彈條處于偏心受力的狀態，故此時的Kt較先前的彈條前端扣壓剛度稍低。當上拔力增長至兩根彈條提供的扣壓力時，此時彈條變形趨勢轉為整體外翻，對鋼軌的限位能力大大減弱，其塑性應變也不再發展。

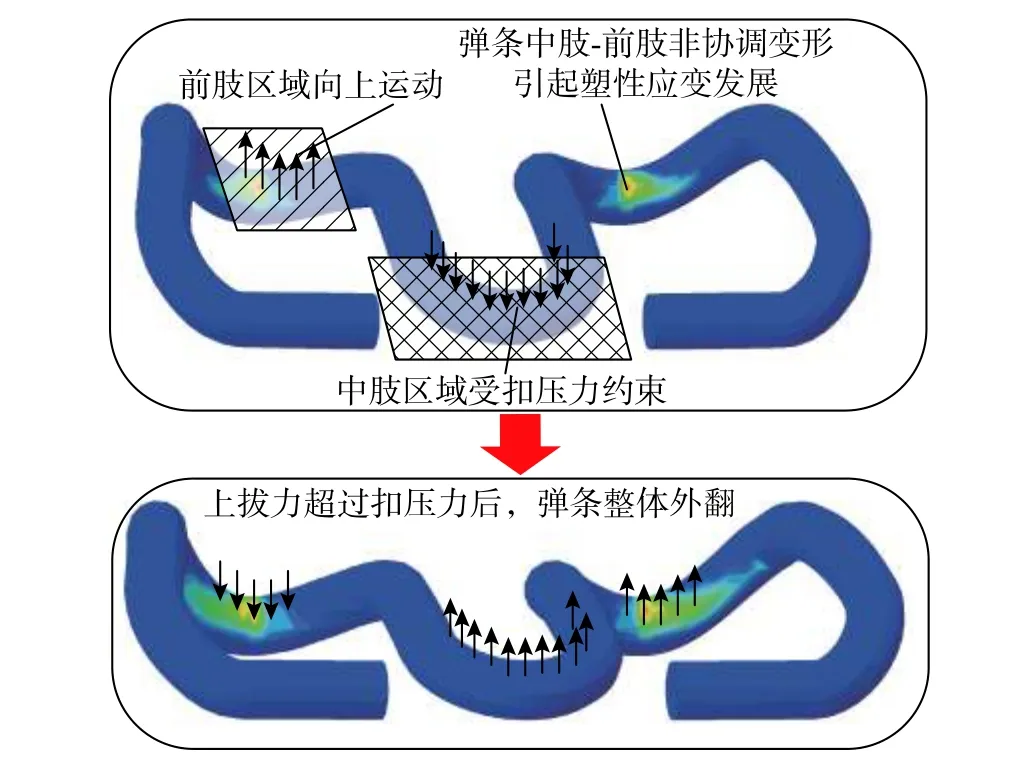
圖9 WJ-8 扣件雙線性上拔剛度發生機理Fig. 9 Mechanism of bilinear uplift stiffness of WJ-8 fastener

為明確彈條扣壓力損失對扣件整體抗拉剛度Kt的影響，分別考慮扣壓力損失25%、50%和75%的情況，采用相同的加載方式，獲取不同扣壓力下的上拔力-位移曲線如圖10 所示。

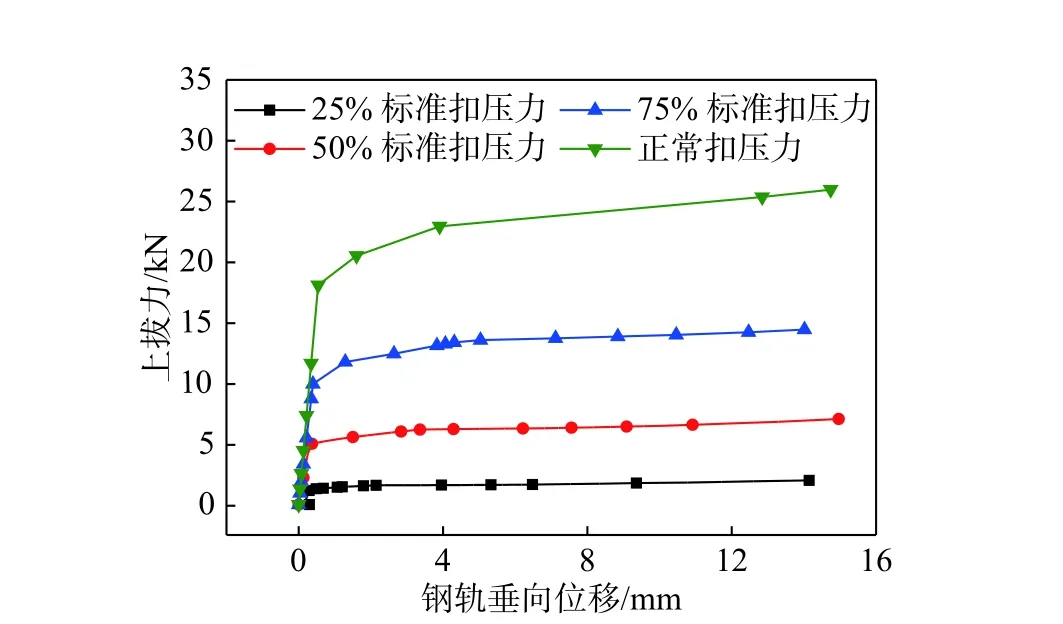
圖10 不同扣壓力條件下上拔力-位移曲線Fig. 10 Uplift force-displacement curve under different clamping force

由圖10 可知，當扣壓力出現損失后，上拔力-位移曲線更早地到達“屈服”階段，即扣壓力的損失使得Kt更快到達低剛度階段。當彈條扣壓力只剩原來的50%時，上拔力達到9 kN 后曲線就出現拐點。

2.3 扣件扣壓力失效在車輛-軌道耦合模型中的簡化表達

既有的車輛軌道動力學模型采用彈簧-阻尼單元模擬扣件的垂向剛度行為時，將其簡化為如圖11(a)所示的線性剛度彈簧[22 ? 23]，即假定扣件的抗拉剛度與受壓剛度一致。本文在傳統線性剛度彈簧的基礎上進行改進，基于扣件精細化模型的結果對扣件垂向非線性剛度行為[24 ? 25]進行修正。

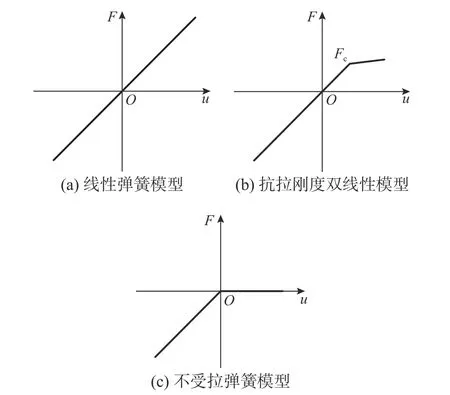
圖11 不同扣件垂向剛度模型Fig. 11 Different vertical stiffness models of fasteners

由2.3 節可知，扣件的抗拉剛度存在非線性特征。基于此，本文提出了如圖11(b)所示的抗拉剛度雙線性模型。在抗拉剛度雙線性模型中，當扣件承受壓力時，此時扣件彈簧剛度與節點抗壓剛度Kc一致(即F<0，K=Kc)；當扣件彈簧轉入受拉狀態，但所承受的上拔力未超過扣壓力，此時可認為扣件抗拉剛度與節點剛度一致(即Fc>F>0，K=Kt=Kc)；當上拔力超過了扣件的扣壓力后，認為扣件限制鋼軌上移的能力基本消失，此時設置彈簧的抗拉剛度為0(即F>Fc，K=Kt=0)。

當扣件扣壓力全部失效時，在抗拉剛度雙線性模型的基礎上本文還提出了如圖11(c)所示的不受拉彈簧模型，扣件彈簧不提供抗拉剛度(即F>0，K=Kt=0)。

3 不同扣件失效類型對車軌動力系統的影響研究

3.1 車輛-軌道耦合動力模型

為評估不同扣件失效類型對車軌動力響應特性的影響，本文基于多體動力學理論和有限元方法建立了車輛-軌道耦合動力模型(見圖12)，并通過ABAQUS 軟件將其實現。將車輛視為由車體、轉向架及輪對組成的多剛體系統，轉向架-輪對、車體-轉向架間采用三向彈簧-阻尼單元模擬一系、二系懸掛。模型分別考慮車體、轉向架6 個自由度，輪對5 個自由度共計38 個自由度。車輛采用CRH3型車，建模參數參見文獻[26]。

軌道模型選取CRTSⅢ型板式無砟軌道，包括鋼軌、扣件、軌道板、自密實混凝土層、底座板。鋼軌及下部軌道結構均采用實體單元進行建模，將軌道板與自密實混凝土共節點建模以表征其黏結關系良好；自密實混凝土層與底座間存在土工隔離層，建模時通過接觸單元模擬，切向考慮為一定的摩擦作用；底座上設置兩個尺寸為0.6 m×0.4 m 的凹槽，凹槽四周設有彈性墊層，建模時考慮為線性接觸剛度[27]。扣件仍然考慮為多根三向彈簧-阻尼單元[28]。扣件垂橫向剛度分別取30 kN/mm及25 kN/mm[20]，縱向阻力取15 kN/組。當涉及到不受拉彈簧時，將彈簧垂向設置為僅受壓的模式。CRTSⅢ型板式無砟軌道其他具體參數參見文獻[29]。

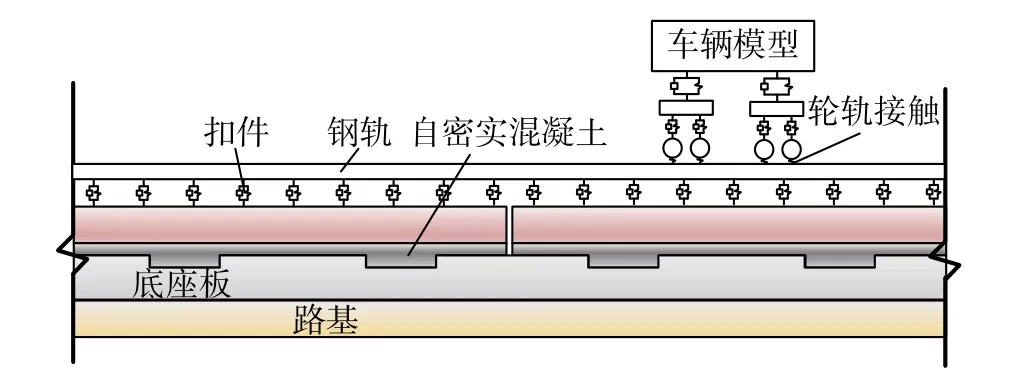
圖12 車輛-軌道耦合動力模型Fig. 12 Vehicle-track coupling dynamic model

建立輪軌接觸時將其離散為法向與切向的接觸行為，法向接觸力采用如式(7)所示的赫茲非線性理論進行計算如式所示；切向則采用簡化的庫倫摩擦模型，摩擦系數取為0.3。模型通過罰函數法將法向、切向接觸條件引入泛函方程中進行求解。輪軌隨機不平順與文獻一致，采用《高速鐵路無砟軌道不平順譜》推薦的隨機不平順，波長范圍取2 m～200 m。模型總長度為120 m。

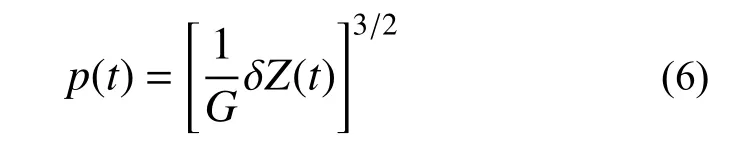
式中：G/(m/N2/3)表示輪軌接觸常數； δZ(t)表示輪軌間的彈性壓縮量；t表示時間。本文采用磨耗型車輪踏面，輪軌常數G采用下式進行計算。

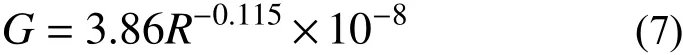
式中，R表示車輪滾動圓半徑

3.2 扣件扣壓力失效與完全失效對車輛軌道系統動態響應的影響

本節主要分析了扣件不同失效模式對車輛軌道系統動態響應的影響。分析前首先基于雙線性抗拉剛度彈簧模型建立了正常狀態的扣件，扣件提供的扣壓力(Fc=18 kN)，并與線性剛度彈簧模型的計算結果進行了對比如圖13 所示。

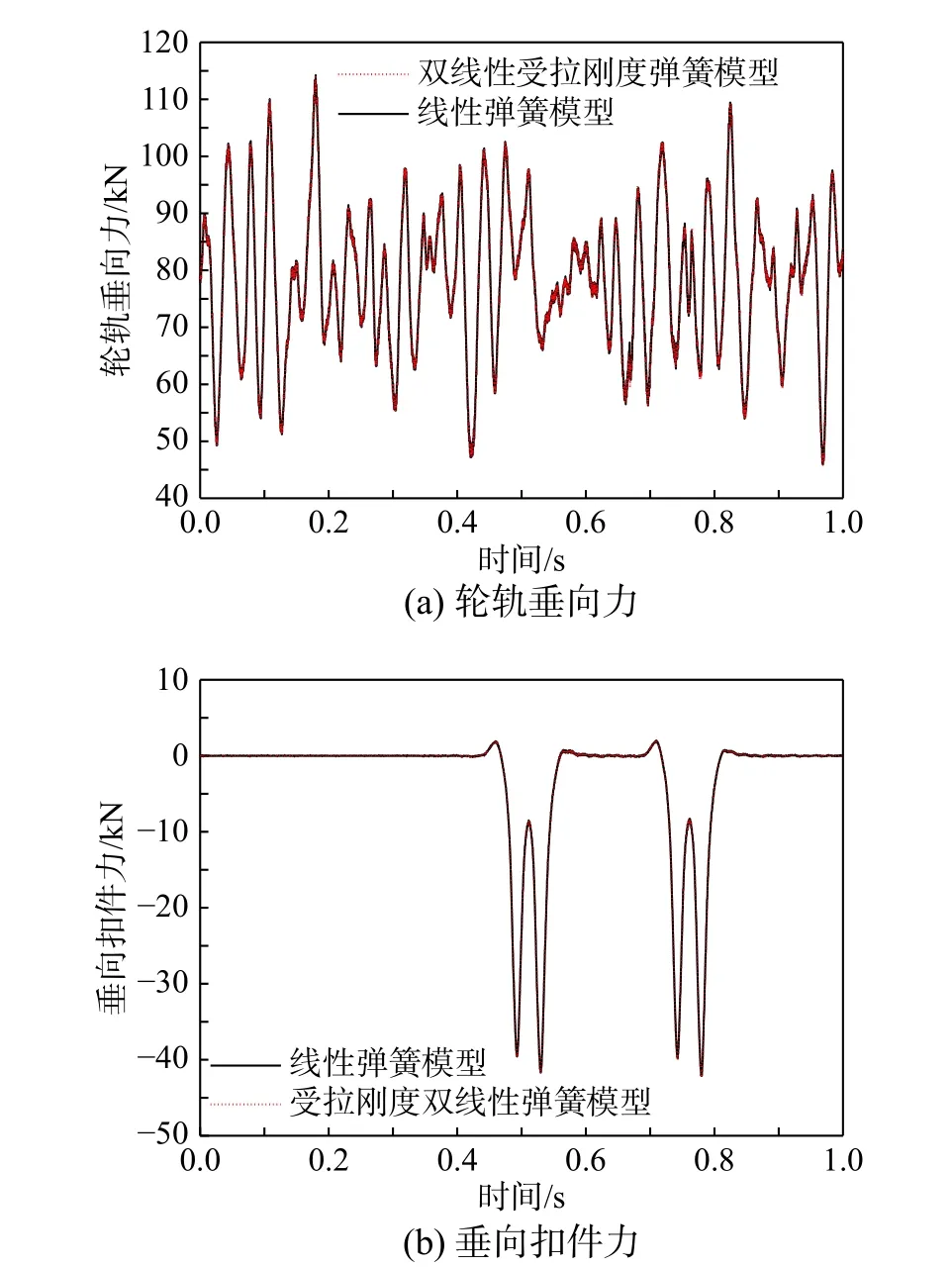
圖13 線性剛度彈簧模型與雙線性抗拉剛度彈簧模型動力響應對比Fig. 13 Comparison of dynamic response of linear stiffness spring model and bilinear tension stiffness spring model

由圖13 可知，扣件在正常工作狀態下，線性剛度彈簧模型與雙線性抗拉剛度彈簧模型的結果基本無差異，這是因為在車輛行駛過程中扣件彈簧單元所承受的上拔力并未超過扣件的扣壓力，扣件仍能提供較好的抗拔剛度。這也說明在進行動力學建模時，如不考慮扣件病害，將其簡化為線性剛度彈簧也是合理的。

考慮到扣件在實際中所受上拔力大約在1 kN～4 kN，相當于扣壓力損失77.8%～94.4%后扣件系統才有可能在車輛荷載影響下進入弱剛度階段。這時扣件的工作狀態已經接近彈條斷裂完全損失扣壓力的情況。因此在具體分析時，本文只考慮扣壓力失效和完全失效兩種扣件失效類型。扣壓力失效時扣件彈條已經斷裂，扣壓力已完全損失，但墊板仍處于原位提供抗壓剛度，模型中采用了不受拉彈簧模型來模擬失效扣件；模擬完全失效時與既有研究[1 ? 5, 23]類似，將失效扣件調整為無剛度的彈簧。高速鐵路現場調研情況表明，扣件彈條傷損區段相對集中且連續出現，且大多集中在一股鋼軌上。因此設置計算工況時綜合既有研究及現場情況，同時便于區分、放大不同失效類型的具體影響，設置了五個扣件連續失效的場景如圖14 所示。

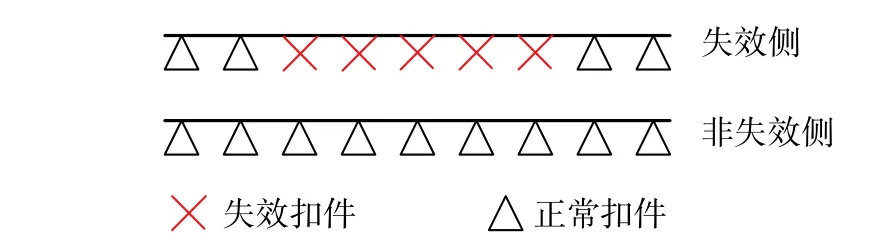
圖14 扣件失效計算工況設置Fig. 14 Fastener failure calculation conditions

以車輛運行速度250 km/h 為例，對比不同扣件失效類型與正常線路的動力響應時如圖15 所示。

圖15(a)為CRH3 型車第一輪對在失效側和非失效側的輪軌垂向力。由圖15(a)可知，扣件扣壓力失效情況下，由于軌下仍存在支承效應，輪軌垂向力與正常線路相比無明顯差異。但扣件完全失效后對輪軌力的影響更為顯著。具體而言，在進入扣件失效區域時，由于軌下剛度銳減，失效側輪軌力首先發生減載，而后出現較為劇烈的波動。扣件完全失效后，輪軌力最大可達181 kN，最小值已接近0 kN，輪重減載率已遠遠超過安全限值。由圖15(b)可知，相對失效側，對側的輪軌力差異較小，扣件失效對輪軌動態行為的影響主要集中在失效側。

圖15(c)和圖15(d)分別顯示了失效側和非失效側的垂向扣件力。由圖15(c)可知，扣件扣壓力失效時，失效側扣件垂向力峰值無明顯變化，但放大扣件力曲線可知，彈條斷裂后扣件系統已經不再承受鋼軌帶來的上拔力。圖15(d)結果表明，扣壓力失效時非失效側扣件力無明顯變化，但扣件完全失效后，非失效側扣件力最大值由35.74 kN增加至46.32 kN，增加了29.60%。

圖15(e)給出了失效側鋼軌的垂向位移時程曲線。由圖15(e)可知，扣件扣壓力失效時鋼軌垂向位移峰值變化不大。但放大扣件位移曲線后發現，彈條斷裂后扣件無法約束鋼軌的上翹變形，使得鋼軌的上翹位移有所增加。而扣件完全失效后，鋼軌下無支承，失效區域線路的抗彎剛度全來自于鋼軌自身，此時鋼軌垂向位移峰值由正常工況的1.31 mm 增長至12.35 mm，增加了近九倍。對側的鋼軌位移區別不大，在此不再列出。

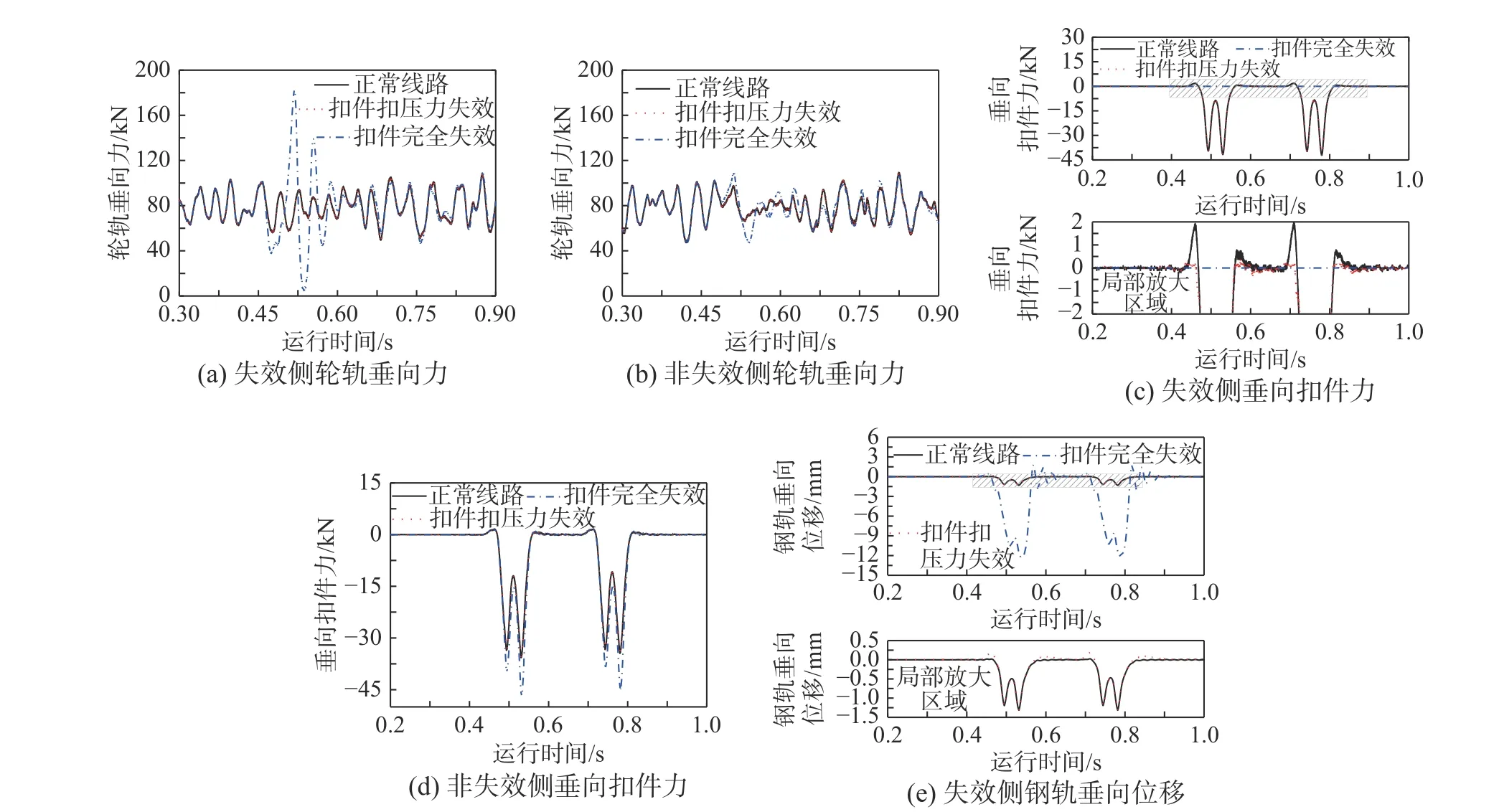
圖15 不同扣件失效類型與正常線路的動力響應時程曲線Fig. 15 Time history of dynamic response of different fastener failures and normal lines

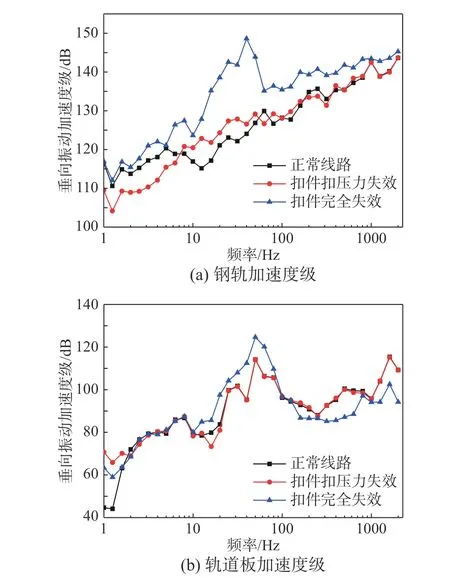
圖16 軌道1/3 倍頻程加速度級Fig. 16 1/3 octave band acceleration level of track structure

圖16 給出了鋼軌、軌道板振動加速度的1/3 倍頻程。扣件扣壓力失效和完全失效都削弱了失效區域內的鋼軌約束，結構振動特性發生了明顯改變。從圖中可知與正常線路相比，扣件處于扣壓力失效狀態時，鋼軌加速度在8 Hz～50 Hz 中心頻段范圍內有所增長，這種增長主要來自鋼軌的上翹位移。在800 Hz 中心以后，振動加速度基本無明顯差異。扣件扣壓力失效對軌道板的振動特性未產生明顯影響。

扣件完全失效時鋼軌加速度在全頻段都有所增加，其中在10 Hz～125 Hz 中心頻段范圍內出現了明顯的增長，覆蓋了當前時速下波長為單個扣件間距和6 個扣件間距時所對應的頻率。扣件完全失效后，由于鋼軌振型的影響，峰值頻率出現在中心頻率45 Hz 處。軌道板振動加速度也出現了全頻段的放大，但變化程度相對鋼軌較小。

4 結論

本文針對扣件失效在動力學模型中的模擬問題，通過建立扣件精細化分析模型，將WJ-8 扣件垂向力學行為分階段離散，提出了由節點抗壓剛度和抗拉剛度組成的簡化扣件模型，并基于彈條的變形姿態及塑性應變量解釋了扣件在承受上拔力時的非線性力學行為。在此基礎上通過車軌動力模型比較了不同扣件失效類型對車軌系統動態響應的影響。主要結論總結如下：

(1)扣件系統的受力過程可分為受壓和受拉兩個階段。扣件抗拉剛度存在雙線性特征，通過彈條塑性應變量和運動姿態解釋了彈條出現雙線性抗拉剛度的原因。扣壓力的喪失使得扣件抗拉剛度更快到達低剛度階段。

(2)在原有線彈性彈簧模型的基礎上提出了改進的抗拉剛度雙線性模型和不受拉彈簧模型用以表征車輛軌道耦合動力學模型中處于不同狀態的扣件。相較既有研究優化了在扣件扣壓效應模擬方面的建模。

(3)扣件扣壓力失效和完全失效都減弱了扣件對鋼軌的約束性能。扣件失效對輪軌動態行為的影響主要集中在失效側。扣件扣壓力失效對行車安全性無顯著影響，但鋼軌在車輛行經前的上翹位移有所增長；鋼軌加速度也在低頻范圍內增大，主要集中在在8 Hz～50 Hz 中心頻段范圍內，高頻區段區別不大。扣件扣壓力失效對軌道板的振動特性未產生明顯影響。

(4)相較于扣件扣壓力失效模式，完全失效對車軌系統的影響更大，具體表現為各個動力響應指標的顯著增大。車輛進入完全失效區域時，軌下剛度的銳減使得失效側輪軌力出現大幅度減載隨后劇烈波動。根據分析結果可知，鋼軌發生五個扣件完全失效時，輪軌減載率峰值遠遠超過安全限值，已經對行車安全造成了影響，需要引起重視。