教學考試雜志社“優師計劃”階段性成果展示
——高考重難點相關試題選登

1.已知函數f(x)為定義在R上的奇函數,且滿足f(x+2)+f(x)=0,當x∈(0,1]時,f(x)=log2x,則f(log27),f(2 019),f(ln3)的大小關系為

( )

A.f(log27)>f(ln3)>f(2 019)

B.f(ln3)>f(log27)>f(2 019)

C.f(2 019)>f(ln3)>f(log27)

D.f(log27)>f(2 019)>f(ln3)

【答案】A

( )

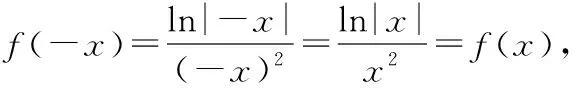
A.[-1,1)∪(1,3]

D.(-∞,-1]∪[3,+∞)

【答案】B

( )

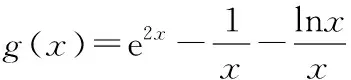
A.1 B.2

C.3 D.4

【答案】B

4.定義在R上的奇函數f(x)的導函數為f′(x),對?x<0,均有xf′(x)-f(x)<0,則不等式(1-2x)f(x)+xf(2x-1)>0的解集為

( )

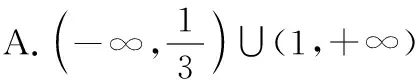
B.(-∞,0)∪(1,+∞)

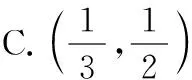
【答案】D

( )

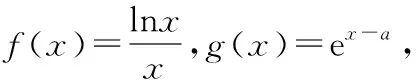
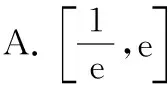
C.[1,e] D.(0,e]

【答案】B

( )

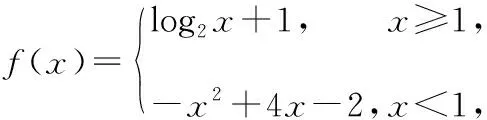
A．(3，+∞) B．(2，+∞)

C．(-∞，3) D．(-∞，2)

【答案】D

【解題分析】因為當x≥1時，f(x)=log2x+1是增函數；當x<1時，f(x)=-x2+4x-2也是增函數，且當x=1時有公共點，所以函數f(x)在R上是增函數.又因為f(1)=1，f(t-1)<1=f(1)，所以t-1<1,即t<2，故選D.

7.若函數f(x)=xlnx-ax2存在極值點，并且所有的極值點都小于2，則實數a的取值范圍為

( )

【答案】B

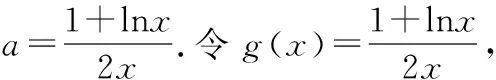
8.已知函數f(x)=ln|x|,若存在實數x使不等式f(x)≥x2-x-2a-2b-ln2成立，則實數a+b的取值范圍為

( )

【答案】C

( )

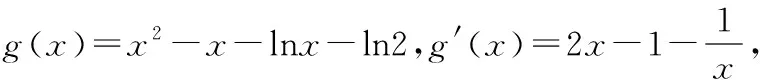
【答案】C

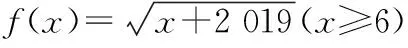
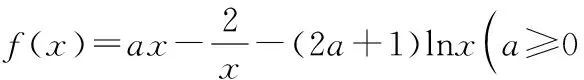
(Ⅰ)試討論函數f(x)的極值的情況；

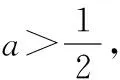
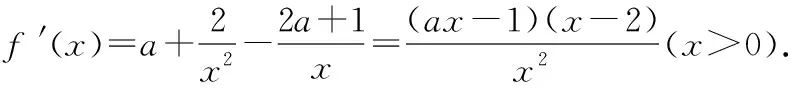
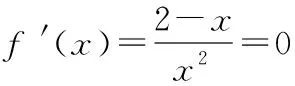
當00,f(x)在(0,2)上是增函數；

當x>2時，f′(x)<0,f(x)在(2,+∞)上是減函數，

∴當x=2時，f(x)有極大值,f(x)無極小值.

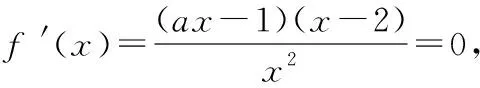
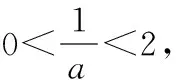
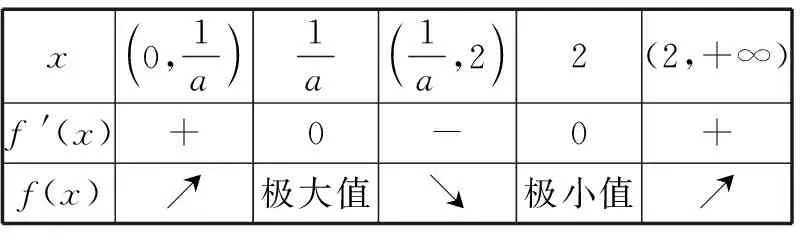
x0,1a 1a1a,2 2(2,+∞)f '(x)+0-0+f(x)↗極大值↘極小值↗

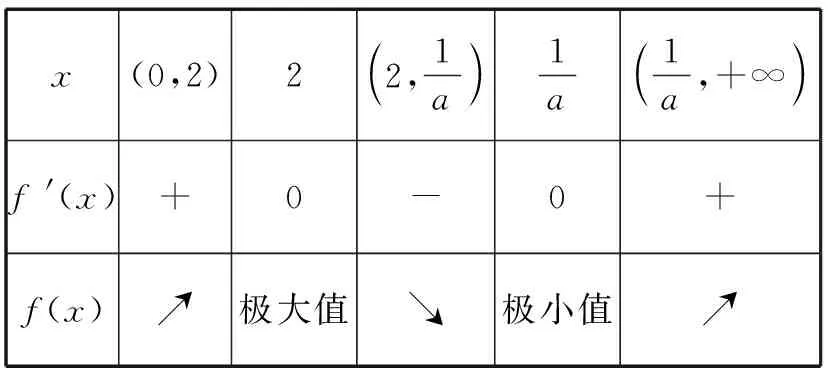
x(0,2)22,1a 1a1a,+∞ f '(x)+0-0+f(x)↗極大值↘極小值↗

綜上所述,當a=0時,當x=2時,f(x)有極大值,f(x)無極小值;

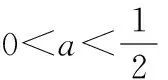
(6分)

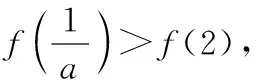
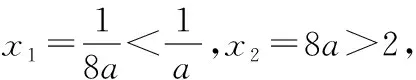
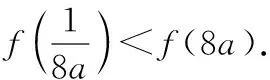
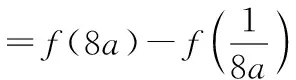
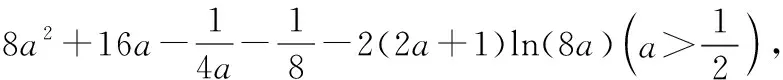
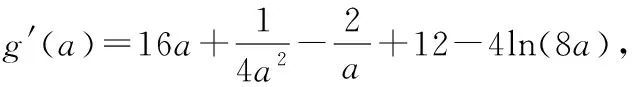
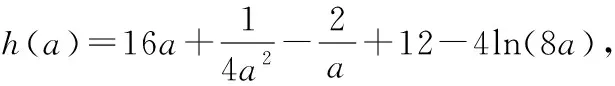
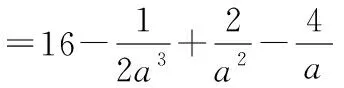
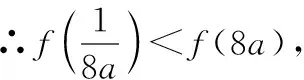
(12分)

11.(本小題滿分12分)已知函數f(x)=ex(1+cosx)+a.

【解題分析】由題意可得f′(x)=ex(1+cosx-sinx).

(Ⅰ)∵當a=0時,f(0)=2,f′(0)=2,

(2分)

∴曲線y=f(x)在點(0,f(0))處的切線方程為 2x-y+2=0.

(5分)

(Ⅱ)令f′(x)=0,則1+cosx-sinx=0,

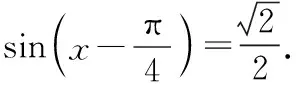
(6分)

(7分)

∴f′(x)>0,

(8分)

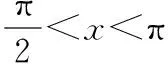
∴f′(x)<0,

(9分)

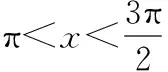
∴f′(x)>0,

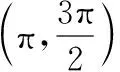
(10分)

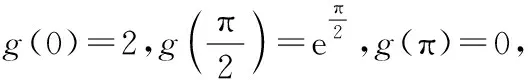
(11分)

(12分)

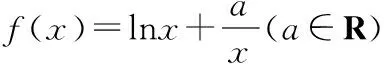
(Ⅰ)求實數a的值，并討論f(x)的單調性;

(Ⅱ)設函數g(x)=ex·f(x)，證明：g(x)>1.

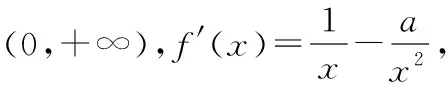
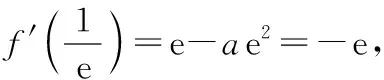
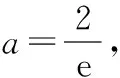
(3分)

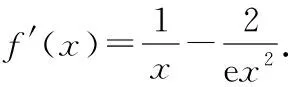
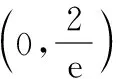
(5分)

(Ⅱ)證明:函數g(x)的定義域為(0,+∞),

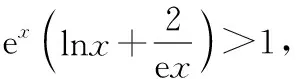
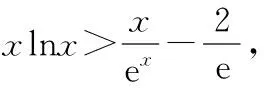
(7分)

設h(x)=xlnx(x>0)，則h′(x)=lnx+1,

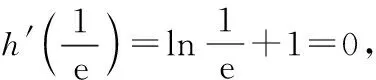
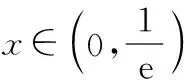
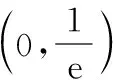
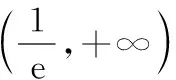
(9分)

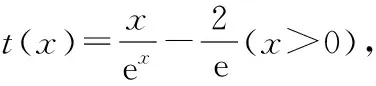
所以當x∈(0,1)時，t′(x)>0，函數t(x)單調遞增,

當x∈(1,+∞)時，t′(x)<0，函數t(x)單調遞減,

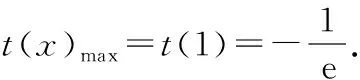
(11分)

綜上，在(0,+∞)上恒有h(x)>t(x)成立，

所以g(x)>1.

(12分)