用數形結合思想求解2019年高考全國卷Ⅱ函數解答題

甘肅 吳天斌

函數解答題往往是高考數學試卷中難度最大的，它不僅運算量大，更突出的是立意新穎，構思精巧，思維容量大，大多數考生想不到、找不到解題的切入點與突破口，而心生畏懼，一籌莫展；數形結合思想往往是解決該類問題的有力杠桿與指路明燈，下面以2019年高考全國卷Ⅱ理科函數解答題為例，例析由數想形、以形助數、由形化數、數形兼備求解函數零點等相關問題中的應用，希望引起更多讀者對數形結合思想的重視與深研.

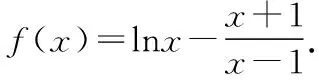
(Ⅰ)討論f(x)的單調性，并證明f(x)有且僅有兩個零點；

(Ⅱ)設x0是f(x)的一個零點，證明曲線y=lnx在點A(x0,lnx0)處的切線也是曲線y=ex的切線.

分析：(Ⅰ)思路①(直接判斷法)：先對函數f(x)求導，結合定義域，判斷函數的單調性，畫出函數f(x)圖象草圖，取一些特殊函數值，然后結合零點存在定理證明函數f(x)有且僅有兩個零點；

思路②(極限、極值、最值分析法)：先對函數f(x)求導，結合定義域，判斷函數的單調性，畫出函數f(x)圖象草圖，求端點極限值或極值或最值，比較它們與0的大小關系，再結合零點存在定理證明函數f(x)有且僅有兩個零點；

思路③(函數分離法)：先對函數f(x)求導，結合定義域，判斷函數的單調性，然后令f(x)=0，將所給函數分離成兩個熟悉的函數，兩個新函數的交點個數即為原函數的零點個數.

(Ⅱ)思路①：先求出曲線y=lnx在點A(x0,lnx0)處的切線l，然后求出當曲線y=ex的切線l′的斜率與l的斜率相等時，再證明曲線y=ex的切線l′在縱軸上的截距與l在縱軸的截距相等即可；

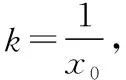
解析：(Ⅰ)解法1：

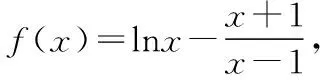
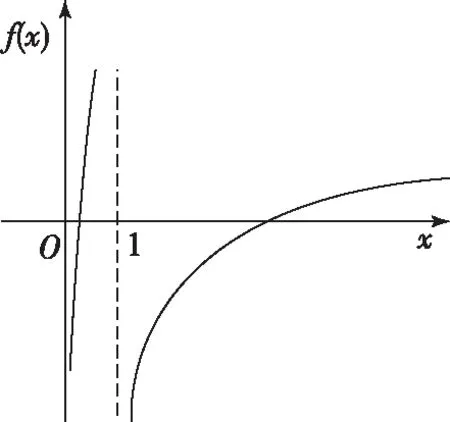
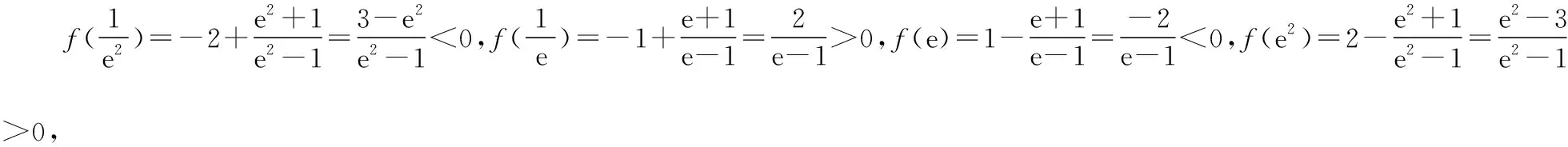
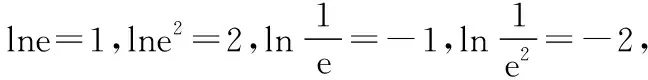
解法2：

函數f(x)的單調性及草圖同解法1所示；

①x∈(0,1),當x→0-時y→-∞，而x→1-時y→+∞，由f(x)單調性和零點存在定理知當x∈(0,1)，函數f(x)有唯一的零點；

②x∈(1,+∞)，當x→1+時y→-∞，當x→+∞時y→+∞，由f(x)單調性和零點存在定理知當x∈(1,+∞)，函數f(x)有唯一的零點；所以函數f(x)在定義域(0,1)∪(1,+∞)內有且僅有兩個零點；

點評：x→0+指的是變量x從0的右側趨向于0，x→1+指的是變量x從1的右側趨向于1，其余類似，這種做法是把解法1推向于極限情形，更直接地解決問題，只不過對考生的知識、能力要求更高.

解法3：

函數f(x)的單調性同解法1，草圖如圖所示；

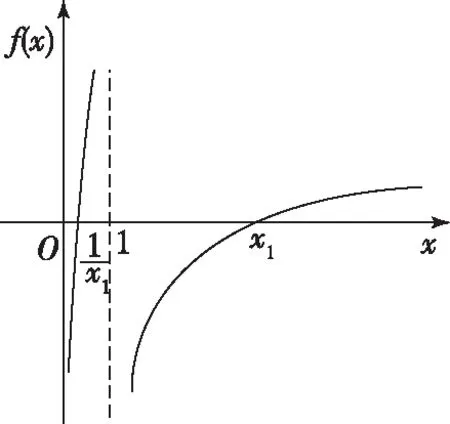
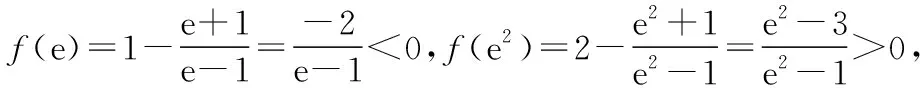
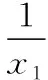
解法4：

函數f(x)的單調性同解法1；

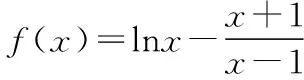
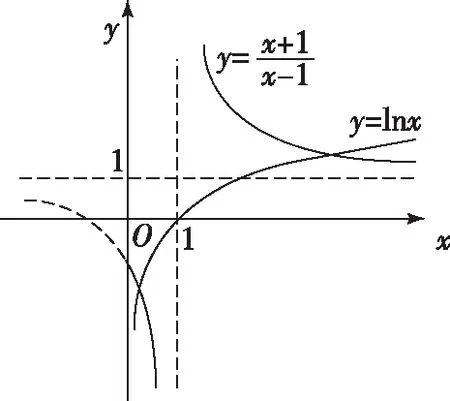
點評：數形結合思想的本質是轉化，由函數零點轉化為兩個我們最為熟悉的函數圖象的交點，把復雜問題轉化為較容易的問題，是數形結合思想的靈魂和精神所在；有時候，一個圖形勝過千言萬語，把數學的簡潔美、直觀美、形象美體現得淋漓盡致，這不但能起到簡化運算，降低試題難度的作用，而且還能激發學生學習數學的興趣.

(Ⅱ)解法1：

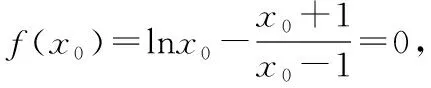
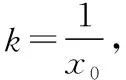
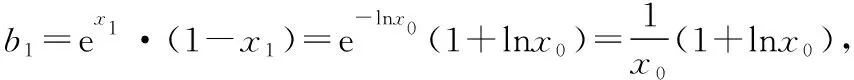
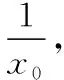
解法2：

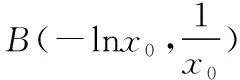
在面對“山重水復疑無路”的解題困境時，數形結合思想往往是“柳暗花明又一村”的有效途徑，所以我們要一邊演算、一邊思考、一邊修正草圖，畫出與之匹配的圖形，通過數與形的結合，將抽象問題具體化、復雜問題簡單化、陌生問題熟悉化，這不僅有利于學生快速地找到解決問題的切入點、突破點，摸索解題思路，弄清問題實質，而且有助于減輕學生對函數解答題的恐懼心理，指引學生順利求解，成功登頂.