探究數形結合在高考數學函數解答題中的應用

甘肅 王新宏

我國著名數學家華羅庚曾作詩形容數形結合的思想方法：“數缺形時少直觀，形缺數時難入微，數形結合百般好，數形分離萬事休.”函數解析式與其圖象建立了一一對應關系，使得數與形的研究可以相互轉化，高考命題者將充分利用函數解答題的這一特點，考查考生能否將復雜的函數問題轉化為借助直觀的幾何圖形來解決問題的能力.

【例1】(2019·全國卷Ⅲ理·20)已知函數f(x)=2x3-ax2+b.

(1)討論f(x)的單調性；

(2)是否存在a,b，使得f(x)在區間[0,1]上的最小值為-1且最大值為1？若存在，求出a,b的所有值；若不存在，說明理由.

【分析】(1)求出f′(x)=0的兩根，比較兩個的大小，結合f′(x)的圖象草圖，分情況討論函數f(x)的單調性；(2)根據f′(x)與f(x)的圖象草圖，利用函數f(x)在x∈[0,1]的單調性，進行最大值和最小值的判斷，最終得出a,b的值.

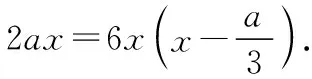
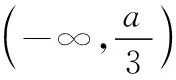
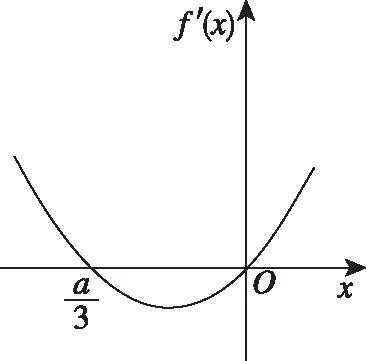
圖1

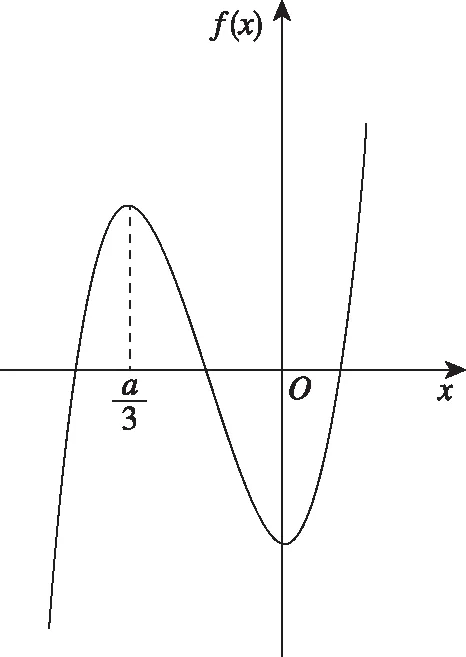
圖2

②當a=0時，函數f′(x)的圖象草圖如圖3所示，函數f(x)在(-∞,+∞)上單調遞增；

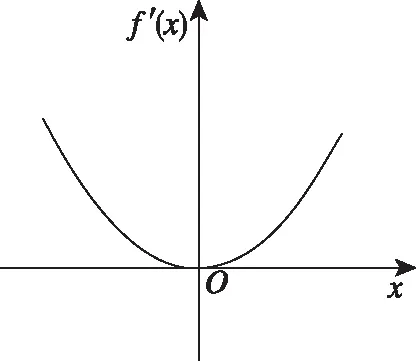
圖3

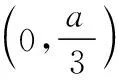
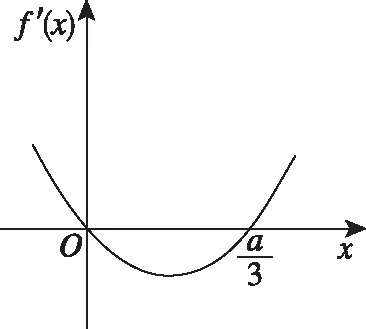
圖4

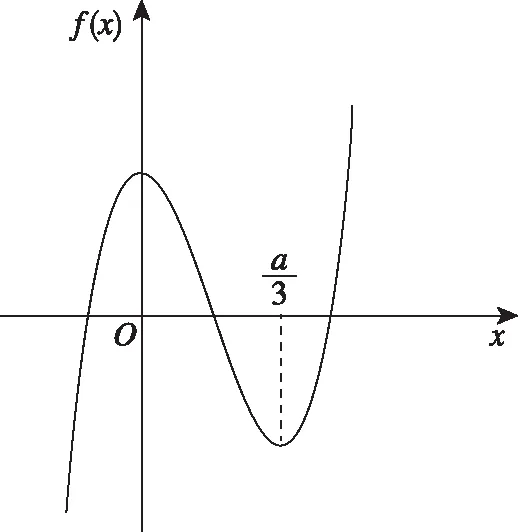
圖5

(2)存在a,b,使得函數f(x)在區間[0,1]上有最大值1和最小值-1.

①若a<0，函數f(x)的圖象草圖如圖2所示，此時函數f(x)在區間[0,1]上單調遞增，所以f(0)=-1，f(1)=1代入解得b=-1，a=0，與a<0矛盾，所以a<0不成立；

②若a=0，函數f(x)在(-∞,+∞)上單調遞增；所以f(0)=-1，f(1)=1，代入解得a=0，b=-1，符合要求；

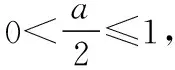
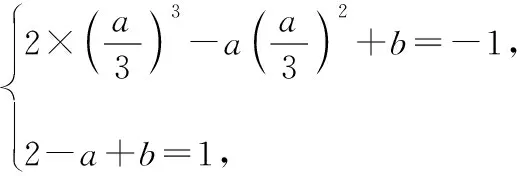
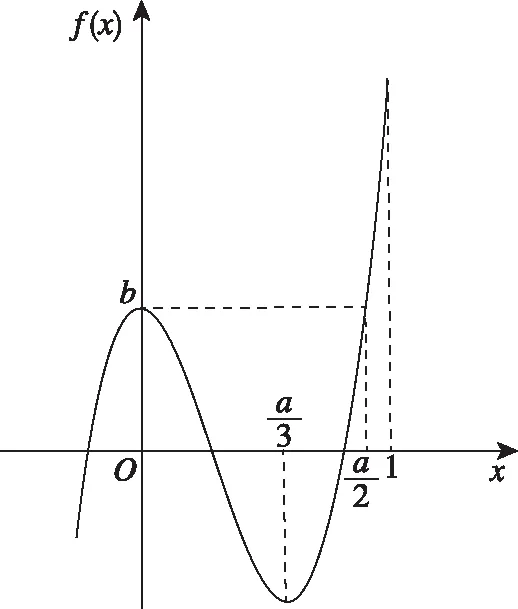
圖6

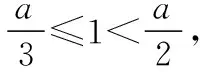
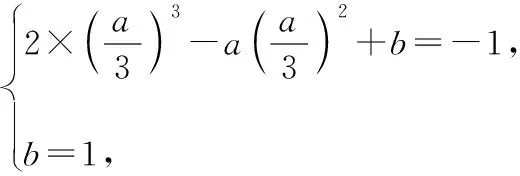
圖7

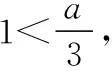
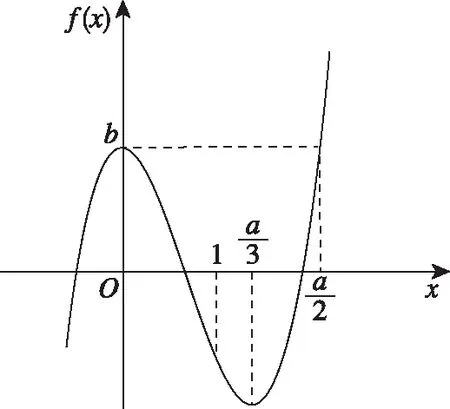
圖8

②做函數解答題時，一邊做題，一邊思考圖形，畫出與之匹配的圖形，通過圖形，看透問題實質，指引著我們解題的方向，事半功倍，所以數形結合百般好，以形助數效率高.

【例2】(2019·全國卷Ⅰ理·20)已知函數f(x)=sinx-ln(1+x)，f′(x)為f(x)的導數.證明：

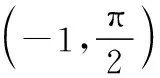
(2)f(x)有且僅有2個零點.

【分析】(1)寫出f′(x)的表達式，利用其導函數f″(x)來研究f′(x)的單調性與極值點.

(2)以x為主元進行分類討論，分別在各個區間上，由導函數的單調性以及特殊點的f′(x)的值來判斷f′(x)與0的關系，得到f(x)的單調性，從而得到在各個區間的零點個數.

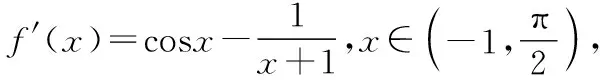
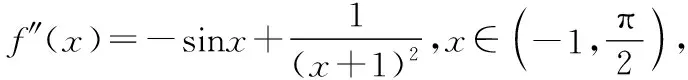
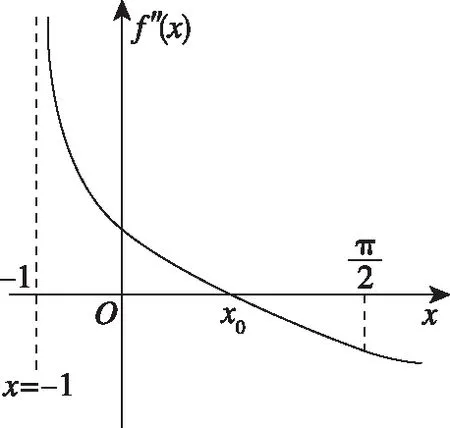
圖9

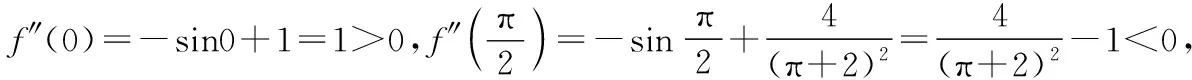
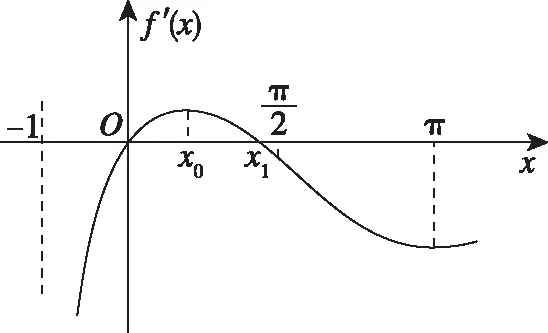
圖10

【點評】含有對數函數、指數函數、三角函數與多項式函數的方程稱為超越方程，超越方程我們是沒有辦法求解的，但高考函數解答題中f′(x)=0(或f″(x0)=0)的方程往往都是超越方程，此時我們常用的策略有兩種：

①二次求導，即對y=f′(x)函數再次求導，二階導函數y=f″(x)的正負對應著y=f′(x)的增減性，進而得出導函數y=f′(x)的正負情況，最終確定原函數y=f(x)的增減情況；

②設而不求，即先分析導函數(或二階導函數)的單調性，判斷它是否存在零點，若存在，再結合零點存在定理判斷零點的個數，進而設出零點，對問題進行求解.

①當x∈(-1,0]時，由草圖10可知f′(x)在(-1,0]上單調遞增，所以f′(x)≤f′(0)=0即f(x)在(-1,0]上單調遞減,又f(0)=0，所以x=0為函數f(x)在(-1,0]上的唯一零點；

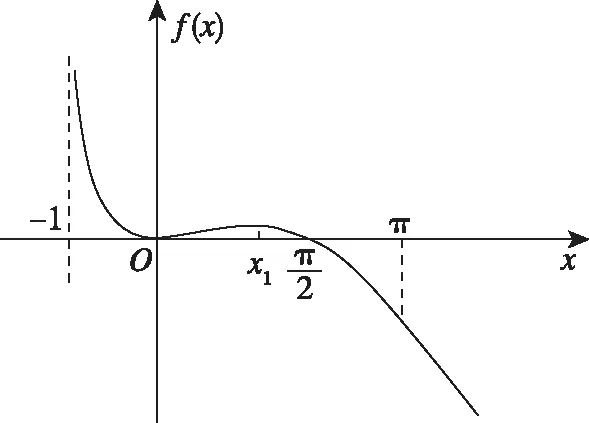
圖11

④當x∈(π,+∞)時，函數f(x)的圖象草圖如圖11所示，sinx∈[-1,1]，ln(x+1)>ln(π+1)>lne=1，所以sinx-ln(x+1)<0，即f(x)在(π,+∞)上不存在零點.

綜上所述，f(x)有且僅有2個零點.

【點評】數形結合可以很好地為解題探究思路，但不能用形的直觀代替相關的計算與推理，畫圖不能太草，要盡可能準確，要善于用單調性、特殊點、特殊的數來準確定位圖形的位置關系，幫助我們順利解題.

數形結合是求解數學問題重要的思想方法，使用這種方法，很多問題迎刃而解，且解法簡捷，特別是在函數解答題中發揮著巨大的作用，在求解過程中，圖形可幫助我們找到解決問題的突破口，指引我們解題的方向，通過數與形的結合，會使復雜問題直觀化、簡單化，使解題的過程順暢自然，水到渠成.