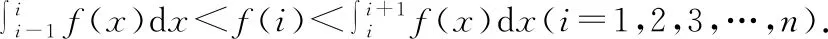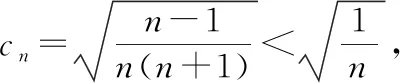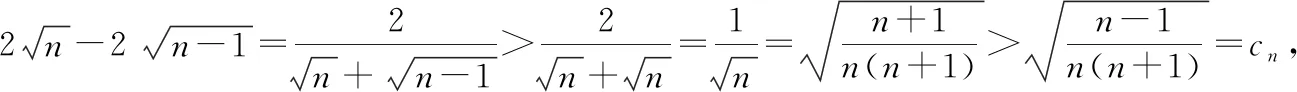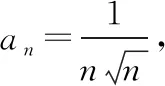數列不等式證明的解題策略
福建 黃清波
常見的數列不等式證明大多與數列求和或求積有關,這類題型一直是各類考試的熱點,也是學生學習的難點.證明的過程中經常要用到放縮法或數學歸納法等難度較大的數學方法,需要學生有敏銳的數學觀察力和熟練的轉化能力,同時還要能夠恰當的放縮,解題過程技巧性強且難以操控,對學生知識以及思維能力要求較高.本文以2019年高考數學浙江卷第20題為例,從多個視角去考量這類問題的求解策略,希望讀者能夠從中受到啟發,選擇適當的方法解決問題.
題目:設等差數列{an}的前n項和為Sn,a3=4,a4=S3.數列{bn}滿足:對每個n∈N*,Sn+bn,Sn+1+bn,Sn+2+bn成等比數列.
(Ⅰ)求數列{an},{bn}的通項公式;
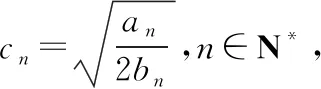
【分析】本題主要考查等差數列、等比數列、數列求和、不等式的證明等基礎知識,考查推理論證能力、運算求解能力和綜合運用能力,考查邏輯推理、數學運算等核心素養,難度較大.
策略一:數學歸納法
【分析】由于數列不等式與自然數有關,可優先考慮用數學歸納法.第一步,先驗證n=1時,不等式成立;第二步,假設n=k(k∈N*)時不等式成立,充分利用假設,恰當放縮,證明n=k+1時不等式也成立.即證原不等式成立.
解法1:(Ⅰ)由已知條件易求得an=2n-2,n∈N*,bn=n2+n,n∈N*.
我們用數學歸納法證明.
(1)當n=1時,c1=0<2,不等式成立;
(2)假設n=k(k∈N*)時不等式成立,
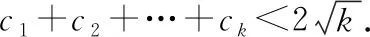
那么,當n=k+1時,
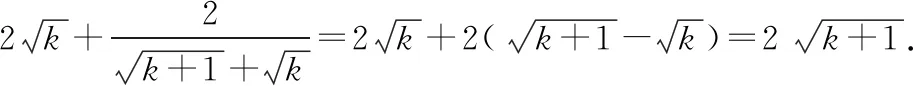
即當n=k+1時不等式也成立.
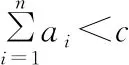
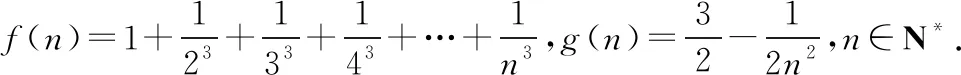
(Ⅰ)當n=1,2,3時,試比較f(n)與g(n)的大小關系;
(Ⅱ)猜想f(n)與g(n)的大小關系,并給出證明 .
解:(Ⅰ)當n=1時,f(1)=1,g(1)=1,所以f(1)=g(1);
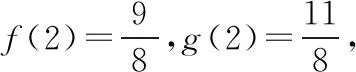

(Ⅱ)由(Ⅰ)猜想f(n)≤g(n),下面用數學歸納法證明.
(1)當n=1,2,3時,不等式顯然成立;
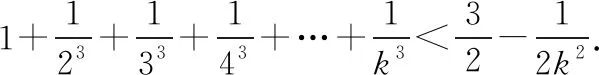

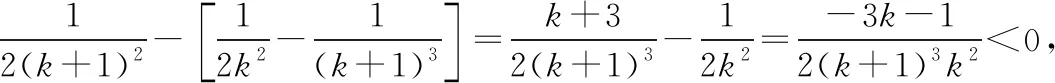

根據(1)和(2)可知,對任意n∈N*,都有f(n)≤g(n)成立.
策略二:分項比較法


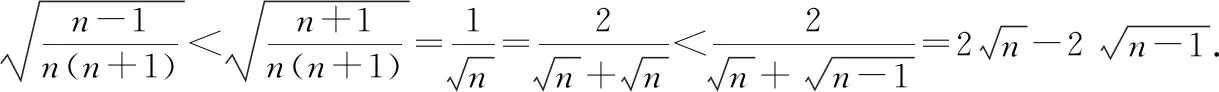

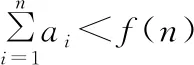
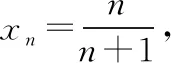
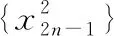
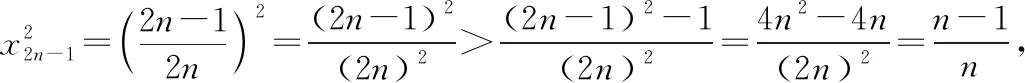
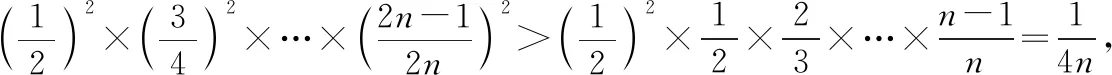

策略三:定積分法
【分析】求曲邊梯形的面積是采用分割、近似代替、求和、取極限的方法,并由此抽象出定積分的概念,關鍵步驟是以小曲邊梯形的面積近似值作為數列的項,再數列求和,把定積分與數列聯系起來.