非齊次非對稱Keyfitz-Kranzer 氣體方程組的Riemann 問題
李舒琪
(新疆大學數學與系統科學學院,新疆烏魯木齊830046)
非齊次Chaplygin 氣體非對稱Keyfitz -Kranzer方程組為[1]
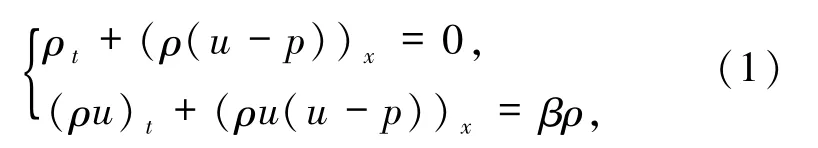
其中ρ、u、p 分別表示氣體密度、速度和壓強.狀態方程是方程組(1)的 Riemann 初值為
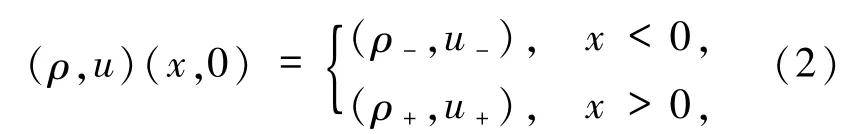
其中 ρ±和 u±是給定的常數.
非線性雙曲型守恒律方程組在現代數學中是一個非常重要的研究方向,并且在空氣動力學、等離子動力學、氣象學、經典相對論流體力學等學科都有著極其廣泛的應用[2].尤其是起源于非線性雙曲型守恒律方程組的激波解、疏散波解和接觸間斷解的研究都有著理論意義和實際參考價值,同時也可以用來研究 Aw - Rascle 交通流[3].非對稱 Keyfitz -Kranzer方程組屬于非線性雙曲型守恒律方程組的類型,因此受到許多學者的關注[4-7].
當 β =0 時,方程組(1)為齊次非對稱 Keyfitz-Kranzer方程組,具有線性退化的特性,這個問題引起了許多學者的研究興趣.2013 年,Lu[4]研究了非對稱Keyfitz - Kranzer 方程組全局熵解的存在性,Cheng[5]研究了非對稱 Keyfitz -Kranzer 方程組線性衰減守恒律的Riemann 問題和基本波的相互作用. 2014 年,Guo 等[6]研究了多方氣體和廣義Chaplygin氣體非對稱Keyfitz-Kranzer方程組壓力消失極限問題. 2018 年,李舒琪[7]研究了非對稱Keyfitz-Kranzer方程組波的相互作用.
非齊次Chaplygin氣體非對稱Keyfitz -Kranzer方程組(1)可以簡單描述Chaplygin 氣體和黑物質的相互作用[2]的Riemann問題,因此其Riemann問題的研究一直是一個熱門課題.但是由于其自身非齊次性的解析難度,使得目前對于非齊次Chaplygin氣體非對稱Keyfitz - Kranzer 方程組的研究很少.2012 年,Gu 等[8]研究了非齊次非對稱 Keyfitz -Kranzer方程組的全局弱解的有界性. 2017 年,Li等[9]利用分離的 δ 函數法研究了非齊次非對稱Keyfitz-Kranzer方程組中δ 激波的交互性,同年研究了非齊次非對稱Keyfitz -Kranzer 方程組在不同δ 初值下的 Riemann 問題[10].
本文在前人的基礎上繼續研究非齊次非對稱Keyfitz-Kranzer方程組的Riemann 問題.首先引入一個新的變量把非齊次非對稱Keyfitz -Kranzer 方程組轉化為守恒形式,并得到Riemann 解的整體結構,與齊次非對稱Keyfitz - Kranzer 方程組的Riemann解不同的是非齊次非對稱Keyfitz-Kranzer方程組的Riemann解是非自相似的.由特征分析法和相平面分析法,可以得到δ激波會在某些特定情況下出現在Riemann 解中,再通過廣義的Rankine -Hugoniot條件得到了 δ 激波的位置、傳播速度和強度.
1 修正守恒方程的Riemann問題
這部分主要研究 Keyfitz -Kranzer 方程組(1)守恒形式的Riemann問題,引入新的變量v(x,t)=u(x,t)- βt,則方程組(1)可以寫成如下守恒形式:
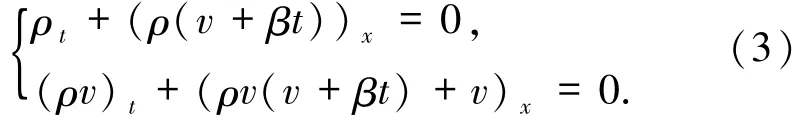
其Riemann初值為
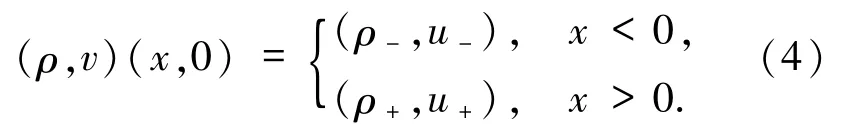
方程組(3)可寫為
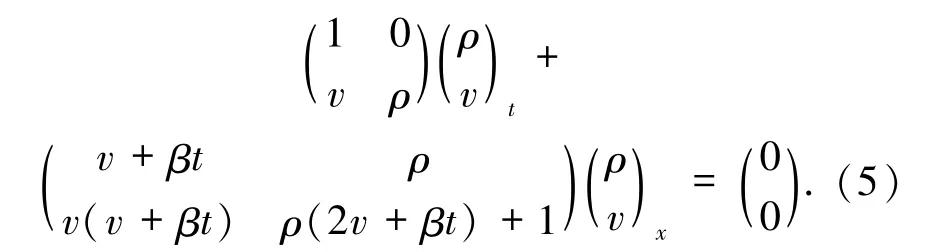
由上式,方程組(3)有2 個特征根
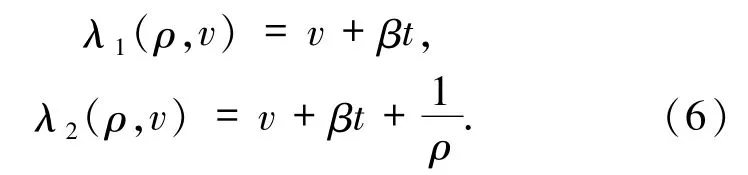
對應的右特征向量分別為
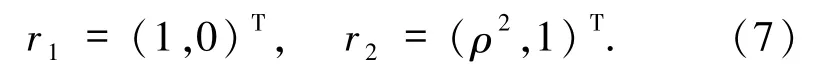
通過計算可知▽λi·ri=0(i =1,2),這里▽表示(ρ,v)的梯度,因此特征域 λ1和 λ2是線性退化的,會產生接觸間斷,用J表示.
x = x(t)處的有界間斷用 σ(t)= x′(t)表示,則方程組(3)的Rankine-Hugoniot條件:
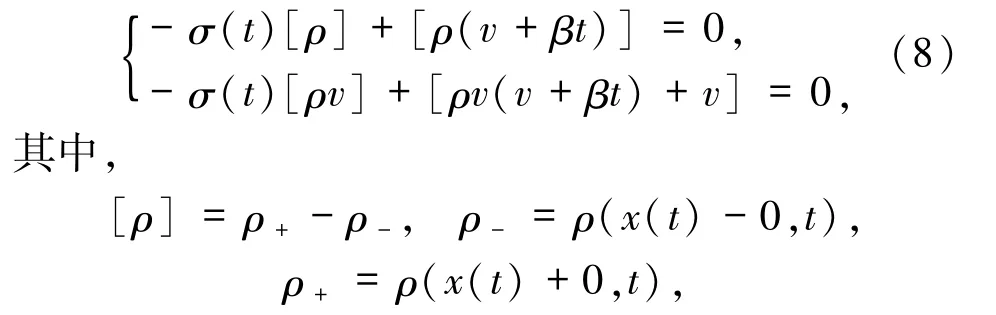
[ρ]表示ρ的跳躍,很明顯間斷的傳播速度依賴于參數t,這與齊次方程組有所不同.
若 σ(t)≠0,由(8)式得到
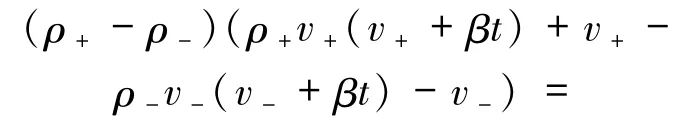

因此2 個非空狀態(ρ-,v-)和(ρ+,v+)可通過 1-接觸間斷J1連接當且僅當
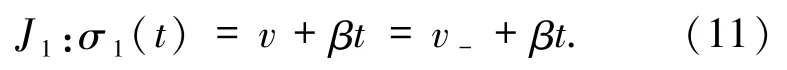
也可通過2 -接觸間斷J2連接當且僅當
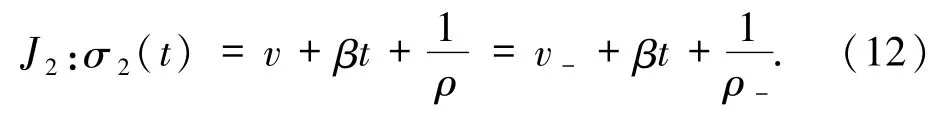
在(ρ,v)平面,若給定左狀態(ρ-,u-),從(11)式可知1 -接觸間斷 J1(ρ-,u-)滿足 v =u-,從(12)式可知 2 - 接觸間斷 J2(ρ-,u-)滿足和 ρ =0 為漸近線.此外,過點可以畫曲線 S 滿足(12)式,即事實上,在(ρ,v)平面,曲線 S 是由曲線J2(ρ-,u-)向左平移個單位得到,簡而言之,(ρ,v)平面被分成 2 個區域Ⅰ(u-,ρ-),Ⅱ(u-,ρ-)(見圖1).

圖 1 守恒律方程組(3)的(v,ρ)相平面Fig. 1 Phase plane (v,ρ)of conservation system (3)
若(ρ+,u+)∈Ⅰ,即滿足則方程組(3)的 Riemann 解由 J1、J2及兩者之間的非真空常狀態(ρ*,v*)組成,中間狀態(ρ*,v*)滿足
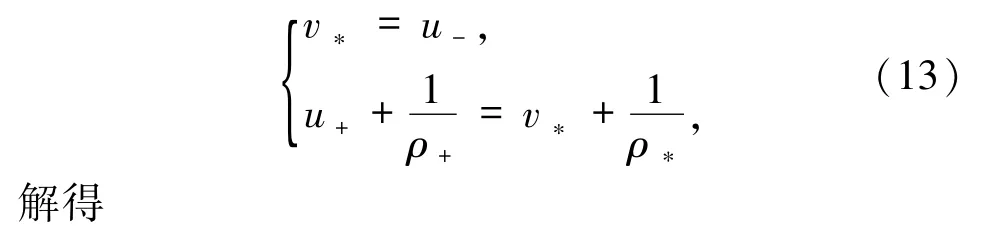
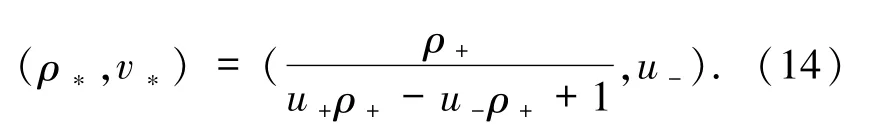
J1、J2的傳播速度分別為
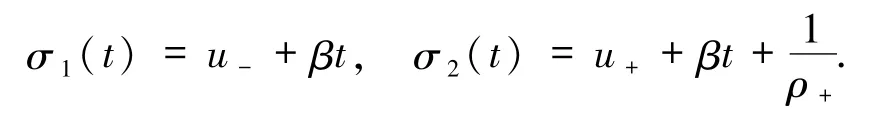
當(ρ+,v+)∈Ⅱ,即則 Riemann 問題(3)和(4)的特征曲線在區域 Ω 重疊,使得在區域Ω內出現了奇異點.簡單起見,只計算從原點(0,0)出發的特征曲線,它可以由下式決定:
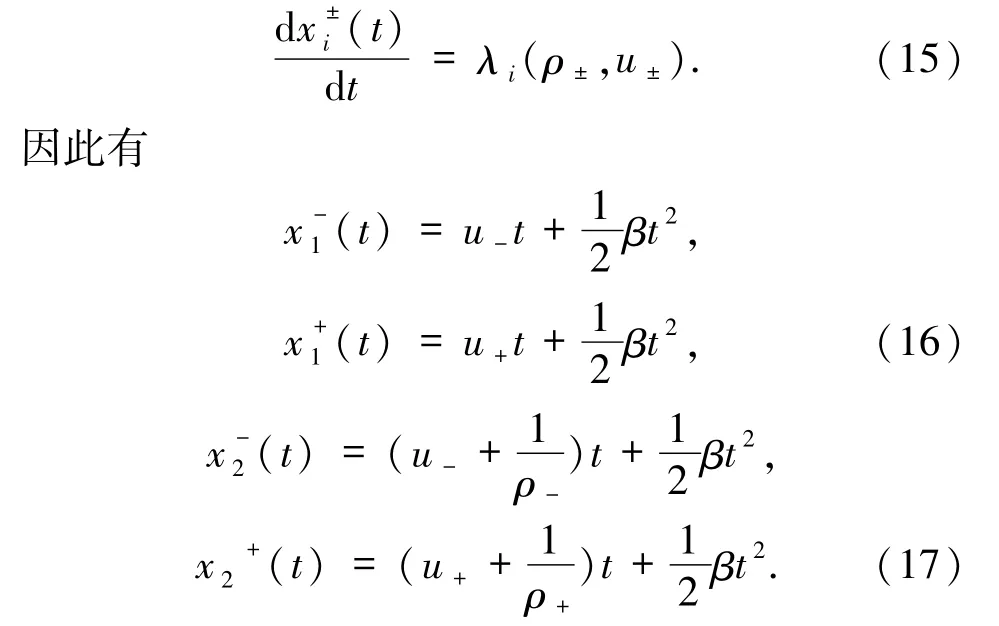
這種情形的解可以通過圖2 來說明.
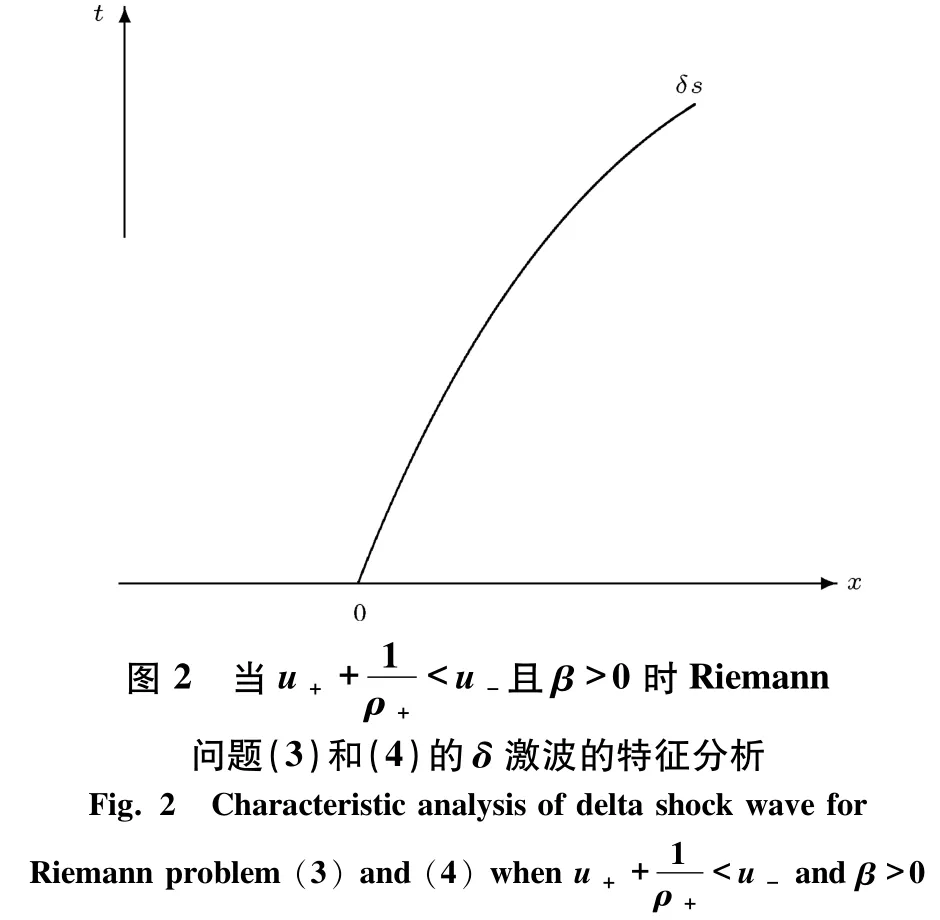
線性退化特征值的疊加造成Riemann問題(3)和(4)解的奇異性.因此,在某些特定情況下,Cauchy問題不存在弱的L∞解時,非經典解就會出現.為了求解非經典解的 Riemann 問題(3)和(4),引入了δ激波測度定義.
定義 1.1定義一個在光滑曲線 S = {(x(s),t(s)):a < s < b}上的二維的加權 δ 激波測度 p(s)δS為
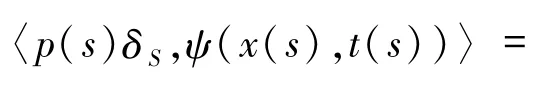
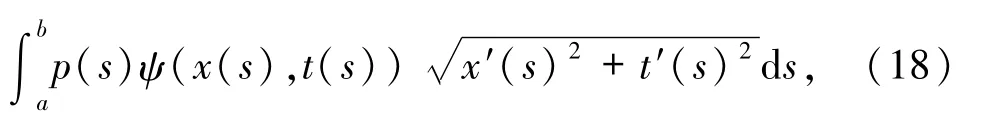
為了方便,選取參數s =t且用
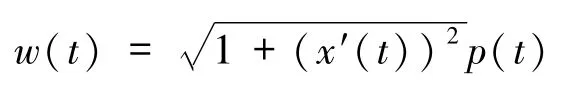
來表示δ激波的權.
設 Γ{γi|i∈I}是一個上半平面{(x,t)|x∈R,t∈(0,+∞)}包含光滑曲線 γi的集合,其中,i∈I,I是指標集.I0= {γj|j∈I},γj是初始點在 x 軸上的曲線表示 γj的初始點集.那么定義方程組(3)在 δ 激波測度初值的 Cauchy 問題的解.
定義1.2令(ρ,v)是一個分布函數對,ρ可表示為

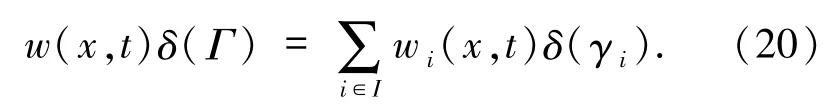
δ激波的初值為
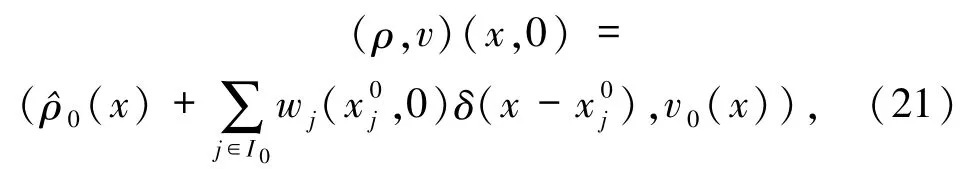
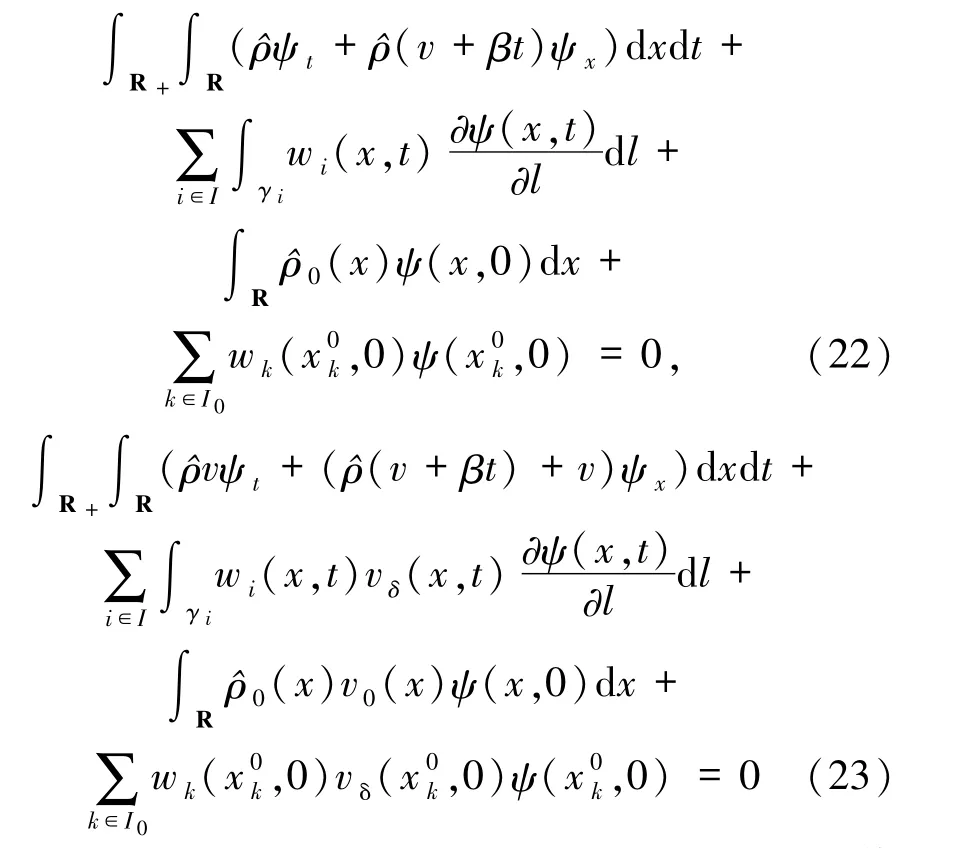
成立,則分布函數對(ρ,v)為方程組(3)在初值(21)式的 δ激波解,其中是函數 ψ 在圖 γi上的方向導數表示沿著弧γi進行線積分.
當(ρ+,v+)∈Ⅱ,即考慮 Riemann問題(3)和(4)的一個分片光滑解,其形式為
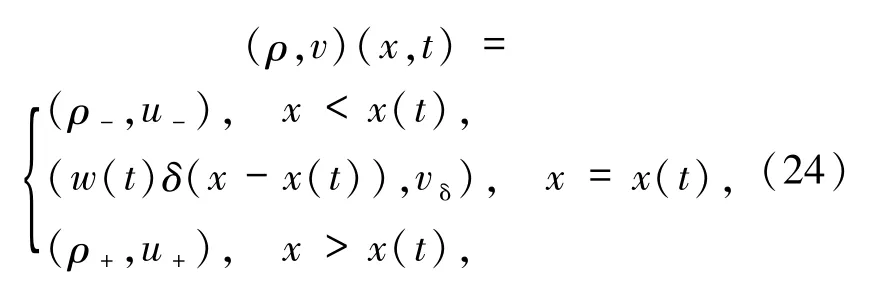
其中,x = x(t)表示 δ 激波曲線,w(t)和 σ(t)=x′(t)表示 δ激波的強度和傳播速度,vδ是 v 在 δ 激波曲線上的分布在這條δ激波曲線上是0.
Riemann 問題(3)和(4)的 δ 激波解(24)需要滿足如下廣義的Rankine-Hugoniot條件
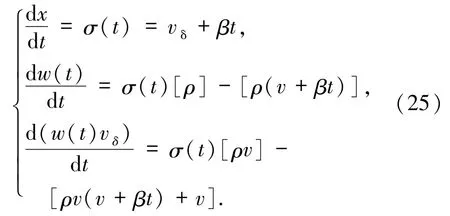
假定 δ激波曲線 Γ:{(x,t)|x = x(t)}是(x,t)平面上一條過間斷點(ρ,v)的光滑曲線.令 P 是 Γ 上的任意一點,Ω 是以點P 為中心的一個小球.假設Ω和 Γ 的交點是 P1= (x(t1),t1)和 P2= (x(t2),t2),t1< t2,并且 Ω-和 Ω+分別表示 Ω 被 Γ 截斷的左半部分和右半部分.對于任意的檢驗函數來說有
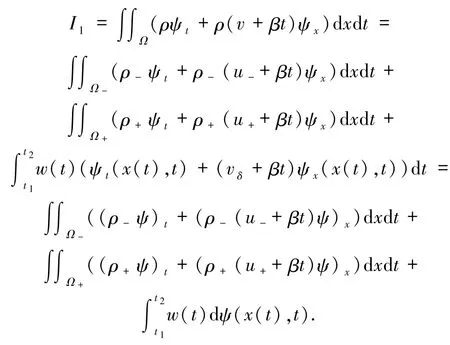
利用散度定理得
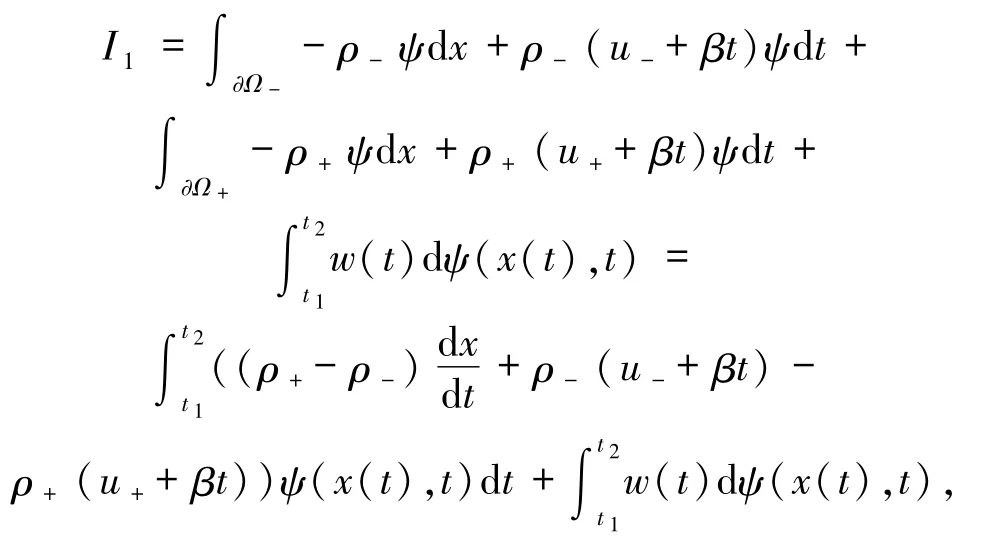
其中 ?Ω±是 Ω±的邊界.因此對于任意 ψ(x,t)∈當 I =0 時,(25)式的第 2 個等式成立.同1理可得
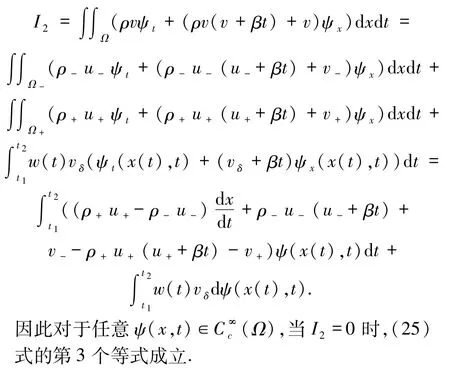
為了確保解的唯一性,還應成立如下δ 激波的廣義熵條件
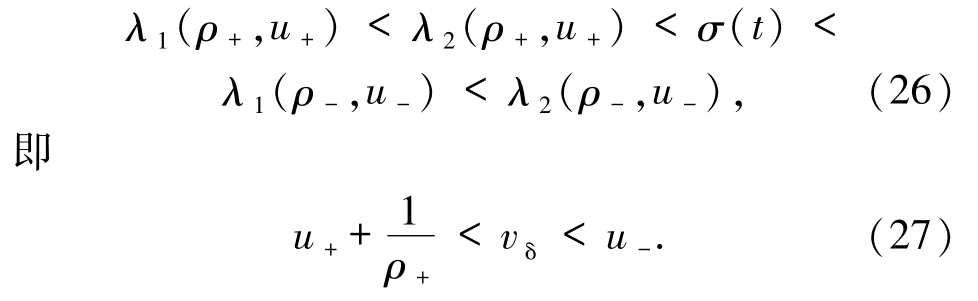
廣義的 Rankine-Hugoniot條件(25)反映了 δ 激波的位置、強度和傳播速度的關系. δ 激波的熵條件(26)反映了間斷兩邊的特征線是進入的.
由(25)式得


當 ρ-= ρ+,可得

2 方程組(1)的Riemann問題
本節研究方程組(1)和(2)的 Riemann 問題.當(ρ+,u+)∈Ⅰ,即那么(1)和(2)式的Riemann解如下(見圖3).
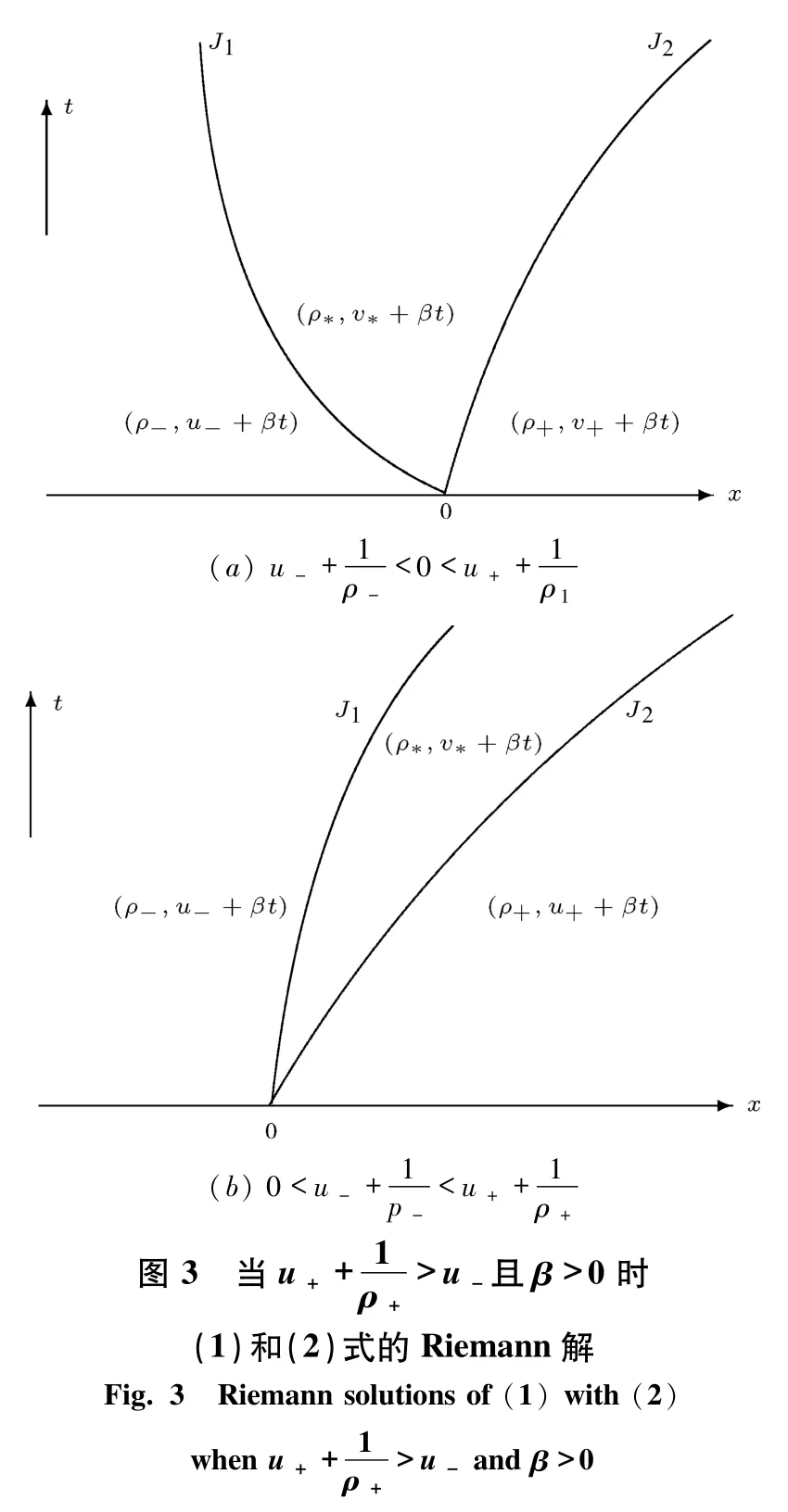
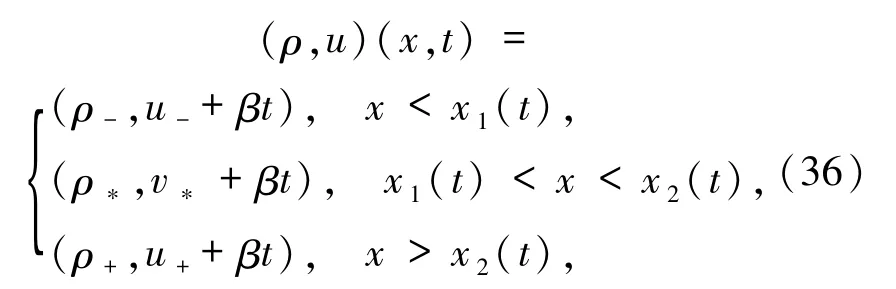
其中(ρ*,v*)由(14)式給出,接觸間斷 J1和 J2由下式決定
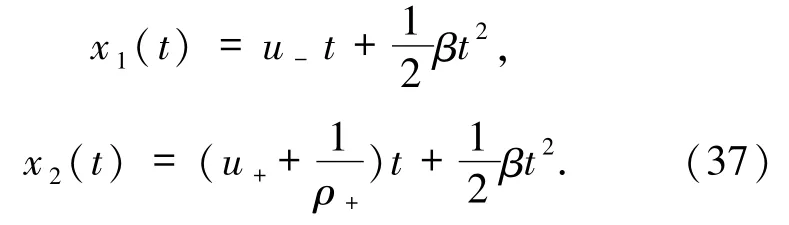
同理,當(ρ+,u+)∈Ⅱ時,即定義Riemann問題(1)和(2)分布意義下的弱解.
定義2.1方程組(1)的δ激波型初值為
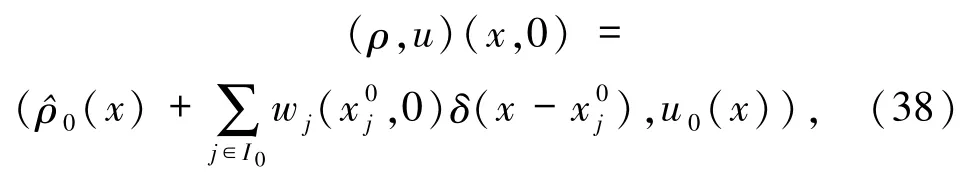
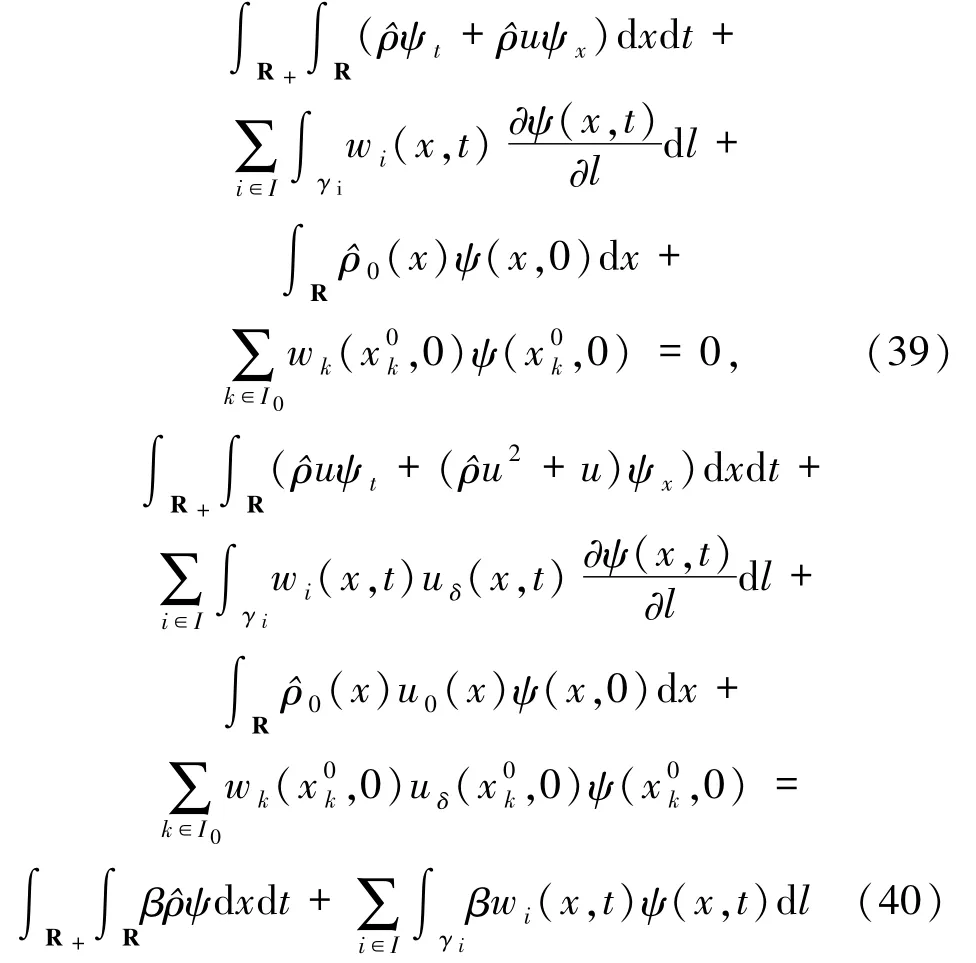
都成立,則分布函數對(ρ,u)為方程組(1)在初值(38)的 δ激波解.

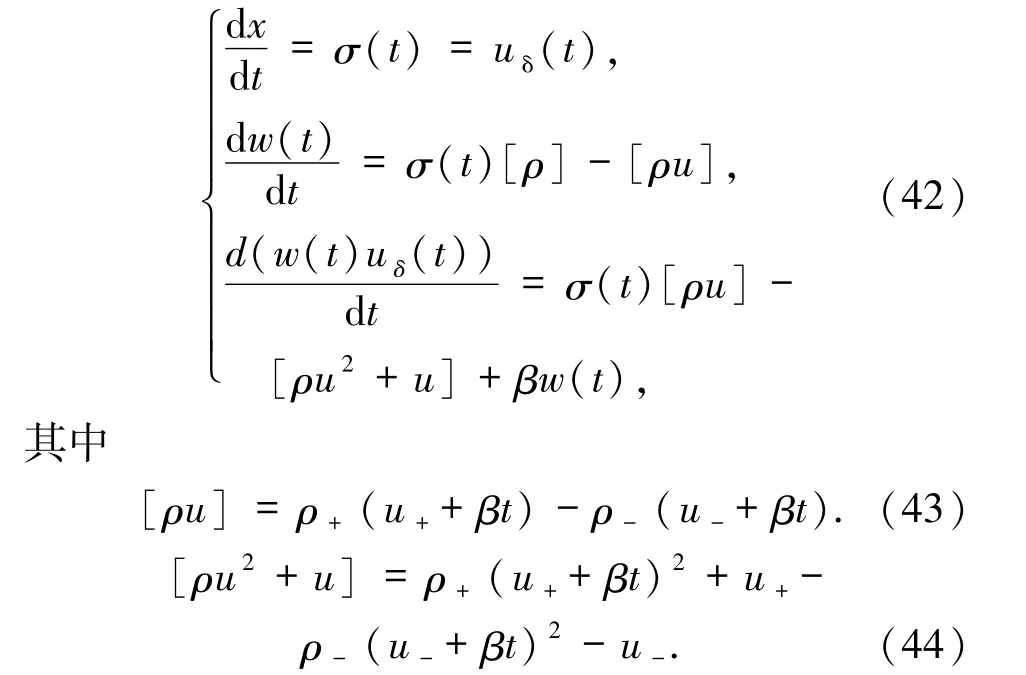
為了確保(1)和(2)式的 Riemann 問題解的唯一性,當時,得到δ激波的廣義熵條件
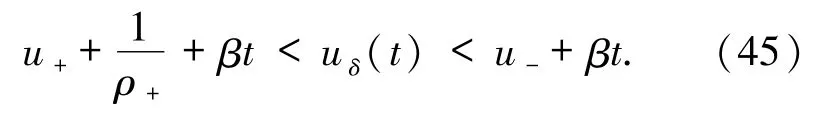
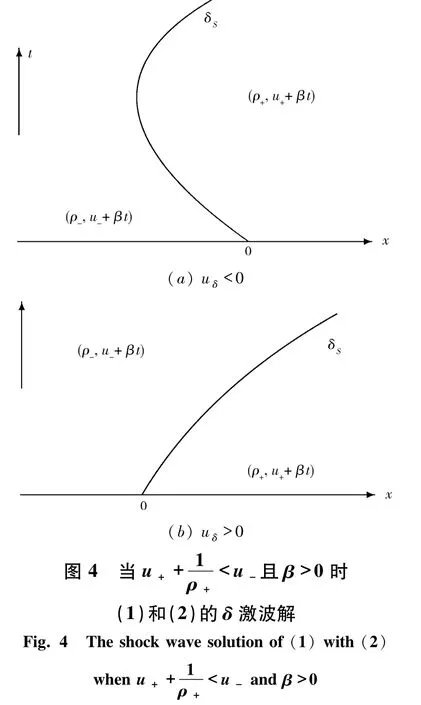
與前面的推導相同,由(42)和(45)式得到x(t)、σ(t)和 w(t).一般來說,當 Riemann 初值(2)滿足且 ρ ≠ρ 時,(1)和(2)式的-+Riemann解可以用如下定理來說明.
定理2.1當 Riemann 初值滿足u-且 ρ-≠ρ+,那么 Riemann 問題(1)和(2)的 δ激波解為
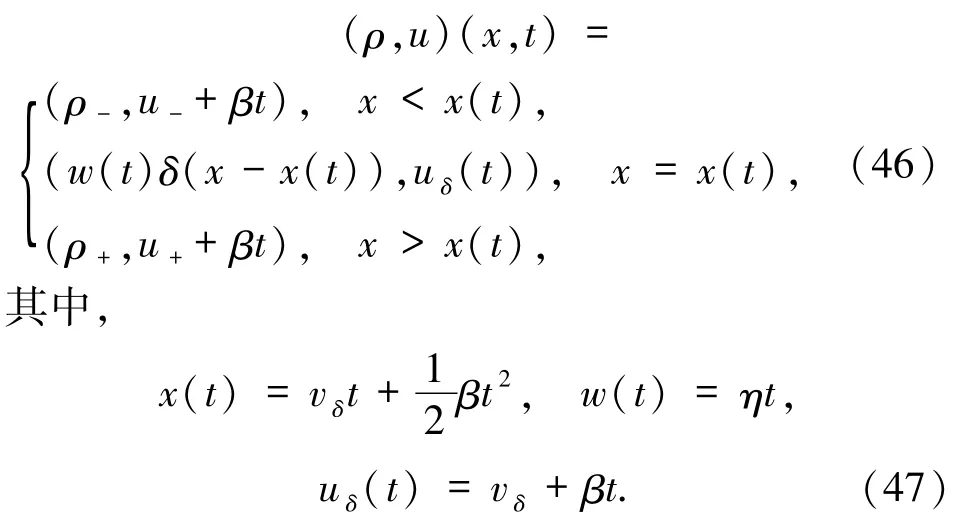
這里 η 和 vδ分別由(31)和(32)式給出.
證明當時,Riemann 問題(1)和(2)的解是 δ激波.由(43)式得(42)式的第 2 個方程可以寫為
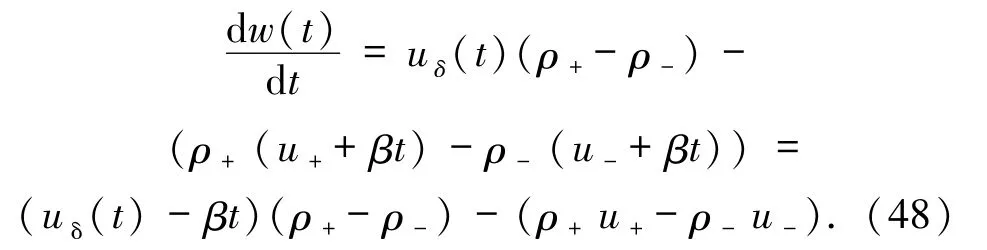
由于 uδ(t)-βt是常數,(42)式的第三個等式可以重寫為
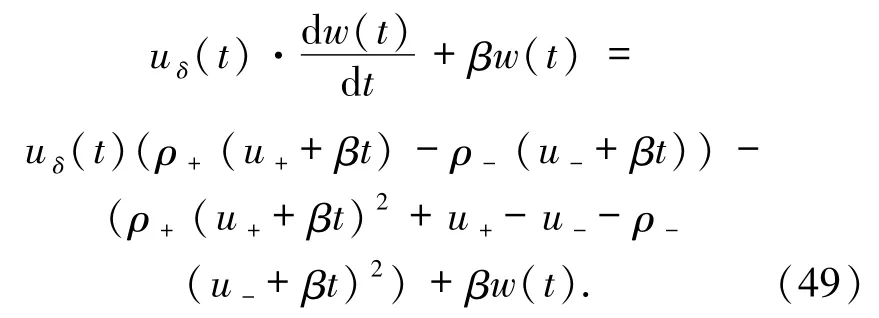
化簡(49)式得
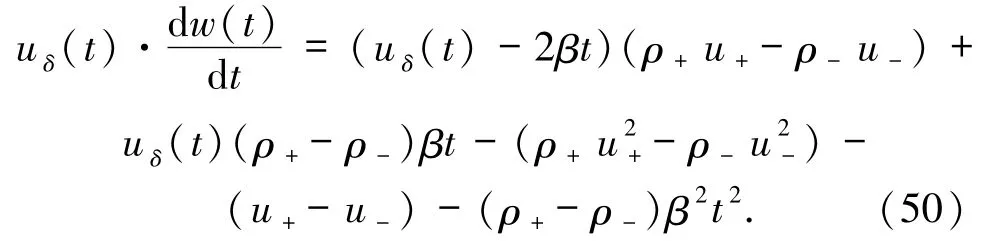
將(48)式代入(49)式得
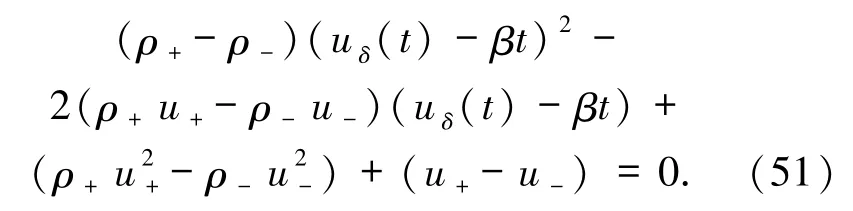
然而,以上得到的δ激波解(46)和(47)在分布意義下需要滿足方程(1),也就是說,需要驗證對于任意檢驗函數(46)和(47)式應該滿足
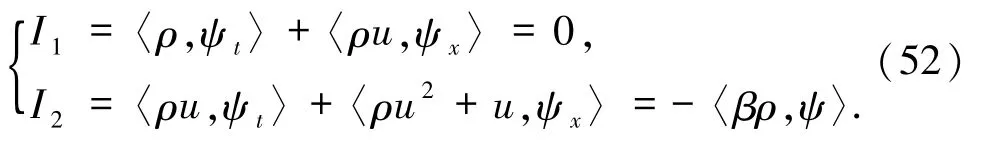
(52)式是方程組(1)的一個弱解.
由(47)式得到δ激波的曲線形式
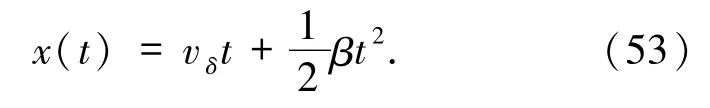
設 vδ>0 且 β >0,對于任意的時間 t,x = x(t)> 0,由(47)式得到
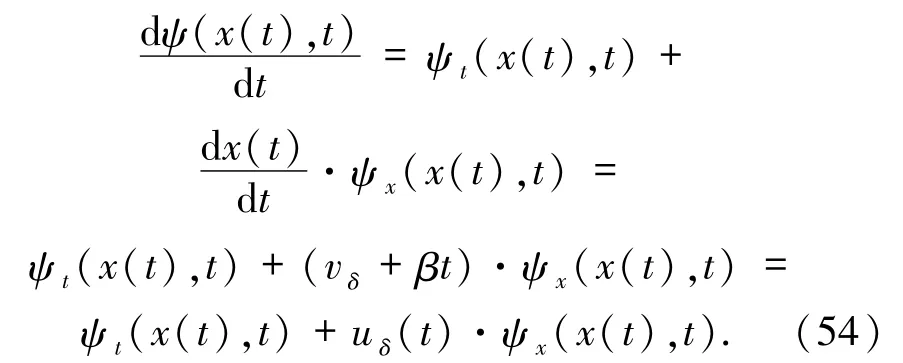
關于(52)式的第1 個方程的證明參見文獻[2].現在,對(52)式的第2 個方程進行分析得到
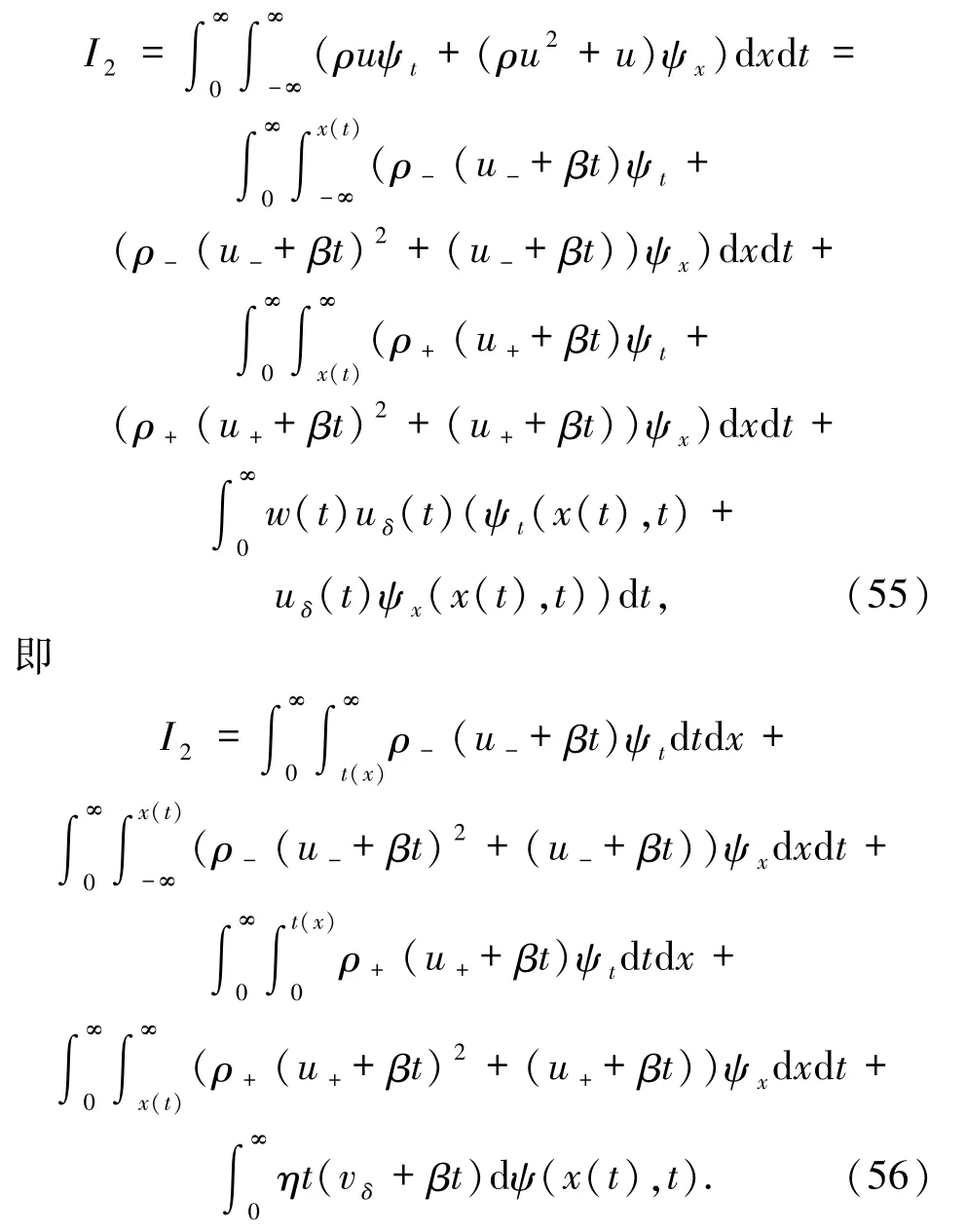
對于上式有
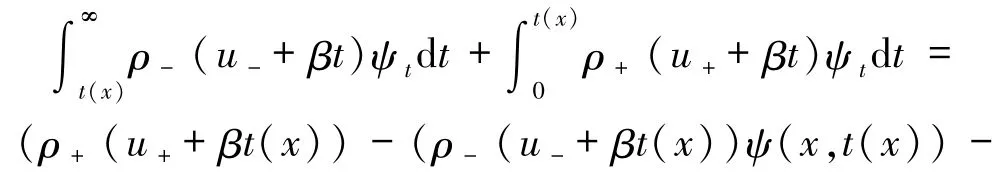
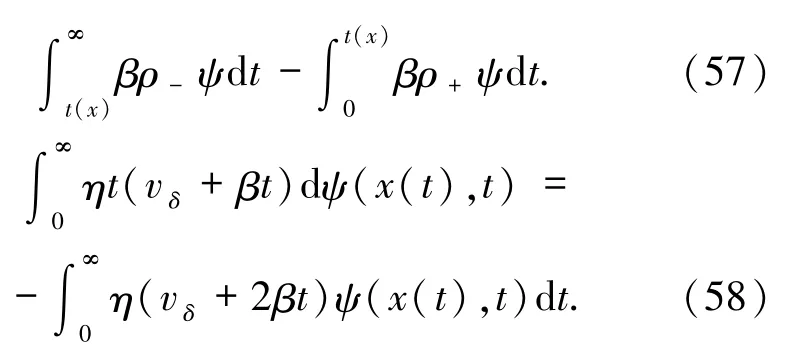
將(57)和(58)式代入 I2得到
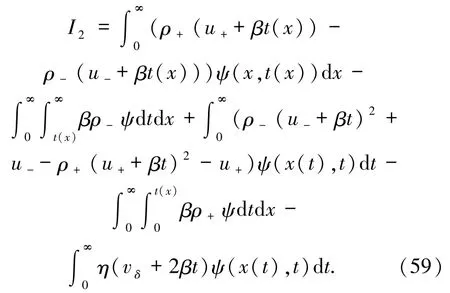
利用變量替換并變換積分順序,I2可以改寫成
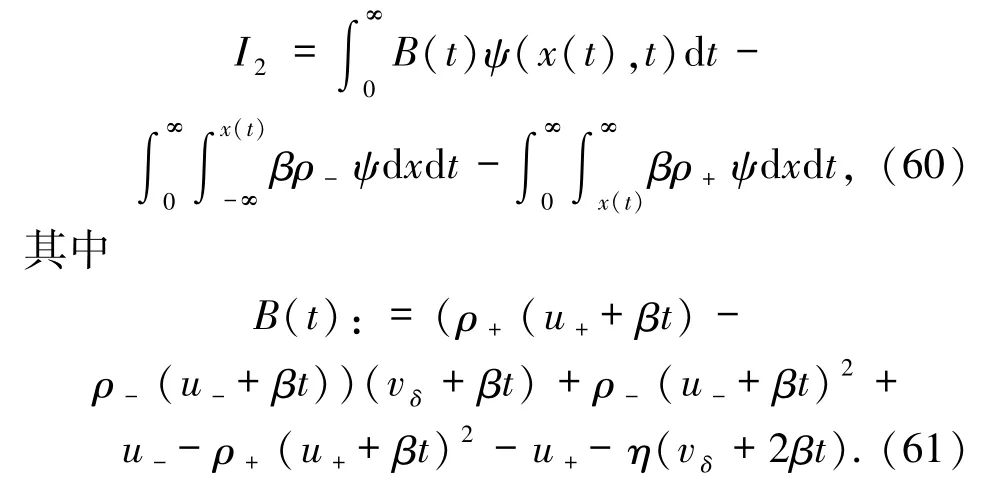
下一步就是計算 B(t),重寫(61)式得到
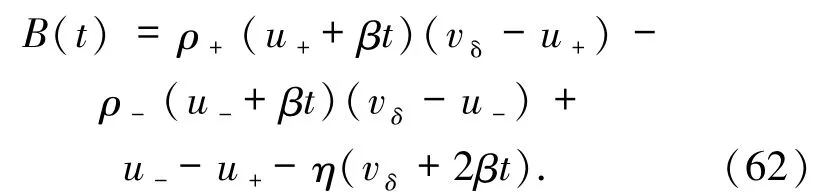
將(32)式代入(62)式得
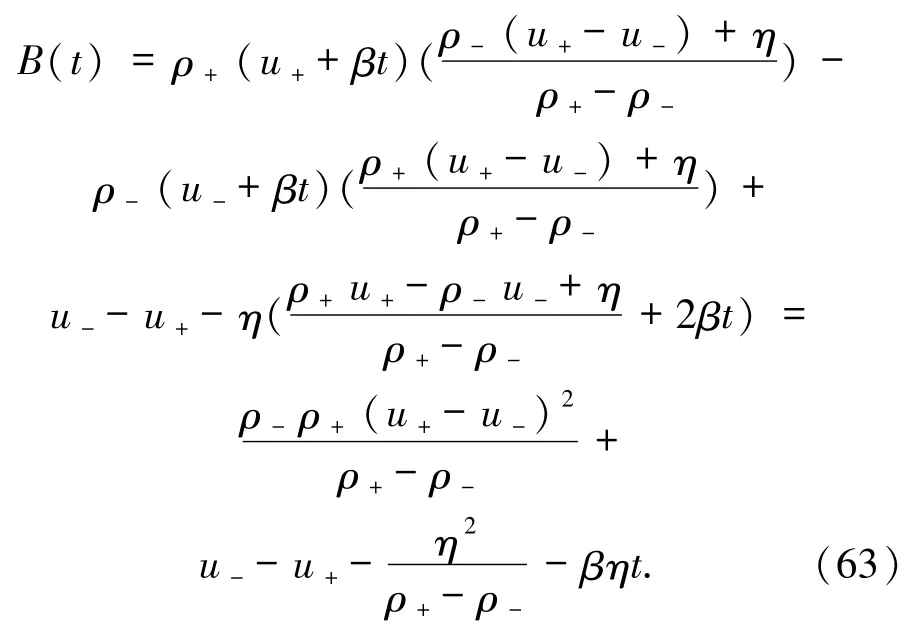
通過將(31)式的 η2代入(63)式得到
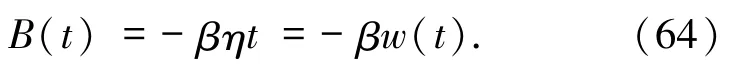
合并(60)和(64)式,可知(52)式的第 2 個方程在分布意義下成立.證明完畢.
注2.1特別的,如果Riemann初值滿足u++且 ρ = ρ ,那么 Riemann 問題(1)和(2)-+的δ激波可以表示成(46)式,并且
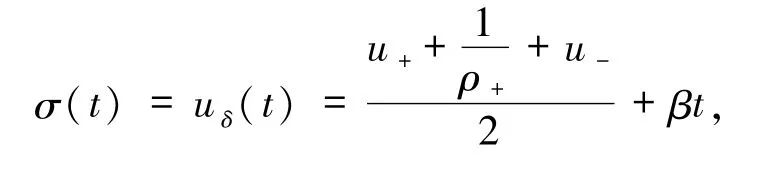
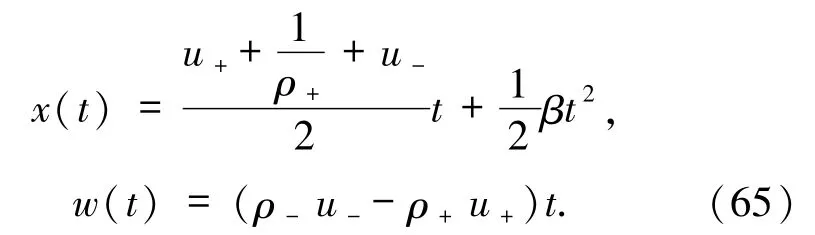
證明過程與前面類似,在這里不再贅述.

