基于Dirichlet 模型的國內COVID-19 疫情數據的Bayesian 估計

楊云源， 楊新平， 張 潔

（1.楚雄師范學院地理科學與旅游管理學院，云南楚雄675000； 2.楚雄師范學院數學與統計學院，云南楚雄675000；3.楚雄醫藥高等專科學校，云南楚雄675000）

截至2020 -04 -10，全國 COVID -19 確診83 369例，海外確診1 537 039 例.疫情在美國、意大利、西班牙、德國等地急劇爆發.通過合理的數學模型，分別計算我國COVID -19 4 個概率指標（治愈概率、重癥概率、病死概率、輕癥概率）和4 個總量指標（累計治愈病例數、現有重癥病例數、累計病死病例數、現有輕癥病例數）的點估計及區間估計分別進行計算，以期為國內和海外COVID -19 疫情監測、指標估計和疫情阻斷提供參考.

與治愈率、重癥率、病死率、輕癥率相關的研究，主要集中在疫情數據描述統計和疫情相關指標預測（估算）上.

1）疫情數據描述統計.如中華預防醫學會COVID-19 防控專家組［1］基于截至 2020 -02 -10 的42 780 例確診病例數據統計，指出COVID -19 病死率為2.38%，合并基礎疾病的老年男性病死率較高.中國疾病預防控制中心COVID -19 應急響應機制流行病學組［2］對截至2020 -02 -11 的72 314例4 類病例的年齡、性別、旅居史等進行回顧性分析，揭示疫情自首次報告病例日后30 d 蔓延至31個省（區/市），粗病死率為2.3%.

2）疫情相關指標預測（估算），主要圍繞再生數、感染規模、倍增時間等估算展開.如Wu 等［3］使用馬爾科夫-蒙特卡洛法（MCMC）估算武漢COVID-19 再生數為2.68，流行倍增時間為6.4 d.陳端兵等［4］使用蒙特卡洛法（MC）依據少量患者的癥狀出現時間對有效再生數進行估計，表明我國在防控措施出臺兩周內，COVID-19 傳播得到了有效遏制.其他方法如：使用 SEIR 或修正 SEIR 模型［5-7］、自回歸移動平均模型（ARIMA）［8］、隨機傳輸模 型［9］、最 大 似 然 法［10］、自 助 抽 樣 法 （Bootstrap）［11］進行 COVID-19 疫情估算.以上文獻中，文獻［1 -2］基于病例數據的統計分析較全面，描述統計結果具有一定的可信度；模型使用中，主要針對再生數、感染規模等進行估算；參數確定直接關乎模型精度，如文獻［5 -6］對相同研究區（湖北省、武漢市）使用相同方法，不同參數得到不同估算結果；文獻［7］的疫情估算使用數據、方法較全面，首次使用了AI技術，預測國內疫情于4 月底結束.對于COVID-19 的治愈率、重癥率、病死率、輕癥率等重要指標，主要通過描述統計來量化，通過模型估計的較少.

Bayesian方法在醫學運用方面，高文龍等［12］、張繼巍等［13］分別簡要介紹了 GeoBugs、OpenBugs在醫學中的應用方法.貝葉斯方法可以量化給定數據條件下的不確定性參數值，借助先驗信息和數據信息可提高數據分布參數的量化精度［14］.如 Yarnell等［15］將貝葉斯分析用于危重病醫學中.Thall［16］將Bayesian方法用于癌癥術后發病率估算與藥物劑量確定.Li等［17］使用Bayesian方法來確定不同非藥物療法對失眠癥的療效和安全性的差異.

對疫情指標采用概率意義下的可信區間估計不僅能得到誤差限而且精度高，有一定的實際意義.本研究根據國家衛建委2020 -01 -20 至03 -28 公報數據，建立 Bayesian 框架下的 Dirichlet 模型，通過MCMC 方法進行求解，得到逐日4 個概率指標（治愈概率、重癥概率、病死概率、輕癥概率）的點估計與區間估計，進一步計算逐日4 個總量指標（累計治愈病例數、現有重癥病例數、累計病死病例數、現有輕癥病例數）的點估計與區間估計，并進行誤差分析，給出了估計誤差限.以期研究方法與結果能為國內和海外COVID -19 疫情監測、指標估計和疫情阻斷提供參考.

1 數據和方法

收集國家衛建委2020 -01 -20 至03 -28 公布的累計確診病例數n、累計治愈病例數c、現有重癥病例數e、累計病死病例數d數據.累計輕癥病例為 m，則

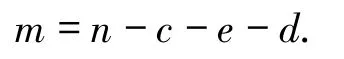
將 n、c、e、d、m 視為總體，第 t天的觀測值分別記nt、ct、et、dt、mt.2020 -01 -20 至 01 -22 共 3 d 公報數據中的e1＝0、d1＝0，并且 3 d 的新增治愈數為0.所以本研究使用的樣本數據為2020 -01 -23 至03 -28 共66 d的日報數據.

COVID-19 確診病例逐日病情診斷、治療康復出院前核算檢測都需要一定的時間，加之前期檢測試劑、醫療資源短缺，上報全國的疫情的各項日報指標值工作量較大.數據的誤差可能是來自隨機因素，也可能是系統誤差，該誤差不能消除，只能設法減小［18］，采用可信區間對COVID -19 疫情指標進行估計就變得更有實際意義.用帶有一定誤差的數據對治愈率、重癥率、病死率、輕癥率等相對指標進行計算，誤差會累積，而Bayesian框架下的Dirichlet分布是解決此類問題的有力的工具.將國家衛健委公布的累記確診病例數視為當日的獨立試驗次數（當日每個確診病例病情變化視為一次實驗過程），結合試驗的結果（日報值），以多項分布為基礎，建立Bayesian框架下的Dirichlet模型，借助數據信息及先驗信息，通過Gibbs抽樣方法得到總體參數的后驗樣本，采用MCMC方法得到治愈概率pt1、重癥概率pt2、病死概率pt3及輕癥概率pt4為參數的Bayesian 估計，進一步計算總量指標（治愈病例數、重癥病例數、病死病例數、輕癥病例數）的Bayesian點估計和區間估計.使用軟件為Eviews、R語言和OpenBUGS.

2 Bayesian框架下的Dirichlet模型的建立

2.1 模型的建立將第t 天累計確診病例數nt視為nt次獨立試驗，當日每個確診病例的病情變化視為一次實驗，每次試驗有4 個互不相容的結果：At1＝“治愈”，At2＝ “重癥”，At3＝ “病死”及At4＝“輕癥”，且只有一種結果發生（無癥狀感染者日報起始于 2020 -04 -01），P（Ati）＝ pti，i ＝ 1，2，3，4.記待估參數為

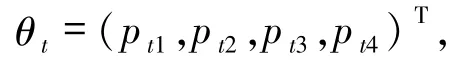
日報數據記為

由多項分布的定義有：

datat～ Multinomial（θt，nt），相應的似然函數為模型（1）

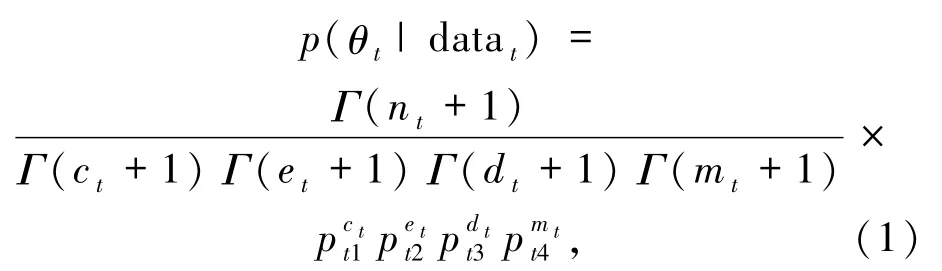
模型（1）中，

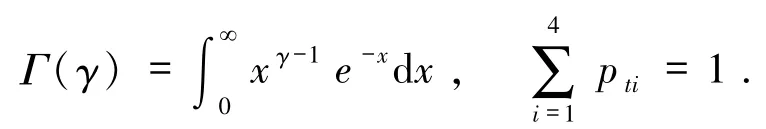
因為參數θt沒有任何先驗信息，按照 Nguyen的理論［19］，選擇 Dirichlet 分布為其先驗分布，第 t天先驗分布模型為模型（2）

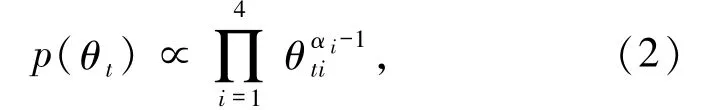
記 α ＝ （α1，α2，α3，α4）T，從而得到θt的后驗精確分布

θt～ Dirichlet（α1+ct，α2+et，α3+dt，α4+mt），

相應的后驗密度函數為模型（3）

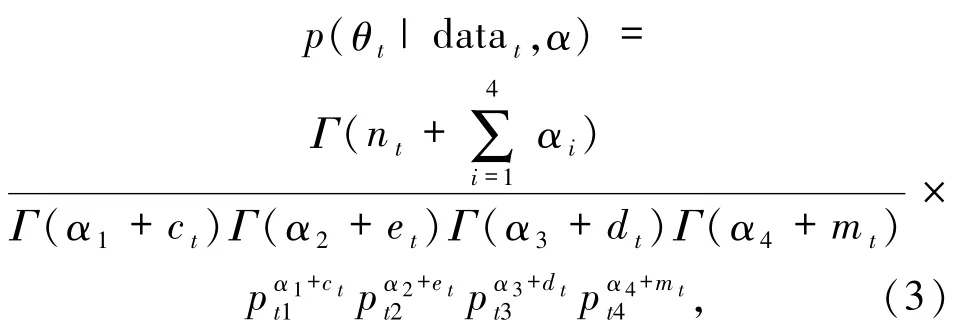
模型（3）中，參數θt沒有任何先驗信息，根據Lunn等的理論［20］，對于先驗分布 p（θt），選擇 α ＝（1，1，1，1）T，該分布等價于四維的均勻分布作為θt先驗分布.分別求出各個參數的滿條件分布p（θti｜θt（-i），datat，α），其中，θt（-i）表示θt中 4 個分量去掉第i個分量后剩下的3 個分量構成的向量.比如

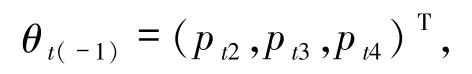
參數θt1相應的滿條件分布為模型（4）

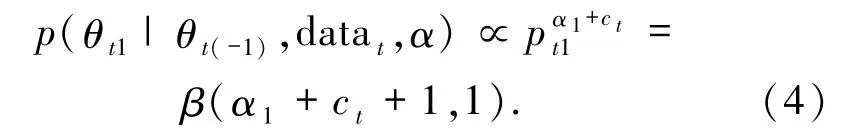
模型（4）是一個標準分布，其他3 個滿條件分布與之類似，可以采用Gibbs 抽樣得到全部參數（計 66 ×4 ＝264 個參數）的后驗樣本，形成 264 條MC鏈，完成Bayesian推斷.

2.2 模型的求解在OpenBUGS 環境下進行模型求解.由于參數個數較多，設定隨機數種子后，由軟件自動生成參數的迭代初始值.為降低后驗樣本間的自相關性、同時又確保馬氏鏈（MC 鏈）收斂，取間隔抽樣步長為100，燃燒期為5 000，進行105次迭代Gibbs抽樣，得到264 個待估參數的后驗樣本（264 條MC鏈）.扔掉燃燒期的前4 999 個樣本后，用剩余的95 001 個樣本通過MC 方法完成對參數θt的Bayesian推斷，相應的參數估計值（表1）包括：均值估計標準差（σ）、MC 誤差（εMC）、中位值估計（Median）及95% CI（可信區間）.同時將逐日 4 個參數（pt1、pt2、pt3及pt4各 66 個 Bayesian 估計）列表顯示，表中“…”表示中間的行省略.

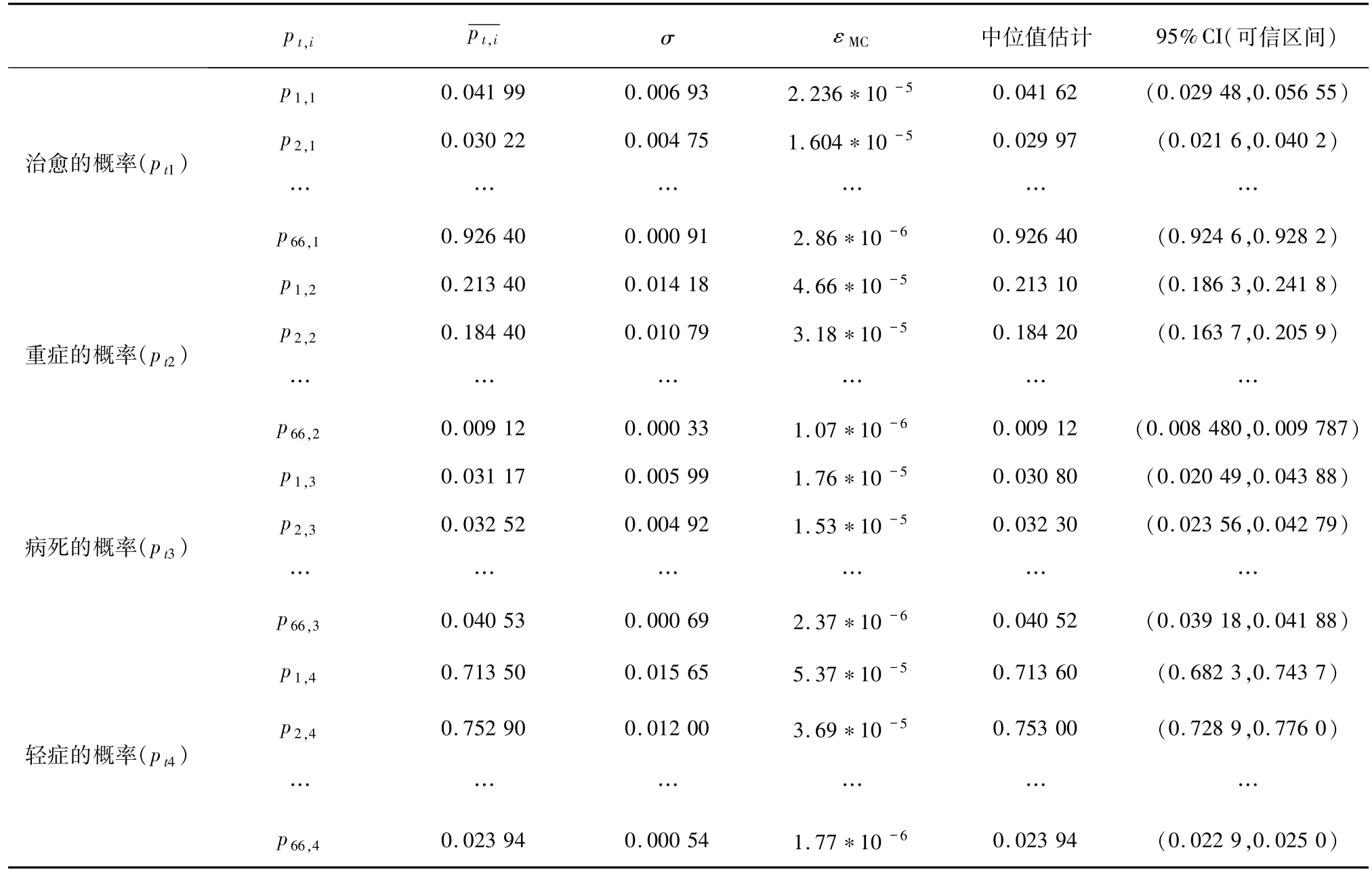
表1 參數θt的Bayesian估計及部分統計量匯總表Tab. 1 Summary of Bayesian estimation and partial statistics of θt

2.3 模型診斷對于模型（3）中的264 個參數，分別繪制History-strace-plot圖、核密度估計曲線圖和 Autocorrelation 圖（以p1，1和p66，4為例，見圖 1，其余的262 個圖略，下同）. 264 個參數的 History -strace-plot 顯示，前4 999 個燃燒值樣本舍棄后，264 條MC鏈均收斂，且極限分布都是各自的后驗分布，適宜用相應的MC 鏈作為后驗樣本進行統計推斷.通過后驗樣本，分別求出參數pt，1至pt，4，t ＝ 1，2，…，66 的后驗核密度估計（圖 1 C -D，以p1，1和p66，4為例），結果顯示參數的分布呈對稱性，以正態分布為近似分布，后驗均值與中位值幾乎相等.每一條 MC 鏈的自相關圖（圖 1 E -F，以p1，1和p66，4為例）顯示，在滯后期≥2 以后，自相關系數接近于0，所以每一條鏈均可視為獨立同分布的MC 鏈，樣本均值成為一致、有效、無偏的估計. 264 個參數的εMC均小于5.37 × 10-5. pt1、pt2、pt3及pt4最大εMC對應的相應數據信息見表 2.表 2 中（max｛εMC｝／σ）×100%最大值僅為0.774 55%，說明模型（3）具有較高的精度［19］.最大的εMC發生的時點均是2020 -01 -23，最大εMC對應4 個概率全部集中在2020 -01 -23；而且在2020-02-13前，樣本計算得到的指標數據波動較大，后期逐漸光滑.說明2020 -02 -13前的日報數據誤差明顯大于后面的日報數據誤差，再次說明區間估計的重要性.由各自的可信區間計算得到pt1、pt2、pt3及pt4點估計的最大誤差限分別是0.013 535、0.027 7、0.011 695 及 0.030 7，預測誤差最大發生的時點也是2020 -01 -23.

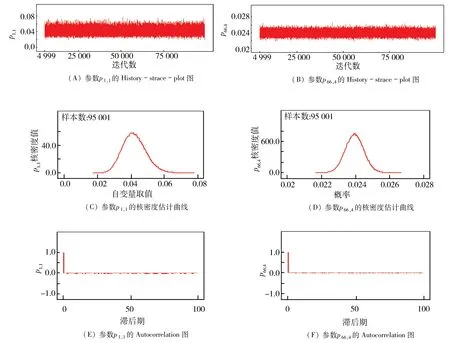
圖 1 參數p1，1和p66，4的 History-strace-plot圖、核密度估計曲線和 Autocorrelation 圖Fig. 1 History-strace-plot，Kernel density estimation curve and Autocorrelation of parameters p1，1 and p66，4

表2 模型（3）的各條MC鏈的最大MC誤差及相應數據信息匯總表Tab. 2 Summary of maximum MC error and corresponding data information of each MC chain of Model（3）

采用概率意義下的可信區間對疫情指標進行估計，精準性更高.它不僅給出每個日報指標的下限，而且給出上限及誤差信息，同時，可信區間能覆蓋指標的直實數據值.為此，利用模型求解過程中得到了264 條MC鏈（每條鏈都收斂于各自的后驗分布），采用MC 方法得到相應參數的估計及統計量.然后提取逐日4 個概率的2.5%的后驗分位數和97.5%的分位數繪制各自95%的可信區間，從而得到逐日4 個概率的95%的可信區間帶.

3 結果與分析

3.1 治愈概率 、重癥概率、病死概率及輕癥概率估計本文2.3 模型診斷結果，充分說明模型（3）對于疫情的相對指標（4 個概率）估計的合理性與精確性，為了進一步將模型（3）的估計結果（概率）和樣本計算的結果（頻率）作對比分析.記fti（i ＝1，2，3，4）分別表示第 t 天樣本計算的治愈頻率、重癥頻率、病死頻率和輕癥頻率.第 t 天相應概率Dirichlet模型（3）計算得到的中位值估計（ptif），數值結果見表 1，分別用qtil和qtiu（i ＝1，2，3，4）分別表示概率ptif的95%的可信區間的下限和上限，并用計算結果繪制相應的頻率，概率曲線及95%可信區間帶（圖2）.

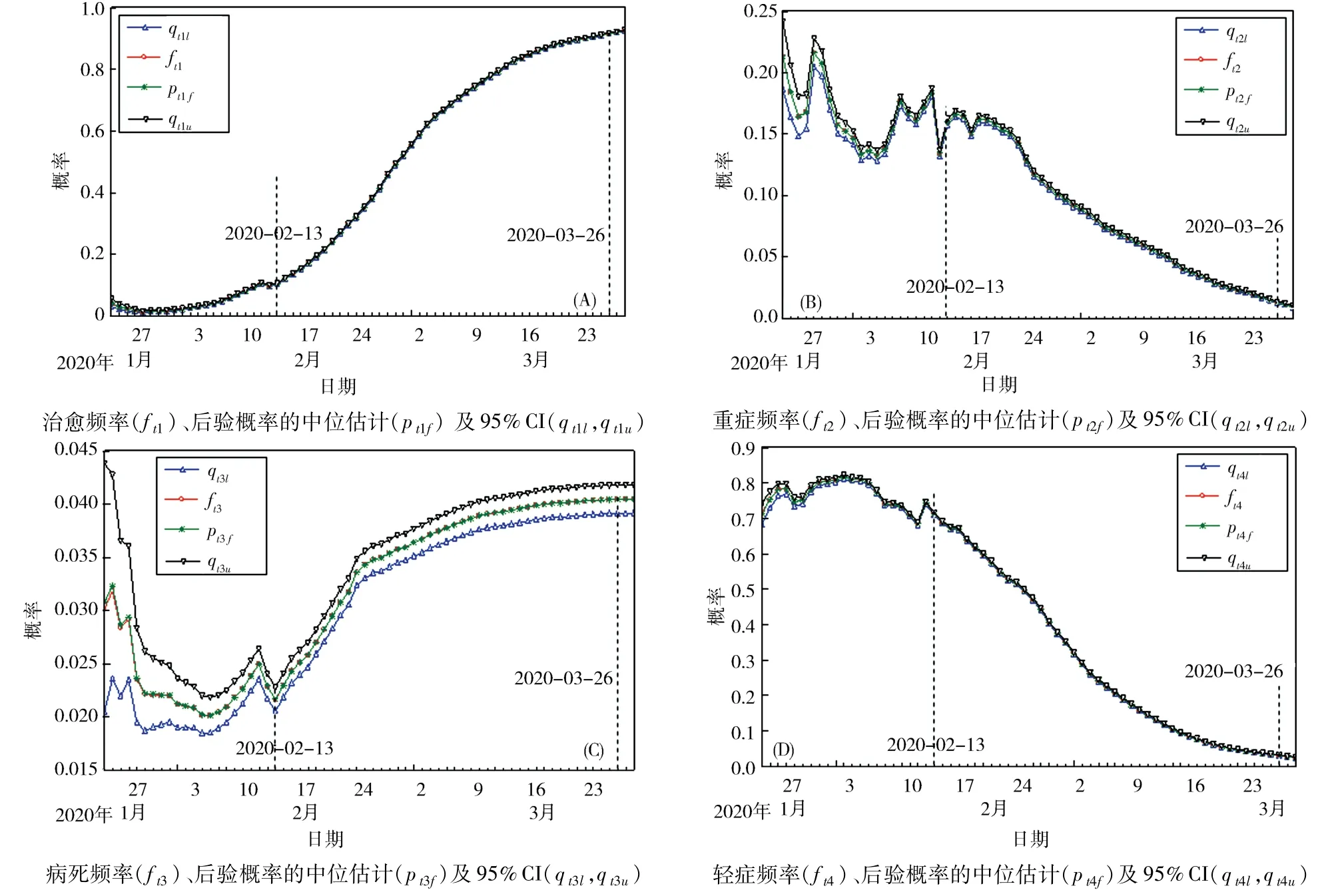
圖2 治愈頻率、重癥頻率、病死頻率、輕癥頻率及對應的后驗概率估計Fig. 2 Cure frequency，severe frequency，fatal frequency，mild frequency and the corresponding posterior probability estimation

結果顯示：1）同一天的4 個概率和為1；2）除病死概率的可信區間帶略寬，預測誤差略大外，其他三者的可信區間帶較窄，幾乎與預測值曲線重疊，精度較高；3）4 個概率曲線在02 -14 后均呈現出光滑變化特性；4）治愈概率、重癥概率、病死概率及輕癥概率基本上呈現3 個階段的變化特征.第一階段（2020 -01 -23 至02 -13）治愈概率經歷短期下降后緩慢上升，在2020 -02 -11 呈現小幅振蕩；重癥概率在幅度為2.8% ～24.2%的范圍內振蕩；病死概率在幅度為1.84% ～4.39%的范圍內劇烈振蕩；輕癥概率在幅度為68% ～82%的范圍內振蕩.第二階段（2020 -02 -14 至03 -26）治愈概率呈S型曲線逐漸上升，重癥概率在2020 -02 -16經過小幅振蕩后逐步下降，前期（02 -14 至02 -21）下降速度慢度，后期（02 -21 以后）下降速度稍快；病死概率前期（02 -14 至02 -23）上升速度比后期（02 - 23 以后）快，變化范圍為 2. 18% ～4.18%，可信帶稍寬；輕癥概率呈反S 型曲線逐漸下降.第三階段（03 -26后），治愈概率上升到92%以上；因為疫情得到控制，大量治愈病人出院，醫院滯留病人快速減少，重癥概率降到1.2%以下，且呈減少趨勢；病死概率穩定在4%左右；輕癥概率下降到3%以下，并趨于穩定.

3.2 累計治愈病例數、現有重癥病例數、累計病死病例數、現有輕癥病例數估計為簡化公式，記

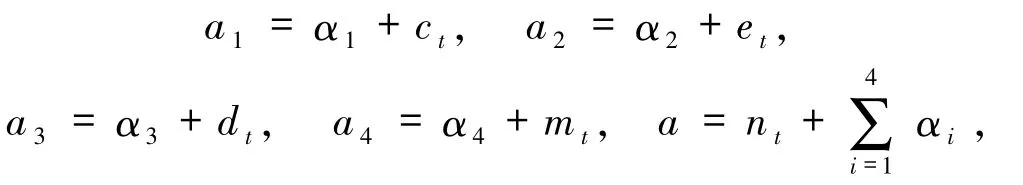
由Dirichlet分布的性質可知

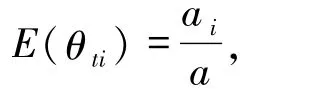
由K-Pearson替換原理，將各自的總體期望用后驗均值估計替代，可得第t 天總體總量指標的Bayesian估計，分別記為累計治愈病例數估計ctf，現有重癥病例數估計etf，累計病死病例數估計dtf，累記輕癥病例數估計（記為mtf）.并借助表1 中概率的可信區間上下限，進一步求各個總體總量指標的95%的可信區間（下限、上限分別在相應符號后加l、u表示.如：累記治愈數95%的可信區間記為95%CI：（ctl，ctu），下同）.將 4 個總量指標點估計及區間估計繪制曲線圖（見圖3）.

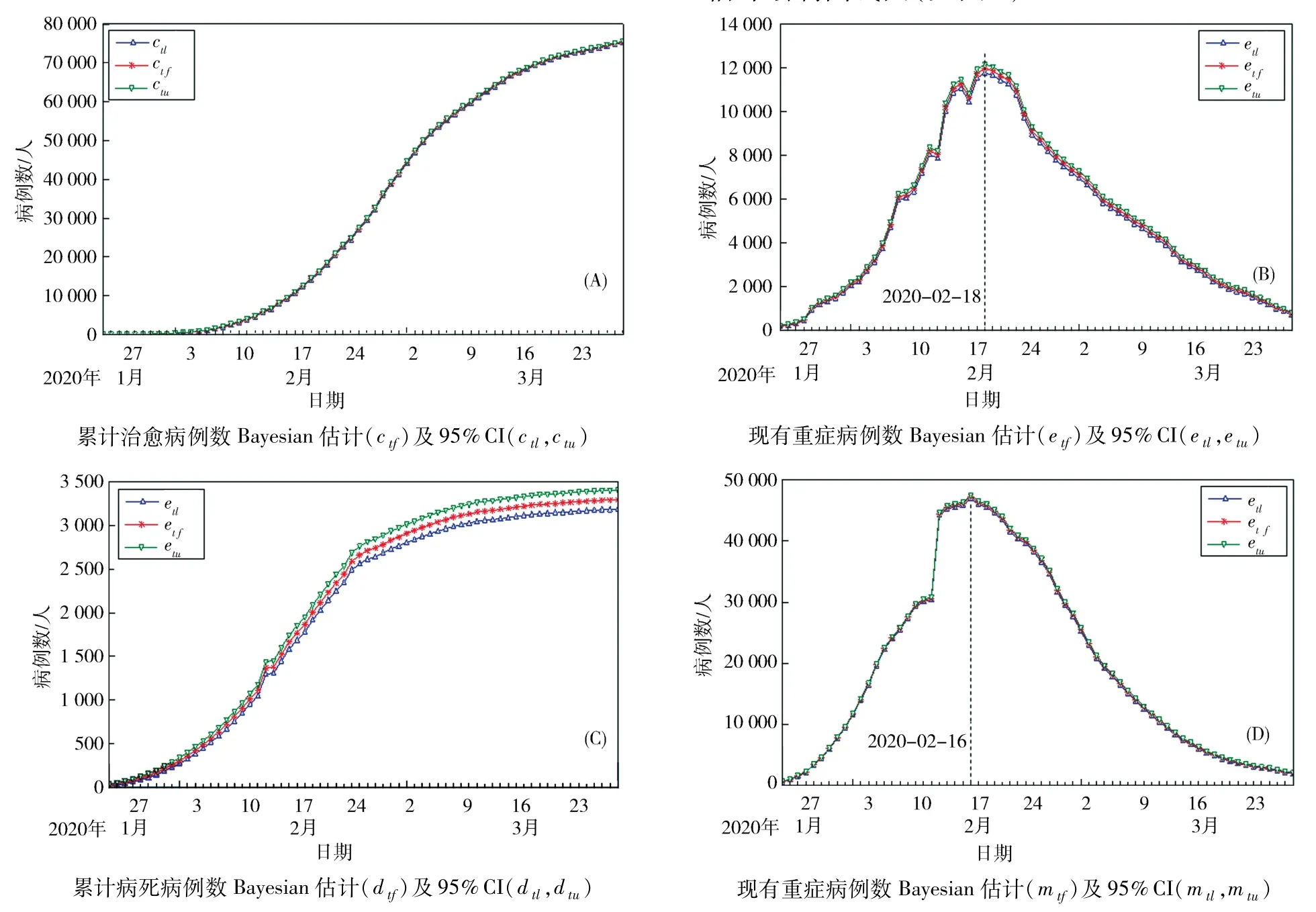
圖3 4 個總量指標估計及對應的95%可信區間Fig. 3 Four total quantity indexes and corresponding 95% confidence interval

結果顯示：

1）除累記病死病例的可信區間帶略寬，預測誤差略大外，其他三者的可信區間帶較窄，幾乎與估計值曲線重疊，精度較高，而且上述四條可信區間帶全部覆蓋了樣本值.

2）累計治愈人數和累計病死人數呈S 型曲線變化.表明醫院治愈病例快速增加，后期進入對重癥集中救治攻堅階段.兩個指標趨于穩定，略呈上升趨勢.重癥病例數以2020 -02 -18 為分界，前期為增長階段，含 3 個振蕩時點（02 -07、02 -12、02 -16），間隔期分別為5 d.后期為下降階段，下降速度慢于前期的增長速度.輕癥病例數以2020 -02 -16 為分界，前期為增長階段，含一個跳躍時點（02 -12）.該值是第四版診療方案向第五版診療方案過渡，臨床病例并入確診病例產生.后期為下降階段，下降速度慢于前期的增長速度.

3）將圖3 中的4 組數據分別提取出來進行對比分析，發現絕大多數時點的Bayesian 點估計和樣本觀測值幾乎一樣，誤差也較小.

為了反映總量指標的預測精度，將累計治愈病例數、現有重癥病例數、累計病死病例數和累記輕癥病例數預測誤差限最大的4 個時點及對應的值提取出來匯總成表（表3），其他時點的預測誤差限均比該時點的誤差限小.

結果顯示：這4 個指標的點估計的最大預測誤差限為277.141 例，相應的指標是2020 -02 -25的輕癥病例數（樣本值36 852例）.

表3 4 個總量指標預測誤差限最大的時點及對應值Tab. 3 Time and corresponding values of the maximum prediction error limit of four total quantity indexes

66 d逐日4 個指標，共計264 個點估計值，528個區間估計值（下限，上限），無法在一個表中呈現.以樣本截止日2020 -03 -28 的計算結果為例（表4）進行說明.結果顯示：點估計和樣本值幾乎相等，95%CI的上下限之差，點估計誤差限都很小，充分說明用可信區間進行疫情的估計更為合理.

表4 2020 -03 -28 的4 個總量指標Bayesian估計及誤差Tab. 4 Bayesian estimation and error of four aggregate indicators on March 2020 -03 -28

4 結論與展望

建立Bayesian框架下的Dirichlet 模型，借助樣本和先驗信息，通過Gibbs 抽樣方法得到總體參數的后驗樣本，采用MCMC方法計算得到264 個模型參數的Bayesian 估計，即逐日4 個概率指標（治愈概率、重癥概率、病死概率及輕癥概率）的點估計及區間估計；使用Dirichlet 分布的性質進一步計算4個總量指標（累計治愈病例數、現有重癥病例數、累計病死死病例數、現有輕癥病例數）的點估計及區間估計.在Dirichlet模型求解過程中，264 個參數對應264 條 MC 鏈均收斂，最大εMC僅為標準差的0.775%，且極限分布都是各自的后驗分布，適宜用相應的MC 鏈作為后驗樣本進行統計推斷.計算了2020 -01 -23 至03 -28 逐日4 個概率（治愈概率、病死概率、重癥概率、輕癥概率）的點估計（共264個值）和95%區間估計（共528 個值）；治愈概率、病死概率總體呈現上升后趨于平穩趨勢，重癥概率、輕癥概率總體呈現逐漸下降趨勢；2020 -03 -26 后4 個概率指標都趨于平穩.計算了2020 -01 -23 至03 -28 逐日4 個總量指標（累計治愈病例數、現有重癥病例數、累計病死病例數、現有輕癥病例數）的點估計與95%區間估計.4 個總量指標點估計的最大預測誤差限為277.141 例，對應的指標是2020 -02 -25 的現有輕癥病例數（樣本值368 52例）.截至2020 -03 -28，累計治愈病例數、現有重癥病例數、累計病死病例數、現有輕癥病例數點估計誤差限分別為 146. 595、53. 100 8、109.948、85.515 例，對應的95%區間估計分別為：（75 301.20，75 594.39）、（689.881 0，796.082 6）、（3 189.937，3 409.833）、（1 864.045，2 035.075）.

用Bayesian框架下的Dirichlet模型計算逐日4個概率（治愈概率、病死概率、重癥概率、輕癥概率）的點估計與區間估計；計算逐日4 個總量指標（累計治愈病例數、現有重癥病例數、累計病死病例數、現有輕癥病例數）的點估計與區間估計，各自的計算精度均很高.Bayesian 方法還可廣泛運用于更廣泛的領域.