油田注水管網布局優化混合整數非線性規劃模型*

張昕 周星遠 張浩然 梁博文 梁永圖

1中國石油大學（北京）城市油氣輸配技術北京重點實驗室

2東京大學

3長江大學石油工程學院

油田注水系統是油田地面工程的重要組成部分[1]。油田注水系統由注水站、配水間、注水井和連接它們的管道構成，是一個復雜且龐大的水力系統。水經泵站加壓后注入注水管網，經由各配水間分配到各注水井，最后經井筒注入地下以實現保持油層壓力，確保油田穩產的目的[2]。整個注水系統的投資費用主要包括基礎建設費用和運行費用，其中基礎建設費用主要包括干、支線管線費用和注水站、配水間、注水井的建設費用。大部分油田已進入高含水開發期，每天的注水量巨大，注水生產投資較高，降低注水能耗具有必要性。現場生產習慣將大部分精力集中在注水管網運行優化方面，對注水管網拓撲布局優化關注較少，管網一旦建成，在短期內將不會有較大改動，因此在建設初期設計出科學合理的布局方案至關重要。注水管網布局設計是保證注水系統高效運行、合理開發油氣資源的關鍵環節[3]。注水管網布局的合理性會直接影響整個系統的投資，同時布局設計結果也會對管網運行情況產生相應影響，因此對注水管網的合理布局不僅可以降低注水系統的投資成本，又可以進一步為降低注水能耗、提高生產效率奠定基礎。

針對注水管網布局優化方法的相關研究，目前最主要的是分級優化法。尉亞民等[4]通過建立井組最優劃分模型、配水間最優布局模型、注水站站址優化模型進行了油田注水管網的布局優化。王美薇[5]將注水管網簡化為點線組合，首先進行注水井的隸屬關系劃分，然后以管線長度最小的原則確定配水間及注水站的位置并確定管網的拓撲結構。分級優化方法較少地考慮上級優化結果對下級優化的影響，因此根據各級優化結果得到的最終解很難保證是全局最優解。此外，也有學者通過建立整個管網的數學模型求解該問題。劉揚等[6]在油氣集輸管網中以管道總長度最小為目標，采用混合遺傳算法求解，類似方法也可應用于注水管網布局優化中。齊晗兵等[7]將注水站、配水間、注水井簡化為平面中的點，建立了樹狀注水管網的布局優化模型，并引入類電磁機制算法進行求解。武曉勇[8]采用改進蟻群算法確定注水井與配水間、配水間與注水站的連接關系。任偉建等[9]以注水管道總長度最小為優化目標，采用改進粒子群優化算法進行求解。以上研究均證實了優化算法求解的便利性及結果的可行性，但大多以管道總長度作為衡量投資的指標，較少考慮管徑對管道建設投資的影響。

本文在基于普遍應用的單干管多井配水工藝[1]的基礎上，首先運用模擬退火遺傳算法劃分注水井區域并確定配水間的最優位置，然后以加權距離最短為目標，運用Dijkstra 算法確定最終的注水管網拓撲結構。

1 油田注水管網

油田注水管網常見的網絡形態主要分為三種：星形管網、樹狀管網和環狀管網[10]，如圖1 所示。在星狀管網中節點與其所管轄的下屬節點間呈星狀連接；環形注水管網即配水間與注水站以及各配水間連接成環形，注水井分別連接到環形管網上[1]；樹狀注水管網即所有注水井與配水間呈星狀連接，各配水間與注水站間以樹枝狀連接，即配水間之間可以相互連接。

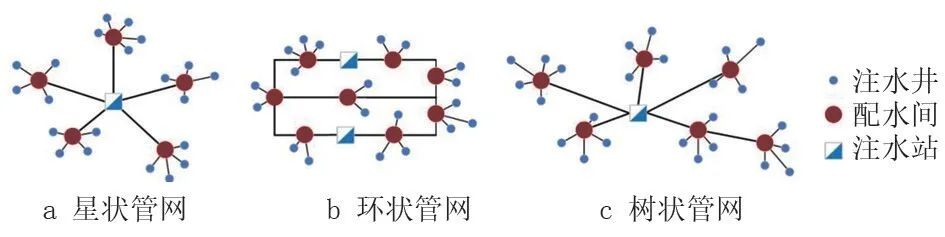
圖1 三種注水管網網絡形態Fig.1 Configuration of three types of water injection pipeline networks

以上三種是油田注水管網的主要形態，對比以上三種管網形態，環狀管網相比其他兩種管網具有造價較高的特點。樹狀管網較星狀管網更為靈活，相比環狀管網具有注水量易于控制等特點[11]。在實際生產中也存在其他形態的管網，可根據實際情況對管網的拓撲結構做出相應調整。

2 注水井組劃分及配水間站址優化

2.1 數學模型

2.1.1 目標函數

先前的研究大多以距離總和最短近似代替管網建造費用最低的目標，較少考慮管徑對于管網造價的影響。因考慮到注水井產量不同會導致上級配水間的處理量以及連接它們之間的管徑不同，注水井的位置不同也會導致配水間的位置以及連接管道的管長發生變化，均會對注水井的分組效果產生影響，本文引入“加權距離”作為目標函數。根據經濟流速法[12]初算管徑，在各支線流速相差不大的情況下管徑D2與流量qh近似成正比關系，又因管道單位長度造價與管徑尺寸呈線性相關，因此可認為管道單位長度造價與成正相關關系[13]。在注水管網初步布局優化中，可將“加權距離”近似作為管網建設投資的衡量指標。結合以上考慮的因素，將流量作為權重建立注水井組劃分與配水間站址優化數學模型［式（1）］，目標函數為各配水間到其所管轄注水井的加權距離之和最小。

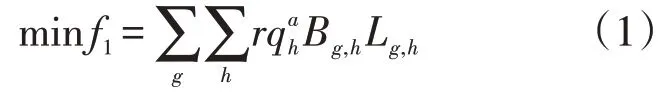
式中：qh為第h個注水井的產量；Lg,h為第g個配水間與第h個注水井之間的距離；Bg,h為判斷第g個配水間與第h個注水井之間連接狀態的二元變量，若第h個注水井屬于第g個配水間，則Bg,h=1，否則Bg,h=0，不計入加權距離計算范圍之內；γ和α分別為加權系數和指數，一般γ=1，α=0.5[13]。

2.1.2 約束條件

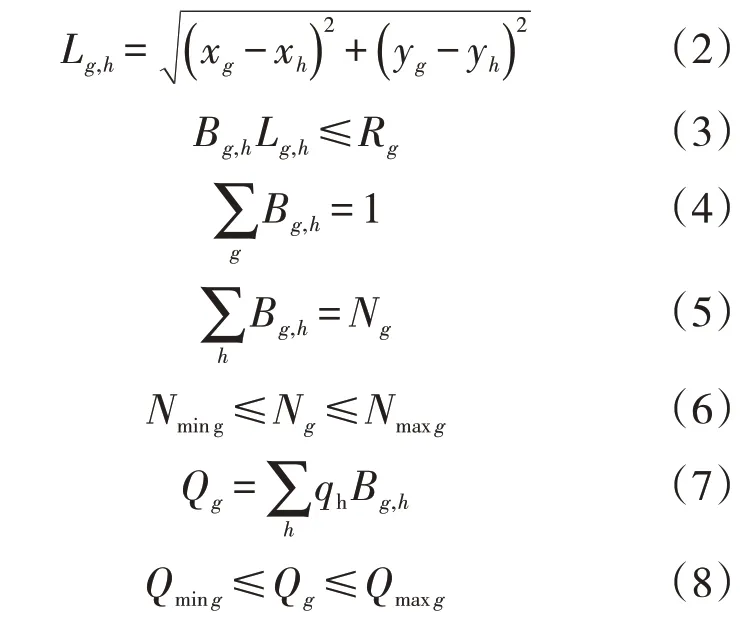
式（2）表示第g個配水間與第h個注水井之間的距離，其中(xh，yh) 為注水井h的坐標，(xg，yg)為配水間g的坐標；式（3）為配水間管轄范圍的約束，其中Rg為配水間配注范圍限制；式（4）為注水井隸屬關系的唯一性約束，即每個注水井只能歸一個配水間管轄；式（5）、（6）表示配水間管轄注水井的數量約束（一般為3～8 口）；式（7）中Qg為第g個配水間配注流量，該式表示配水間流量為其所管轄注水井流量之和；式（8）表示配水間配注流量需滿足一定的范圍需求，其中Qmaxg為配注流量上限，Qming為配注流量下限。

2.2 模型求解

由于本文所建立的注水井組劃分與配水間站址優化模型為混合整數非線性規劃模型（MINLP），采用常規的數學規劃算法難以在常規時間內求得有效解，并且所建立的模型中實際包括兩個子問題，分別為注水井組劃分與配水間站址優化，兩個問題互相耦合，即劃分注水井組需已知配水間位置，而確定配水間最優位置又需已知其所需要管轄的注水井。本文選擇耦合模擬退火算法（Simulated Annealing，SA） 與遺傳算法（Genetic Algorithm，GA）的模擬退火遺傳算法（Simulated Annealing Genetic Algorithm，SAGA）[14]對所建立的模型進行兩階段求解。模擬退火遺傳算法利用遺傳算法較強的全局搜索能力以及模擬退火算法較強的局部搜索能力對模型進行求解[15]。父代完成選擇、交叉、變異等遺傳操作后產生子代，采用模擬退火算法對子代中配水間位置進行局部搜索，產生最終子代后再次按照遺傳算法的流程進入下一代。

第一階段由遺傳算法負責求解注水站與配水間的隸屬關系，因為作為求解離散變量組合優化的經典算法，采用遺傳算法劃分注水井組具有良好的匹配性與適用性；第二階段在配水間與注水井隸屬關系已知的條件下由模擬退火算法負責對配水間位置進行優化，因模擬退火算法具有良好的局部搜索能力，在初始較優解（所管轄注水井的加權中心位置）已知的情況下能較快收斂得到最優解。同時第二階段的配水間位置優化又能對前一階段的注水井組劃分進行反饋，即若該注水井組劃分方案下，所求得配水間最優位置遠不能滿足相關約束或者目標函數，則證明該注水井組劃分方案較差。

2.2.1 方程確定

（1）適應度函數的確定。采用適應度函數作為衡量種群中個體優劣的唯一標準，適應度函數的選擇會直接影響算法的收斂速度和最終的求解結果。在遺傳算法中適應度函數要求為單值、連續、非負、最大化函數[16]。因配水間站址優化中目標函數為加權距離最小，因此需要對目標函數進行一定的轉化以滿足遺傳算法對適應度函數的要求。若某種配水間站址方案不滿足模型的某個約束條件時，需加入懲罰因子使該方案的適應度變低[17]，從而使得產生子代的概率減小，最終被淘汰，適應度函數的具體表達式如下：

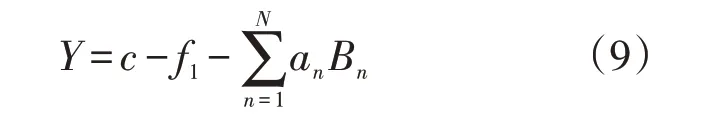
式中：an為不滿足第n個約束條件的懲罰因子；Bn為判斷某個解是否滿足第n個約束條件的二元變量，若不滿足則Bn=1，反之Bn=0 ；c為常數，通過設置合適的c值以保證適應度函數為正值。

（2）編碼方式的確定。遺傳算法的編碼方式有二進制編碼、浮點數編碼、實數編碼等形式，二進制編碼較為常用，且對于注水井組的劃分問題來說，二進制編碼匹配性較好。該步驟需要根據配水間管轄注水井的數量要求確定大致的配水間數量。注水井與配水間隸屬關系與算法編碼對應關系如下：若某注水井屬于某配水間，則對應編碼為“1”，若不歸該配水間管轄，則在對應位置的編碼為“0”，之后將各注水井相對于各配水間的對應編碼進行順序排列；若注水井數量為n，配水間數量為m，則生成長度為n×m的二進制編碼，一串二進制編碼即為算法中的一個個體，代表一種注水井組的劃分方案，如圖2 所示。該編碼方式較為直觀，也便于后續的優化求解。具體求解過程中，注水井組劃分方案即遺傳算法優化中需要判別的約束有注水井隸屬關系的唯一性約束［式（4）］、配水間管轄注水井的數量約束［式（5）、（6）］以及配水間管轄注水井的流量約束［式（7）、（8）］。若所確定的二進制編碼，即GA中的一個個體不滿足以上約束，則需在該個體的適應度方程中加入懲罰函數。

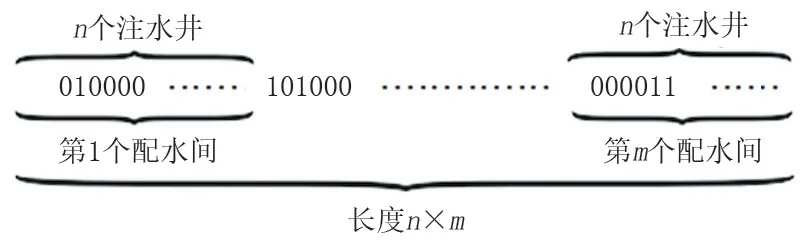
圖2 注水井組劃分方案編碼Fig.2 Coding of water injection well group division

（3）選擇算子。主要有適應度比例法、隨機遍歷抽樣法和局部選擇法。這里采用普遍使用的適應度比例法，是指按一定比例優選出適應度較高的即加權距離最小的注水井組劃分及配水間站址優選方案，保證求解結果的經濟性。

（4）交叉算子。隨機將二進制編碼中幾個位于同一位置的編碼進行交換，這里采用單點交叉方式，在編碼串中設定一個交叉點進行交叉操作，兩種注水井組劃分方案以交叉點為界限，將前或后的部分編碼串進行交換，以產生新的注水井組劃分方案。

（5）變異算子。變異算子即父代方案里的某些基因按照一定概率變成對應的等位基因從而產生不同的子代。這里采用均勻變異的方式，即注水井組劃分方案二進制編碼串的每位基因都有一定的概率執行變異操作。

（6）最優保存策略。每代種群中按照一定比例選擇適應度較高的個體作為父代（即經濟性較高的注水井組劃分及配水間站址優化設計方案），不需要進行交叉變異與模擬退火操作，直接進入下一代種群作為子代，以此提高模型的收斂速度。

2.2.2 求解步驟

采用SAGA求解注水管網布局優化中注水井組劃分以及配水間站址優化方案的計算流程如下：

（1）首先確定初始參數，包括遺傳算法[18]的種群大小、終止進化代數、交叉概率、變異概率；模擬退火算法的初始溫度、終止溫度、每個溫度下的最大迭代次數。

（2）對于隨機產生的注水井組劃分方案進行二進制編碼，產生遺傳算法中的初始種群。

（3）將第k-1 代種群中的每種劃分情況代入適應性函數進行評價。檢查生成的編碼是否滿足管轄范圍以及配水流量的限制，滿足則保留，不滿足則加入懲罰函數，加入懲罰因子使該方案的適應度降低，從而逐漸被淘汰。

（4）進行交叉變異操作，產生第k代種群。

（5）對于第k代種群采用模擬退火算法求解每種注水井組劃分方案（每組二進制編碼）中的配水間最優位置。具體流程如下：在某溫度Tk下設定初始位置，將某一注水井組劃分方案中各注水井的加權中心位置定為配水間的初始位置[9]，按照鄰域函數在該位置附近產生新的位置，并分別計算初始位置與新位置的適應度，若新方案較優，則接受此方案；否則在0-1之間隨機生成一個值，若此值小于，則接受此方案，否則保留原方案，當達到同一溫度下的最大迭代次數后以一定的速度降低溫度。當滿足終止條件時，將最優解輸出，計算結束。采用模擬退火算法求解配水間的最優位置過程中需要判別的約束主要有配水間管轄范圍的約束［式（2）、（3）］。若所確定的配水間位置不滿足配水間管轄范圍的約束，則需要在目標函數中加入懲罰函數。每個注水井組劃分方案下的最優配水間位置所確定的目標函數f1即為該個體的適應度值。

（6）重復步驟（3）～（5）直至達到終止進化代數或得到最優的注水井組劃分及配水間站址優選方案。求解程序框圖如圖3所示。

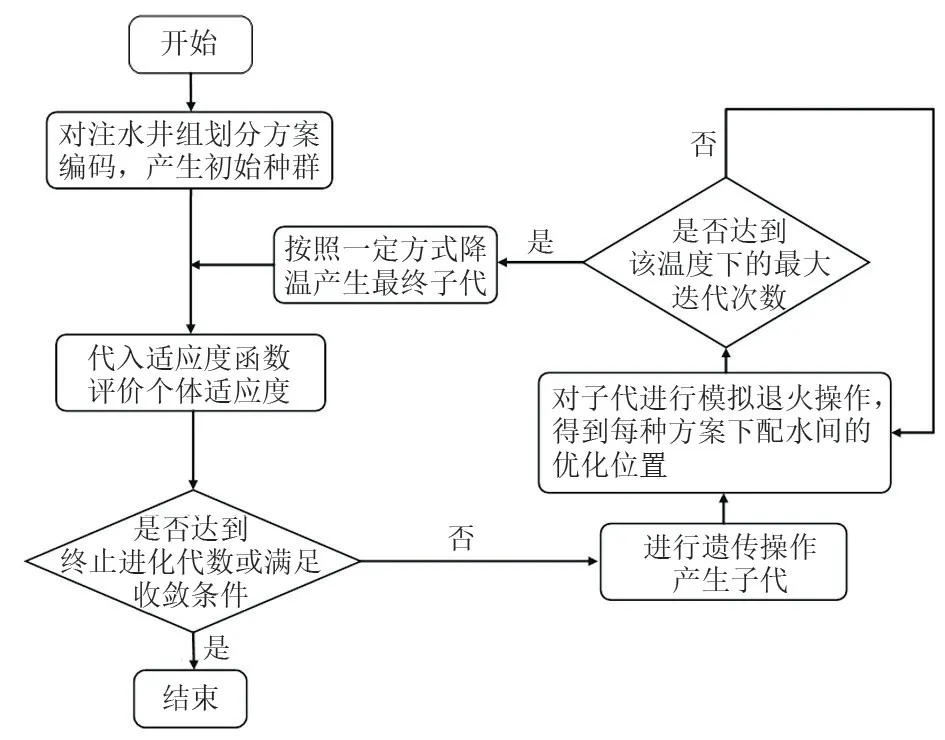
圖3 注水井組劃分與配水間位置優化算法流程Fig.3 Algorithm flow for division of water injection well groups and position optimization of water distribution stations

3 注水管網拓撲結構優化

本文采用Dijkstra 算法確定串接型枝狀管網的拓撲結構[19-20]。

Dijkstra 算法是典型的求解最短路徑的算法，較適用于油田注水管網拓撲結構優化[21]。采用該方法可以求得串接型枝狀管網連接形式下注水站與各配水間相連管段加權距離最小的拓撲結構。

應用Dijkstra 算法[22]確定管網拓撲結構的具體求解步驟如下：

（1）指定計算的起點s，另外引進兩個集合S和U。在計算初始狀態時，注水管網的注水站及各配水間位置已經確定，將注水站位置作為拓撲結構的起點s并放入初始節點集合S中。依次計算s點與其他節點（各配水間）之間的管線建設費用，優選出加權距離最小的形式，將該形式納入到注水管網的拓撲結構中，并將該配水間的位置頂點k 加入S集合中，同時從U集合中移除該頂點。

（2）以納入S 集合中的新的節點作為起始點，選擇出加權距離最小的連接形式納入管網的拓撲結構中，更新S集合與U集合中的點。

（3）重復步驟（1）～（2），直到節點集合S將所有的配水間節點包含在內，形成最終的注水管網拓撲結構。

在采用Dijkstra 算法進行油田注水管網拓撲結構布局中，以“加權距離”作為管網建設投資的衡量指標，最終以此為基礎確定了注水管網的連接形式以及優化得到的拓撲結構。

4 計算實例

整理大慶油田某區塊注水井相關資料，得到注水井位置分布圖，如圖4所示；注水井注入流量信息，如表1所示。根據區塊內所轄注水井數量，每口注水井所需注入流量以及注水站供水能力范圍，將注水站數量定為1座，位置取所有注水井位置坐標的加權中心。采用以上提出的方法進行注水管網的布局優化設計。

在配水間位置優化中，算法基本參數配置如下：種群大小400，終止進化代數500，交叉概率0.85，變異概率0.005，精英個體保留比例10%，初始溫度1 000，終止溫度1，最大迭代次數100。采用MATLAB軟件編程對模型進行求解。根據優化模型計算配水間最優位置，如圖5所示。

圖4 注水井位置及編號Fig.4 Water injection wells'locations and numbers

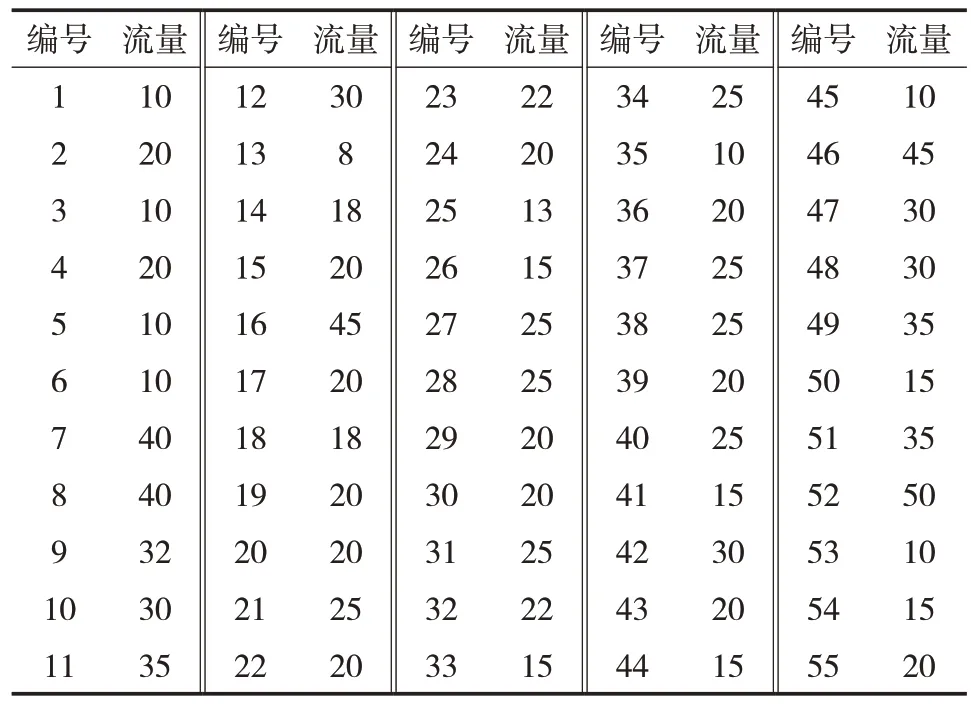
表1 各注水井注入流量Tab.1 Flow rate of each water injection wellm3/d

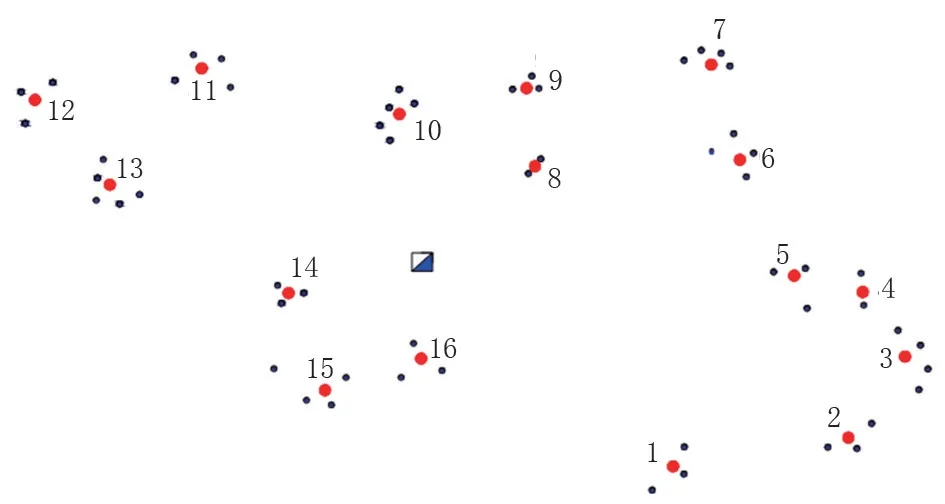
圖5 配水間位置優化結果Fig.5 position optimization resurts of water distribution stations

在管網拓撲結構優化中，將流量以權重形式考慮在內，以管網內管道連接總長的加權距離之和w最小為目標函數，采用Dijkstra 算法得到注水站與各配水間連接管段加權距離最小的管網拓撲結構方案。w的具體表達式如下

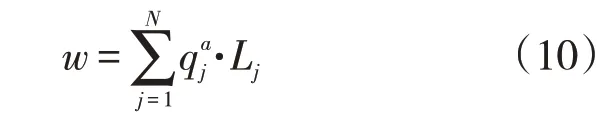
現場管網布局圖如圖6a 所示，經計算其w值為1 423.5m2.5/s0.5。采用Dijkstra 算法計算最終結果如圖6c 所示，目標函數w值為1 269.4m2.5/s0.5，節約管網投資約10.8%。為了便于比較，另采用一般分級優化法進行計算，即首先采用加權中心法進行注水井組的最優劃分及配水間最優位置的確定，其次以w值為目標函數確定樹枝狀注水管網的拓撲結構，最終得到的樹狀管網如圖6b 所示，其目標函數w值為1 335.5m2.5/s0.5，相比原布局方案節約投資約6.2%，可知采用本文提出的方法較其他方法更易得到最優解，本文將注水井組的劃分與確定配水間站址的耦合關系考慮在內，采用模擬退火遺傳算法進行整體優化從而得到配水間的最優位置；其他分級優化方法分步確定注水井組劃分方案與配水間的位置，最終計算結果受初始方案的影響較大，一般無法得到全局最優解。在該算例中，采用本文提出的方法可得到注水管網布局優化設計的經濟方案，具有一定可行性。

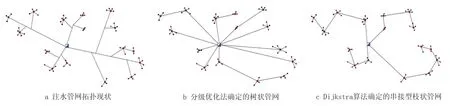
圖6 注水管網拓撲結構對比Fig.6 Comparison of water injection network topologies

5 結論

本文在布局優化設計中，首先針對注水井區域劃分及配水間的站址優化問題建立了混合整數非線性規劃模型，配水間最優位置的確定受注水井組劃分方案的影響，克服了一般分級優化方法較難得到全局最優解的弱點，采用模擬退火遺傳算法進行分階段求解，從而可確定配水間的最優位置；其次采用Dijkstra 算法，以注水站與各配水間加權距離最小為原則確定注水管網的拓撲結構，與現場及一般分級優化方法求解方案進行比較，本文提出的方法節省了注水系統投資，完成了科學、合理且經濟的注水管網布局優化方案。在模型設計過程中將各節點間距離簡化為兩點間的直線距離，尚未將油田實際環境如地形地貌、障礙物等因素考慮在內，這將成為進一步的研究方向。