中低速磁浮道岔車岔耦合振動分析

（西南交通大學 機械工程學院，成都 610031）

0 引言

磁浮列車具有速度快，無噪音，環保等優點，是21世紀理想的超級快車，世界各國都十分重視發展磁浮列車。目前，國內外學者對道岔進行了一系列研究。靖仕元[1]通過對長沙磁浮工程道岔梁安裝阻尼器進行試驗，測量了阻尼器對磁浮道岔減振情況。龔樸[2]對五轉向架磁浮車輛的結構及行駛過彎進行了分析，得到了中低速磁浮車輛運行需求。陳越龍[3]將可靠性技術應用于磁浮道岔中。Jong-Boo Han[4]進行了車輛在磁浮道岔上懸浮穩定性研究。以上論文主要研究了磁浮列車及道岔的設計，實驗中的表現，可靠性的研究，而很少對磁浮道岔進行耦合振動分析。磁浮道岔是磁浮列車行駛過程中的薄弱環節，道岔梁的主要材料是Q235，因為這種鋼結構沒有阻尼，在軌道不平順及磁浮列車的懸浮電磁鐵及空氣彈簧的振動影響下，車輛-道岔容易發生耦合振動，造成打軌或更嚴重事故。因此對磁浮道岔進行耦合振動分析具有重要意義。

磁浮道岔的穩定性對磁浮車輛行駛過程中的人員安全至關重要，道岔的剛度和強度必須滿足要求，道岔自身的結構特性也應能承受車輛行駛引起的振動變形。本文以某26.5m中低速磁浮道岔為研究對象，分析道岔的振動情況。

磁浮道岔結構部分主要由主動梁、第一從動梁、第二從動梁、固定端垛梁、活動端垛梁、梁間豎向支承滑動裝置等部分組成[5,6]，如圖1所示。

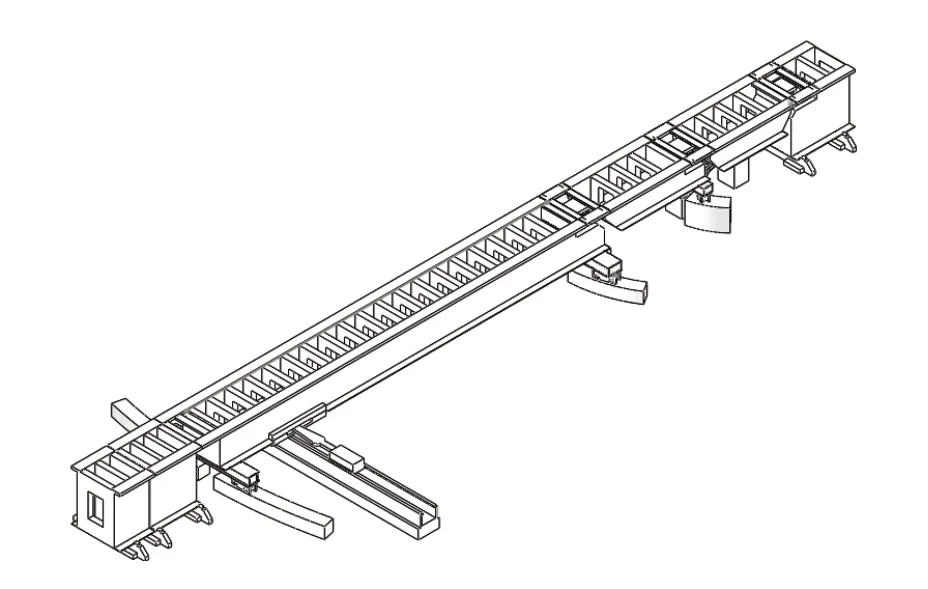
圖1 磁浮道岔的結構模型

1 磁浮道岔縱向等效剛度分析

道岔梁由三段梁和三個連接板構成。磁浮列車在磁浮道岔上行駛時，依次經過連接板三，第二從動梁，連接板二，第一從動梁，連接板一，主動梁。

磁浮列車在磁浮道岔上行駛時，懸浮架上的懸浮電磁鐵對道岔梁產生均勻壓力。磁浮列車行駛至每節道岔梁邊界附近時，由于其下有支座支撐，道岔梁變形較小；當磁浮列車行駛至道岔梁正中時離支座最遠，所以此時其豎向變形最大。設道岔梁豎直方向上的變形與列車過岔行駛距離的函數關系為x（l）。

因為磁浮列車行駛時，道岔梁的載荷是變化的，為了得到磁浮道岔縱向等效剛度，將整個道岔梁分為6節，并分別對每節梁上選取30個等距的應變測量點。然后使用有限元軟件ANSYS對磁浮道岔進行靜力學仿真計算，計算后分別記錄每節上所有測量點應變x的數值，為分段擬合做準備。

對于第一節道岔梁，因為不知道x1（l）的具體形式，而知道一些節點l1，l2，…，l30處對應的函數值x1（l1），x1（l2），…，x1（l30），進而知道了x1（l）對應曲線的大致趨勢[7]。假設函數系所產生的空間中的函數曲線較適合未知函數x1（l），現要從Φ 中找到一個最適合x1（l）的函數即在最小二乘曲線擬合中的度量指標——向量的2范數達到最小[7]，即求解

因為當階數n過大時，會產生振蕩現象影響精度，階數過小會導致擬合曲線與原曲線誤差偏大，所以選擇4階多項式擬合。

因為道岔梁在豎直方向上的變形為x（l），列車重量P=320000N，則由P=kx得到剛度與列車過岔行駛距離的函數關系為k（l），即為等效剛度。中低速磁浮道岔等效剛度k（l）圖像如圖2所示。

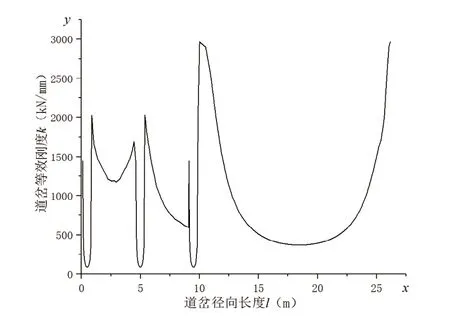
圖2 磁浮道岔等效剛度曲線

2 車岔無阻尼振動特性

2.1 周期性軌道不平順激勵

軌道不平順是指軌道的幾何形狀、尺寸和空間位置相對其正常狀態的偏差，常見軌道不平順的波長范圍為0.01～120m[8,9]。考慮到梁的收縮和蠕變以及溫差引起的上（下）拱，可以認為其不平順近似于正弦曲線，即：

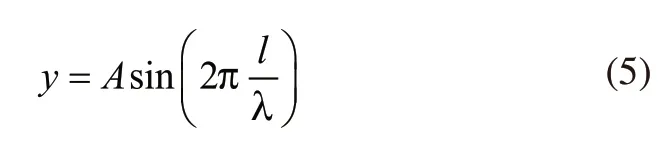
式中，A為不平順幅值；

λ為不平順波長；

L為從初始點到計算點的距離；

Y為不平順高度。

磁浮列車系統對軌道功能區提出了嚴格的制造精度要求，對3個功能面制造安裝精度要求基本上都在1mm以下，故正弦不平順幅值可取為1mm，按列車勻速行駛時進行分析，則從初始點到計算點的距離l可表示為磁浮列車行駛速度v和行駛時間t的乘積。

假定磁浮列車軌道之間的距離恒定，則不平順高度y對時間t求二階導得到磁浮列車在垂向的加速a（t），再乘上磁浮列車自身總質量m=32000kg，即得到列車施加到軌道上的力f關于時間t的函數：

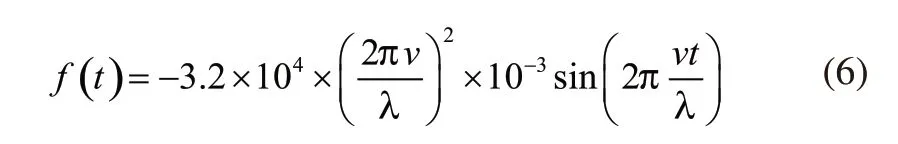
本文取軌道不平順波長λ=3m，將模擬的不同速度v代入式(6)即可得到f（t）表達式。

2.2 無阻尼道岔梁車岔耦合振動分析

因為道岔梁是鋼結構，則道岔梁在振動過程中沒有阻尼作用，磁浮道岔耦合振動的動力學方程如式(7)所示：

式中x為道岔梁應變。

為了簡化計算，采用時域分析。由于中低速磁浮列車通過道岔的運營時速不高于80km/h[10]，則在仿真中取列車運行速度為80km/h，60km/h，40km/h，由l=vt可得f（t）隨磁浮列車行駛距離l的函數表達式f（l）。然后使用MATLAB進行無阻尼磁浮道岔耦合振動仿真分析，其動力學分析原理圖如圖3所示。

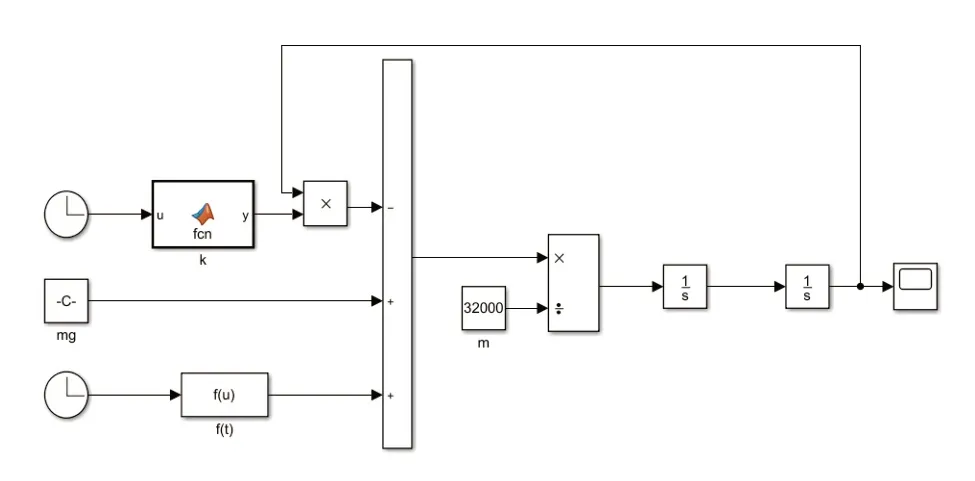
圖3 列車過岔時無阻尼道岔梁振動分析原理圖

動力學分析后得到在磁浮列車以速度為80km/h，60km/h，40km/h通過中低速磁浮道岔時，道岔梁最大應變隨時間變化的函數圖像，如圖4所示。

圖4 列車過岔時無阻尼道岔梁應變曲線

圖4為無阻尼時，道岔梁最大應變的變化曲線，其中曲線1、2、3分別為磁浮列車速度為80km/h，60km/h，40km/h時的道岔梁最大應變曲線。

在磁浮道岔的耦合振動分析過程中，當列車的位置隨時間改變時，道岔梁上各點的垂向位移也在隨時間變化。由列車過岔時無阻尼道岔梁應變圖可以看出振動的曲線由多種振動疊加而成，包括軌道不平順激勵的振動，道岔梁不同位置時的剛度不同而造成道岔梁的反力變化而引起的振動及振動的疊加。在通過26.5m道岔過程中，列車以80km/h，60km/h，40km/h速度通過道岔時道岔梁的最大應變分別為1.91mm，1.59mm，1.23mm。由此可知在磁浮列車通過道岔時速度越快，道岔梁的最大應變越大。因為一般情況下列車過岔的速度不超過80km/h[10]，則道岔梁的最大應變不超過1.91mm，相對于磁浮道岔整體尺寸而言較小，小于危險值，但道岔的變形將影響懸浮電磁鐵的控制系統，從而增大車體的振動，影響車體平穩性，因此減少道岔振動必不可少。

3 有阻尼車岔耦合系統動力學分析

因為道岔梁是沒有阻尼的鋼結構彈性體，則振動容易發生累積。為了減少振動，采用對道岔梁并聯阻尼器的辦法減少磁浮道岔的振動[11]。

粘性阻尼力Fd與振體速度大小相同方向相反，大小為。其中c為粘阻系數，它取決于物體的形狀、尺寸和潤滑等物理性質。磁浮道岔耦合振動的動力學方程如式(8)所示。

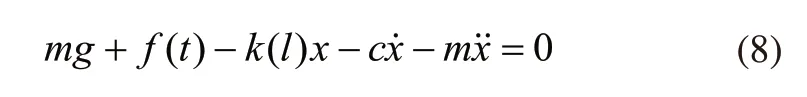
然后對磁浮道岔梁并聯阻尼器進行分析，選擇比較合適的粘阻系數c。然后采用時域分析，使用MATLAB進行磁浮道岔耦合振動仿真分析，其動力學分析原理圖如圖5所示。

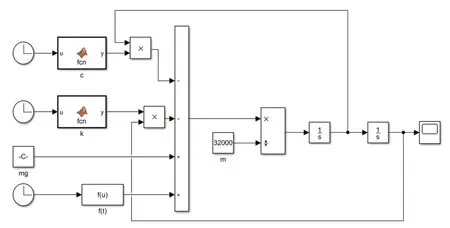
圖5 列車過岔時有阻尼道岔梁振動分析原理圖

動力學分析后得到中低速磁浮道岔在并聯阻尼后，當磁浮列車通過道岔時，道岔梁最大應變隨時間變化的函數圖像，如圖6所示。

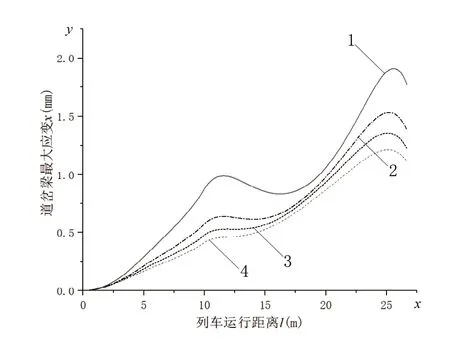
圖6 列車過岔時有阻尼道岔梁應變曲線

圖6為并聯阻尼器后磁浮列車以速度80km/h通過道岔時，道岔梁最大應變的變化曲線。其中曲線1、2、3、4分別表示并聯阻尼的粘阻系數分別為c=0N.s/m、c=1×105N.s/m、c=2×105N.s/m、c=3×105N.s/m時的道岔梁最大應變曲線。

在磁浮道岔的耦合振動分析過程中，當列車的位置隨時間改變時，道岔梁上各點的垂向位移也在隨時間變化。由列車過岔時道岔梁應變圖可以看出振動的曲線由多種振動疊加而成，包括軌道不平順激勵的振動，道岔梁不同位置時的剛度不同而造成道岔梁的反力變化而引起的振動及疊加的振動。在磁浮列車以速度80km/h通過26.5m道岔過程中，并聯阻尼的粘阻系數分別為c=0N.s/m、c=1×105N.s/m、c=2×105N.s/m、c=3×105N.s/m，此時道岔梁的最大應變分別為1.91mm，1.53mm，1.35mm，1.22mm。由于道岔梁臨界阻尼很大，實際情況都是欠阻尼狀態，所以在并聯阻尼器后，道岔梁最大應變有明顯減小，并聯的阻尼越大道岔梁振動越小。在并聯c=3×105N.s/m阻尼后，列車過岔時道岔梁最大應變從無阻尼的1.91mm減小到了1.22mm，不僅小于危險值，滿足結構安全要求，而且道岔梁更小的應變可以減少車身振動，大大提高乘客的舒適度，安全余量更大，安全系數也更高。

4 結語

1）基于中低速磁浮道岔的承載結構特征，本文基于最小二乘曲線回歸方法，通過計算道岔梁縱向多點應變建立道岔梁縱向等效剛度曲線，并采用分段函數擬合，可以提高擬合精度，然后采用建立動力學微分方程的方法建立車岔耦合振動模型，并采用MATLAB進行仿真。

2）對中低速磁浮道岔進行耦合振動分析，得到列車以80km/h，60km/h，40km/h速度通過道岔時無阻尼道岔梁的最大應變分別為1.91mm，1.59mm，1.23mm，相對于磁浮道岔整體尺寸而言較小，小于危險值。但道岔的變形將影響懸浮電磁鐵的控制系統，從而增大車體的振動，影響車體平穩性。

3）對中低速磁浮道岔并聯阻尼器，并建立并聯阻尼器后新的動力學方程，使用同樣的方法進行動力學仿真，得到列車過岔時有阻尼道岔梁應變曲線圖。由圖6可知，在并聯阻尼器后，道岔梁最大應變有明顯減小，在并聯c=3×105N.s/m阻尼后，列車過岔時道岔梁最大應變從1.91mm減小到了1.22mm。道岔梁更小的應變可以減少車身振動，大大提高乘客的舒適度。同時安全余量更大，安全系數也更高。