具有加權特性的彈性網絡聚類算法研究

衣俊艷，吳博雅，雍巧玲

1.北京建筑大學 電氣與信息工程學院，北京100044

2.喀什大學 計算機科學與技術學院，新疆 喀什844000

1 引言

聚類是目前處理數據的重要手段之一，已廣泛應用于諸如生物學[1-2]、圖像處理[3]、金融分析[4-5]等學科領域。聚類是根據一組定義，將一組對象劃分為多個集群的過程，其目的是使同一集群中的對象比不同集群中的對象彼此間更加相似[6]。與監督學習相比，聚類算法通常屬于無監督學習范疇，這也增加了數據聚類的難度。聚類分析技術不僅可以挖掘數據之間的內在聯系，揭示數據的分布特性，還可以作為數據的一種預處理方式，便于后續的數據分析任務[7]。

傳統的聚類算法可以分為五類：基于劃分的聚類、基于網格的聚類、基于層次的聚類、基于密度的聚類、基于模型的聚類。近年來出現了很多新的聚類算法，如基于粒度的聚類算法、基于熵的聚類算法、不確定聚類算法、譜聚類算法、核聚類算法等[8-9]。雖然目前已經有很多關于聚類的算法，但這些算法仍存在以下缺點：可伸縮性差；容易受到噪聲點、離群值等因素的影響；無法自動確定簇數；無法聚類非線性可分離數據集；多維空間聚類質量變差等[10]。

基于劃分的聚類算法如k-means、k-medoids等，其中k-means算法[11-13]具有簡單、高效等優點，但其由于對噪聲點及數據輸入順序的敏感性導致算法結果不穩定的問題是不容忽視的。k-medoids[14]雖然針對該問題進行了改進，但仍未徹底解決。此外，基于劃分的聚類算法大多不能很好地處理具有非凸特性的數據集。基于網格的聚類算法如STING（STatistical INformation Gridbased method）[15]、CLIQUE（Clustering in Quest）[16]等，擅長解決高維大型的數據集，但其求解質量有待提高。基于層次的聚類算法如CURE[17]，能以較低的時間復雜度解決大型數據集，但也存在聚類結果不穩定、聚類質量不高等問題。基于密度的聚類算法如DBSCAN（Density-Based Spatial Clustering of Applications with Noise）[18]、MeanShift[19]等，可以發現數據集中任意形狀的集群，可以排除噪聲的干擾，但不能很好地解決高維問題。基于模型的聚類算法如COBWEB、SOM 等，其中典型的統計學方法COBWEB[20]的算法簡單，能夠快速處理數量級大的數據集，但無法很好地處理多維數據集。典型的神經網絡方法SOM（Self-Organizing Map）[21]，能夠很好地處理高維數據，不受噪聲點的影響，但該算法存在不能保證網絡全局收斂等問題。

由SOM網絡延伸出來的彈性網絡算法（Elastic Net Method）在1987 年被Durbin 和Willshaw 提出[22]，該方法提出伊始被用來解決具有NPC計算復雜性的旅行商問題（Traveling Salesman Problem，TSP）。在沒有先驗知識的條件下進行聚類，一種有效的方法是設定一個聚類的目標函數，求解該函數的最小值，從而獲得具有最佳分布函數的聚類方案。彈性網絡非常適合求解這類問題，可以針對目標函數自動求解，不需要其他人工指導訓練，且保證網絡系統全局收斂。

熵最初是物理學中對系統混亂程度的一種度量，后有科學家從數學角度提出信息熵的概念。1957 年統計物理學家Jaynes提出極大熵原理后，該原理被廣泛應用于許多學科領域中。該原理認為，在掌握部分信息的情況下對分布形狀做出判斷，應該選擇符合約束條件且熵值取得最大的概率分布，任何其他的選擇都意味著人為添加了其他的約束條件，而這些約束或假設是無法根據現有的知識給出的。此外，Jaynes 還指出，在物理學中一些重要的概率分布均是在一定約束條件下滿足極大熵原理的概率分布[23-24]。更為重要的是，極大熵原理滿足第一原理和一致性要求，即極大熵原理利用最少的信息，獲得最超然（Maximally Noncommittal）的解，并且求得的解與求解步驟無關[25-26]。

本文結合極大熵原理、模擬退火思想[27]，應用彈性網絡的求解模式，提出一種新的聚類算法。該算法重新構造與數據點、聚類中心關聯的代價函數，并考慮了各特征屬性對聚類不同程度的重要性等因素，提出一種具有加權特性的彈性網絡聚類算法（Weighting of Elastic Net for Clustering，WENC）。

2 彈性網絡

彈性網絡算法的基本原理是在多元空間中描述各城市點，在城市點構成的空間內生成一個含有彈性節點（Elastic Points）的以數據集重心為中心的封閉圓環，該圓環稱為彈性帶（Rubber Band）。隨著網絡不斷地迭代，彈性帶發生形變，彈性節點的位置不斷變化，不斷向城市點靠近，直到所有的城市點被彈性節點覆蓋，網絡達到穩定狀態，即認為獲得該TSP問題的近似解。在迭代過程中，彈性網絡通過兩種力來牽引彈性節點的移動：一種力是與彈性節點i 相鄰的城市點對彈性節點i的吸引力，使得彈性節點i 逐漸向城市點靠近；一種力是與彈性節點i 相鄰的彈性節點對彈性節點i 的張力，迫使彈性節點之間的距離最短。

假設給定數據集X={x1,x2,…,xn} 含有n 個城市點，在該空間內初始化含有m 個彈性節點的彈性帶Y={y1,y2,…,ym}，一般n ＜m 。隨著網絡的迭代，彈性網絡追蹤能量函數式（1）的極小值：

其中，K 逐漸減小，與退火算法（Deterministic Annealing Method）中的溫度對應。參數α、β 分別決定城市對彈性節點的力和彈性點間的力的影響程度。彈性節點每次迭代需要的位移量為：

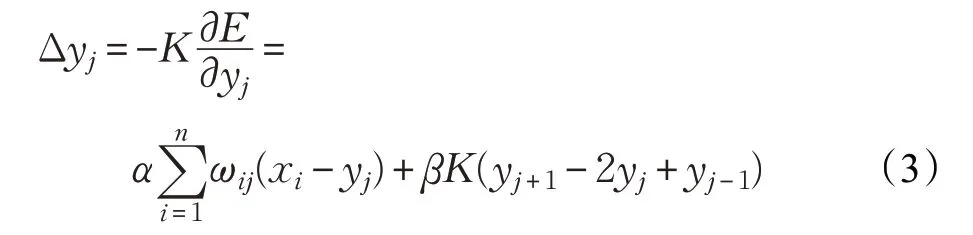
其中，ωij代表城市點i 在路徑上對彈性節點j 的影響程度，其描述如式（4）所示。

當K →0 時，能量函數獲得局部最小，此時每個城市點至少匹配到一個彈性節點。當城市點有且只匹配到一個彈性節點時，認為網絡獲得最優解決方案。

3 具有加權特性的彈性網絡聚類算法

傳統的聚類分析算法通常將數據所有的特征屬性按照相同的重要程度進行聚類，然而在多維數據聚類中，所有的特征屬性對聚類的重要程度并不完全相同，有些特征屬性甚至可能是噪聲特征，進而影響聚類的結果[7，28]。本文根據彈性網絡的特點，設計了一種加權方式，使其能夠在多維數據集中更好地進行聚類。彈性網絡算法雖然非常適合求解具有目標函數的問題，但并不能直接用于解決聚類問題，本文將詳細介紹具有加權特性的彈性網絡聚類算法。首先，根據聚類的目標確定初始權值的方法。然后，引入加權思想，針對聚類問題構建基于數據點與聚類中心間距離平方的能量函數，并運用極大熵原理給出數據點的概率分布。然后，針對算法的彈性帶初始化、能量函數、權值等問題進行詳細分析。最后，給出算法的執行過程。

3.1 算法原理及分析

假設在多元空間中，給定一含有n 個數據點的數據集X={X1,X2,…,Xn}，每個數據點均具有m 個特征屬性Xi=(xi,1,xi,2,…,xi,m)，目標是將該數據集分為k 簇。初始化一條含有k 個彈性節點的彈性帶Y={Y1,Y2,…,Ym}，每個彈性節點均具有m 個特征屬性Yj=(yj,1,yj,2,…,yj,m)，每個特征屬性上所加的權值為U=(u1,u2,…,um)。考慮到各特征屬性在聚類過程中的影響各不相同，因此需要確定各特征屬性的權值。本文首先介紹一種確定特征屬性權值的方法。

在彈性網絡聚類算法（Elastic Net for Clustering，ENC）中，所有特征屬性對聚類過程的影響程度相同，此時相當于各特征屬性的權值均為1，即U=(u1,u2,…,um)=(1,1,…,1)，相當于網絡不加權。如果某一維對聚類的影響度不那么重要，其存在甚至影響聚類結果變差，但若直接刪掉該特征屬性，會破壞數據集原本的結構。因此需要對該特征屬性的權值進行處理，一方面減少其對聚類結果的影響，另一方面保留了原始數據集的結構特性。

聚類的目的是根據數據的內部結構，將數據劃分成一些集群，每個集群中的對象盡可能相同，不同集群中的對象盡可能不同，由此可以判定，當某特征屬性較為離散時，該特征屬性不利于聚類。本文首先利用式（5）對所有特征屬性的離散程度進行判斷，其中xˉl為第l 個特征屬性的所有數據點的均值。然后根據式（6）計算閾值：當某特征屬性的離散程度超過該閾值時，根據式（7）計算該特征屬性的權值，其中δ 為權值系數，根據數據集的特征選取；當某特征屬性的離散程度未超過該閾值時，該特征屬性的權值為1。

聚類的目標是使類內對象盡可能相似而類間對象盡可能不同，即數據點到各簇中心的距離和最小，根據該目標可以發現衡量聚類質量的一個重要標準SED（Sum of Euclidean Distance）值與此概念一致，如式（8）所示：

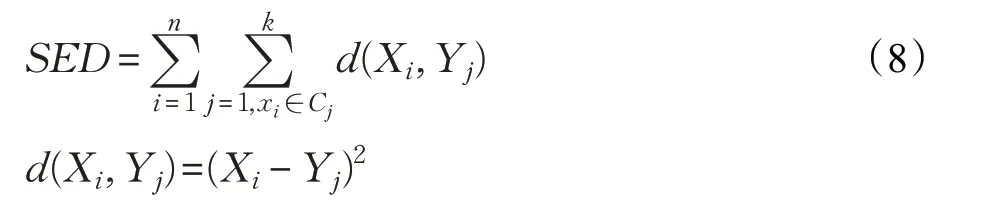
其中，Xi為第i 個數據點，Yj為第j 個聚類中心點，Cj表示聚類產生的以Yj為聚類中心的集群。

本文針對聚類問題，直接將各簇之間的距離平方和設置為能量函數，如式（9）所示。在該能量函數的作用下，所有數據點對每個神經元都具有吸引力，神經元在該力的作用下進行移動。隨著網絡的運行，能量函數值不斷下降，神經元沿著使SED值最小的方向移動，當能量函數達到全局極小，SED 值也達到最小值，從而求得該聚類問題的最優解或近似最優解。此外，傳統的聚類分析算法通常將數據所有的特征屬性按照相同的重要程度進行聚類，然而在多維數據聚類中，所有的特征屬性對聚類的重要程度并不完全相同，有些特征屬性甚至可能是噪聲特征，進而影響聚類的結果。因此，本文引入加權思想，將能量函數定義為式（9），總的能量函數定義為式（10）。

其中，Pi,j為數據點xi屬于某一簇Cj的概率分布，在沒有先驗知識的情況下，不能隨便確定其具體模式。本文采用極大熵原理來確定Pi,j的概率分布。

將聚類模型視作物理系統模型，對給定的彈性節點y1,y2,…,yk定義熵函數H ，如式（11）所示。

在本文的能量函數中，除考慮數據點與彈性節點之間的作用外，還考慮了彈性節點之間的交互作用，如式（12）所示。

其中，常數λ 為彈性系數。

綜上，與能量函數相應的亥姆霍茲自由能（Helmholtz Free Energy）如式（13）所示[29-30]，其中Z 為總的配分方程。

本文將數據集中的數據點描述為多變量空間中的數據點，在沒有先驗知識，也不對數據集做任何假設約束的情況下，利用極大熵原理來確定彈性節點與數據點之間的概率分布。在該算法中彈性網絡節點的位置代表聚類中心，而每個數據點隸屬于該簇的概率符合高斯概率分布，由式（14）給出[26，29]。

其中，Zi為配分方程：

其中，參數β 與溫度K 成反比，即β 越小溫度越高，當β=0 時，每個數據點屬于每簇的概率相同；隨著β 不斷增加，當β →∞時，每個數據點以1 的概率僅屬于一個簇。由于每個數據點屬于不同簇的概率是不同的，因而總的配分方程為：

在網絡不斷迭代的過程中，彈性節點在數據點的吸引力和相鄰彈性節點間的張力的作用下不斷移動位置，每次迭代需要移動的量由式（17）計算得到：

其中，常數Δτ 為每次迭代的步長，選擇合適的Δτ 能夠使網絡進行充分的運行。

3.1.1 彈性帶初始化算法分析

由于k-means、k-medoids 算法隨機確定初始的聚類中心點，每次運算的結果受到聚類中心點初始位置的影響，使得算法針對同一問題每次運算的結果不唯一。而本文提出的WENC 算法通過設置彈性帶的方式，對神經元位置進行初始化，使算法針對同一問題求解結果唯一。WENC算法初始化彈性帶的方法描述如下：

其中，xi,l表示第i 個數據點的第l 個特征屬性。

（2）利用式（19）計算初始彈性帶的半徑R：

（3）初始化彈性帶為以重心Xˉ為圓心，以R 為半徑的封閉圓環，在本算法中選擇前兩維初始彈性帶，k 個彈性節點均勻分布在彈性帶上。

該方法綜合考慮了所有數據樣本的位置，根據所有數據點的坐標計算該數據集的重心Xˉ，繼而確定神經元的初始位置。該方法可以根據不同的數據分布情況動態調節彈性網絡神經元的初始位置，以適應不同問題的需要。在使用該方法確定彈性網絡初始神經元位置后，針對同一聚類問題，WENC網絡運行結果唯一。

為驗證WENC算法與k-means、k-medoids算法聚類結果的穩定性，本文做了大量實驗，此處選取含有800、1 000、3 000、5 000 個數據點的4 組數據集，分別利用k-means、k-medoids、WENC 算法多次運行，結果對比如圖1所示。

從圖1 中可以發現，針對同一問題，k -means、k -medoids算法多次運行結果不唯一，而WENC 算法多次運行的結果唯一。在20 次的運行中，WENC 算法的結果均優于k-means、k-medoids算法。在這4組實驗中，WENC 算法求解的SED 值分別比k -means 算法求解的SED 平均值減少5.22%、5.26%、3.83%、5.00%，比k -medoids 算法求解的SED 平均值減少6.55%、5.15%、8.25%、6.15%。因此在本文后續實驗中，利用k-means、k-medoids算法對每組數據集分別進行20次測試，取結果的平均值進行比較。

3.1.2 能量函數分析

為評估WENC 算法自由能函數的作用，本文選取一組含有1 000個數據點的數據集來展示在聚類過程中自由能函數及其對應的SED 值隨迭代的演化過程，如圖2 所示。圖2（a）為WENC 算法的自由能函數隨迭代的變化過程，圖2（b）為在聚類過程中，每次迭代自由能函數變化時對應的SED值。由圖2可知，隨著迭代次數的增加，自由能函數值逐漸降低，對應的SED值逐漸減少。在此過程中，網絡會陷入局部極小值，因此自由能函數值與SED 值均出現一個較為穩定的狀態。隨著迭代繼續進行，在能量函數的作用下，網絡具有針對該聚類問題的自適應、自學習能力，從而能夠主動跳出局部極小，尋找到更接近全局最小的解。

圖1 k-means、k-medoids、WENC算法多次運行結果對比圖

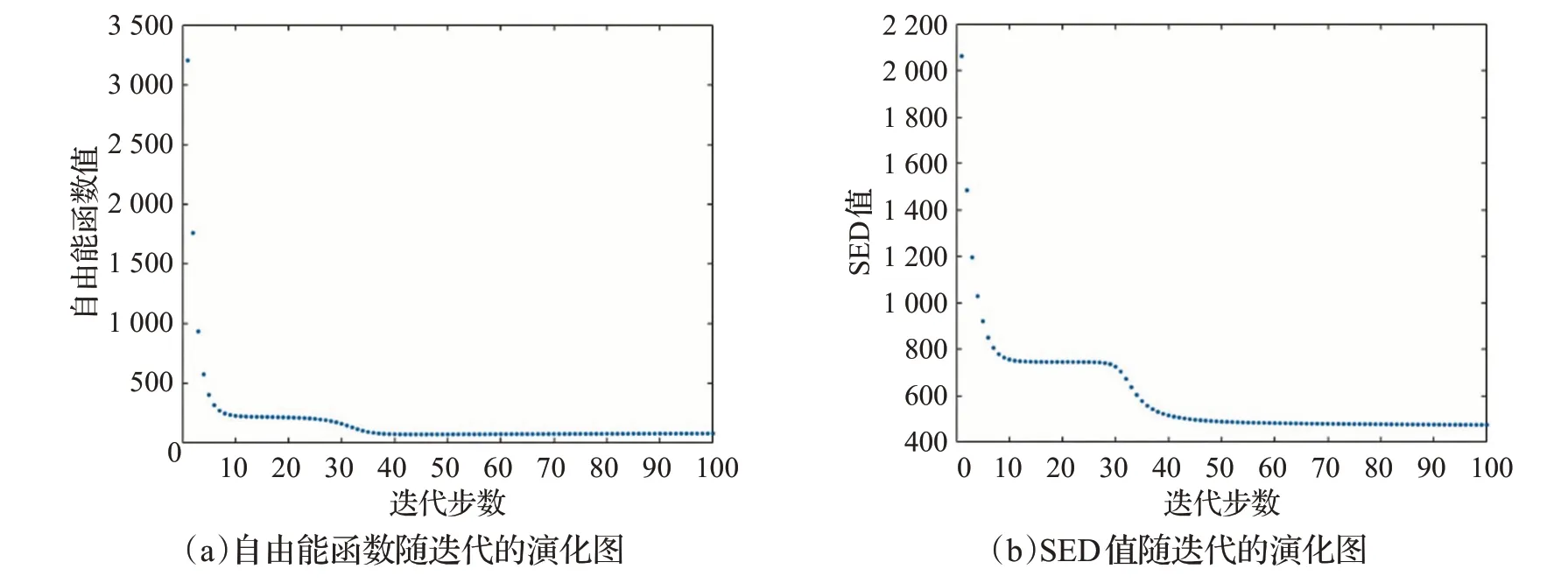
圖2 WENC算法自由能函數及對應SED值隨迭代的演化圖

本文所提出的能量函數，除考慮了數據點與彈性節點之間的作用外，還考慮了彈性節點之間的交互作用：在能量函數中增加了式（12），即增加了相鄰神經元之間的吸引力。這有助于保持網絡拓撲結構，保證網絡運行和求解的穩定性。通常情況下，由于彈性網絡神經元節點數目等于聚類數目，大量數據點與少量彈性節點交互，因此能量函數中有關相鄰神經元相互作用的計算量增量有限。為驗證考慮彈性節點間作用力對網絡運算的影響，本文選取一組含有500 個數據點的數據集，分別使用未考慮彈性節點間影響力的NENC（Non-node Elastic Net of Clustering）算法和本文提出的考慮彈性節點間影響力的WENC算法迭代100次，SED值隨迭代的變化以及運行所用的時間對比如圖3所示。從圖3可以發現：在聚類結果上，WENC 算法和NENC 算法每次迭代在SED值上的差別并不明顯；在運行時間上，兩種算法均迭代100次，WENC算法比NENC算法運行時間僅多了0.02 s。可見彈性節點之間的交互作用對算法運算的成本影響較小，因此在計算成本方面神經元之間的交互作用可以視為擾動。

圖3 WENC、NENC算法的SED值變化及運行時間對比圖

相鄰神經元之間的相互作用，在網絡的運行求解過程中起到重要作用，它有助于保持網絡的拓撲結構，并保證網絡求解的穩定性和唯一性。圖4 為針對同一四維含有1 000 個數據點的聚類問題，多次運行WENC算法和NENC 算法的結果對比。由圖4 可見，未添加彈性節點之間相互作用的NENC 算法每次運行的結果不穩定，而WENC 算法則在多次計算中取得穩定的唯一解。因此，考慮相鄰神經元間的相互作用是非常必要的。

圖4 WENC算法與NENC算法多次運行的結果對比圖

通過上述理論分析和實驗驗證，本文提出的WENC算法在能量函數公式（13）的作用下，網絡中的每一個彈性節點yj在數據點的吸引力和相鄰彈性節點間的張力作用下不斷移動位置。如圖5 所示為某時刻單個彈性節點yj與數據點xi之間的力的作用圖，F1為相鄰彈性節點對彈性節點yj的張力之和，F2為數據點xi對彈性節點yj的吸引力。

圖5 某時刻單個神經元的受力圖

在神經網絡中，一般通過觀察單神經元模型來驗證神經網絡的性能及改進方法對網絡的影響。但由于彈性網絡中彈性節點是在相鄰彈性節點和數據點共同作用下進行移動，因此通過單神經元模型進行觀察的方法并不適用于彈性網絡。本文選取只含有3 個神經元的簡單網絡模型進行實驗，通過選取單個典型神經元作為觀察點來驗證加權后對速度的影響。單個彈性節點每次迭代移動的量隨著迭代次數的增加逐漸趨于0，當彈性節點的移動量連續10 次小于0.001 時，網絡停止運行，此時彈性節點的位置即為聚類中心點的位置。

基于以上理論分析，本文對網絡迭代速度進行了實驗，得到如圖6所示結果。圖6（a）、（b）分別為彈性節點橫縱坐標每次迭代的位移量的變化過程，其中WENC為本文提出的加權彈性網絡聚類算法，ENC為未進行加權的彈性網絡聚類算法。從圖6可以看出，本文提出的WENC 算法迭代了26 次即得到聚類結果，運行時間為0.528 s；ENC 算法則迭代了28 次，運行時間為0.544 s。此外，本文在不同數據集下還進行了網絡聚類所需迭代次數的對比，結果如圖7所示。從圖7可以發現，在不同大小的數據集下，WENC 算法的迭代次數均少于ENC算法。因此，改進后的加權彈性網絡WENC 能夠更快地找到聚類中心，比不加權的ENC算法的性能更高。

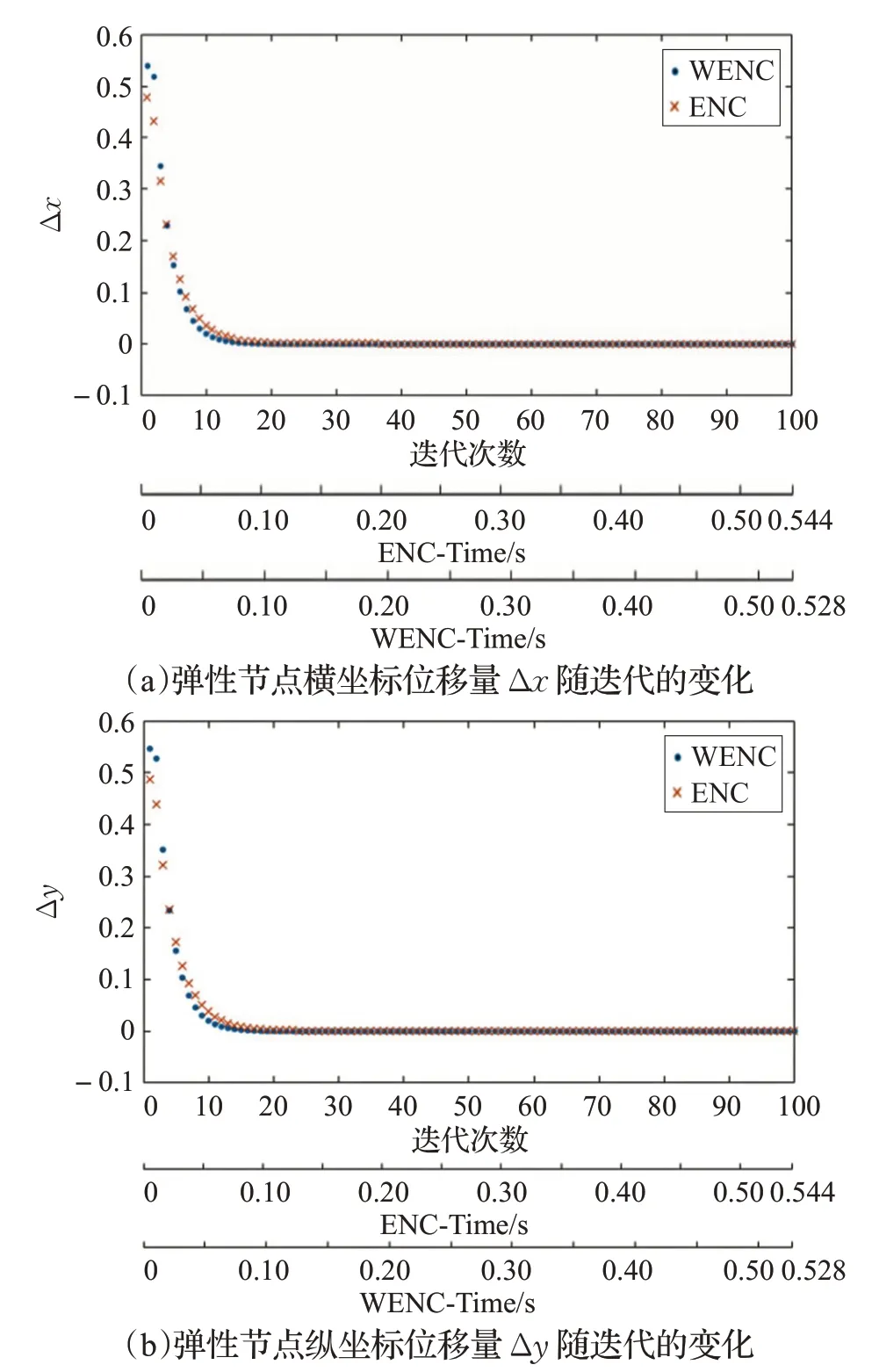
圖6 彈性節點橫縱坐標位移量的變化過程

圖7 不同大小數據集的迭代次數對比圖

3.1.3 權值設置分析

為驗證加權對網絡的影響和意義，本文選取一組隨機數據集將WENC算法與其他常用聚類算法進行實驗比對。該數據集共含有3 個特征屬性，180 個樣本點。在本實驗中，利用SED 值對聚類的結果進行評價，SED值越小，代表聚類的質量越高。

首先根據式（5）分別計算各特征屬性的離散程度，結果如表1所示。然后利用式（6）計算得閾值V=3.40，由此判斷僅第3個特征屬性需要計算新的權值，其余特征屬性權值仍為1。

表1 三維隨機數據集所有特征屬性的離散程度

根據該數據集的結構，設置參數δ 為0.96，計算得第3 個特征屬性的權值為0.5，本文提出的WENC算法與不加權彈性網絡ENC、k -means、k -medoids、MeanShift 聚類算法的結果對比如表2 所示。其中，k -means、k -medoids 算法對初始中心點的位置非常敏感。每種算法分別進行20 次測試，取所有SED 值的平均值作為最終結果進行比較。

表2 三維180個樣本點的數據集各聚類算法結果對比

由表2的數據對比可知，對數據集進行加權之后網絡聚類效果更好，與k-means、k-medoids、MeanShift以及不加權的ENC 算法相比，SED 值分別提高8.5%、6.6%、11.4%、4.1%。 k -means、k -medoids、MeanShift、ENC以及WENC各算法結果的平面圖分別如圖8～圖12所示，其中圖（a）、（b）、（c）分別顯示了數據集中各屬性維度之間的關系。

圖8 k-means算法的聚類結果

圖9 k-medoids算法的聚類結果

圖10 MeanShift算法的聚類結果

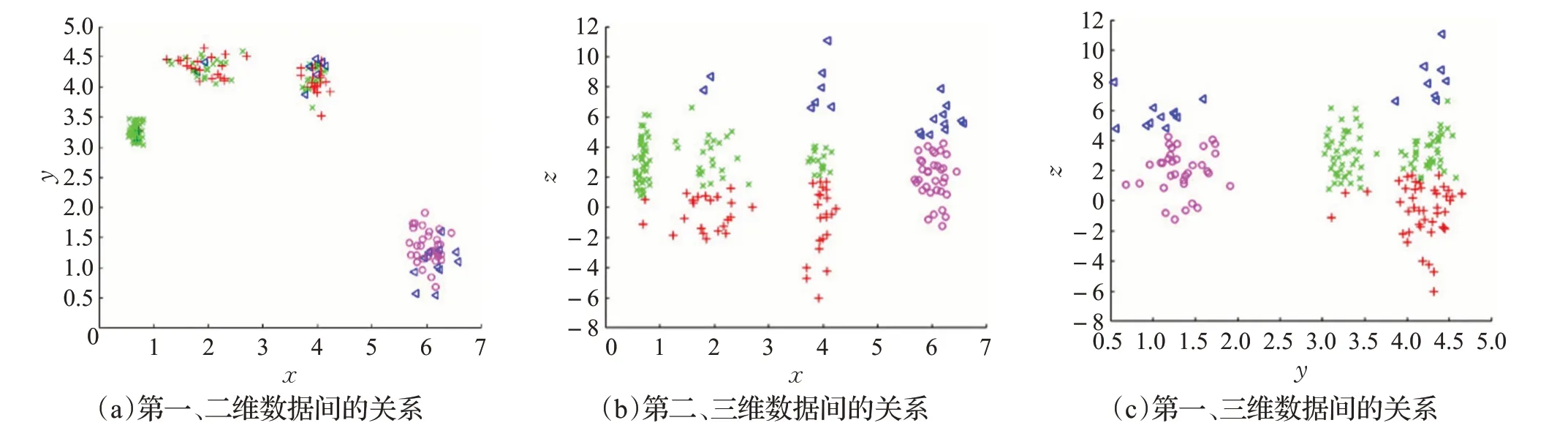
圖11 ENC算法的聚類結果

圖12 WENC算法的聚類結果

對比圖8～圖12 可以觀察出，該數據集中有一個特征屬性較為離散，不利于聚類過程的進行。k -means、k -medoids、MeanShift、ENC 算法在聚類過程中均受到該特征屬性的干擾，在圖8～11（a）中，各簇的劃分情況并不理想。而WENC算法利用權值降低該特征屬性對聚類過程的影響，圖12（a）中各簇的劃分較為清晰，WENC算法的聚類結果更優。

由此可知，在進行聚類時，不同的特征屬性對聚類過程的影響不同，將不利于聚類的特征屬性的影響度降低后，可以提高聚類結果的質量。

3.2 算法描述

本文在彈性網絡的基礎上，引入機械函數和加權思想，構造新的能量函數，并利用極大熵原理確定數據點的概率分布，使算法更具有普適性。通過權值確定的策略，減小不利因素對聚類的影響，再計算自由能函數，當彈性節點每次迭代的位移量連續10次小于0.001時，網絡停止運行并獲得最后的聚類方案。該方法不僅提高了聚類質量，網絡整體也比其他算法更加穩定。WENC算法的具體步驟如下：

（1）給定一個含有n 個數據點的數據集X={X1,X2,…,Xn} ，每個數據點均具有m 個特征屬性Xi=(xi,1,xi,2,…,xi,m)。根據式（5）、式（6）分別計算每個特征屬性的離散程度Gl和閾值V 。

（2）判斷Gl是否大于閾值V ：若是，則根據式（7）計算該特征屬性的權值ul；若否，則初始化該特征屬性的權值ul=1。

（3）在數據空間內初始化一個含有k 個彈性節點的彈性帶Y={Y1,Y2,…,Ym}，每個彈性節點均具有m 個特征屬性Yj=(yj,1,yj,2,…,yj,m)。彈性帶是以數據集的重心Xˉ為中心，R 為半徑的封閉圓環，Xˉ、R 分別根據式（18）、式（19）計算獲得，彈性節點均勻分布在彈性帶上。

（4）根據式（13）計算數據點及相鄰節點間的總能量，并由推導出的式（17）計算每次迭代彈性節點在每個特征維度上移動的距離Δyj,l。

（5）重復步驟（4），當彈性節點的移動量連續10 次小于0.001時，網絡停止運行，此時彈性節點的位置即為各集群的中心點，即獲得各簇的聚類中心點。

（6）計算數據點到各彈性節點的距離Di,j，并將數據點分配至距離該點最近的彈性節點，獲得最終的聚類方案，完成聚類。Di,j如式（20）所示：

4 實驗仿真

彈性網絡具有非常好的幾何特性，能夠有效地解決固定目標函數求解極小值的問題，因此基于彈性網絡的聚類算法雖然能夠很好地對數據集進行聚類，但只適用于數值型數據集，非數值型數據集必須轉換為數值型數據集后才能夠進行聚類運算。

為驗證WENC 算法是否能夠有效提高聚類質量，本文采用了大量的隨機數據集和真實數據集對其進行實驗仿真。由于隨機數據集沒有標簽，隨機數據集的實驗結果通過聚類標準SED 值來評價。真實數據集的實驗結果通過SED 值和Accuracy 來評價。Accuracy 的計算方法如式（21）所示。

其中，ai為被正確分類的數據點的個數，N 為數據集中所有數據點的個數。

4.1 隨機數據集

隨機數據集生成的方法類似文獻[31]，由Matlab程序生成。為使實驗更具普適性，本文合成了含有不同特征屬性、不同數量級的數據集。WENC算法中參數設置為β=1,Δτ=0.001,λ=0.5。每次實驗的彈性帶以實驗數據的重心Xˉ為中心，半徑R 通過式（19）確定。為顯示WENC算法的優勢，每組實驗均與k-means、k-medoids、MeanShift以及未加權的彈性網絡聚類算法ENC的結果進行對比。由于k-means、k-medoids 算法對初始中心點的位置非常敏感，分別對每組數據集進行20次測試，取結果的平均值進行比較。

為驗證網絡增加權值的有效性，本文首先選取了具有60、300、1 000個數據點的數據集，表3列出了各組數據集詳細的聚類結果。

由表3 可以得到五種算法在不同維度下平均SED值的比較結果：對含有60、300、1 000個數據點的隨機數據集，WENC算法求解的SED值比k-means算法分別減少7.51%、6.12%、1.82%，比k -medoids 算法分別減少8.93%、10.42%、7.57%，比MeanShift 算法分別減少8.67%、24.29%、19.53%，比ENC 算法分別減少2.65%、3.33%、7.99%。此外WENC網絡運行多次結果不變，與k -means、k -medoids 算法相比，結果非常穩定，因此本文提出的WENC算法在解決聚類問題時不需要多次運行。綜上，對不同的多維隨機數據集，WENC 算法均可獲得比k-means、k-medoids、MeanShift、ENC算法更好的聚類結果，驗證了加權的有效性。此外加權提高了網絡的求解速度，速度對比如圖6所示。

為驗證WENC 算法處理大規模數據集的能力，本文還對具有3 000、6 000、10 000個數據點，分為3簇、10簇的數據集進行實驗。具體實驗結果如表4所示。

由表4 可以得到五種算法在不同維度下的平均SED 值比較結果：對含有3 000、6 000、10 000 個數據點的隨機數據集，WENC算法求解的SED值比k-means算法分別減少1.43%、0.87%、2.03%，比k-medoids 算法分別減少6.29%、5.15%、7.12%，比MeanShift 算法分別減少25.46%、20.98%、20.82%，比ENC 算法分別減少8.91%、3.55%、0.41%。此外WENC 網絡運行多次結果不變，與k-means、k-medoids算法相比，結果非常穩定，分析對比如圖1所示。綜上，對不同的多維隨機數據集，WENC 算法在處理大規模數據集方面均可獲得比k -means、k-medoids、MeanShift、ENC算法更好的聚類結果。

表3 隨機數據集聚類結果對比

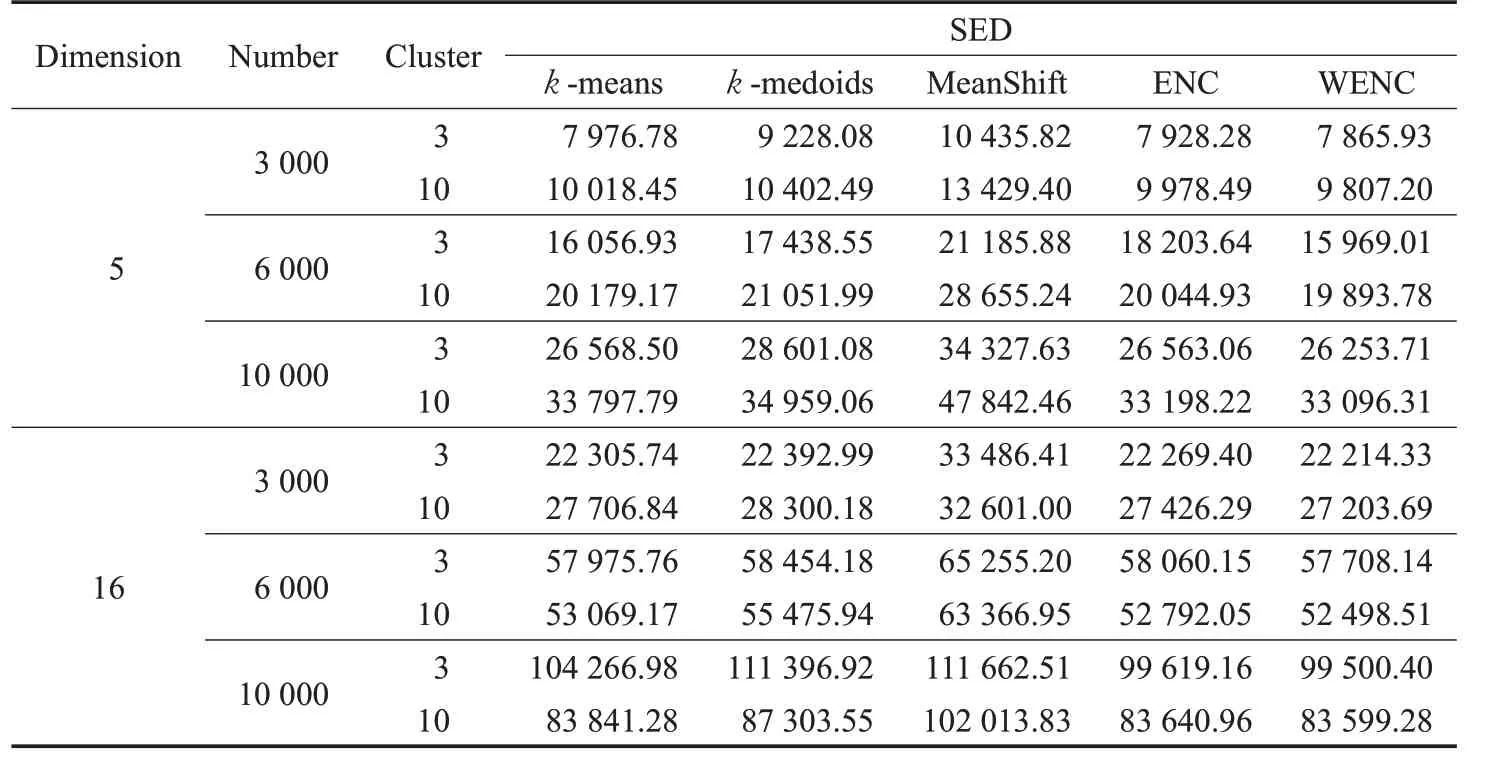
表4 大規模隨機數據集聚類結果對比

表5 真實數據集聚類結果對比

4.2 真實數據集

真實數據集是從標準庫UCI內獲取的，與k-means、k-medoids、MeanShift算法進行了對比實驗。本文選取Zoo、Seeds、Iris、Wine、Handwritten等數據集進行運算測試。其中Zoo 包含101 個數據樣本，16 個特征屬性，目標劃分為7 簇；Seeds 包含210 個數據樣本，7 個特征屬性，目標劃分為3 簇；Iris 包含150 個數據樣本，4 個特征屬性，目標劃分為3簇；Wine包含178個數據樣本，13個特征屬性，目標劃分為3 簇；Handwritten Digits（為方便記錄，表中記為Hand）包含10 992 個數據樣本，16 個特征屬性，目標劃分為10 簇。該實驗使用與隨機數據集實驗相同的方法對聚類結果進行評估，并增加Accuracy聚類標準來多方面評估聚類結果。實驗的詳細結果如表5所示。

通過對比表5的數據結果可知，WENC算法在真實數據集中的聚類結果，與k-means 算法對比，SED 值分別降低20.68%、22.29%、7.54%、13.06%、9.65%，Accuracy分別提高19.70%、31.88%、18.33%、30.43%、8.82%；與k -medoids 算法結果對比，SED 值分別降低16.88%、21.25%、5.95%、13.06%、5.64%，Accuracy 分別提高16.18%、28.17%、9.23%、18.42%、17.46%；與MeanShift算法結果對比，SED值分別降低4.13%、2.21%、17.17%、0.69%、10.22%，Accuracy 分別提高9.72%、2.25%、10.94%、2.27%、25.42%。實驗結果表明，WENC算法不僅提高了聚類質量，還優化了Accuracy，聚類結果得到有效改善。

由此分析，本文提出的WENC 算法無論對低維還是高維數據集的聚類能力均優于k-means、k-medoids、MeanShift 等傳統算法。此外，WENC 算法在排除噪聲因素干擾、穩定聚類的同時，保證了整個網絡收斂。

5 結束語

本文針對聚類算法中存在的聚類結果易受噪聲干擾、多維空間聚類質量不佳等問題，提出了一種具有加權特性的彈性網絡聚類算法（WENC）。與傳統聚類算法相比，本文選擇適合求解固定目標函數極小問題的彈性網絡模型。由于原始彈性網絡不能直接用于解決聚類問題，本文在彈性網絡基礎上考慮到不同特征屬性對聚類的重要程度不同，通過對數據集中某些影響聚類結果的特征屬性進行加權，達到削弱這些特征屬性在聚類過程中對網絡影響的目的。基于以上原理，重新構建模型的能量函數，并結合極大熵原理確定數據集的概率分布。設置新的彈性網絡目標函數，以達到聚類的目的。該算法中彈性網絡初始彈性節點的數量與目標劃分簇數相等，在網絡利用模擬退火思想，不斷給系統“降溫”達到能量函數最小值時，彈性節點的位置即為聚類各簇中心點的位置。此外，由于更改了彈性節點初始化的個數，使得彈性網絡針對聚類問題可以求解含有近一萬個樣本點的多維數據集，顯著提高了求解問題的規模。最后，在不同維度、不同數量級的隨機數據集以及UCI 真實數據集上進行了實驗，并分別利用聚類內部評價標準SED 值和聚類外部評價標準Accuracy 對聚類結果進行評估，結果表明，WENC 算法能夠對高維數據集穩定地提供更好的聚類方案。