應用大數據優化高中數學課堂教學效果的復習課創課設計

王菊香 張虎臣

【摘要】高中數學復習課是課堂里出現頻率很高的一種課型， 優化高中數學課堂教學的效果是非常有必要的。教育大數據走進了課堂， 幫助老師全面深入的分析了學情、考情， 這樣老師就可以在復習課的內容上進行精準定位， 設計出精準的復習課教案， 并實施精準教學， 從而達到優化課堂教學的效果。

【關鍵詞】教育大數據? ?復習課? ?精準教學? ?優化

【中圖分類號】G633.6

【文獻標識碼】A

【文章編號】1992-7711（2020）31-225-01

學習目標：能解決直線同側兩個定點與直線上一點距離的和的最小值問題， 并能給出嚴謹的證明。

核心素養目標： 數學建模， 數學抽象， 邏輯推理， 直觀想象和數學運算。

重點： 掌握直線、橢圓、拋物線同側兩個定點（其中一個定點為圓心或焦點）與曲線上一點距離和的最值問題， 并能給出嚴謹的證明。

學習過程：

路徑最值的問題1：直線型河流

如圖1所示，電工師傅要從發電房A處拉導線到河岸邊（直線）安裝一盞燈P后，再到倉庫F處， 路燈P點應選在河岸的哪點處用的導線最短（|PA|+|PF|的和最小）？

解答： 作A點關于直線l的對稱點A'， 連接A'F交l于點， 所以此點為所求， 記為Pmin.

證明： 連接AA'， PminA，PminF

因為點P在線段AA'的垂直平分線l上， 所以|PA|=|PA'|.

在ΔA'FP中， 由任意兩邊之和大于第三邊， 得|PA'|+|PF|>|A'F|， 所以|PA|+|PF|=|PA'|+|PF|>|A'F|

當且僅當A'，P，F三點共線時，（|PA|+|PF|）min =（|PA'|+|PF|）min=|A'F|.

點評： 直線同側的兩點通過對稱把其中一點轉移到直線的另一側， 在根據三點共線和兩點之間線段最短， 問題得以解決。

路徑的最值問題2：橢圓型河流

如圖所示2， 電工師傅要從發電房F（橢圓左焦點）處拉導線到河岸邊（橢圓：長軸長為2a）安裝一盞燈P后， 再到倉庫A處， 路燈P點應選在河岸的哪點處用的導線最短或最長（|PF|+|PA|的和最小或最大）？

分析：? 橢圓上動點在橢圓上運動的時候， |PA|+|PF|和的最小或最大時P點的位置。

解答： 取橢圓的另一個焦點F2， 作直線AF2， 交橢圓于兩點，此兩點為所求， 記為Pmin，Pmax.

證明： 因為|PF|=2a-|PF2|，

所以|PA|+|PF|=2a+|PA|-|PF2|

在ΔPAF2中， 由任意兩邊之差的絕對值小于第三邊， 得||PA|-|PF2||<|AF2|， 所以-|AF2|<|PA|-|PF2|<|AF2|，

當且僅當A，P，F2三點共線時，

（|PA|-|PF2| ）min=-|AF2|，

（|PA|-|PF2| ）max=|AF2|，所以

（|PA|+|PF|）min=2a+（|PA|-|PF2|）min

= 2a+（|PminA|-|PminF2|）=2a-|AF2|，

（|PA|+|PF| ）max=2a+（|PA|-|PF2|）max

= 2a+（|PmaxA|-|PmaxF2|）=2a+|AF2|.

點評： 利用橢圓的定義把焦點轉移到另一個焦點， 兩線段之和化成了之差。 在利用三角形任意兩邊之差的絕對值小于第三邊， 解決了此問題。

路徑的最值問題4：拋物線型河流

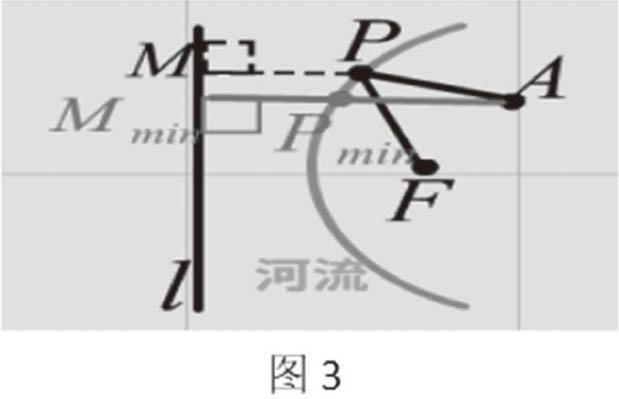
如圖3所示，電工師傅要從發電房F（拋物線焦點）處拉導線到河岸邊（l是拋物線的準線）安裝一盞燈P后，再到倉庫A處，路燈P點應選在河岸的哪點處用的導線最短（|PF|+|PA|的和最小）？

分析：? 拋物線上動點在拋物線上運動的時候，|PA|+|PF| 和的最小時點P的位置。

解答： 過A作準線l的垂線交拋物線于一點，所以此點為? 所求， 記為Pmin.

證明： 由拋物線的定義得|PF|+|PM| ， PM⊥l于M.? 所以|PA|+|PF| =|PA|+|PM| ，當且僅當A，P，M三點共時，（|PA|+|PM|）min=|PminA|+|PminMmin|=|AMmin|.

所以（|PA|+|PM|）min=|AMmin|.

點評： 根據拋物線的定義， 把焦點轉移到準線上， 從而兩定點分布在河流兩側， 利用三點共線解決了此問題。

結語： 在教育大數據時代， 大數據分析平臺給教學提供了很大的輔助功能， 使老師對學生的學情和考情得到充分的掌控， 從而課堂教學設計得以精準定位， 課堂教學效果得以優化。

【參考文獻】

[1]喻文俊. 高中數學課堂中三疑三探教學模式研究[J].? 中國農村教育. 2019（36）

[2]劉妹平.高中數學課堂教學有效提問策略[J]. 科技視界. 2013（31）