質量阻尼比對圓柱體流致振動捕能效率的影響
白旭,韓傳煜,孫海
(江蘇科技大學 船舶與海洋工程學院,江蘇 鎮江 212003; 2.哈爾濱工程大學 航天與建筑工程學院,黑龍江 哈爾濱 150001)
流致振動廣泛地存在于許多工程領域中[1],作為儲量巨大的清潔能源,海流能與風或海浪相比,具有季節性、周期性,其流動狀況高度可預測。但近海岸洋流流速往往較低,導致難以利用傳統方式獲取海洋能量。流致振動捕能技術正在成為可再生能源發電的可行解決方案,需要開展重大的研究、開發和部署計劃,才能在該領域取得真正的產業成功[2]。近年來,許多學者開始研究利用流致振動獲取低流速下海洋動能的發電方式。
流致振動是指流體流經固體時會對固體表面施加交替相間的流體力,使得固體發生往復運動,而固體的往復運動又改變流體流態,進而改變作用于固體表面的流體力[3]。盡管有關流致振動發電的研究并未形成系統的研究體系[4],但仍取得了成果。Belloli等[5]比較了臨界流動狀態下渦激振動與亞臨界振動的特征。Sun Hai等[5-7]研究具有端部彈性約束的剛性振子的流致振動,對幅度響應,頻率響應,能量收集和效率的實驗結果進行了介紹和討論,并使用2個汽缸串聯進行實驗,給出了能量收集和效率的實驗結果、推導出最優功率的包絡。羅竹梅[8]提出了一種結合并列和串列構形的矩形布置四圓柱振動系統,并提出機械耦合的概念描述這種系統的動態特性,將由4個圓柱組成的振動系統整體視為一個質量-彈簧-阻尼系統。Kim等[9]證明了交替提升技術(ALT)轉換器是一種能量吸收裝置,可有效地在速度低至1.0~1.5 m/s的水流中工作,這是目前水車和渦輪機無法達到的速度范圍。燕翔[10]分析了電機參數、機械參數及振子截面參數對三棱柱振動模式、能量利用的影響,明確了三棱柱在流致振動能量利用上的優勢。練繼建等[4]剖析了研究當中存在的各類問題,并對流致振動能量利用的研究方向提出了建議。這些研究集中在物理結構、流速等參數對振動的影響上,尚未存在對振動捕能效果的組合優化的研究。本文工作是研究在現有非理想條件下,所能達到的能量轉化率最大值,即最優捕能效率值。
1 振動能量獲取的數學物理模型
1.1 能量的獲取過程
對于本文所建立的流致振動模型,其運動中產生的可利用能量經歷了2次削弱的過程:1)振動系統獲取流體動能時,有一部分流體動能耗散在振子尾流粒子的碰撞、摩擦中,還有一部分流體未參與做功;2)振動系統獲取的能量會有一部分損失在振動系統機械部分的摩擦中,剩下的部分才是可以加以利用的機械能,也即輸入發電機的能量。能量轉化過程如圖1所示。
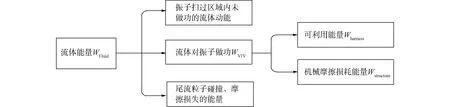
圖1 水流能量的利用流程Fig.1 Flow of water flow energy
1.2 振子物理模型及受力分析
計算采用的振子直徑D=0.1 m,展向長度L=1 m,振子表面光滑,由2支拉壓彈簧連接在支架上,彈簧剛度為K=500 N/m。模擬質量比m*取1.1、1.4、1.7、2.0這4個數值,阻尼比ξ從0.03~0.21每隔0.03取值一次,總計取7個值。對以上28種情況,約化速度從2~12,間隔0.1取值計算。
在流致振動過程中,振子在豎直方向受3個力:即彈簧拉壓力Fspr、結構及水流的阻力Fdamp、流體動壓力FFluid。
如圖2所示,當振子處于平衡位置以下且運動方向向下時,其加速度方向向上。故可以得到等式:
mosca+Fspr+Fdamp=FFluid
(1)
整理得:
(mosc+ma)Y″+(cfluid+cstructure)Y′+KY=
(2)
式中:cFluid為流體附加阻尼;cstructure為振動結構的總阻尼;Γ為離散點渦強度;U為水流的來流速度;D、L為圓柱振子的直徑、長度;ma為振子的附加質量;流體力FFluid根據文獻[13]討論得到。
1.3 振幅比A*、頻率比f*計算
引入渦強方程Γcos(2πfstt)=βUDq、無量綱位移y=Y/D、無量綱時間τ=tωst,化簡式(2)得到振子運動方程;引入范德波爾方程描述無量綱漩渦強度q,得到升力荷載變化方程。二式相互耦合,聯立得[14]:
(3)
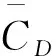
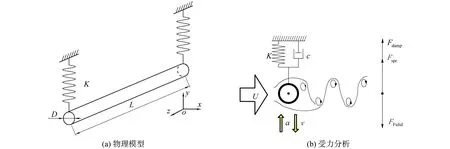
圖2 單自由度振子物理模型及受力分析Fig.2 Physical model and force analysis of single degree of freedom oscillator
振幅比A*是無量綱位移y的極值,振幅比f*是振子振動頻率與振子在水中的自振頻率的比值。使用四階龍格庫塔法求解式(3),時間步長取0.1,得到不同約化速度下振子隨周期振動的振幅比A*,對震蕩的時歷曲線進行傅里葉展開,求得頻率比f*。
1.4 功率計算
1.4.1 流體功率計算
水流做功的功率可以根據水流對振子的壓力乘以水流流速求得。根據伯努利方程,水流產生的動壓強為(ρU2)/2。常見的水流功率的計算方式有2種,即水流壓強作用面S取振子與流體直接接觸面的投影D×L,或取振子振動過程掃過的面積(2A+D)×L。這兩者并無本質區別,只是對流體動能利用的關注角度不同。本文采用后一種方案,且因連桿在水流方向的投影面積相比圓柱振子的投影面積可以忽略不計,忽略水流對連桿部分的作用力,取水流壓強的作用面為S=(2A+D)×L。水流功率表示為:
(4)
1.4.2 振子捕能功率計算
將式(2)流體附加阻尼項移到等式右側,得到:
(mosc+ma)y″+cstructurey′+Ky=
(5)
式(5)右側即水流力與流體摩擦的差值,左右相等,故左側部分積分即可得到振動系統捕獲的能量,而后再除以周期時長,即得到流體的平均有效功率。振子捕能包含振動系統的機械能、振動系統機械摩擦損耗2部分。其數值上與與水流對振子做的功相等。對能量及功率的計算為:
cstructurey′+Ky)y′dt
(6)
根據簡諧理論,振子運動位移y隨時間呈簡諧變化,即y=Asin(2πfosct),其中振子的振動主頻為fosc,其值為Tosc=1/fosc。在穩定振動中,液體與振子發生共振,根據結構動力學共振的規律,此時的振動主頻與升力主頻相等,即fosc=fFluid。
根據三角函數的奇偶性、周期性,含有y、y″的項積分后為0,代入式y、y′、y″,化簡為:
(7)
1.5 捕能效率計算
由于流量守恒,通過發電裝置的流體速度不會發生突變,電機轉換的能量僅由壓強差提供,因此流體能量損失天然地存在一個上限,即貝茨極限。在槳葉式發電裝置中貝茨極限取59.3%。此外,因為尾流粒子間、流體固體間的摩擦,振子不能充分利用水流本身的能量損失,因此振動系統對水流能量的利用率還要小于貝茨極限。定義振子捕能功率與流體損失功率的比值為捕能效率,表達式為:
(8)
式中:質量比m*、阻尼比ξ為結構參數;振幅比A*、頻率比f*為流固耦合參數;約化速度Ur為流體參數。流固耦合參數與流體、固體參數均相關,無法直接獲得,計算過程見2.3節。
2 捕能效率的影響分析
2.1 模型可靠性驗證及計算方案
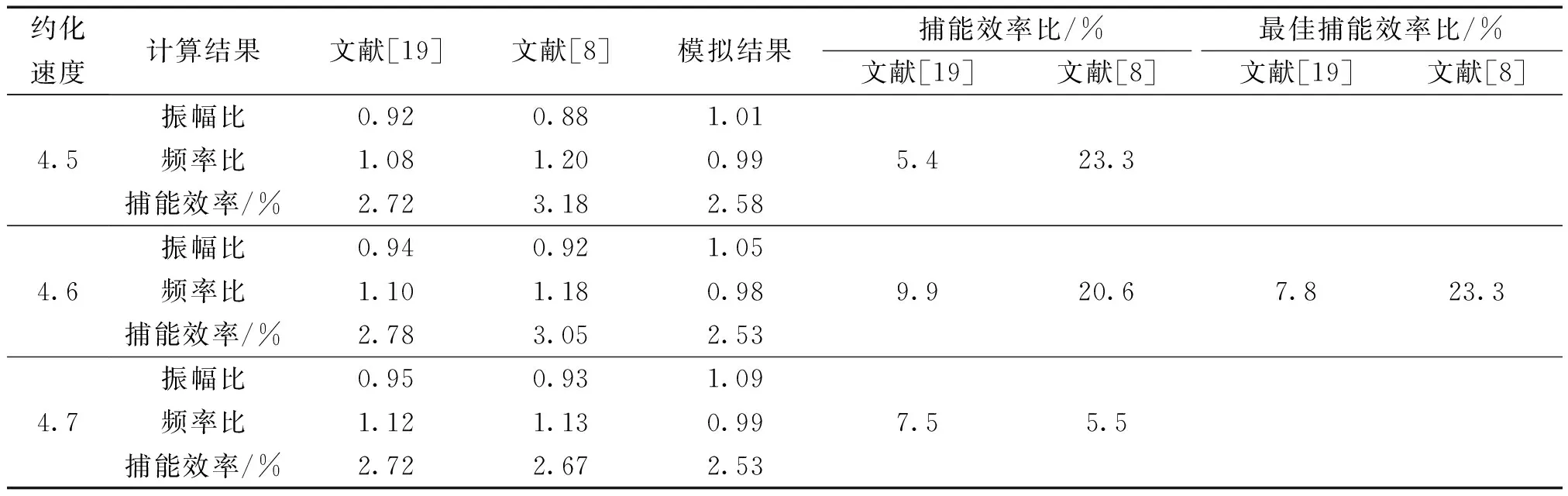
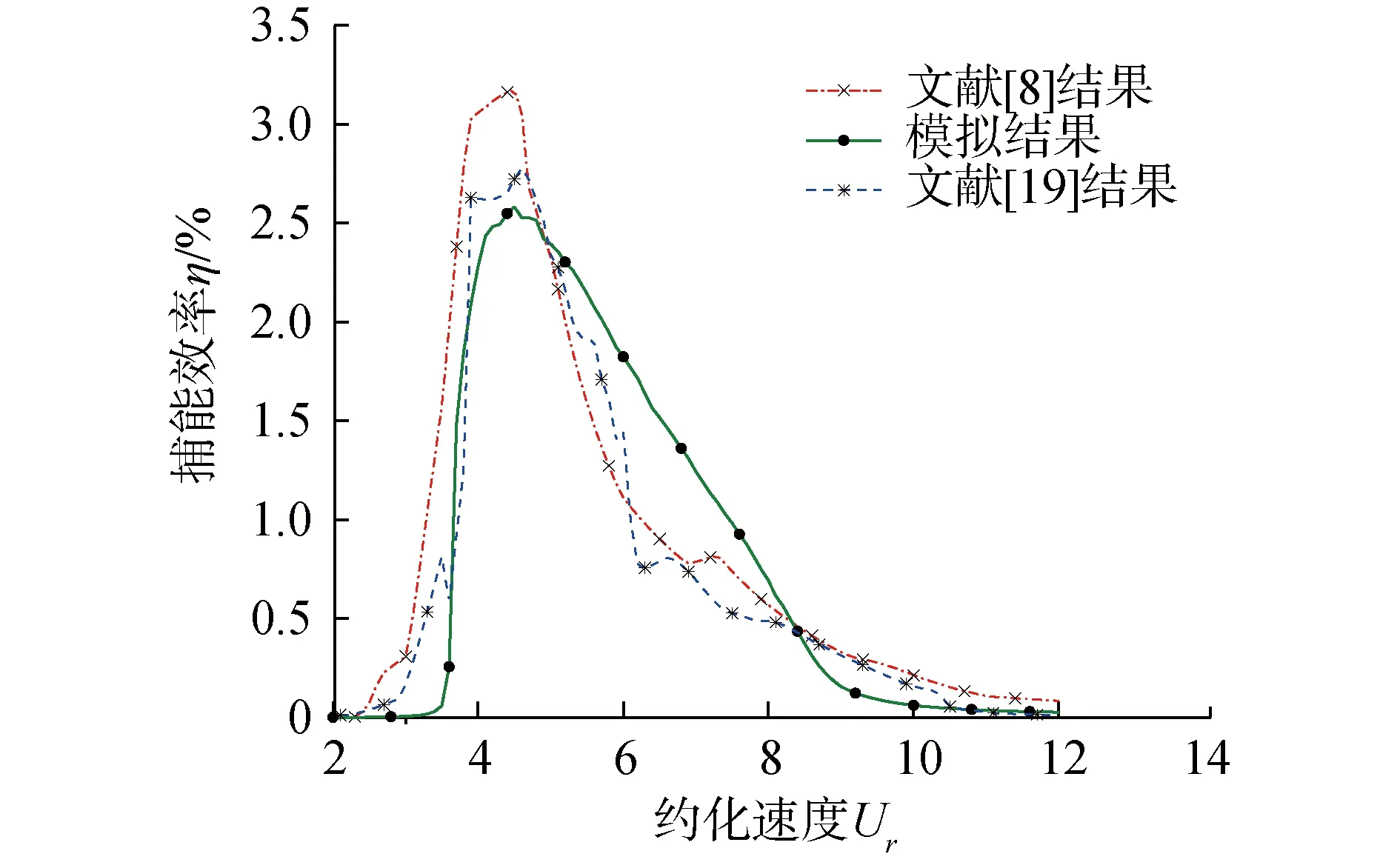
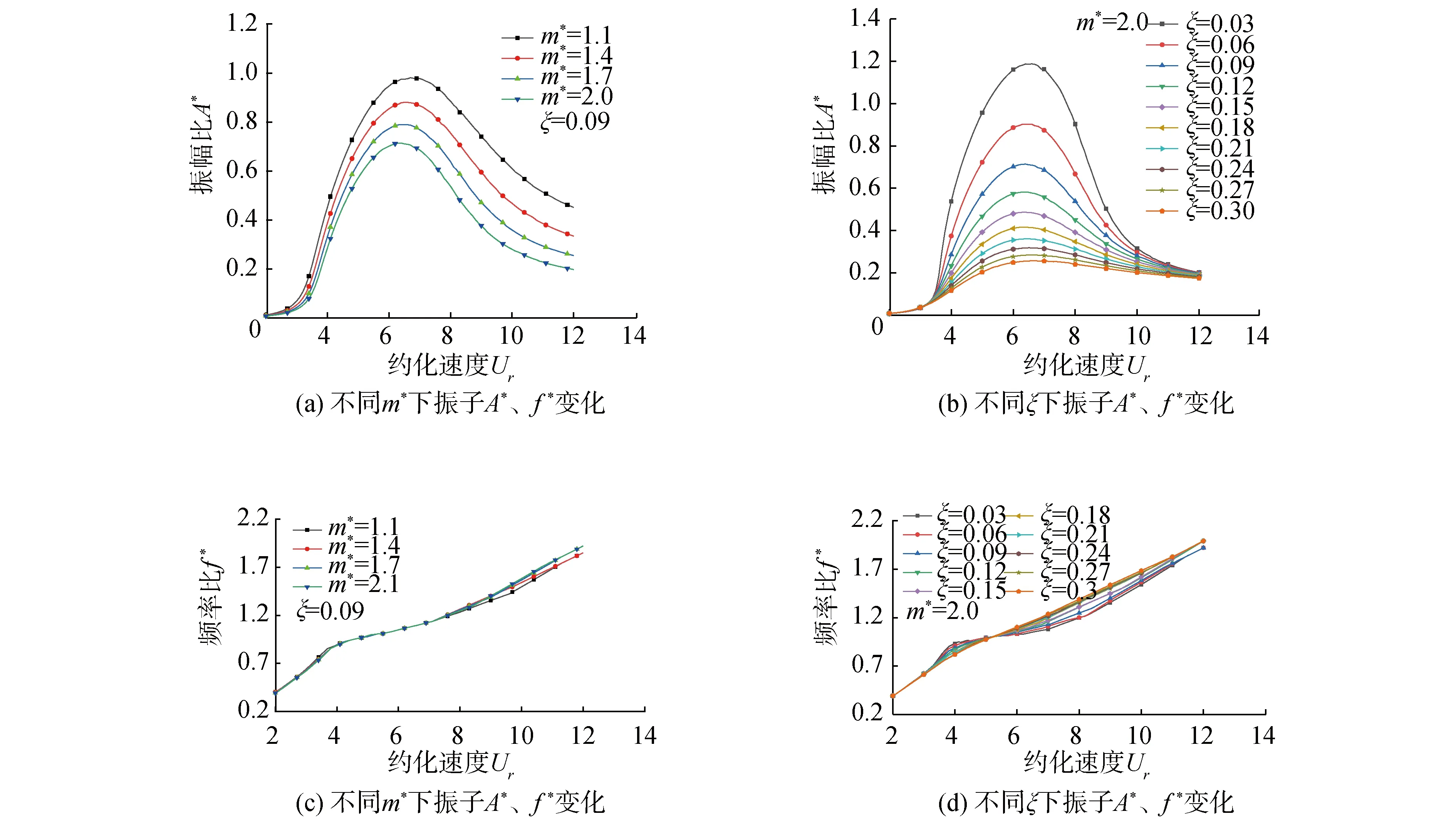
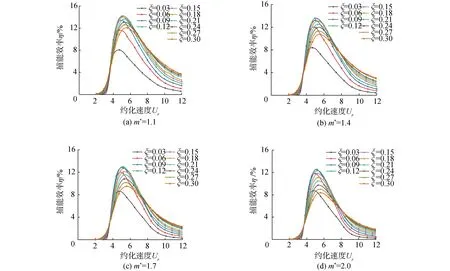
Khalak等[19]進行了m*=2.4、m*ξ=0.013的低質量比、低阻尼比物理實驗;羅竹梅[8]采用SSTk-ω高雷諾數湍流模型在相同的質量比、阻尼比下進行數值模擬。本文在相同條件下,使用尾流振子模型計算約化速度2 振子在不同約化速度下的3種捕能效率曲線如圖4所示。從圖中可以看出,本文模擬的曲線走勢與文獻結果較好吻合,最大捕能效率介于文獻[19]與文獻[8]的實驗、模擬結果,且極為接近。如表1所示,模擬的最大捕能效率與文獻結果的誤差分別是7.8%和23.3%,這說明了本文模擬方法的可靠性。模擬振動在Ur=4.5時獲得最大捕能效率2.58%,而參考文獻分別在Ur=4.5和Ur=4.6時對應取得最大捕能效率。相比下,模擬計算的整體捕能趨勢均略微滯后,這可能是范德波爾經驗參數取值偏小的緣故。 圖3 m*=1.4,ξ=0.03,Ur=4時振子時歷曲線及頻譜Fig.3 Curve of time and spectrum of oscillator vibration at m*=1.4,ξ=0.03,Ur=4 表1 計算結果可靠性驗證表Table 1 Reliability verification table of calculated results 圖4 各約化速度下振子捕能效率Fig.4 Energy capture efficiency of oscillator at different reduction velocities 根據模擬結果,振子共振穩定后的橫向振動響應近似正弦規律的諧波振動[8],取模擬計算的最后19個周期,以分析質量比、阻尼比對振子振幅比、頻率比、捕能效率的影響,并總結其相互關系。 隨約化速度的增加,不同質量比、阻尼比條件下的振子振幅比先增加后降低,質量比、阻尼比越低,振幅越大。記取最大振幅比的約化速度為最佳Ur,則振子的最佳Ur集中在6.3~6.9。最佳Ur值同阻尼比幾乎沒有關聯性,但會隨著質量比的增大稍稍提前。此外振幅比的變化率與質量比無關,但隨著阻尼比的減小,振幅比增大得越來越快。 頻率比同約化速度成正相關,其增大變化率經歷了陡峭-平緩-陡峭的過程。平緩階段4 由圖5(a)知,平緩區間內的頻率比與質量比無關。此外,不同阻尼比條件下頻率比隨約化速度的變化可以分成2個區間。區間一為3.3 圖5 不同m*、ξ下振子A*、 f*隨Ur變化變化圖Fig.5 Variation diagram of oscillator A*, f* with Ur under different m*, ξ 不同質量比、阻尼比下振子捕能效率隨約化速度的變化情況如圖6所示。 圖6 不同m*、 ξ下振子的捕能效率Fig.6 Energy capture efficiency of oscillator under different m*, ξ 1)總體而言,當約化速度處于4.5~6.4時,多數振子捕能效率η>10%,能量利用率較高。最大捕能效率見圖6(a),m*=1.1、ξ=0.15時,捕能效率η=14.27%,此時Ur=5.1。 2)在趨勢上,捕能效率η隨約化速度的增加先增加再降低,在約化速度Ur=5.3附近取得最大值,定義η取最大值對應的Ur為最優約化速度,此刻捕能效率稱為最優效率ηb。效率值η在遠離取最優Ur處變化平緩,在最優Ur鄰域也有較小變化率形成的緩和段,但在鄰域外側隨Ur變化的程度尤為激烈。同圖5的鎖定區間比較,最優鄰域恰好位于穩定共振區域,而位于進入、退出共振段區域的鄰域外側,捕能效率變化較大。 最優Ur的位置隨阻尼比的增大微微增大,與質量比的取值無關。 3)最優效率ηb隨質量比的變化見圖7,阻尼比ξ較小時,ηb與m*正相關;ξ較大時,ηb與m*反相關。這是由于隨著阻尼比的增大,振幅比迅速變小,同時頻率比在Ur=5.1附近幾乎沒有變化。 圖7 最優效率ηb隨質量比、阻尼比變化Fig.7 Optimal efficiency ηb varies with mass ratio and damping ratio 4)振子阻尼比較大時,最優效率ηb隨m*的變化越劇烈,從圖7可看出,對于不同的m*,均存在ξ使ηb取極大值。如式(8)所示,這是因為阻尼比較小時,阻尼比本身對效率的影響較大;隨著阻尼比增大,較大的阻尼比導致振幅比迅速減小,振幅比成為影響效率η的主導因子。不同質量比下取得最優效率的阻尼比數值可以由式(10)確定。 使捕能效率最大的阻尼比隨質量比的變化而改變,為獲取最優捕能效率,需要在模擬前估算最優阻尼比數值。用最小二乘法對ηb作關于m*、ξ的多項式曲面擬合,從而求解最優阻尼比,如圖8所示。 圖8 不同質量比、阻尼比變化下的最優效率ηbFig.8 Optimal efficiency ηbunder different mass ratio and damping ratio 曲面方程: ηb=0.707 6ξ2m*+13.54ξ3-0.419 2ξm*- (9) 擬合的復相關系數R-square=0.975 3,均方根誤差RMSE=0.003 007,誤差平方和SSE=0.000 298 4,故式(9)可以準確地描述質量比、阻尼比發生改變時,最優捕能效率ηb的變化趨勢。 對式(9)右側取關于ξ的偏導,并使其為零,得到關于m*、ξ的等式(10),即某一m*下取得最佳效率ηb的阻尼比ξ求解公式: (10) 分別代入m*=1.1到2,得ξ=0.148、0.138、0.128、0.117,符合對圖6的預測。這也間接驗證了式(9)的可靠性。 將m*=1.1、ξ=0.148代入式(9),得ηb=14.50%,即計算區域內的最大捕能效率。 1)振子的捕能效率峰值早于振幅比的峰值出現,這是由于振幅比、頻率比的增長速率較約化速度的增長速率變化較小的緣故。 2)根據模擬結果,振子在Ur=5.1、m*=1.1、ξ=0.15時,捕能效率取最大值ηb=14.27%;根據經驗公式,振子在m*=1.1、ξ=0.148時,捕能效率取最大值ηb=14.50%。 3)捕能效率隨約化速度的變化曲線存在最大值,最佳捕能效率對應的約化速度Ur位于區間[5.0,5.3]。 4)在式(9)所處的低質量比區間上,最優捕能效率與質量比成反相關,質量比越小捕能效率越高;但阻尼比存在使捕能效率達到最大的極值,其值隨著質量比的增大,由0.093降低至0.068。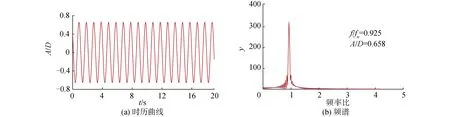
2.2 質量比、阻尼比對振子振幅比、頻率比的影響
2.3 不同質量比、阻尼比下捕能效率的分析
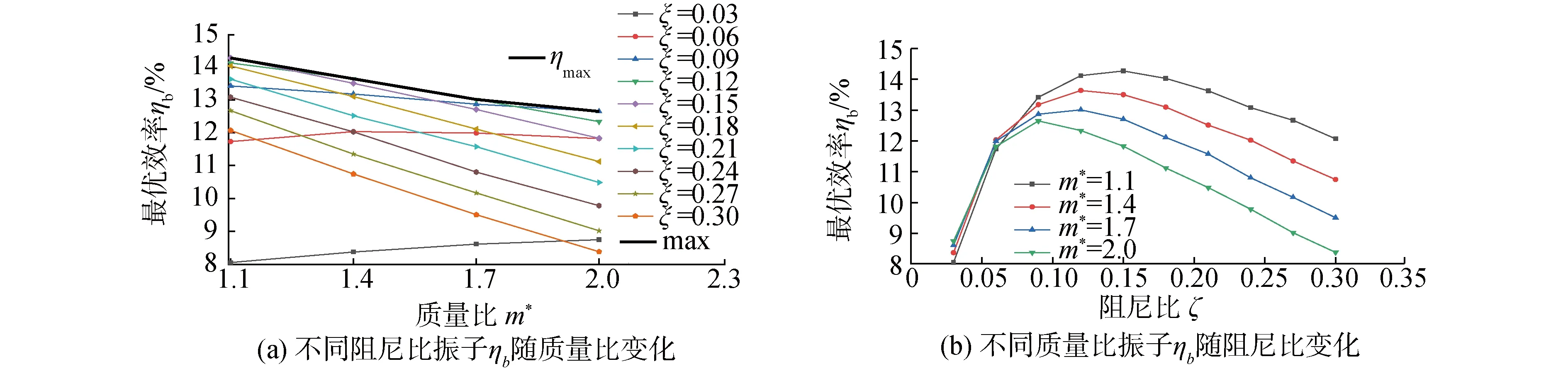
2.4 最優阻尼比分析
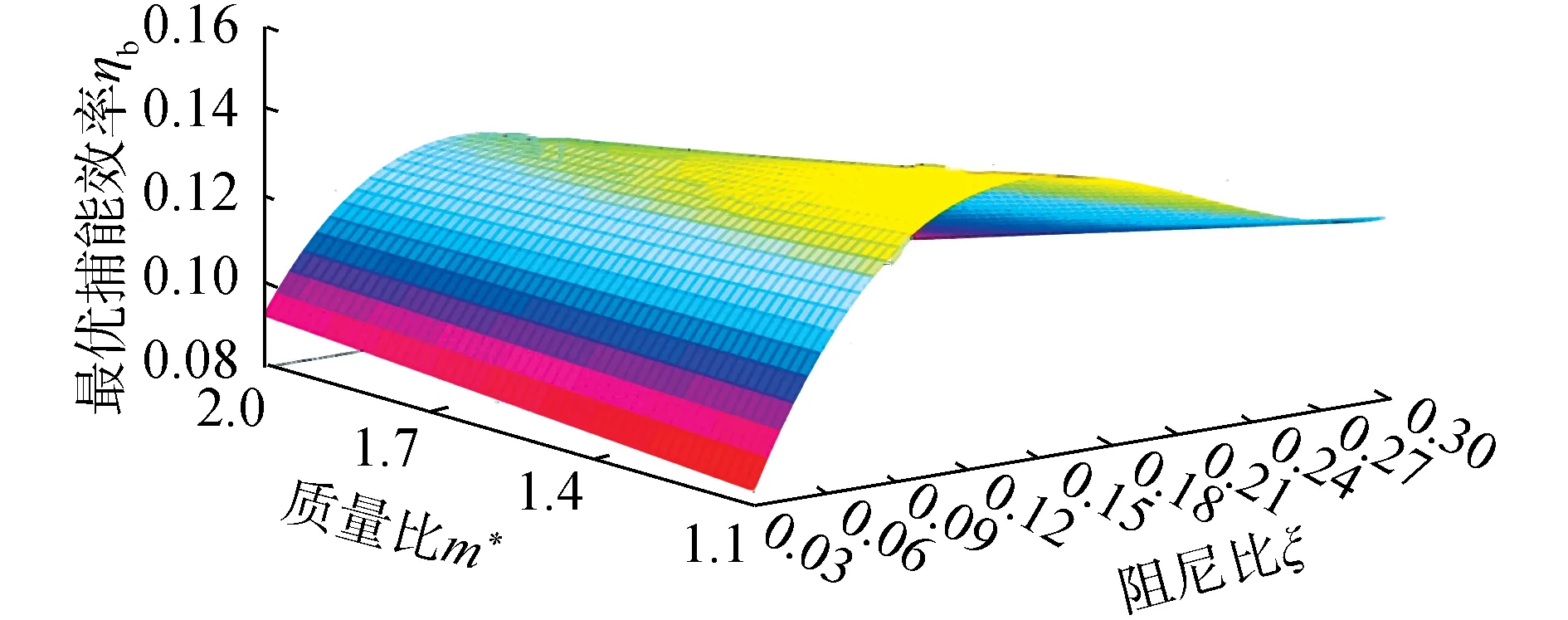
9.734ξ2+0.021 38m*+2.207ξ+0.015 35
(2≤Ur≤12;1.1≤m*≤2;0.03≤ξ≤0.3)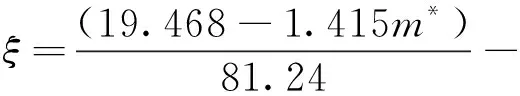
3 結論

