多并聯機構布局優化分析

王玉甲，王璐，唐寶富，徐文華

(1.哈爾濱工程大學 機電工程學院，黑龍江 哈爾濱 150001； 2.南京電子技術研究所，江蘇 南京 210039)

隨著陣面向大尺寸、輕薄化的方向發展，對其平面度的需求也不斷提高，傳統的支撐控制方式難以滿足其需求[1]。考慮到并聯機構具有位置誤差不會積累、剛度大、支撐面積大以及承載能力強的優點[2]，并且由于陣面尺寸相對較大，為盡量減小陣面的平面度，本文采用多組并聯機構支撐陣面，而多并聯機構的布局對陣面的變形有較大的影響，因此研究多并聯機構的布局優化方法具有重要的研究意義和實用價值。

目前國內外對于布局優化的研究主要集中在薄壁件的裝夾布局優化領域，而對于多并聯機構布局優化的研究則很少涉及，本文闡述薄壁件裝夾布局優化的研究現狀以供參考和借鑒。文獻[3]通過不斷改變薄壁件定位元件的位置，利用有限元方法得到其裝夾變形，最終得到最小裝夾變形對應的位置。文獻[4]以裝夾變形最小為目標函數建立最優化模型，并基于遺傳算法進行了最優布局的解算。文獻[5]建立了薄壁件裝夾變形的有限元模型，并以此分析定位元件位置等因素與裝夾變形量之間的關系。文獻[6]將有限元法和遺傳算法結合，以減小薄壁件的變形量為目標，對裝夾布局進行優化。文獻[7]以航空框類的銑削過程為研究對象，建立優化模型，利用遺傳算法對裝夾元件的數量和布局進行優化分析，并使用有限元軟件計算加工變形量，得到最優裝夾布局。

在以上的研究中，由于裝夾元件具有較小的結構尺寸，因此，可將其視為點支撐以開展分析計算，而在進行多并聯機構的布局優化時，由于其支撐面積較大，無法視為點支撐，并且并聯機構與陣面之間通過螺栓固定連接，陣面屬于剛柔耦合體，其變形情況非常復雜，很難通過傳統的布局優化方法進行求解；此外在這些研究中當采用最優化理論進行布局優化分析時，最優化模型的目標函數通常為工件的最大變形量，而工件的最大變形量只能反映其局部變形情況，因此求解得到的最優布局對應的陣面的整體變形情況不一定很好。

本文在采用基于有限元的布局優化方法進行最優布局的求解時發現該方法求解效率低下，當陣面尺寸較大時，并聯機構不同支撐布局的數目將會大大增加，求解時間將會很長。

因此，針對非點支撐結構、目標函數選擇及求解效率低下的問題，本文對支撐面積相對較大的多并聯機構布局優化問題開展研究，并以陣面平面度最小為優化目標，研究多元非線性回歸和遺傳算法相結合的布局優化方法，以提高計算效率。

1 基于有限元方法的布局優化

由于傳統的布局優化方法很難求解并聯機構支撐面積較大且陣面為剛柔耦合體的情況，而有限元方法非常適合用于這種變形情況復雜的場合，因此本文采用有限元方法解決多并聯機構的布局優化問題。

1.1 布局優化模型的建立

本文以2 000 mm×2 000 mm×5 mm(長×寬×高)的矩形陣面和支撐面長寬均為450 mm的4 組(通過“N-2-1”準則確定)并聯機構為例，將并聯機構與陣面邊線的距離設置為參數化變量，建立了陣面和多并聯機構的參數化模型，如圖1所示。

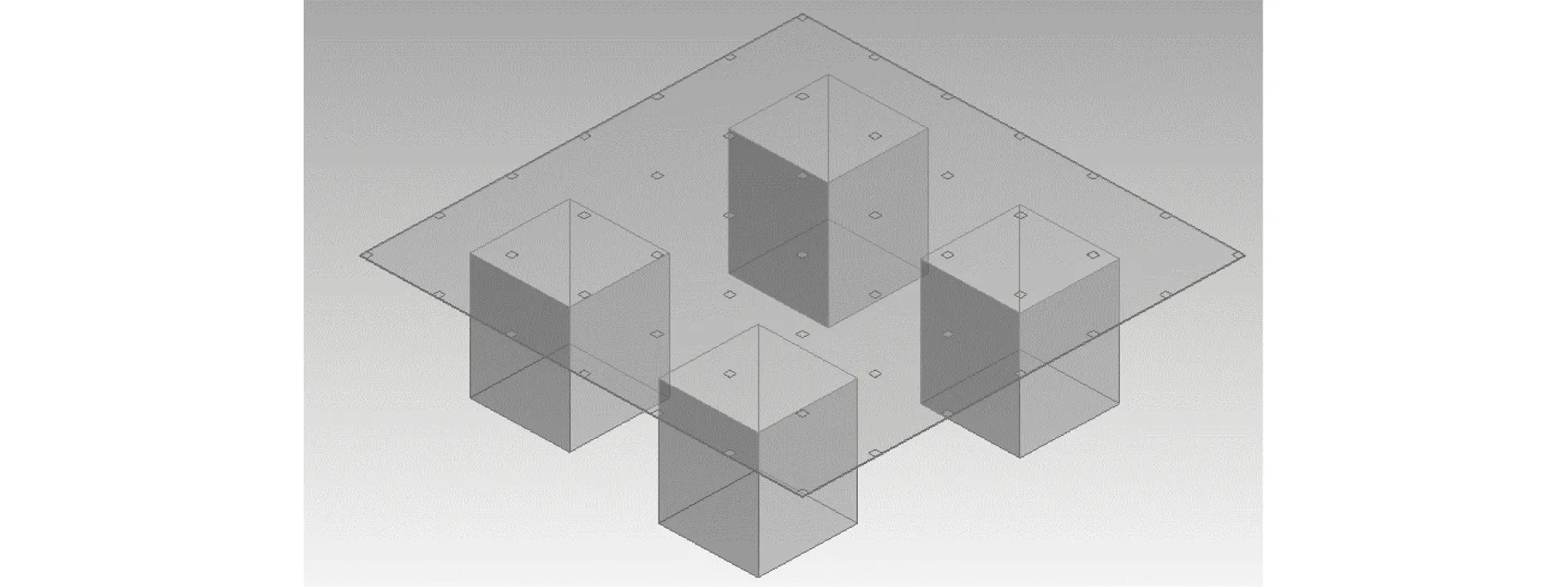
圖1 陣面和多并聯機構的參數化模型Fig.1 Parametric models of plane and multiple parallel mechanisms

基于最優化理論，優化模型的建立就是確定目標函數、設計變量及其約束條件。傳統的布局優化方法在建立最優化模型時其目標函數通常為工件的最大變形量，但最大變形量只能反映陣面的局部變形情況，不能很好地描述陣面的整體變形情況。而平面度是陣面具有的宏觀凹凸高度相對理想平面的偏差，可用來描述陣面整體的變形情況，因此，可以將被支撐平面的平面度最小作為多組并聯機構支撐布局優化的目標，以平面度為目標函數開展多組并聯機構的布局優化模型研究。

陣面的平面度誤差可以通過吻合精度，即陣面上多個采樣點撓度的均方根(root mean square，RMS)來表達，因此，以陣面的RMS值作為本文優化布局模型的目標函數[8]；約束條件為各并聯機構的支撐位置不重疊并且并聯機構的動平臺不能超出大型陣面的邊界；設計變量為并聯機構與大型陣面邊線的距離。

本文建立的支撐大型陣面的多并聯機構的布局優化模型為：

(1)

式中：F(X)為目標函數，即RMS；X為設計變量；Xd、Xu為X的下限值和上限值。

1.2 布局優化的分析計算

本文利用ANSYS Workbench進行多并聯機構布局優化分析，基于單目標自適應優化方法(adaptive single objective,ASO)，通過迭代求解，得到對應陣面平面度最小值的多組并聯機構的最優布局。

基于前述建立的參數化模型，首先進行用于平面度采樣點的選擇，考慮到陣面結構對稱性、尺度大小及其剛度影響，均勻選取陣面上的49個采樣點進行分析(如圖1所示)。針對本文設計的4 組并聯機構，可知共有8 個設計變量，考慮到支撐的對稱性及機構不能干涉，選擇并聯機構的支撐位置距陣面邊線的距離范圍為0～550 mm，布局優化過程的初始值為200 mm。

在進行布局優化計算時，考慮速度和成本等因素，本文設置樣本數為45 組((n+1)(n+2)/2，n為設計變量個數)，生成初始樣本后，分別計算其對應的RMS，并面向平面度最小，完成迭代計算。考慮仿真總時長，本文指定迭代8次，每次45個樣本，共計計算360 次，輸入變量縮減域的數目為8[9]。

通過布局優化迭代計算，得到陣面的平面度和并聯機構支撐位置的變化趨勢如圖2所示。可見，陣面的平面度漸進收斂至最小值，各并聯機構的支撐位置也逐漸收斂。

最優布局計算結果如圖3所示。

經過ANSYS Workbench計算給出了3組多并聯支撐機構的最優布局候選點，平面度均小于1 mm，滿足使用要求。

最優布局1的陣面RMS為2.058 8×10-5m(0.020 588 mm)，支撐位置為162.36 mm。通常，考慮到加工精度及安裝方便，一般要對計算值進行圓整處理，得到最優支撐位置。根據計算結果，本文將并聯機構中心點到陣面邊線的距離設定為390 mm，即圓整后選支撐位置為165 mm。此時，對應的陣面RMS仍為最小。

圖2 目標函數與設計變量變化趨勢Fig.2 Trend chart of target function and design variables

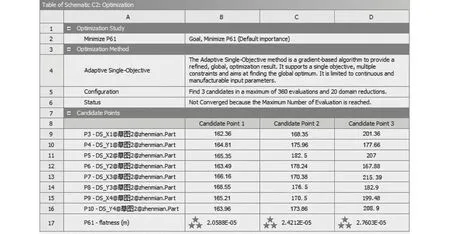
圖3 最優布局Fig.3 Optimal layout

1.3 最優布局與均勻布局結果對比

為了驗證本文優化布局方法的有效性，在ANSYS Workbench中求解均勻布局下陣面的平面度值，并進行對比分析，結果如表1所示。

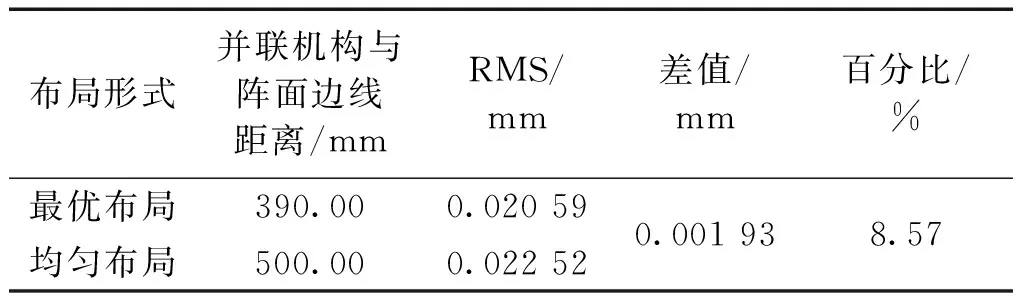
表1 最優布局與均勻布局結果對比

并聯機構的2種布局形式結果不同，但差異不大。最優布局情況下的RMS約為0.020 59 mm，而均勻布局情況下，即并聯機構中心點距離陣面邊線500 mm時，陣面的RMS約為0.022 52 mm，二者相差0.001 93 mm，最優布局相較于均勻布局，RMS值減小了8.57%，說明本文對并聯機構進行優化布局的有效性。但由于本文研究的陣面尺度較小，支撐機構數目較少且可變動的范圍也較小，優化布局方法對平面度RMS的改善并不顯著。

2 不同目標函數求解結果對比

為了驗證以陣面平面度最小為目標的最優布局方法的有效性，本文也對以陣面的最大變形量為目標函數的布局優化方法進行研究，并對比分析2種目標函數對優化結果的影響。

由于平面度表示的是陣面與理想平面之間的偏差，能夠很好地描述陣面整體的變形情況，因此仍以陣面的RMS為評價指標對2種目標函數表示方式進行評價。2種方式所求結果如表2所示。

表2 不同目標函數求解結果對比

由表2可知，當以陣面的平面度值為目標函數時，其最優布局為并聯機構中心點距離陣面邊線390 mm，對應的陣面的RMS值約為0.020 59 mm；當以陣面的最大變形量為目標函數時，其最優布局為并聯機構中心點距離陣面邊線530 mm，陣面的RMS值約為0.048 02 mm。2種目標函數表示方式的RMS差值為0.027 43 mm，以平面度為目標函數的方式相比于以最大變形量為目標函數的方式，其RMS值減小了57.12%，說明以平面度為目標函數求得的最優布局對應的陣面整體變形情況要更好，從而驗證了以平面度為目標函數的多并聯支撐機構布局優化方法的有效性。

3 基于多元非線性回歸和遺傳算法的布局優化

本文在研究基于ANSYS Workbench有限元分析的布局優化方法時發現其計算時間非常長。為了降低布局優化計算時間，提高計算效率，本文將多元非線性回歸理論和遺傳算法相結合，研究更加高效的多并聯機構布局優化方法。

3.1 多元非線性回歸模型的建立與驗證

本文首先基于有限元結果建立多并聯機構支撐位置和陣面的平面度的多元非線性回歸模型，再對模型的相關性和顯著性進行檢驗。

本文方法是根據有限元技術建立陣面平面度與并聯機構支撐位置的預測模型，便于求解不同支撐布局下陣面的平面度值，避免了漫長的有限元分析的過程，隨后采用遺傳算法求解最優解，提高求解最優布局的效率。

針對本文給出的陣面實例，考慮其對稱性，在計算中做一定程度的簡化，設定并聯機構按陣面的2條中心對稱布置，將求解4組并聯機構布局問題簡化為求解一個并聯機構支撐位置的問題。并聯機構的布局如圖4所示。

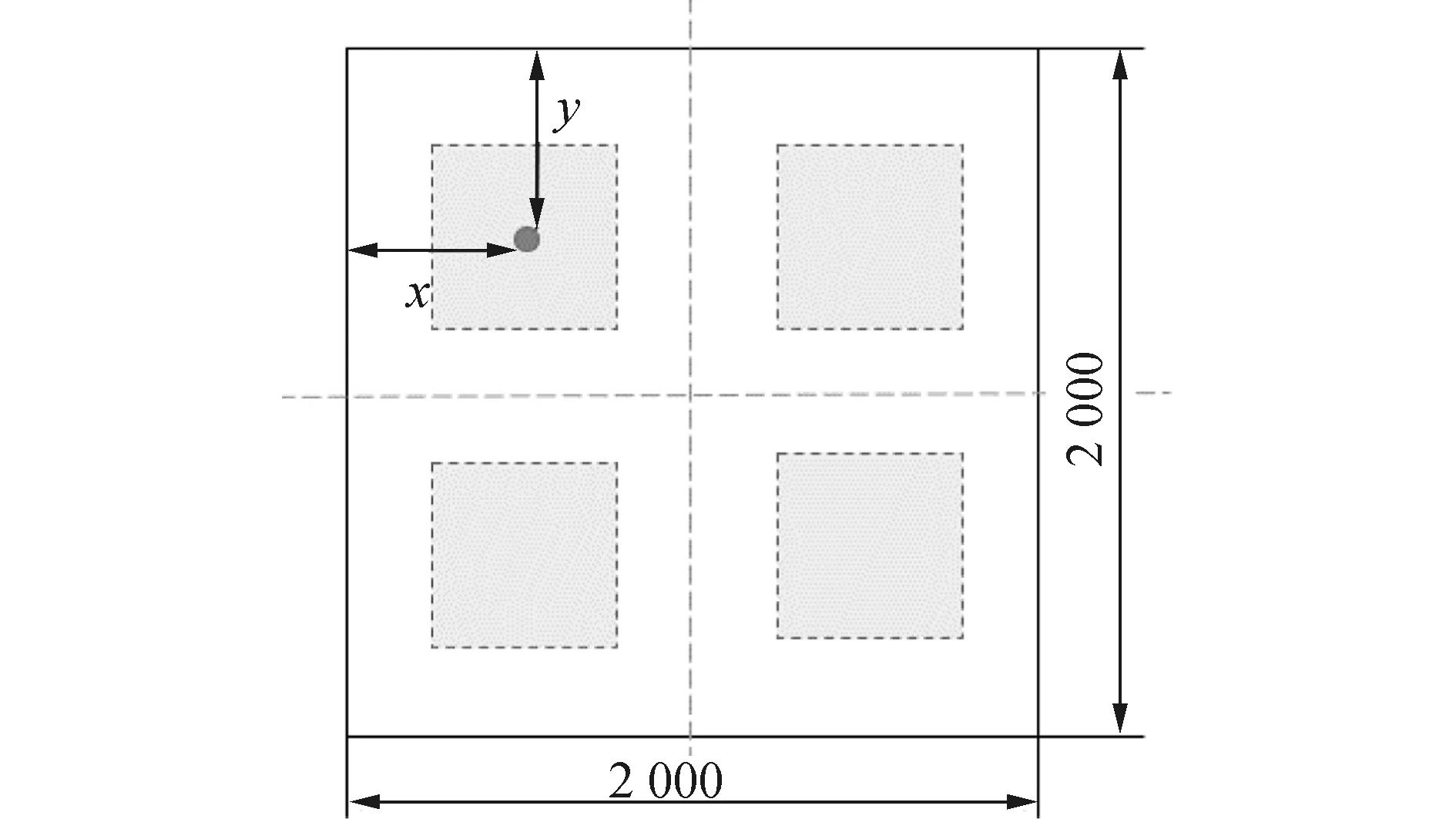
圖4 并聯機構布局示意Fig.4 Schematic diagram of parallel mechanism layout

本文以離散化的單個并聯機構的支撐位置(x，y)為自變量(范圍：225,230,…,775 mm)，以陣面的RMS為因變量，設計實驗方案。基于有限元方法計算得到不同布局下陣面的RMS值，得到36組多元非線性回歸樣本數據如表3所示。

表3 多元非線性樣本數據Table 3 Multivariate nonlinear sample data mm

使用1stOpt軟件對表3中的樣本數據進行擬合。通過基于麥夸特法(Levenberg-Marquardt)和通用全局優化法的迭代計算，在31代后達到收斂標準，得到待定多項式系數的近似解，以及并聯機構支撐位置x、y和陣面平面度f(x，y)之間的多元非線性回歸方程[10]：

f(x,y)=0.457 7-0.001 3x-0.001 1y+
1.537 1×10-6x2+4.782 8×10-7xy+
1.261 9×10-6y2

(2)

為了分析該方程的擬合效果，需要其進行相關性檢驗，計算得到其自變量和因變量之間的相關系數|R|=0.945 8，結果接近于1，說明方程的擬合效果很好。

在顯著性檢查中，設定顯著水平α為0.05，并由前述方案可得，在樣本數n為36，自由度數(即自變量個數)p為2時，Fβ(p,n-p-1)為3.32，回歸計算的F值為288.81。由于F≥Fβ，因此在給定的顯著性水平下，上述方程線性回歸顯著。

綜上，本文獲得的預測模型具有很好的擬合效果，可以用來表達并聯機構支撐位置和陣面平面度之間的關系。

3.2 耦合優化模型的建立

基于上述的多元非線性回歸方程，建立陣面平面度和多并聯機構支撐位置的耦合優化模型，并為應用遺傳算法進行布局優化分析提供前提。

耦合優化模型中，將并聯機構的支撐位置X=[x1,x2，…,xm]作為設計變量，將陣面的平面度預測值f(X)作為目標函數，將陣面上采樣點的撓度值ω作為狀態變量，ω既是X的函數，也是f(X)的重要參數；耦合優化模型的約束條件與前述分析相同。模型表達式(3)為：

(3)

3.3 布局優化計算

本文基于遺傳算法進行多并聯機構的布局優化分析，求解得到最優布局。各代種群中最優解的分布位置的散點圖如圖5所示。

圖5 各代種群最優解分布位置Fig.5 Distribution location map of optimal solutions for generation population

由圖5可見，在(380 mm，380 mm)附近，并聯機構支撐位置最優解分布較為集中，少數最優解分布較分散，其原因是在初始迭代過程中，最優解及其支撐位置還未收斂，離散性較大，隨著迭代次數增加，最優解對應的支撐位置逐漸收斂于380 mm附近區域。

在每一代種群中，各個體對應的支撐位置也各不相同，最后一代種群所有個體的分布位置散點圖如圖6所示。可見，同一代種群中，大多數個體對應的支撐位置的分布也主要集中在某一區域，同時也存在一些個體對應的支撐位置分布在較離散的區域，這也反映了種群中個體多樣性，有利于代間遺傳。

圖6 最后一代種群個體分布Fig.6 Individual distribution map of the last generation population

遺傳過程中，各代種群的目標函數的最小值如圖7所示。從圖中可見，在遺傳20代左右，目標函數即平面度收斂到最小值0.009 678 mm，獲得最優解。

圖7 目標函數最小值隨遺傳代數變化曲線Fig.7 Change diagram of population objective function and genetic algebra

遺傳過程中，每一代種群的個體目標函數平均值如圖8所示。從圖中可見，在遺傳20代左右以后，目標函數平均值在0.013 mm上下波動，說明多數個體在種群內的分布集中性較好，同時，波動范圍趨于平穩，也說明了種群內個體任然具有一定的多樣性。

圖8 種群中個體目標函數平均值曲線Fig.8 Diagram of average value of individual objective function in population

綜上，基于遺傳算法結果，經過最優解的圓整，可得并聯機構的最優支撐位置為(380 mm，380 mm)，陣面的平面度值約為0.009 678 mm。

3.4 2種布局優化方法的對比分析及應用

針對多并聯機構的布局優化問題，本文分別研究了采用有限元軟件的布局優化方法和基于多元非線性回歸和遺傳算法相結合的布局優化方法，并針對給定尺寸的陣面完成了布局優化分析，現對以上2種方法進行對比，結果如表4所示。

表4 2種布局優化方法的對比

由表4可知，基于有限元的布局優化方法求解時間長達10 h，其最優布局為并聯機構距離陣面邊線390 mm；而基于多元非線性回歸和遺傳算法的布局優化方法求解時間僅為1 min，其最優布局為并聯機構距離陣面邊線380 mm。

基于前述計算結果可知，布局結果在最優解附近相差10 mm，陣面平面度相差極小，可以滿足給定的技術要求，同時，在支撐范圍變化量為550 mm的前提下，該差值相對于變化范圍的百分比約為1.8%，可以認為2種求解方法結果接近。進一步驗證了本文所研究的基于多元非線性回歸和遺傳算法的方法的快速性和準確性。

基于以上分析，本文給出如下建議：

1)對于陣面尺度較大、形狀規則(如對稱結構)、支撐機構數量確定的情況，可采用基于多元非線性回歸和遺傳算法的布局優化方法。

2)對于陣面尺度較小、形狀不規則、并聯機構數量不確定的情況，可采用基于有限元軟件的布局優化方法。

4 結論

1)本文在ANSYS Workbench中使用基于迭代的單目標優化方法，通過改變各并聯機構的支撐位置進行優化分析，求得的最優布局為并聯機構距離陣面邊線390 mm，對應的陣面最小平面度值約為0.020 59 mm，滿足了技術指標中1 mm的平面度要求。與均勻布局相比，陣面的平面度值減小了8.57%。

2)本文以陣面最大變形量為目標函數進行了布局優化分析，求得的最優布局為并聯機構距離陣面邊線530 mm，其對應的陣面平面度值約為0.048 02 mm，2種目標函數表示方式的最優布局對應的陣面平面度值相差0.027 43 mm，以陣面平面度值為目標函數的方式與該方式相比，其RMS值減小了57.12%。

3)針對有限元方法求解時間過長的情況，本文研究了基于多元非線性回歸和遺傳算法的布局優化求解方法，求得的并聯機構的最優支撐位置距離陣面邊線380 mm，與有限元方法的得到的距離相差10 mm，其相對于距離變化范圍的百分比約為1.8%，且2種方法所求平面度結果非常接近。而該方法求解時長約1 min，遠小于有限元方法的10 h，驗證了該方法的有效性。