從導數基本定義切入解題 正確開啟高考復習模式
安徽 石新星 王成功
導數是高考的必考考點,主要考查方向是導數的概念、導數的幾何意義、導數與函數的單調性、導數與函數的極值和最值、導數與不等式以及導數與方程等.足見導數在高考中比重大、考查角度廣、難度大、對學生綜合素質要求高.很多學生會因為找不到有效的解題方法而放棄導數題.其實解決導數問題的方法是多種多樣的,這給原本就有很大難度的導數問題披上了更加神秘的面紗.然而,萬變不離其宗,高考立足于課本基礎知識、基本定義,考查的是學生的綜合能力.本文筆者將從巧用導數的定義出發,給出破解導數問題的一般方法,以饗讀者.意在讓我們的高三師生,在高考復習的時候能夠正確開啟復習之門,立足課本,把握知識的本質,掌握以不變應萬變的解題策略.
一、試題呈現
【例1】(2018·全國卷Ⅰ文·21)已知函數f(x)=aex-lnx-1.
(Ⅰ)設x=2是f(x)的極值點,求a,并求f(x)的單調區間;
【例2】(2019·全國卷Ⅰ文·20)已知函數f(x)=2sinx-xcosx-x,f′(x)為f(x)的導數.
(Ⅰ)證明:f′(x)在區間(0,π)存在唯一零點;
(Ⅱ)若x∈[0,π]時,f(x)≥ax,求a的取值范圍.
二、問題探究
【例1分析】(Ⅰ)求出導函數f′(x),由f′(2)=0,求出a,并驗證x=2是f(x)的極值點,進而求出f(x)的單調區間;(具體解析略)
以上兩個思路都是解決導數與不等式問題的常規思路,思路一,無需過多的對函數進行變形,但是需要對導函數的一部分繼續求導,計算量大,處理起來較為麻煩.思路二,利用單調性和放縮思想,重新構造函數,結合不等式的傳遞性來求解,這種思路把函數具體化了,避免了繁雜的計算.橫觀這兩個解題思路,總有一種為了解題而解題的感覺,這樣做也未能體現出高考題立足課本知識,是對課本知識的延續和拓展的特點.翻開課本(人教A版高中數學選修2-2第19頁),課后習題B組第2題:
設函數f(x)=1-ex的圖象與x軸相交于點P,求曲線在點P處的切線的方程.
那么本題第二問會不會也與切線有關系呢?能否從切線的角度來尋找破題方法呢?
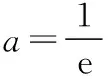
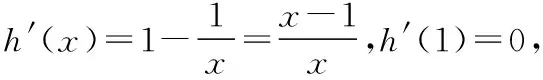
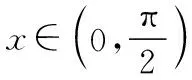
【解析】(Ⅰ)f′(x)=2cosx-cosx+xsinx-1=cosx+xsinx-1,
令g(x)=cosx+xsinx-1,則g′(x)=-sinx+sinx+xcosx=xcosx,
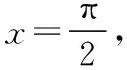
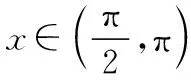
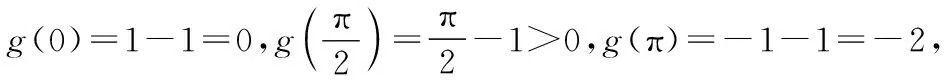
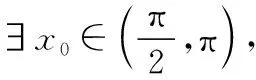

綜上所述,f′(x)在區間(0,π)存在唯一零點.
(Ⅱ)若x∈[0,π]時,f(x)≥ax,即f(x)-ax≥0恒成立,
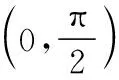
①當a≤-2時,h′(x)min=h′(π)=-2-a≥0,即h′(x)≥0在[0,π]上恒成立,所以h(x)在[0,π]上單調遞增,所以h(x)≥h(0)=0,即f(x)-ax≥0,此時f(x)≥ax恒成立;
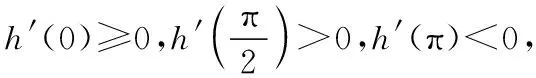
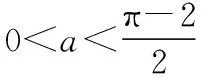
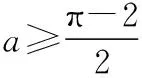
【嘗試切線法思路】因為y=ax過原點,且h(x)=2sinx-xcosx-x的圖象也過(0,0)點,設曲線h(x)在(0,0)處的切線斜率為k,因此a≤k成立即可.
【解析】令h(x)=2sinx-xcosx-x,所以h′(x)=2cosx-cosx+xsinx-1,所以h′(0)=2cos0-cos0+0-1=0,所以若x∈[0,π]時,f(x)≥ax,則a∈(-∞,0].
通過以上兩道高考試題的解題過程比較,我們不難發現,從導數的定義入手,巧用切線思想,不僅能夠快速找到解題方法,而且會讓很多復雜的問題變得更加簡單.這也就要求教師在高三復習的時候,不能帶著學生沉浮于題海中,而是要站在課本定義和概念的瞭望塔上,找到解題的方向.
三、拓展推廣——切線是破解導數題的利刃
用切線來解決導數問題,不是以上兩例的專屬方法.也不是我們所想的“巧合”,而是各類試題命制的角度,更是“新課程標準”和高考“考試說明”對課本基礎知識的要求.也是高考對學生基本能力的考查.所以,用導數的切線來尋找解決問題的方法是可以在一定范圍內推而廣之的,并且是行之有效的.
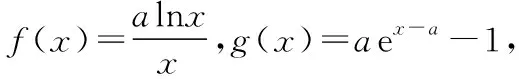
(1)求實數a的值以及切點坐標;
(2)求證:g(x)≥f(x).
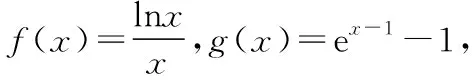
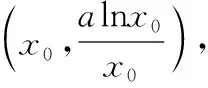
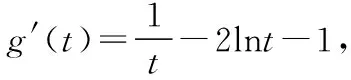
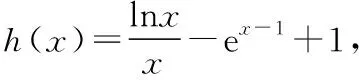
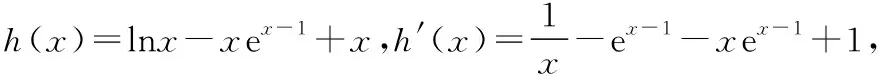
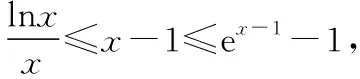

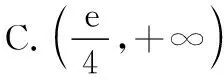
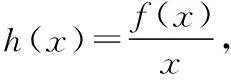
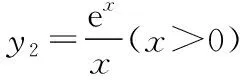
解法三:作為選擇題,本題可以通過比較選項,利用排除法只需要驗證a=1和a=4時是否滿足題意即可.
利用切線解決導數問題,不是只適用于特殊問題,而是具有一般性的,可以解決的是一類問題,只是有的題目利用切線來解決可能構造的函數較復雜或者是計算繁雜.


