學(xué)會歸類與整理,突破函數(shù)不等式

甘肅 張建文

函數(shù)類不等式的證明是導(dǎo)數(shù)壓軸題中非常重要的一類不等式,這類不等式在高考題和模擬題中是經(jīng)常見到的.不同于其他類型的不等式,函數(shù)類不等式的證明基本上是通過對不等式進(jìn)行等價變形、構(gòu)造相應(yīng)的函數(shù)、求解函數(shù)最值來實現(xiàn)的.不等式的變形與函數(shù)構(gòu)造因不等式結(jié)構(gòu)的不同而有所區(qū)別.本文通過研究函數(shù)類不等式的組成元素和處理方法，歸納整理知識之間的邏輯關(guān)系,得到證明函數(shù)類不等式的通性通法.下面筆者就不同類型的函數(shù)類不等式的變形方法和函數(shù)構(gòu)造原則進(jìn)行簡單論述.

一、常見函數(shù)類不等式證明方法

1.直接法求解函數(shù)最值

當(dāng)x∈I時,證明:不等式f(x)≥g(x)成立.

思路1:f(x)≥g(x)?f(x)-g(x)≥0,令h(x)=f(x)-g(x),只需求出x∈I時,hmin或h(x)的下確界即可.

思路2:f(x)≥g(x)?g(x)-f(x)≤0,令h(x)=g(x)-f(x),只需求出x∈I時,hmax或h(x)的上確界即可.

2.尋找充分條件,確定中間參考值

當(dāng)x∈I時,證明:不等式f(x)≥g(x)成立.

不等式f(x)≥g(x)成立的一個充分不必要條件是f(x)min≥g(x)max,進(jìn)而構(gòu)造函數(shù)y=f(x)和y=g(x).求解y=f(x)的最小值或下界,y=g(x)的最大值或上界.這種證明方法只適用于某一類特殊不等式,一般需要我們計算出兩函數(shù)對應(yīng)的最值.

3.放縮法

放縮法是證明不等式的一種重要的手段，因其思維量大，構(gòu)造性強，需要有較高的放縮技巧，能夠全面綜合地考查學(xué)生的學(xué)習(xí)能力，因而經(jīng)常成為高考壓軸題的命題素材.這類問題的解決通常是通過多角度觀察式子結(jié)構(gòu),深入剖析其中的特征,抓住其規(guī)律進(jìn)行恰當(dāng)?shù)胤趴s,從而使問題得以解決.

4.分析綜合法

分析法的思路是逆向思維,用分析法證明必須從結(jié)論出發(fā),倒著分析,尋找命題成立的充分條件.應(yīng)用分析法證明問題時要嚴(yán)格按照分析法的語言表述,下一步是上一步的充分條件.用綜合法證明時,必須首先找到正確的出發(fā)點,多角度聯(lián)想已知條件,層層推進(jìn),從而由已知推出結(jié)論.分析綜合法是分析法和綜合法的結(jié)合,證明思路一般是運用分析法對結(jié)論進(jìn)行推導(dǎo),找到成立的充分條件,再利用綜合法從已知條件出發(fā)推出此條件成立,從而命題得以證明.

二、特殊不等式化簡原則

1.只含有l(wèi)nx的不等式化簡原則

若不等式f(x)≥g(x)中只含有xlnx和x的整式表達(dá)式,此時我們首先考慮直接法構(gòu)造函數(shù)求解,若無法求解則轉(zhuǎn)而要考慮f(x)≥g(x)的結(jié)構(gòu)特點,比如有xlnx時考慮將lnx與x分離進(jìn)行思考,這樣可以在導(dǎo)函數(shù)中避免出現(xiàn)lnx,簡化運算過程.

2.只含有ex的不等式化簡原則

不等式f(x)≥g(x)中只含有ex和x的整式表達(dá)式.對于這類不等式,通常對不等式進(jìn)行等價變形,構(gòu)造恰當(dāng)?shù)暮瘮?shù)來求解最值.等價變形是按照簡化運算的原則進(jìn)行:

①嘗試構(gòu)造函數(shù)h(x)=f(x)-g(x),求解h(x)的最小值或下界;

②若①無法實現(xiàn),則考慮將ex與其他表達(dá)式整合,變形為exh(x)≥1或exh(x)≤1,構(gòu)造函數(shù)y=exh(x),求解相應(yīng)的最值或邊界值.

3.同時含有ex和lnx的不等式化簡原則

若不等式f(x)≥g(x)中含有l(wèi)nx與ex,通常需要將lnx與ex分離在不等號的兩側(cè),再觀察不等式的特點,必要的時候需要在不等式的兩邊同除以或乘以x進(jìn)行變形,最后構(gòu)造函數(shù)求解最值證明.

三、典例賞析

1.直接法證明函數(shù)類不等式

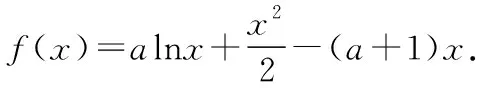
(1)當(dāng)a>0時,求函數(shù)f(x)的單調(diào)區(qū)間;

解析:(1)當(dāng)01時，f(x)在(0，1)，(a,+∞)上單調(diào)遞增，在(1，a)上單調(diào)遞減.

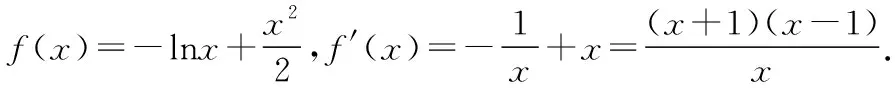
所以當(dāng)x∈(0,1)時,f′(x)<0,f(x)單調(diào)遞減;當(dāng)x∈(1,+∞)時,f′(x)>0,f(x)單調(diào)遞增.

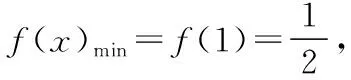
點評:直接法是易于理解、便于操作的證明方法,對于難度不大的證明題通常選用這種方法證明.此題只需判斷清楚函數(shù)單調(diào)性就能求出最值,證明結(jié)論.在解答完成后需要教師引導(dǎo)學(xué)生進(jìn)行歸類總結(jié),獲得通性通法.

2.尋找充分條件,確定中間參考值

【例2】已知函數(shù)f(x)=1-lnx+a2x2-ax(a∈R).

(1)討論函數(shù)f(x)的單調(diào)性；

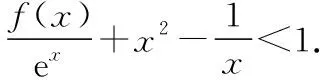
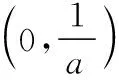
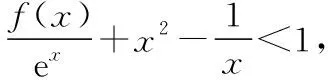
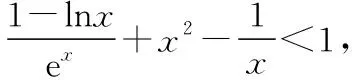
當(dāng)x∈(0,1)時,令g(x)=x(1-lnx),下面求解g(x)的最大值或上界.

由g′(x)=-lnx>0,g(x)在(0,1)上單調(diào)遞增,所以g(x)

令h(x)=(1+x-x3)ex,下面求解h(x)的最小值或下界.

h′(x)=(2+x-3x2-x3)ex,令p(x)=2+x-3x2-x3,則p′(x)=1-6x-3x2.

由于y=p′(x)在(0,1)上單調(diào)遞減,p′(0)=1,且p′(1)=-8,所以p′(x)有一個零點,記為x0.

當(dāng)x∈(0,x0)時,p′(x)>0,p(x)單調(diào)遞增；當(dāng)x∈(x0,1)時,p′(x)<0,p(x)單調(diào)遞減.

當(dāng)x∈(0,x0)時,p(x0)>p(0)=2,當(dāng)x∈(x0,1)時,p(x0)p(1)<0.所以p(x)在x∈(x0,1)存在唯一零點,記為x1.

當(dāng)x∈(0,x1)時,p(x)>0,h′(x)>0,h(x)單調(diào)遞增;當(dāng)x∈(x1,1)時,p(x)<0,h′(x)<0,h(x)單調(diào)遞減.所以h(x)>min{h(0),h(1)}=min{1,e}=1.

故而(1+x-x3)ex>1,x(1-lnx)<1,即x(1-lnx)<(1+x-x3)ex,原式成立.

點評:此題的證明思路在于將lnx與ex分離在不等號的兩側(cè),運用分析法尋找不等式成立的充分條件，構(gòu)造兩個函數(shù)分別求取最值.此題對學(xué)生的觀察能力要求極高,不僅需要敏銳地觀察出式子的結(jié)構(gòu)特點,對不等式進(jìn)行恰當(dāng)變形,而且還需要構(gòu)造雙函數(shù)解答.

3.放縮法證明不等式

(1)求曲線y=f(x)在點(0,-1)處的切線方程;

(2)證明:當(dāng)a≥1時,f(x)+e≥0.

解析:(1)2x-y-1=0.

令g(x)=x2+x-1+ex+1,g′(x)=2x+1+ex+1,顯然g′(x)在R上單調(diào)遞增,且g′(-1)=0.

當(dāng)x∈(-∞,-1)時,g′(x)<0,g(x)單調(diào)遞減;當(dāng)x∈(-1,+∞)時,g′(x)>0,g(x)單調(diào)遞增.

所以當(dāng)x=-1時,gmin=g(-1)=0,即g(x)≥0,所以f(x)+e≥0，原式得證.

點評:此題利用放縮法對不等式進(jìn)行放縮,將不等式中的a處理掉,轉(zhuǎn)化為不含參數(shù)的不等式,再通過構(gòu)造函數(shù)求解最值進(jìn)行解答.能否應(yīng)用放縮法關(guān)鍵要看不等式的結(jié)構(gòu)是否滿足放縮條件,教師要引導(dǎo)學(xué)生多角度多層次觀察,從最常規(guī)的解法開始思考,嘗試各種可能性,尋求滿足本題目的最優(yōu)解法.

4.分析綜合法

【例4】已知函數(shù)f(x)=xlnx,g(x)=-x2+mx-2.

(1)若函數(shù)y=f(x)-g(x)有且僅有一個零點,求實數(shù)m的值;

(2)已知函數(shù)h(x)=f(x)-kx2-x,a,b為h(x)的兩個極值點(ae2.

解析:(1)m=3.

(2)h(x)=xlnx-kx2-x,x∈(0,+∞),h′(x)=lnx-2kx.由于a,b為h(x)的兩個極值點,

所以有F(a)=F(b),0

點評:此題屬于極值點偏移問題,需要對結(jié)論按照分析法尋找成立的充分條件.此題不僅僅對結(jié)論進(jìn)行等價變形,而且還利用函數(shù)單調(diào)性進(jìn)行化簡.在構(gòu)造G(x)后求導(dǎo)過程需要用復(fù)合函數(shù)的求導(dǎo)法則,先求導(dǎo)后代入,這樣可以極大地簡化運算過程.

5.只含有l(wèi)nx的不等式

【例5】已知f(x)=x(lnx+ax+1)-ax+1.

(1)若f(x)在[1,+∞)上是減函數(shù),求實數(shù)a的取值范圍;

(2)若實數(shù)a=-2,證明:f(x)的最大值為2.

解析:(1)a≤-2.

(2)當(dāng)a=-2時,f(x)=x(lnx-2x+1)+2x+1,欲證f(x)的最大值為2,

當(dāng)x∈(0,1)時,g′(x)>0,g(x)單調(diào)遞增;當(dāng)x∈(1,+∞)時,g′(x)<0,g(x)單調(diào)遞減.

所以當(dāng)x=1時,g(x)max=g(1)=0,即g(x)≤0,原式成立.

點評:此題的證明關(guān)鍵在于對不等式xlnx-2x2+3x-1≤0的處理,不等式含有xlnx,需要出現(xiàn)單獨的lnx,這樣能極大地簡化運算過程.若是直接構(gòu)造函數(shù)y=xlnx-2x2+3x-1,最大值的求解是相當(dāng)煩瑣的,對于絕大多數(shù)學(xué)生來說是求不出來的.因此教師要引導(dǎo)學(xué)生觀察式子結(jié)構(gòu),構(gòu)造恰當(dāng)?shù)暮瘮?shù)進(jìn)行運算.

6.只含有ex的不等式

【例6】(2018·全國卷Ⅱ理·21)已知函數(shù)f(x)=ex-ax2.

(1)若a=1,證明:當(dāng)x≥0時,f(x)≥1;

(2)若f(x)在(0,+∞)只有一個零點,求a.

當(dāng)x=0時,g(x)max=g(0)=1,即g(x)≤1.原式得證.

【例7】已知函數(shù)f(x)=ex-x2+x-1，x∈[0,+∞).證明:f(x)≥0.

當(dāng)x∈[0,1)和(2,+∞)時,g′(x)<0,g(x)單調(diào)遞減;當(dāng)x∈(1,2)時,g′(x)>0,g(x)單調(diào)遞增.

所以g(x)max=max{g(0),g(2)}=g(0)=1,即g(x)≤1.原式得證.

點評:例6和例7中的不等式都含有ex和x的整式表達(dá)式,按照思路2進(jìn)行變形.數(shù)學(xué)解答的思路通常“看”出來的,教師要引導(dǎo)學(xué)生學(xué)會觀察,教會學(xué)生“看”的方法.例7中的函數(shù)最大值求解需要借助于函數(shù)的簡單圖象,在訓(xùn)練推理論證能力的同時可以培養(yǎng)學(xué)生的直觀想象素養(yǎng).

7.同時含有ex和lnx的不等式

(1)討論函數(shù)f(x)的單調(diào)性;

當(dāng)x∈(0,1)時,h′(x)<0,h(x)單調(diào)遞減;當(dāng)x∈(1,+∞)時,h′(x)>0,h(x)單調(diào)遞增.

所以當(dāng)x=1時,h(x)min=h(1)=e,即h(x)≥e,當(dāng)且僅當(dāng)x=1時,等號成立.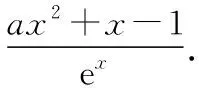

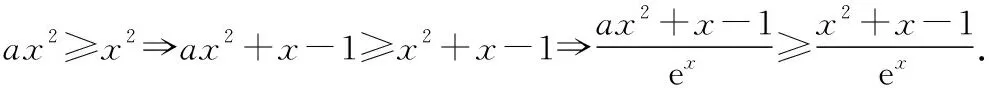
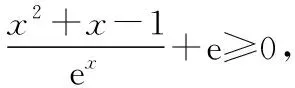
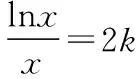
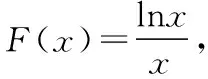
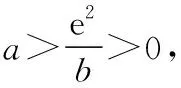
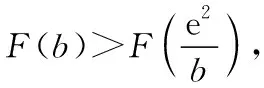
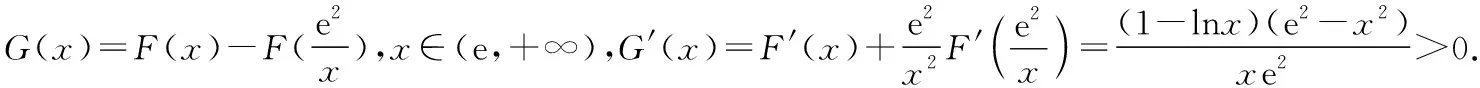
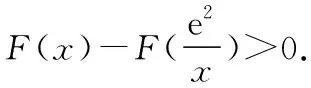
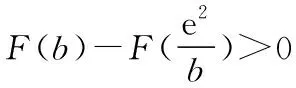
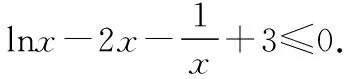
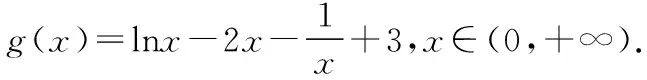
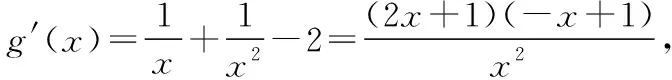
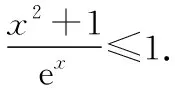
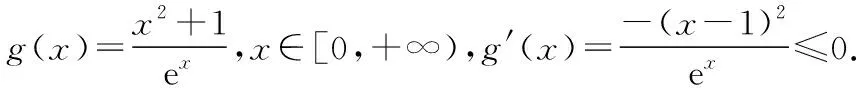
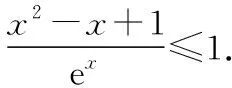
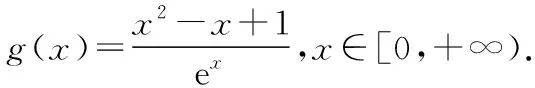
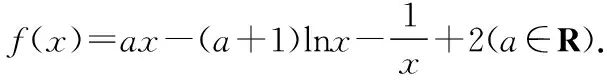
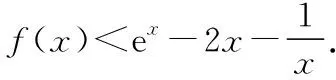
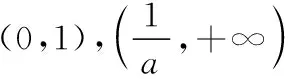
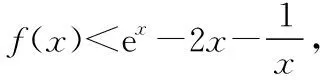
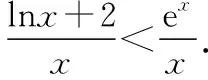
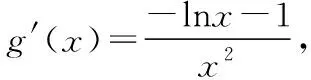
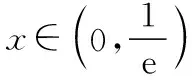
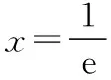
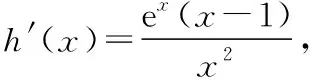
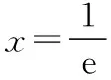
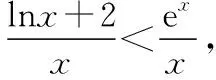
四、總結(jié)與展望