ARIMA模型探索時間序列模型在醫院急診人數預測研究中的應用

張卯紅 南京市浦口區中心醫院

1 引言

隨著時間序列應用日益增多，時間序列預測，尤其是在未來的趨勢預測。獲得越來越多的關注。實現趨勢預測的挑戰在于實時提取時間序列的趨勢特征與合理的預測模。本文回顧分析我們醫院近6年急診患者數據，應用自回歸滑動平均混合模型(ARIMA)時間序列模型方法進行分析，試圖探索預測急診患者的時間變化規律，可為管理者平衡工作量，合理安排臨床工作，實現彈性排班，優化人力資源配置，提供有益的輔助決策，同時提供如何建立相應數據模型方法步驟，供其他醫院分析參考。

2 時間序列介紹

2.1 ARIMA模型

ARIMA模型，全稱為自回歸積分滑動平均模型(Autoregressive Integrated Moving Average Model，簡記 ARIMA)，是 指 將 非 平穩時間序列轉化為平穩時間序列，然后將因變量僅對它的滯后值以及隨機誤差項的現值和滯后值進行回歸所建立的模型。該模型主要用于預測和擬合時間序列數據的趨勢，其作用是建立平穩時間序列的模型。在該模型當中，融合了移動平均模型、自回歸模型等。對于系統中過去噪聲、過去模式等方面的記憶，能夠進行分別描述。在該模型的相關系數算法中，矩方法和極大似然估計方法是其中應用較為廣泛的算法。

3 資料和方法

3.1 數據來源

通過后臺抽取2012年一2017年醫院急診患者人數，其中2012—2016年數據用于建立時間序列模型，2017年數據用于驗證所建立的模型。

3.2 研究方法

本研究采用R語言統計軟件forecast，tseries包，運用ARIMA模型進行預測。ARIMA是Box-Jenkins方法中的重要時間序列分析預測模型。該模型試圖應用相應的數學模型，將預測對象隨時間推移形成的數據序列描述出來，并在該基礎上選擇合適的模型進行預測。實際運用中，首先通過平穩性和純隨機性檢驗進行序列預處理，然后確定ARIMA(p、d、q)模型中的3個參數，其中p為自回歸的階，d為差分次數的階，q為滑動平均的階，最后通過殘差序列檢驗擬合模型是否有效，并可通過最小信息量準則(Akaike information criterion，AIC)和貝葉斯信準則(Bayesian information criterion，BIC)判斷多個模型中最優模型。

3.3 數據分析

3.3.1 數據走勢情況

根據導出的2012-2016年度數據，分析數據，R命令核心代碼如下：1).ts_data2016 ＜- ts(data2016，frequency = 12，start=c(2012，1))2).ts_data2017 ＜- ts(data2017，frequency = 12，start=c(2012，1))3).plot(ts_data2017， main=" 急診 人 數季度 走 勢圖 "， ylab=" 人數 "， xlab="時間 ")

從運行結果可以看人數逐年增長說明具有明顯趨勢性，為非平穩時間序列，需要進行差分平穩化，將非平穩時間序列轉化為平穩時間序列。先使用diff()函數對時間序列作一階差分，再使用tsdisplay()函數來觀察。基本圍繞了0在振動，基本平穩。進一步使用adf檢驗，看一下是否存在單位根（驗證平穩性，若存在則不平穩），單位根檢驗通過(P=0.01＜0.05，顯著拒絕存在單位根)。形成(1，1，0)、(8，1，0)然后判斷一下各自的AIC值，取最小值即可。

3.3.2 模型選擇

平穩化過后，要根據時間序列模型的識別規則，對平穩序列建立相應的模型。在實際的分析過程中，我們主要通過forecast中的Auto.arima()函數來快速選擇恰當的ARIMA模型，節省圖形判斷階數的主觀選擇的，顯示更為客觀準確。

根據 BIC 準則，Auto.arima 提供的最佳模型為 (0，1，1)(0，0，1)[12]，同時測試兩個模型，看看預測的結果。首先進行擬合， 然后使用tsdiag()函數看一下兩個模型的結果。兩個ARIMA模型都采用極大似然方法估計，ARIMA(0，1，1)(0，1，1)

[12]：AIC = 707.4；ARIMA(0，1，1)(0，0，1)[12]： AIC= 885.29；fit1圖中表明殘差標準差基本都在[-1，1]之間，殘差的自回歸都為0（兩虛線內）， Ljung-Box檢驗的p值都在0.05之上，而且第一模型 AIC 值比第二個模型要小，因此選擇模型 ARIMA(0，1，1)(0，1，1)[12]。

3.3.3 模型建立、預測及檢驗

根據參數估計得到的時間序列模型，我們可以對未來的序列值進行預測，并通過forecast()函數來實現，R核心代碼如下：

模型預測2017年月度實際患者人數與模型預測值比較。模型預測值的動態趨勢與實際情況基本一致，各月實測值均位于預測值95%可信區間范圍。可以看出，實際增長值與預測的最高值基本吻合，說明我們急診科患者人數正在快速增長，需要根據情況增派醫護人員。

3.4 預測

通過上面建立好的模型，我們對2018年急診患者人數做趨勢預測。

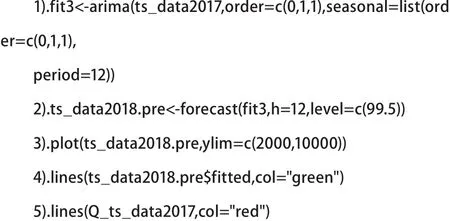
模型預測2018年月度急診患者人數，最高值達到九千人以上，把2018年1至6月份的實際急診患者人數與之對比，數據相差無幾，說明模型準確性很高。

4 討論

本研究利用2012—2017年急診患者數據，分別擬合了ARIMA(0，1，1)(0，1，1)[12]模型，并分析預測 2017 年的急診患者人數情況，發現預測值與實際值較為吻合，可以應用該模型可以對2018年急診患者人數進行預測。在實際應用中，由于所建模型是以歷史監測數據序列為依據而建立的，因此需不斷用新的監測數據對所建模型進行修正，以提高模型預測的精確度。

綜上所述，時間序列分析可應用于臨床，為資源和人員配置提供數據支持。通過對急診患者數據短期預測，可以為今后急診科合理安排臨床工作，實現彈性排班，優化人力資源配置，提供有益的輔助策。如果想更好的服務臨床工作，我們可以對數據進行細分，比如按科室統計、按時間段統計、按節假日統計，然后再進行預測，可能更好的服務于臨床工作，更能合理實現彈性排班。此分析方法也可應用到全院各個病區，對醫院做好整體規劃提供理論支持、更合理安排醫療資源，有利于醫院人員和物資的配備及調整。但使用的同時應考慮到，任何模型都有其局限性，再結合專業特點及其他影響急診人數的因素進行綜合分析。隨著醫療衛生數據快速增長，如何從醫療大數據中發掘價值以服務于領導決策將是未來區域衛生信息化研究的重要方向之一 。