Bootstrap方法在統計推斷中的應用

尤亦玲 廣東財經大學

一、背景

統計推斷是從樣本出發推斷相應的總體, 可以分為參數法和非參數法。早期的統計推斷是以大樣本為基礎的。自1908年，英國統計學家威廉·戈塞特（Willam Gosset）發現了t分布后，就開啟了針對小樣本的研究。1920年，費希爾（Fisher）提出了“似然（likelihood）”的概念，為世人提供了一種更為高效的統計推斷思維方法。1979年，美國斯坦福大學統計學教授Efron，提出了一種新的增廣樣本系統的方法，為解決小樣本的評估問題提供了新的思路，這種方法就是Bootstrap方法，也叫自助法。

統計學中“Bootstrap”法是指從原樣本自身的數據中不斷重復抽樣，從而獲得新的樣本及統計量。它的優勢在于根據給定的原始樣本復制觀測信息，因而不需要進行分布假設或增加新的樣本信息就可以可對總體的分布特性進行統計推斷，屬于一種非參數統計方法。

二、方法理論介紹

（一）Bootstrap重抽樣理論

Bootstrap重抽樣的基本思想是：在原始數據的范圍內作等可能的、有放回的再抽樣, 樣本容量仍為n，原始數據中每個樣本每次被抽到的概率均為1/n , 我們將這種抽樣方法所得的樣本稱為Bootstrap樣本。每次抽樣可得到參數的一個估計值，這樣重復若干次。

設隨機樣本是獨立同分布的，。假設為總體分布F的某個參數，是觀測樣本的經驗分布函數，是的估計，則可以通過以下步驟來實現Bootstrap估計：

第一步，對Bootstrap重復的第b次(b=1,2,…,B），先有放回地從中抽樣得到再抽樣樣本,然后根據計算；

第二步，的Bootstrap估計為的經驗分布函數。

（二）Bootstrap方法的標準差、偏差估計

估計量的標準差的自助法估計，是Bootstrap重復的樣本標準差：

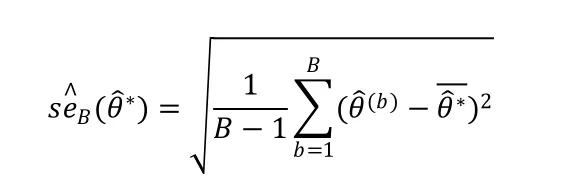
其中。我們將估計量的偏差定義為

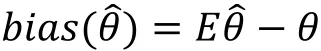
事實上，根據上式計算偏差有一個很明顯的難點在于，當的分布未知，或者形式很復雜時，期望的計算也就變得很困難甚至不可能，因此在這種情況下偏差就是未知的。但是當我們擁有樣本數據時，就是的一個估計，而期望可以通過Bootstrap方法進行估計，從而得到偏差的估計：

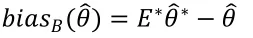
表示Bootstrap的經驗分布。

可見，一個估計量的Bootstrap偏差估計，就是通過已有樣本的估計量來代替，并使用的Bootstrap重復來估計。對一個有限樣本，有的B個獨立同分布的估計量,則的均值是期望的無偏估計，因此偏差的Bootstrap估計為

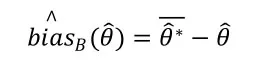
其中。若偏差為正，則說明在平均水平上過高估計了，反之，則說明在平均水平上低估了。因此，可以對估計量進行偏差修正，得到

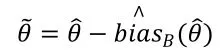
（三）Bootstrap區間估計的四種類型

1.標準Bootstrap

假設是參數的估計量，它的標準差為。如果的分布服從或近似服從正態分布，那么，當顯著性水平為，并且是的一個無偏估計時，就有的（1-）標準正態Bootstrap置信區間為

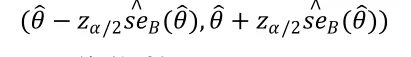
2.百分位數Bootstrap

該方法的核心在于：統計量在（1-）水平下的置信區間的上下限，分別為估計量的Bootstrap經驗分布的第和第（）分位點。

事實上，可以對百分位數區間做進一步修正，得到更好的Bootstrap置信區間，使其具有更好的理論性質和實際覆蓋率。其原理是對（1-）水平下的置信區間，使用兩個因子來調整和（）分位數，其一為對偏差（bias）的修正，另一個是對偏度（skewness）的修正。前者記為，后者記為a。我們將這種估計方法估計的結果稱為更優的Bootstrap置信區間，簡稱為BCa。

在計算（1-）BCa置信區間時，首先計算Bootstrap重復經驗分布函數的分位數，即BCa區間的上下界，則上述中的偏差修正因子的估計為

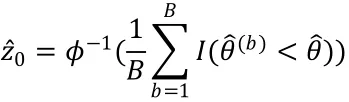
而加速因子是從Jackknife重復中估計得到的。

3.基本Bootstrap

在的分布未知時，由于Bootstrap重復下的樣本分位數滿足

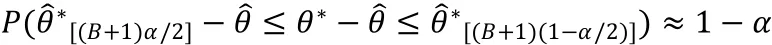
因此，（1-）置信區間為

4.t區間Bootstrap

在多數情況下，即使滿足正態分布假設，且是的一個無偏估計時，也未必服從正態分布，這是因為是我們認為估計出來的。同時，由于Bootstrap估計的分布是未知的，因此也不能認為Z服從t分布。在這種情況下，前人就通過再抽樣的方法得到了一個“t類型”的統計量的分布，以此來改進標準Bootstrap區間估計。

假設觀測樣本，則（1-）水平下的Bootstrap t置信區間為：

根據以往的設計經驗來看，城市居民供水系統多會采取管道分流方式，從城市給水系統中分流至各大住宅小區當中，目的在于及時供給人們日常飲用水源。針對于此，建筑施工單位在進行給排水設計過程中，需要在住宅小區的管道處安裝倒流防止閥裝置，這樣做的主要目的在于避免水流出現嚴重的倒流問題，造成供水壓力的明顯提升。

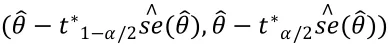
其中通過以下方法得到：

第一步，計算觀測到的；第二步，從X中有放回地抽樣得到第b個樣本，從中再抽樣計算得到,以及Bootstrap標準差估計，據此可以計算第b個重復下的“t”統計量；第三步，重復上述過程，將的分布作為推斷分布，找出樣本分位數；第四步，根據Bootstrap重復可得標準差估計；第五步，計算置信區間。

從上述計算過程可以發現，Bootstrap t區間法需要進行Bootstrap嵌套，嚴重影響了計算速度。

三、方法分析討論

（一）Bootstrap重抽樣法的應用

假設我們觀察到一組樣本，從中再抽樣，依照抽到1,2,3,4,5的概率分別為0.2，0.3，0.2，0.1，0.2 進行。因此，從中隨機選擇的一個樣本，其分布函數就是經驗分布函數。 事實上，樣本可以看作是從Poisson(2)中隨機產生的，因此利用R軟件我們可以實現對的估計，并與Poisson(2)的分布相比較，結果如下：

圖3.1 Bootstrap重抽樣的估計

（二）標準差、偏差的Bootstrap估計

R軟件中bootstrap程序包里的law82數據集，記錄了美國82所法律學校入學考試的平均成績（LSAT）和GPA,估計二者之間的相關系數，并求樣本相關系數的標準差和偏差的Bootstrap估計。

對于成對數據可以通過樣本相關系數估計相關系數，計算結果顯示，樣本相關系數為0.80，使用bootstrap方法估計的標準差的結果。

此外，在重復2000次下的boot函數計算的標準差估計為0.05，該結果與之前的結果相差無幾。同時，boot函數還給出了該組數據的樣本相關系數bootstrap偏差估計，其結果為-0.000727641。

通過偏差的定義自行編程進行求解，得到的結果bias=-0.0009563065，與boot函數的運算結果非常接近。

（三）Bootstrap區間估計

繼續針對上述law82數據集討論相關系數統計量的95%置信區間，利用boot包里的函數boot.ci可以直接計算得到基本bootstrap區間、標準正態bootstrap區間、百分位數bootstrap區間和BCa區間。我們還可以根據Bootstrap t區間法的定義，利用自編函數來計算相關系數置信區間，結果如下表所示：

表3.1 law82相關系數統計量bootstrap置信區間估計結果

由上表結果可以看出，前兩種估計方法和后三種方法的結果有較大差異，而在后三種方法中，可以看到BCa置信區間的區間長度是最小的，可以認為它的估計是較為準確的。

四、實際數據

考慮bootstrap包里的scor考試成績數據，利用pairs函數繪制每對變量的散點圖，觀察相關性。

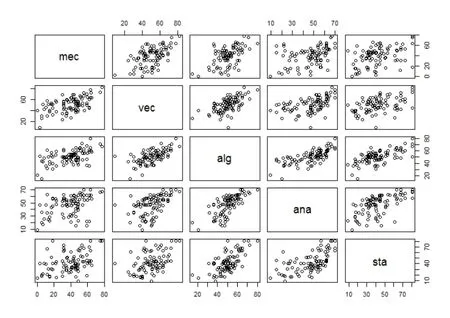
圖4.1 scor數據集各變量散點圖

根據上圖所示結果，我們可以猜測(mec,vec),(alg,ana),(alg,st a),(ana,sta)這四組變量間可能具有較強的相關性，利用R軟件計算其相關系數分別為0.55，0.71，0.66，0.61，利用Bootstrap估計樣本相關系數標準差。

表4.1 四組變量相關系數的Bootstrap標準差估計結果

在scor數據下，記協方差矩陣為，其特征根為 ，則

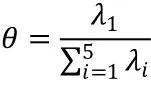
表示了主成分中第一主成分對方差的解釋比例。現令為樣本協方差矩陣的特征根，可以利用boot函數直接得到的Bootstrap偏差和標準差估計，程序運行結果顯示的偏差為0.0022，標準差為0.0472。

利用Bootstrap重復樣本，對的95%置信區間，分別采用百分位數和修正的百分位數Bootstrap置信區間進行估計，并更改重復次數觀察結果，如下表所示：

表4.2 的95%置信區間估計結果

由上表可知，不同的模擬次數會對置信區間的結果造成一定的影響，但總體來說差別不大。

五、總結

本文基于對Bootstrap統計推斷方法的理論介紹，利用實際案例實現了在總體分布未知情況下，對樣本統計量的標準差、偏差估計，以及置信區間估計。其核心思想在于重復抽樣，應用的關鍵在于理解“子樣本之于樣本，等于樣本之于總體”，優勢之處在于小樣本增強。總的來說，Bootstrap是一種應用十分簡便的非參數統計推斷方法。