非均勻外擠壓載下套管擠毀界限的仿真研究
李增亮,杜明超,李昆鵬,張 峰,張瑞霞
(1.中國石油大學(華東)機電工程學院,山東 青島 266580;2.勝利油田石油工程技術研究院,山東 東營 257000)
1 引言
目前,由于油田開發已進入中后期,深埋井下的套管經過長時間的服役,已逐漸出現不同程度、類型的損壞。雖然各油氣開發生產單位普遍認識到套損井治理在恢復老油田穩產基礎和提高老油田綜合經濟效益方面的作用和意義,但目前套損井治理工作仍然零散運行,沒有形成系統化和規模化,套損井逐年增加的趨勢未能得到有效控制[1]。非均勻外擠壓力是致使套管損傷的一個重要因素,通過開展非均勻外擠壓力作用下套管的擠壓行為和擠毀界限的研究,明確套管所承受擠壓變形的能力,能夠有效的降低修井成本、提高油井采油量。近年來許多專家學者對此進行了相關研究,李子豐等人[2]研究表明如果地層不具有蠕變性,地應力不會作用在套管上;如果地層具有蠕變性,且持續時間比較長時,套管所受的外擠載荷為地層的上覆巖層壓力。但是隨著油井的使用年限增加,井壁周圍的疏松地層難免會發生坍塌、掏空等現象,從而使套管更易承受非均勻外擠載荷的影響。房軍等人[3]分析發現隨地應力非均勻程度的增加,套管形變經歷了由兩向擠壓-擠壓到兩向拉伸-擠壓組合方式的轉變;夏雪梅等人[4]對承受單向外擠載荷的承載能力及其變形損壞進行了仿真研究;蔡正敏等人[5]對非均勻地應力下具有初始橢圓度的套管強度進行了分析。但是這些研究都未明確非均勻外擠壓力及外載不均勻度與套管擠毀界限的關系。為此,筆者就非均勻外擠壓力作用下套管的擠毀界限進行詳細的分析與闡述。
2 彈塑性有限元模型建立
根據套管的實際變形情況,做出如下假設:①套管的初始橢圓度為零(即套管完好無損毀);②水泥環、套管為均勻壁厚圓筒,且與井眼中心同心;③軟地層、水泥環、套管均為各向同性材料;④套管和水泥的接觸邊界為完全接觸[6]。
套管一般下入幾千米深的地層內,由于巖層一般較厚,根據厚壁圓筒理論,將此問題處理成平面應變問題加以分析,因此依照上述假設建立分析模型,在套管變形井段取某一橫截面進行套管擠壓變形研究。
水泥環和巖層材料的本構關系均采用Drucker-Prager彈塑性本構模型。D-P本構模型是理想彈塑性模型,它綜合了胡克定律和Coulomb破壞準則,并且采用更適用于數值計算的圓錐形屈服面函數。其中涉及到5個參數,即控制彈性行為的彈性模量和泊松比,以及控制塑性行為的粘聚力、內摩擦角和膨脹角。膨脹角是用來衡量體積膨脹大小的標度,在巖石工程中,一般密實的砂土和超強固結土在發生剪切作用的時候由于顆粒的重新排列會發生體積膨脹,而一般的巖石或者正常固結的土體,只發生剪縮[7]。因此在本文中,將膨脹角設置為0°比較符合實際工況。
套管——水泥環——地層整體有限元計算模型如圖1所示,模型整體采用Plane82單元,套管與水泥環、水泥環與地層之間分別選用TARGE169單元和CONTA172單元來建立接觸,保證力傳遞的連續性。根據巖石力學和彈塑性力學理論,不考慮套管所承受的內壓,在平面無限遠受Y方向壓力為σh,X方向壓力為σH,當地層邊界超過井眼半徑的5~6倍以后,對井周應力的影響很小,可忽略不計,所以本模型中地層寬度取為井眼直徑的20倍[8],在保證求解精度的前提下,減少有限元計算時的節點和單元總數,能夠明顯提高計算效率[9],此外,考慮到模型的對稱性,取1/4進行分析,并施加對稱約束。套管常用的鋼級及其相應的材料參數、水泥環參數及地層參數均來源于油田現場提供的生產數據和試驗數據,研究中選取鋼級為N80的5.5in×7.72mm、5.5in×9.17mm、7in×9.19mm和7in×12.65mm套管進行仿真分析。具體的套管、水泥環、地層的力學參數如表1所示。
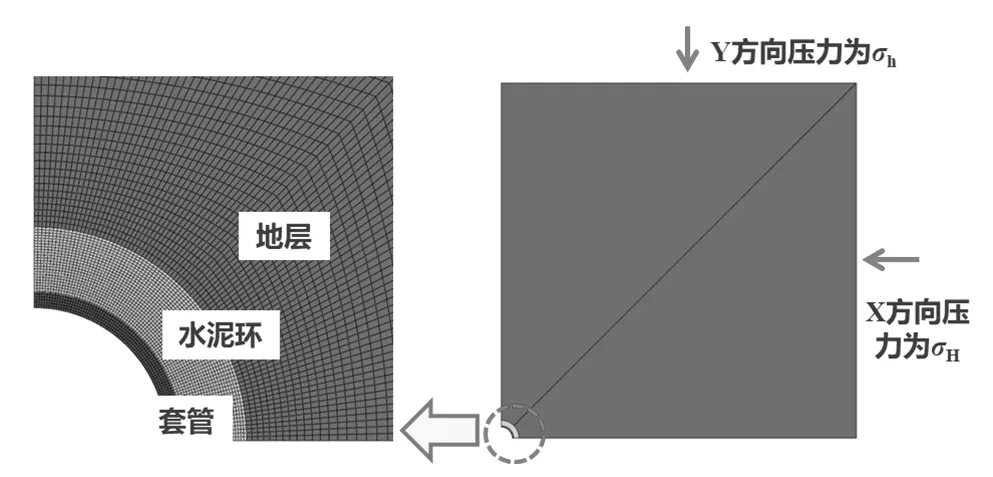
圖1 套管非均勻受載有限元模型

表1 套管、水泥環和地層的力學參數
3 結果及分析
本文主要以鋼級為N80,外徑為139.7mm壁厚為7.72mm的套管的仿真求解結果為例進行詳盡的分析與說明。
3.1 5.5in×7.72mm套管的擠毀界限研究
為了研究套管在非均勻外擠壓力作用下的縮徑變形規律,分析中選取不同大小的σH和σh的進行配比組合,但始終保證σH>σh。在計算過程中,將套管模型的最大變形量定義為在該外載情況下套管的最大縮頸,當出現導致數值分析計算結果發散的幾何大變形時,則認為套管徹底損壞,同時將前一外載組合作用下套管的最大縮頸定義為套管在該外載情況下的擠毀界限。當Y方向擠壓力σh大于75MPa或小于25MPa時,其數值分析結果和75MPa及25MPa相差不大,因此選取25,35,45,55,65,75MPa作為Y方向擠壓力σh進行具體分析。不同Y方向擠壓力所對應的X方向擠壓力取到極限時套管最大縮頸如表2所示。
表2表明,外徑13.9mm壁厚為7.72mm的套管在Y方向擠壓力為25MPa,X方向擠壓力135MPa時,其擠毀界限為11.85mm;但當Y方向擠壓力為75MPa,X方向擠壓力384MPa時,其擠毀界限為66.6mm。通過對比數據可以發現,套管在地層壓力作用下的擠毀極限并不是一個定值,而是隨著外載的不同發生改變。

表2 X方向擠壓力取到極限時套管最大縮頸
為了明確在不同外載條件下套管的擠毀界限,將Y方向擠壓力作為自變量,套管的擠毀界限作為因變量進行數值擬合,得到如下公式:
y =-5.729×10-6x4+ 0.001698 x3-0.1678 x2+7.659 x-99.19
(1)
其中,x-Y方向擠壓力/MPa;y-套管擠毀界限/mm。
該公式的SSE(誤差平方和)為3.395,R-Square(確定系數,越接近1,表明方程的變量對y的解釋能力越強,模型對數據的擬合也較好)為0.9982。通過測量Y方向(變形長軸方向)的外載壓力,代入上述公式,便可求得在該壓力下套管的擠毀界限。
筆者認為,套管的擠毀極限之所以會隨著外載的不同而發生變化,是因為X方向和Y方向的擠壓力相差過大所致。為更加明確的闡述套管雙側變形損壞的機理,同時減小上述方程的誤差,引入外載不均勻度進行分析。
外載不均勻度定義為x方向外擠壓力于y方向外擠壓力的比值(以下均稱為不均勻度)。
套管達到擠毀界限時所對應的極限不均勻度如表3所示。
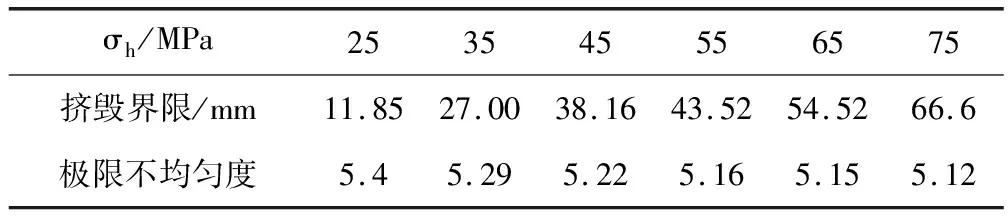
表3 套管擠毀界限所對應的極限不均勻度
從上表中可以發現,外徑為139.7mm壁厚為7.72mm的套管在外載不均勻度為5.12~5.4的范圍內時會發生擠毀,且該套管所能承受的極限不均勻度隨外載的增加而降低。
將Y方向擠壓力和該壓力作用下的極限不均勻度進行數值擬合,得到曲線圖2所示:
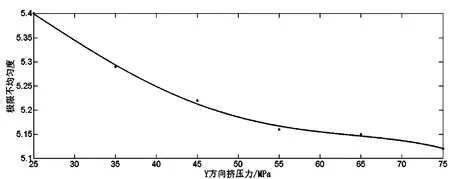
圖2 Y方向擠壓力-極限不均勻度擬合曲線
方程為:
b=-8.333×10-8a4+ 1.5×10-5a3-0.0008292 a2+ 0.007554 a + 5.52
(2)
式中,a-Y方向擠壓力/MPa,b-極限不均勻度;
誤差平方和SSE:0.0001286;確定系數R-Square:0.9977。
再將極限不均勻度和擠毀界限進行數值擬合,得到如下曲線:
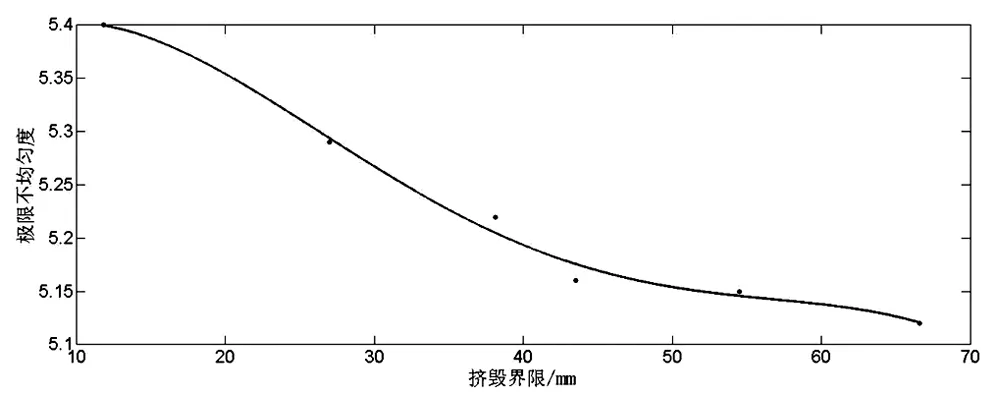
圖3 套管最大縮頸-極限不均勻度擬合曲線
方程為:
b=-1.313×10-7c4+2.185×10-5c3-0.001177 c2+0.01719 c+5.327
(3)
式中,c-套管擠毀界限/mm;
誤差平方和SSE:0.0005107;確定系數R-square:0.9908。
將測得Y方向擠壓力代入公式(2)求得該壓力作用下的極限不均勻度,然后用公式(3)求得該壓力作用下的擠毀界限。公式(2)和(3)的誤差平方和分別為0.0001286、0.0005107,和公式(1)的SSE相比小很多,因此通過加入不均勻度來求解套管擠毀極限縮頸可以很好的減小擬合誤差。
3.2 5.5in×7.72mm套管的最佳修井尺寸
應力-應變曲線的形狀反應材料在外力作用下發生的彈性、屈服、塑性、斷裂等各種形變的階段。套管在非均勻外擠壓力的擠壓下同樣會發生類似的形變過程,即由彈性階段到屈服階段,再到塑性階段,最后發生擠毀壓潰現象。現將數值模擬得到的套管縮頸量和套管內部的最大應力進行曲線擬合,得到5.5in×7.72mm套管在不同外載作用下的應力-應變曲線。圖4為Y方向擠壓力25MPa套管應力-應變曲線。
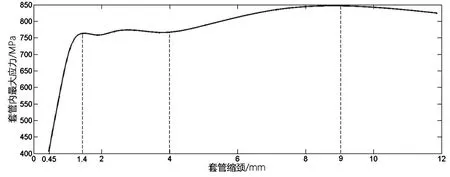
圖4 Y方向擠壓力25MPa套管應力-應變曲線
從圖線中可以看出,縮頸量在0.45mm到1.3mm范圍內時,曲線大部分為一條偏離縱軸的斜直線,表示套管內部應力與縮頸量成正比,服從虎克定律,套管進入彈性階段。套管縮頸量在1.3~4mm時,圖線變為一條具有小幅度波動的線段,此時應力幾乎不增長,但是套管縮頸卻迅速增加,套管進入屈服階段。套管縮頸量在4 ~9mm時,圖線為一條上彎曲線。這表明套管經過屈服階段之后,又恢復了抵抗擠壓變形的能力,如果要使其繼續變形,必須增大外擠壓力。當套管縮頸達到9mm時,套管內最大應力達到峰值,即套管的抗壓強度846MPa。隨后套管縮頸在9~11.85mm時,套管內部應力集中處發生應力釋放,如圖5、圖6所示,Y方向擠壓力25MPa、X方向擠壓力130MPa時套管內的最大應力為846MPa,Y方向擠壓力25MPa、X方向擠壓力135MPa時套管最大應力為825MPa。說明此時套管局部已經發生破壞,縮頸量增加,等效應力逐漸降低,最后發生擠毀。
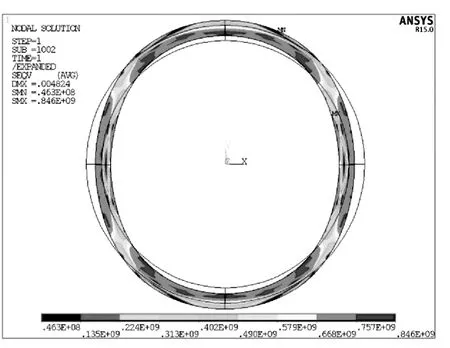
圖5 Y方向擠壓力25MPa、X方向擠壓力130MPa套管應力云圖
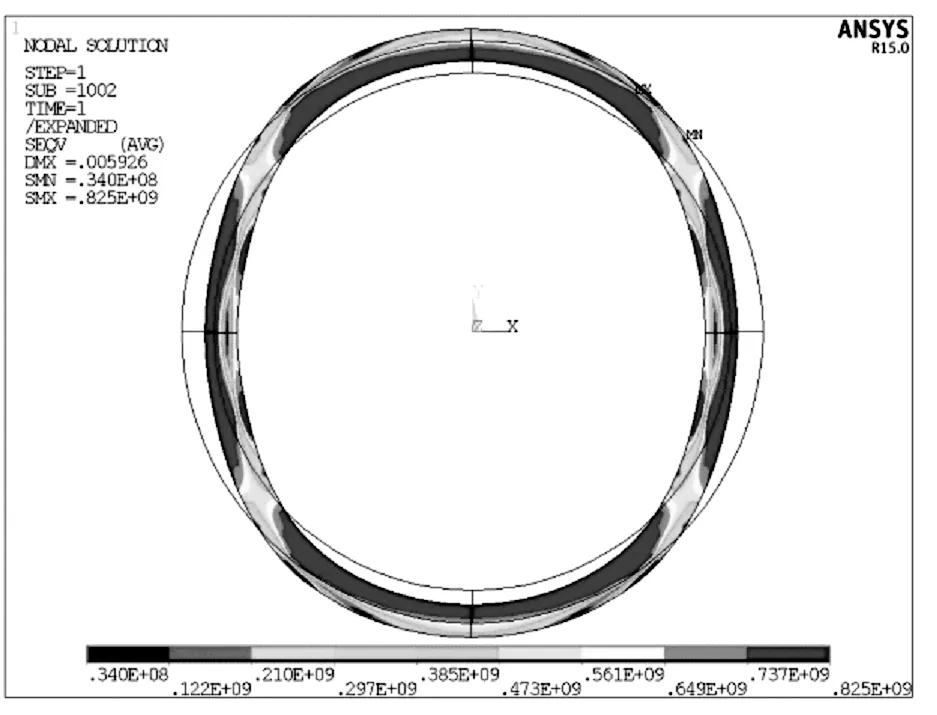
圖6 Y方向擠壓力25MPa、X方向擠壓力135MPa套管應力云圖
當Y方向擠壓力≥45MPa時,隨著外載的增大,套管進入彈性階段的時間逐漸減小,且當縮頸達到9mm時,套管內的最大應力并未達到整個過程的最大值。然而在縮頸量超過該臨界點之后,套管內的最大應力并不隨著最大縮頸的增大而減小,而是發生了不規則震蕩。隨著Y方向擠壓力的增大,震蕩的幅度和頻率也增大。圖7為Y方向擠壓力55MPa套管應力-應變曲線。
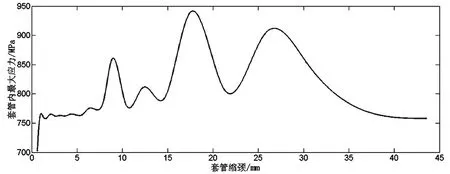
圖7 Y方向擠壓力55MPa套管應力-應變曲線
綜上所述,5.5in×7.72mm套管的變形量為9mm時是一個臨界點。在這個臨界點之前,套管仍然具有抵抗變形的能力,但變形量超過9mm,套管內部或出現應力釋放現象,或出現套管內應力隨形變量增大而不規則震蕩現象,兩種現象都可能表明套管已經發生局部破壞。該種條件下即使修復其抵抗二次擠壓的能力也大大降低。因此,將9mm定義為5.5in×7.72mm套管在非均勻外擠壓力力作用下的最佳修井尺寸。
為得到套管縮頸量和不均勻度之間的關系,將不同外擠壓力擠壓下的套管縮頸和其所對應的不均勻度擬合曲線,如圖8所示。

圖8 5.5in×7.72mm套管不均勻度-套管縮頸擬合曲線
該曲線表明,外載不均勻度小于3.5時,最大縮頸隨不均勻度的增大而近乎線性增大,當不均勻度大于3.5時,最大縮頸隨不均勻度的增大呈現類似拋物線增大。應力-應變曲線發生震蕩最劇烈的位置是在由線性向拋物線轉換的階段,即3.5~4.5范圍內。
4 結論
(1)通過對比X方向外擠壓力取極限值時套管的最大縮頸可知,套管的擠毀界限并不為定值,而是隨外部載荷的增加而增大,并給出了表述兩者關系的擬合方程。
(2)當Y方向擠壓力大于25MPa時,套管的擠毀界限之所以會隨著外載的不同而改變,是因為X方向和Y方向的外擠壓力相差過大所致。外徑為139.7mm壁厚為7.72mm的套管在Y方向大于等于25MPa的情況下,在外載不均勻度達到5.12~5.4的范圍內時,便會發生擠毀,且該套管承受的極限不均勻度隨外載的增加而降低。
(3).在求解5.5in×7.72mm套管在非均勻外擠壓力的擠壓下的擠毀界限時,通過引入外載不均勻度作為變量,能夠很好的減小擬合誤差,增大求解精度。
(4).從套管受不均勻外擠壓力擠壓的角度分析,將縮頸9mm定義為5.5in×7.72mm套管的最佳修井尺寸。不均勻度小于3.5時,套管縮頸量隨不均勻度的增大而近乎線性增大,當不均勻度大于3.5時,套管縮頸量隨不均勻度的增大進行類似拋物線增大。應力-應變曲線發生震蕩最劇烈的位置是在由線性向拋物線轉換的階段。

