車載LNG氣瓶在高溫下熱力學參數的變化研究*

楊 剛，黃 思，李 蔚，易天坤，譚 粵

（1.廣東省特種設備檢測研究院，廣東佛山 528000；2.華南理工大學機械與汽車工程學院，廣州 510641）

0 引言

液化天然氣（LNG）作為一種清潔能源，以其低碳環保的特點用于汽車燃料[1]。汽車上的LNG燃料系統由氣瓶、汽化器、減壓閥等組件組成。LNG 在低溫氣瓶內以液態形式儲存，隨著外界熱量的傳遞使得氣瓶內LNG 產生蒸發，壓力也隨之增高。當氣瓶內部壓力達到臨界壓力時，減壓閥將自動開啟降低壓力以保證氣瓶安全[2]。

近年來，國內外學者相繼開展了LNG 儲罐內部熱力學參數變化的研究。Miana 等[3]通過物理算法和“智能”模型研究了船用LNG 儲罐運輸到目的地的物性參數的改變；Chen 等[4]對常溫下車載LNG 氣瓶內的漏熱和壓力變化進行了分析計算；Khemis 等[5]采用數值方法對盛裝LNG 的低溫儲罐，使用FLUENT 軟件進行了傳熱分析，得到低溫儲罐頸部氣體的溫度和速度；李玉星等[6]研究了LNG為介質密閉儲罐，進行了儲罐內物性參數測試實驗，證實了儲罐內的溫度場是非均勻的；肖時雄等[7]對LNG船儲液罐在運輸過程中常溫狀態下的傳熱及升壓過程進行了研究；謝高鋒[8]和王貴仁[9]對LNG儲罐內壓力變化進行了實驗研究，并編制了低溫儲罐無損儲存規律的程序來計算儲罐內物性參數隨時間的變化規律。

上述研究主要集中在LNG 儲罐內在常溫下的熱力學參數研究，缺乏燃燒高溫下氣瓶內部熱力學參數變化的研究。因此，本文選取一種常用的車載LNG氣瓶作為研究對象，在高溫環境下對該氣瓶進行傳熱學計算分析，得到LNG熱力學參數隨時間的變化規律，為車載LNG氣瓶的安全問題提供技術支持。

1 計算模型和計算方法

1.1 物理模型

圖1 所示為365 L 型車載LNG 氣瓶的計算模型。該車載LNG氣瓶為多層保溫結構；表1所示為氣瓶的操作參數；表2所示為各層材料的導熱系數，其中真空層的導熱系數λ3由實驗測得。

1.2 計算方法

由于所研究的LNG 氣瓶容積較小，介質較快達到熱平衡，不容易形成溫度分層，因此采用飽和均質模型對氣瓶進行傳熱計算。根據熱力學定律在Δt時間內有如下關系[10]：

圖1 車載LNG氣瓶結構簡圖

表1 365 L型車載LNG氣瓶基本參數

表2 365 L型車載LNG氣瓶物性參數

式中：Q為氣瓶吸收的熱量；cpl為液態比熱；cpg為氣態比熱；ml為液態質量；mg為氣態質量；ΔT為Δt時間間隔前后氣瓶內溫差；Φ 為漏熱率。

LNG 的主要成分是甲烷，根據甲烷在飽和狀態下的熱力學關系[11]，在-165～-105 ℃溫度范圍內擬合出液態比熱cpl、氣態比熱cpg、壓力p和汽化潛熱r與溫度T的關系為：

為計算氣瓶的漏熱率Φ 作出如下假設：（1）漏熱量只考慮以熱傳導的方式，且全部被氣相和液相主體所吸收；（2）整個氣瓶的傳熱方向為保溫層的法線方向，氣瓶總熱阻是多個保溫薄層熱阻的疊加。

該氣瓶漏熱主要有圓筒體Φ1和封頭Φ2[12]：

則總的漏熱率為：

其中：

式中：D1為圓筒內徑；D2為圓筒外徑；D3為圓筒保溫層內徑；D4為圓筒保溫層外徑；D5為外殼筒體內徑；D6為外殼筒體外徑；為封頭內徑；為封頭外徑；為封頭保溫層內徑；為封頭保溫層外徑；為外殼封頭內徑；為外殼封頭外徑；L為內圓筒長度；l為外殼筒體長度；Ts為氣瓶外環境溫度，℃；

將式（5）代入式（1）得到如下關系式：

采用向前差分的方法將式（7）進行離散，對該式左邊溫度T采用初始溫度Ti和終了溫度Ti+1的平均值計算：

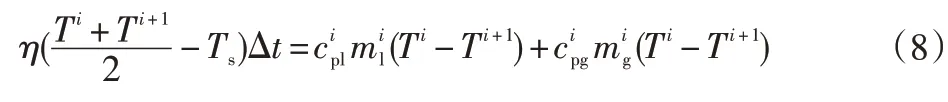
由式（8）可得氣瓶內介質終了溫度Ti+1的表達式為：

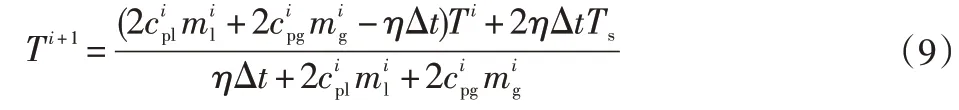
因此，終了的蒸發率αi+1、氣態介質質量和液態介質質量有如下關系[13]：

已知條件有氣瓶容積V，充裝率φ和環境溫度Ts等，初始條件為：

因為氣瓶安全閥的起跳壓力為1.6 MPa，因此當氣瓶內壓力達到這個壓力值時計算終止，計算流程如圖2所示。該計算方法得到了液氮實驗數據[14-15]的驗證。

圖2 方法計算流程圖

2 計算結果分析

選取3個代表性的環境溫度Ts如夏天的室外高溫40 ℃[16]、天然氣著火的最低溫度270 ℃和城市煤氣燃燒的最高溫度600 ℃[17]，來研究車載LNG氣瓶內物性參數隨時間的變化規律。

2.1 LNG質量和時間的關系

隨著外界熱量的傳遞，使得氣瓶內LNG產生蒸發，所產生的蒸發氣（BOG）質量不斷增加。圖3所示為計算得到的無量綱LNG 質量隨時間t 的變化曲線。由圖可知，氣瓶內LNG質量ml隨著時間呈現下降趨勢。當環境溫度Ts增加時，LNG蒸發加快。在絕熱層未損壞時，LNG蒸發較慢。

圖3 LNG質量和時間的關系

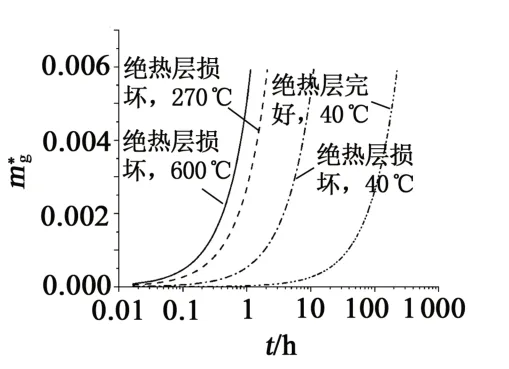
圖4 BOG質量和時間的關系

2.2 氣瓶內介質溫度和時間的關系

圖5 所示為計算得到的氣瓶內介質溫度T 隨時間t 的變化曲線。由圖可知，從初始狀態到氣瓶最大工作壓力這一過程，介質溫度T從-161 ℃上升到了-113.15 ℃左右。介質溫度T在初始階段上升較慢，隨著LNG的不斷蒸發，溫度T上升的速度增快。當環境溫度Ts增加時，介質溫度T 上升速率增快。在絕熱層未損壞時，介質溫度T上升速率較慢。

圖5 氣瓶內介質溫度和時間的關系

圖6 介質壓力和時間的關系

2.3 氣瓶內介質壓力和時間的關系

圖6 所示為計算得到的氣瓶內介質壓力p 隨時間t 的變化曲線。由圖可知，介質壓力p 在初始階段上升速度較慢，隨LNG 的不斷蒸發，介質壓力p 上升速度增快。當環境溫度Ts增加時，瓶內的升壓更快。此外，在絕熱層完好、40 ℃的環境溫度下，氣瓶內介質壓力需要224 h達到起跳壓力；在絕熱層損壞、40 ℃環境溫度下，氣瓶內介質壓力需要11.1 h 達到起跳壓力；在270 ℃環境溫度下，氣瓶內介質壓力需要2.1 h達到起跳壓力；在600 ℃環境溫度下，氣瓶內介質壓力需要1.1 h達到起跳壓力。

3 結束語

本文以LNG為工質，選取常用的365 L規格的氣瓶進行傳熱計算，采用飽和均質模型得到了如下結論。

（1）隨著外界熱量的傳遞，使得氣瓶內LNG產生蒸發，所產生的蒸發氣（BOG）質量將不斷增加，最終達到氣瓶內介質總質量的0.59%。氣瓶內LNG質量隨著時間逐漸減少。當環境溫度增加時，LNG蒸發得更快；在絕熱層未損壞時，LNG蒸發較慢。

（2）從初始狀態到氣瓶最大工作壓力這一時間段內，氣瓶內介質溫度從-161 ℃上升到了-113.15 ℃左右。介質溫度在初始階段上升較慢，隨著LNG 的快速蒸發，其溫度上升的速度增快。當環境溫度增加時，介質溫度上升速率增快。在絕熱層未損壞時，介質溫度上升速率較慢。

（3）氣瓶內介質壓力在初始階段上升速度較慢，隨LNG的不斷蒸發，上升速度增快。當環境溫度增加時，瓶內的介質升壓更快。在絕熱層完好時、40 ℃的環境溫度下，介質壓力達到起跳壓力需要224 h；在絕熱層損壞的情況下，當環境溫度為40 ℃、270 ℃和600 ℃時，介質壓力達到起跳壓力的時間分別為11.1 h、2.1 h和1.1 h。