綁腿式高空蹦極Z向加速度的標準適用性研究*
紀永宏,宋偉科,陽先波,張 建
(1.中國特種設備檢測研究院,北京 100029;2.沈陽創意游樂管理有限公司,沈陽 110000)
0 引言
高空蹦極是近年來新興的一項非常刺激的極限運動,越來越受到青少年的歡迎。高空蹦極是指跳躍者依靠彈性繩或其他彈性件的收縮,從高空固定塔架或平臺向下跳躍。當人體落到離地面一定距離時,彈性繩被拉開、繃緊、阻止人體繼續下落;當到達最低點時,彈性繩再次彈起,人被拉起,隨后又落下,這樣反復多次直到彈性繩的彈性消失為止。高空蹦極按其束縛方式主要可分為綁腿式、綁腰式和綁胸式3種,目前綁腿式蹦極比較多[1]。
加速度是游樂設施的關鍵參數,也是重大風險源,直接涉及乘客安全[2]。高空蹦極的加速度尤其是Z向加速度一直是備受關注的研究對象,Z向加速度對人體的影響是最大的也是最多的。+Z向加速度會導致血液從頭部移動到身體下部,引起腦部與視覺器官的紊亂,隨著加速度的繼續增大,會引起短暫的視覺和意識喪失,同時還會對其他器官造成很大影響;-Z方向加速度會使血液從人體下部向頭部排出,導致血液供應紊亂,血管和顱內壓增加,伴隨著尖銳的頭疼、視力障礙及出血[3]。
美國、歐盟標準都對游樂設施加速度提出了明確要求[4-5],但高空蹦極在國外屬于極限運動,不屬于游樂設施范疇,所以游樂設施加速度要求不適用于高空蹦極。目前在中國,高空蹦極被納為受監管的無動力類游樂設施,其Z 向加速度理應滿足GB8408-2018《大型游樂設施安全規范》[6]的技術要求。本文主要對綁腿式高空蹦極的-Z 向加速度進行分析,并與GB8408規定的加速度進行比較,就高空蹦極Z向加速度與游樂設施標準的適用性進行了探討。
1 基本情況
蹦極繩一般分為重繩(紅繩)和輕繩(藍繩)兩種,紅繩承重65~90 kg,藍繩承重40~65 kg。本文以原始長度55 m蹦極繩作為研究對象,其中紅繩質量14 kg,藍繩質量12 kg。分別采用能量守恒理論和ADAMS軟件動力學仿真兩種方法對高空蹦極的-Z向加速度進行對比分析,以驗證計算結果的準確性。為了消除彈性繩自身重量的影響,本文以彈性繩自然下垂的長度位置作為拉伸起點,該方法較傳統的等效質量法更為準確。
GB8408-2018《大型游樂設施安全規范》中關于人體坐標系及Z向加速度允許值的要求如圖1所示。由圖可知,在-Z方向持續時間0.3 s內允許承受的最大加速度az=1.7g,最大允許極限加速度az=2.0g。
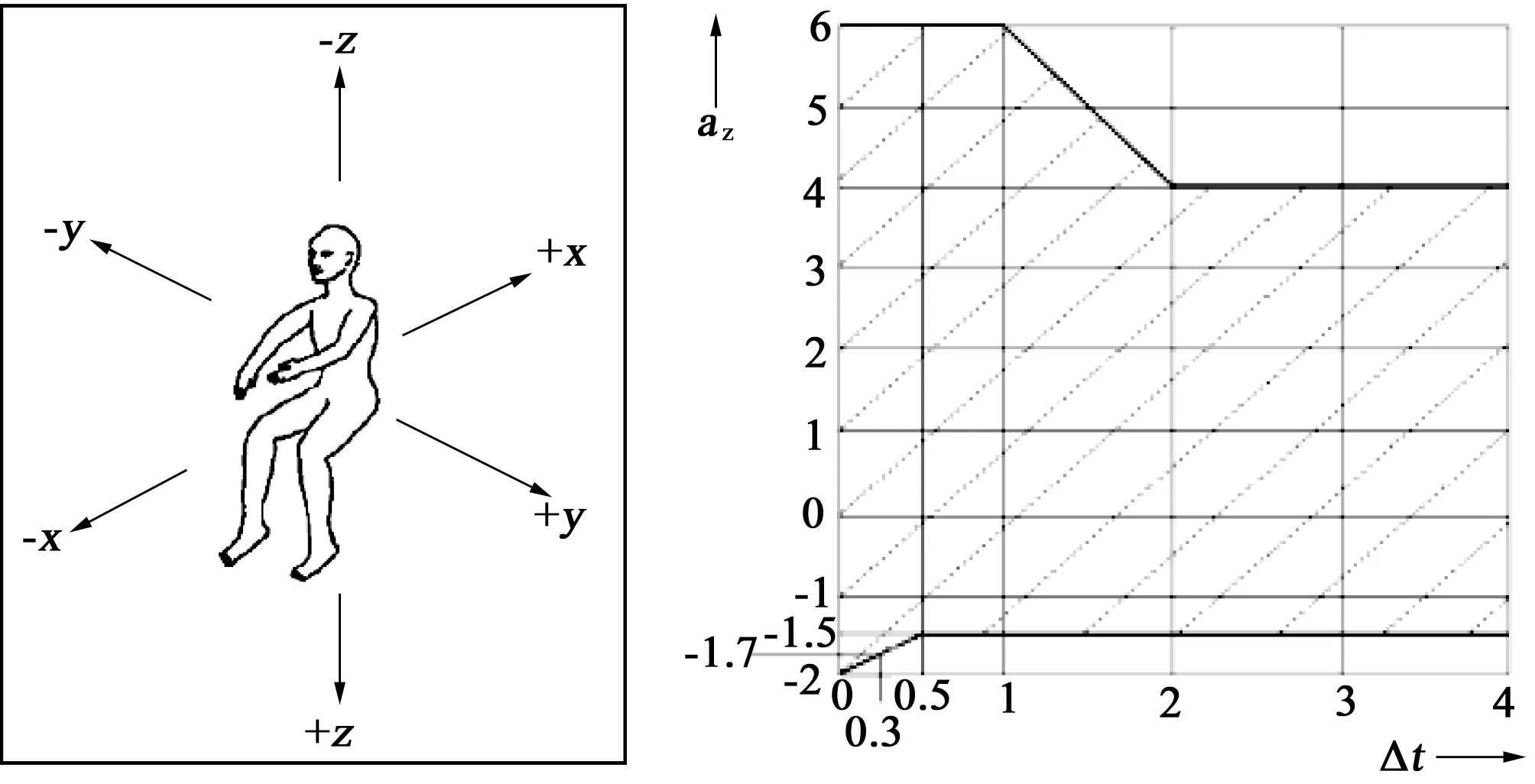
圖1 人體坐標系及允許加速度az/×g
2 理論分析
2.1 能量守恒理論分析
按照高空蹦極的運動特點,可將高空蹦極整個過程分為6個階段,如圖2所示。
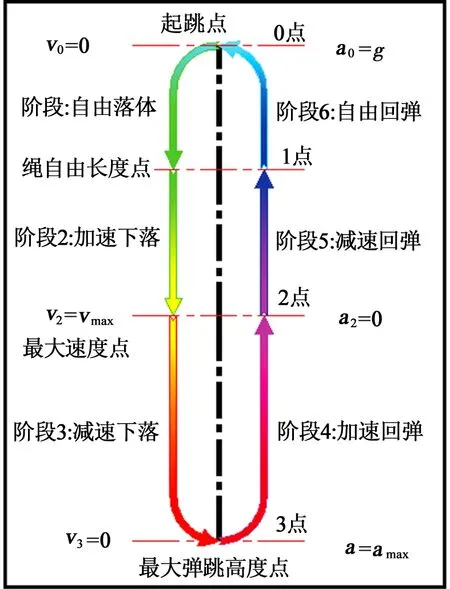
圖2 高空蹦極過程
按照能量守恒理論,系統的勢能、動能和彈性繩的彈性能以及克服空氣阻力所做的功四者能量守恒,即:
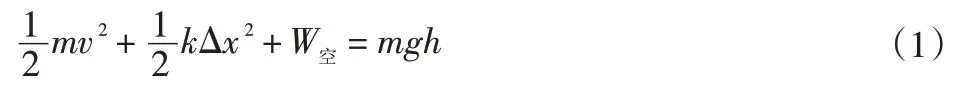
選取圖2中最大彈跳高度點(3點)進行分析,此時彈跳高度最大,彈跳者速度為0,-Z 向加速度值最大。最大加速度推導如下:

式中:K為彈性繩勁度系數,N/m;Hmax為最大彈跳高度,m;Δx 為彈性繩伸長量,Δx =Hmax-L,m;L 為彈性繩原始長度,m;g為重力加速度,m/s2;m為質點質量,kg。
設彈性繩的伸長率為1∶n,則:

由上述推導公式可知,加速度最大值與質點質量、繩長無關,僅與彈性繩的伸長率成函數關系,即在伸長率一定的情況下,最大加速度為定值。
按照GB/T 31257-2014《蹦極通用技術條件》[7]中6.3.1 可知:高空蹦極的彈性繩在彈跳者設計載荷范圍下,其最小伸長量應不小于無載長度的2.5倍,最大伸長量應不超過無載長度的4 倍。即:2.5≤n≤4(這里按照彈性繩K 值為常量,不隨伸長率變化的前提下進行n的取值),因此可得對應的加速度值如表1所示。
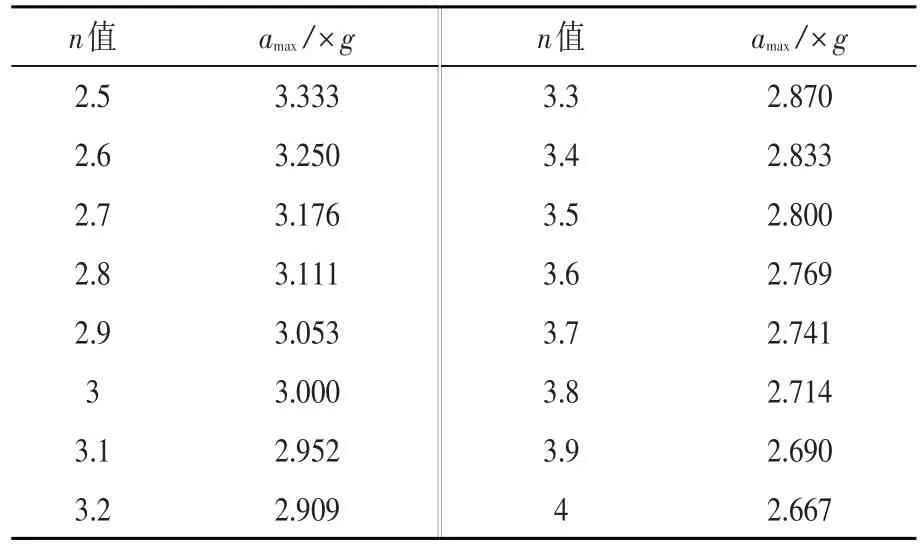
表1 彈性繩的伸長率n與最大加速度的關系
由表可知,在滿足GB/T 31257-2014 條款要求的情況下,高空蹦極Z 向加速度范圍為2.677g~3.333g。n 越大、amax越小,如果不考慮n的取值范圍,即彈性繩可以無限伸長(K值無限小),n無限增大,則:
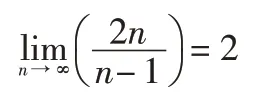
所以,在n 無限增大時,amax得到最小值2.0g,而此種情況僅為理論分析,實際是不存在的。原因如下:
(1)不存在K值無限小且能保證強度要求的彈性繩;
(2)在無限拉伸過程中,落體的最大速度也在無限增大,而受空氣阻力作用,落體在達到一定速度后,速度將不再增加;
由以上分析可知,綁腿式高空蹦極最大-Z向加速度超過圖1中允許極限加速度大小,不滿足GB8408要求。
2.2 ADAMS仿真分析
美國MDI公司研發的ADAMS軟件,是世界上使用范圍較廣的機械系統動力學分析軟件。使用ADAMS軟件,可以自動生成包括機—電—液一體化在內的、復雜系統的多體動力學數字化虛擬樣機模型,能為用戶提供從產品概念設計、方案論證、詳細設計到產品方案修改、優化、試驗規劃甚至故障診斷各階段、全方位、高精度的仿真計算分析結果,從而縮短產品開發周期、降低開發成本、提高產品質量及競爭力。由于ADAMS具有通用、精確的仿真功能,方便、友好的用戶界面和強大的圖形動畫顯示能力,所以該軟件在全世界主要企業中得到成功應用[8]。
為了進一步驗證能量守恒理論計算結果的準確性,分別以紅繩承載90 kg/65 kg 和藍繩承載65 kg/40 kg 為研究對象,采用ADAMS軟件進行動力學仿真計算,得到加速度曲線,并與能量守恒法計算結果進行比較。
本文對彈性繩的剛度通過計算進行了設定,在生產采購中應嚴格控制彈性繩的K值,并需進行試驗獲取實際K值,與設計K值進行比對,彈性繩實際的K值并非定值,而是隨伸長率變化而變化的一條曲線,因此建議在獲取試驗數據后,根據試驗所得的K值變化曲線再次進行復核。
采用ADAMS軟件進行動力學仿真計算,分別得到紅繩承載90 kg/65 kg和藍繩承載65 kg/40 kg時加速度曲線,如圖3~6所示。
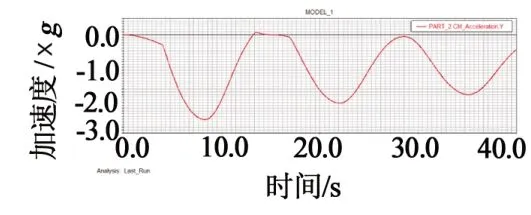
圖3 紅繩承載90 kg時加速度曲線
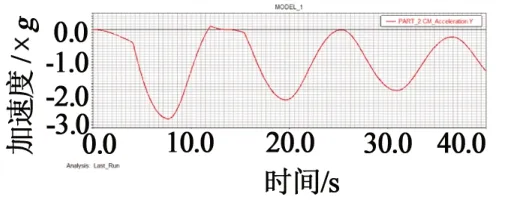
圖4 紅繩承載65 kg時加速度曲線
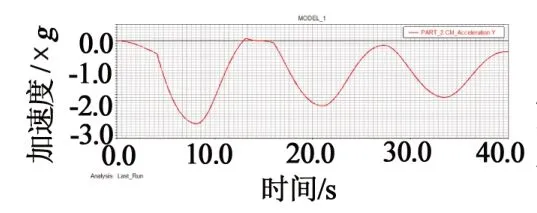
圖5 藍繩承載65 kg時加速度曲線

圖6 藍繩承載40 kg時加速度曲線
由ADAMS仿真結果可知,紅繩承載90 kg和65 kg時,-Z向最大加速度分別為2.596g 和2.731g;藍繩承載65 kg和40 kg時,-Z向最大加速度分別為2.536g和2.703g,均超過GB8408規定加速度要求。
ADAMS 仿真結果與能量守恒法計算結果比較如表2 所示。由表可以看出,ADAMS仿真結果與能量守恒理論計算結果偏差很小(小于1%),進一步證明了計算結果的可靠性。
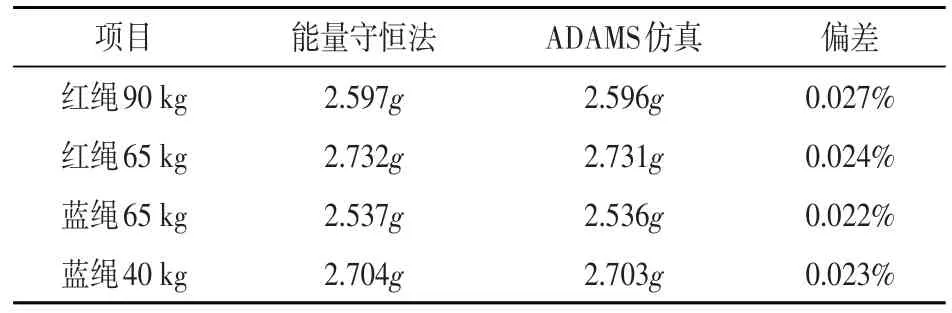
表2 ADAMS仿真結果與能量守恒法計算結果比較
3 結束語
本研究得出的主要結論如下。
(1)綁腿式高空蹦極的-Z向最大加速度與繩長、乘客質量無直接關系。
(2)綁腿式高空蹦極的-Z向最大加速度與彈性繩的伸長率有關。伸長率越大,-Z 向最大加速度越小;伸長率越小,-Z向最大加速度越大。
(3)綁腿式高空蹦極-Z 向最大加速度的理論最小值大于2.0g。
(4) 綁腿式高空蹦極的-Z 向最大加速度無法滿足GB8408-2018《大型游樂設施安全規范》中的要求。
(5)GB8408-2018《大型游樂設施安全規范》中Z向加速度的要求不適用于綁腿式高空蹦極。

