基于模糊滑模控制算法的欠驅動控制器研究*

羅文輝，張憲文，徐進釗，邱光繁，楊達明，張建民，王天雷※

（1.五邑大學智能制造學部，廣東江門 529000；2.江門市蒙德電氣股份有限公司，廣東江門 529000；3.恩平市奧達電子科技有限公司，廣東江門 529030）

0 引言

橋式吊車是一種十分常見的裝配運輸工具，由于具有負載能力強、適應性強等優點，在港口、倉庫、建筑工地等場所得到了廣泛的應用。但在實際運行過程中，其性能受負載擺動的限制，不利于工業安全和降低吊車系統的工作效率。因此，使橋吊小車能快速定位并有效地消除吊具搖擺是控制領域研究的熱點問題之一。唐超等[1]提出了一種基于線性自抗擾控制和控制器參數優化的欠驅動橋式吊車控制策略，該方法不需要對吊車模型進行任何近似解耦或線性化處理，允許模型存在一定的不確定性并且考慮了系統所受的摩檫力與空氣阻力等干擾。Ayhan 等[2]針對一種具有時變參數的橋式吊車，為了實現最小搖擺角的位置跟蹤，采用了增益調度控制方法，將載荷質量、繩長等時變參數作為調度參數，然后利用線性矩陣不等式設計了LQR 控制器。然而，這些基于線性化起重機動力學的方法可能會失去足夠的位置和負載擺動信息的準確性，從而導致一些不確定的因素降低這些起重機的控制性能。

隨著非線性控制技術的發展，許多基于橋式吊車系統的非線性控制方法被提出，如滑模控制[3-4]、最優控制[5-6]、耦合控制[7-8]、模糊控制[9-10]。其中最為典型的是滑模控制，其是一種魯棒非線性反饋控制方法，具有響應速度快、不受系統參數和外界干擾影響的特點，是解決橋式吊車控制問題的良好工具。近年來，針對欠驅動系統滑模控制器，國內外學者展開了大量的研究工作。 Lin 等[11]設計出了一種具有雙層滑模面的控制器，并且采用模糊系統來調節第二層滑模面的系數，雖然加強了系統的魯棒性，但使得整個系統的穩定性證明變得復雜。Lo 等[12]同樣也設計出了一種具有聚合式分層遞階結構的滑模控制器，但是在理論上對于該控制器的穩定性并沒有給出嚴密的證明，并且也沒有討論子滑模面上的各個系統狀態的收斂性。因此，針對基于聚合式分層遞階結構的滑模控制器，雖然已經展開了一定的研究工作，但是對于系統的穩定性分析方面都存在著難于嚴格證明的問題。

針對文獻[11-12]中存在的穩定性問題，王偉等[13]提出了一種欠驅動系統的新型滑模控制方法。該方法將系統狀態變量線性組合來引入中間變量，然后利用中間變量定義滑動面， 通過計算總的控制量保證在有限時間內，中間變量能夠收斂到平衡點，隨后進一步利用LaSalle 不變性原理證明該收斂域內只有一個平衡點且是漸近穩定的。該方法很好地解決了上述穩定性問題，但是對于抖振抑制考慮卻不太充分。

針對文獻[13]提出的新型滑模控制方法以及存在的抖振問題，本文提出了一種將滑模控制方法與模糊調節器相結合的橋式吊車防擺控制方法。通過將系統狀態分為兩組來引入中間變量，然后根據中間變量定義滑動面，利用Lyapunonv直接法推導出系統的控制率，使滑模面漸進穩定，然后針對滑模可達性與控制器增益之間的關系，設計了模糊接口系統來調節控制器增益。與傳統離散滑模控制進行仿真對比分析，仿真結果表明了該方法的可行性與有效性。

1 橋式吊車系統的非線性動力學模型

橋式吊車動力學模型如圖1所示。負載通過吊繩與臺車相連，臺車在水平力F驅動下在橋架上沿x方向運動，并受到摩檫力f的干擾，在運動過程中，臺車的運動會引起負載的擺動。

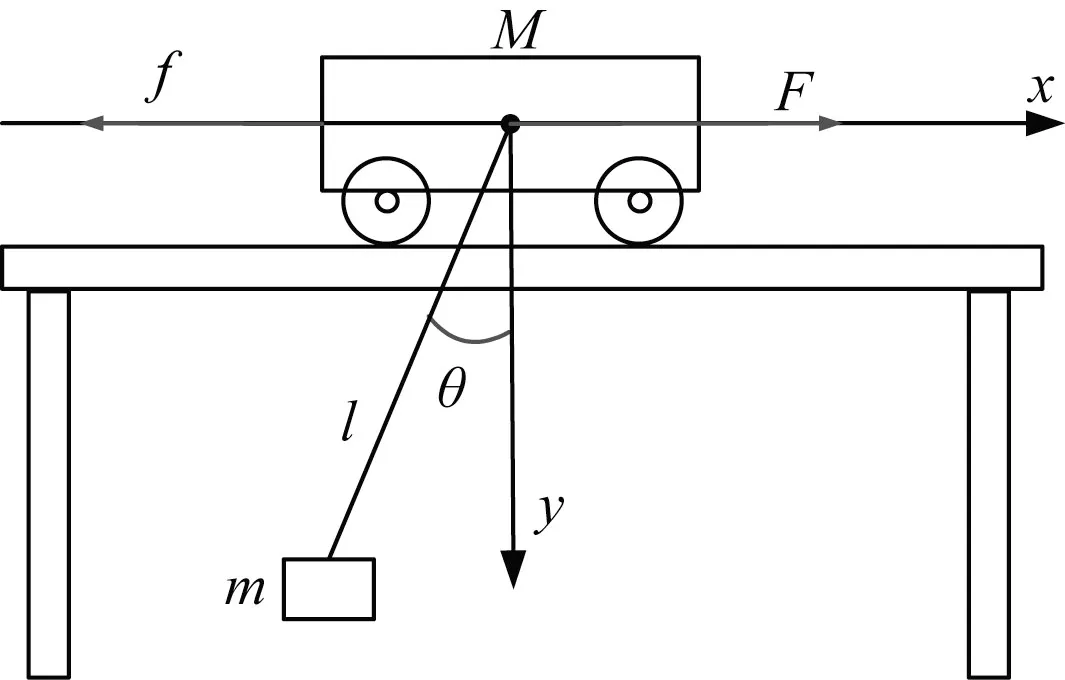
圖1 橋式吊車動力學模型

其中M為臺車質量，m為負載質量，l為吊繩長度，θ為擺動角度的大小，fr、ε、kr∈R+未知系統參數。在不失一般性前提下，做如下合理假設：（1）相對于吊物質量，吊繩的質量可以忽略不計；（2）吊繩的彈性形變忽略不計；（3）空氣阻力忽略不計。

利用拉格朗日方程得到如下橋式吊車動力學模型：

在這里g 為重力加速度，f 為臺車與軌道之間的摩檫力，采用如下模型進行描述[14]：

選擇狀態變量

狀態方程可進一步轉化為

其中， fi，bi，ci定義具體如下：

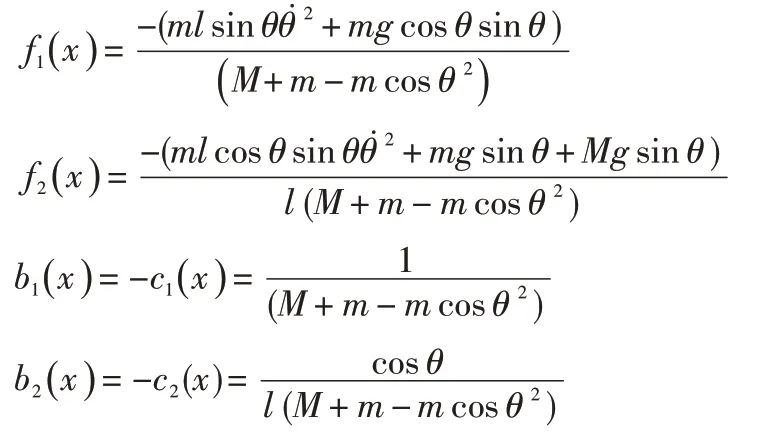
2 模糊滑模控制器設計

2.1 滑模控制器

對于橋式吊車系統，控制目標是在充分抑制并消除整個過程中負載的擺動基礎上使臺車精確、快速地到達目標位置xd處。因此，本文采用了一種將模糊調節器與滑模控制相結合的橋式吊車控制方法。首先，根據橋式吊車系統物理本質，將狀態變量分為兩組，第一組（x1x3）、第二組（x2x4），再將第一組轉化為（e1e2），其中e1=x-xd，e2=θ-θd。xd為臺車到達的目標值，θd為擺角的目標值，定義中間變量z為e1，e2兩種狀態誤差的線性組合，如式（5）所示，設置狀態位置誤差e1、擺角誤差e2，定義中間變量z為e1，e2兩種狀態誤差的線性組合：

這里，c為正數。進一步，將滑模控制的滑模面定義為：

在設計滑模控制律時，采用等效滑模控制的方法，因此，將組合滑模控制律定義為：

先不考慮摩擦力，取s˙=0 ，將（4）～（5）代入得：

為了保證滑模到達條件成立，設計切換控制如下：

2.2 模糊規則

根據系統方程式（4）可知，當干擾f 存在時，由式（9）可知，為保證系統運動在有限時間到達滑模面，增益k的值須足以消除外界干擾等不確定項的影響，才能確保滑模存在條件ss˙＜0 。因此，如果干擾f是時刻變化的，為了削弱抖振的影響，k也應該時刻變化。基于上述思想，可以設計一維模糊控制器，其根據ss˙的大小來實時地調整k 的大小。定義模糊邏輯調節增益k為：

模糊控制器的輸入變量為ss˙，輸出變量為Δk，描述輸入和輸出變量的語言值的模糊子集為：

式中：PB 為正大；PM 為正中；ZO 為 0；NM 為負中；NB 為負大。

圖2所示為模糊系統的輸入、輸出隸屬函數。

設計的模糊規則如下：

圖2 ss˙和Δk的隸屬度函數圖

2.3 穩定性分析

定理：對于式（4） 所示的橋式吊車系統，按照（5）～（6）的方式通過引入中間變量定義滑模面。最后得到的控制量如（7）所示，如果控制器參數滿足c＞0，α＞0，則各系統狀態的穩定性可得到保證。

證明：對于滑模面s采用李雅普諾夫函數：

則其導數為：

式（12）表明，所提出的控制器的輸入滿足滑模條件ss˙＜0，保證了在有限時間內各狀態量都將到達切換面s=0。

3 仿真實驗及分析

為了驗證本文提出的滑模控制與模糊調節器相結合的有效性，在Matlab Simulink環境下進行仿真實驗。圖1中橋式吊車系統參數的值分別為M=7，m=3，l=0.8，fr=4.4，erx=0.01，krx=-0.5，重力加速度g 為9.8，x 的目標值xd=2，θ的目標值θd=0。

對于橋式吊車系統，分別采用普通滑模控制、模糊滑模控制對系統的防擺定位控制進行仿真及對比分析，所設置的控制系統參數為a=1.15，c=8，η=1.3，k0=7。模糊調節器的參數分別為輸入調節因子為0.7，輸出調節因子為10。相同條件下2種滑模控制防擺定位效果如圖3所示。

圖3 兩種滑模控制防擺定位控制效果

由圖3可看出，2種滑模控制方法都實現了臺車精確、快速地到達目標位置xd處，即位移從0 m 到2 m。圖3（a）～（b）表明，模糊滑模控制對抖振抑制的效果明顯優于普通滑模控制，抖振振幅被大幅度限制，控制輸出在20 s 左右趨于0，表明了所提出的方法在減弱抖振方面的有效性。圖3（c）表明了基于模糊滑模控制器的臺車位移響應速度快于普通滑模控制，大概6 s即可到達指定位置。圖3（d）表明了普通滑模控制對抑制擺線角度效果較好，在振幅方面，兩種方法控制擺角都在1.6°之內，然而在控制響應時間方面，普通滑模控制略優于模糊滑模控制，控制響應時間約為11 s。

采用模糊滑模控制算法，吊車負載質量m從3 kg變為0.7 kg，對橋式吊車系統進行控制仿真，仿真效果圖如圖4所示。

圖4（a）表明負載質量減小時，抖振抑制效果略有加強。由圖4（b）～（c）可看出，改變負載質量m，防擺控制效差異不大，這有效地說明了本文提出的新型模糊滑模控制方法良好的魯棒性。

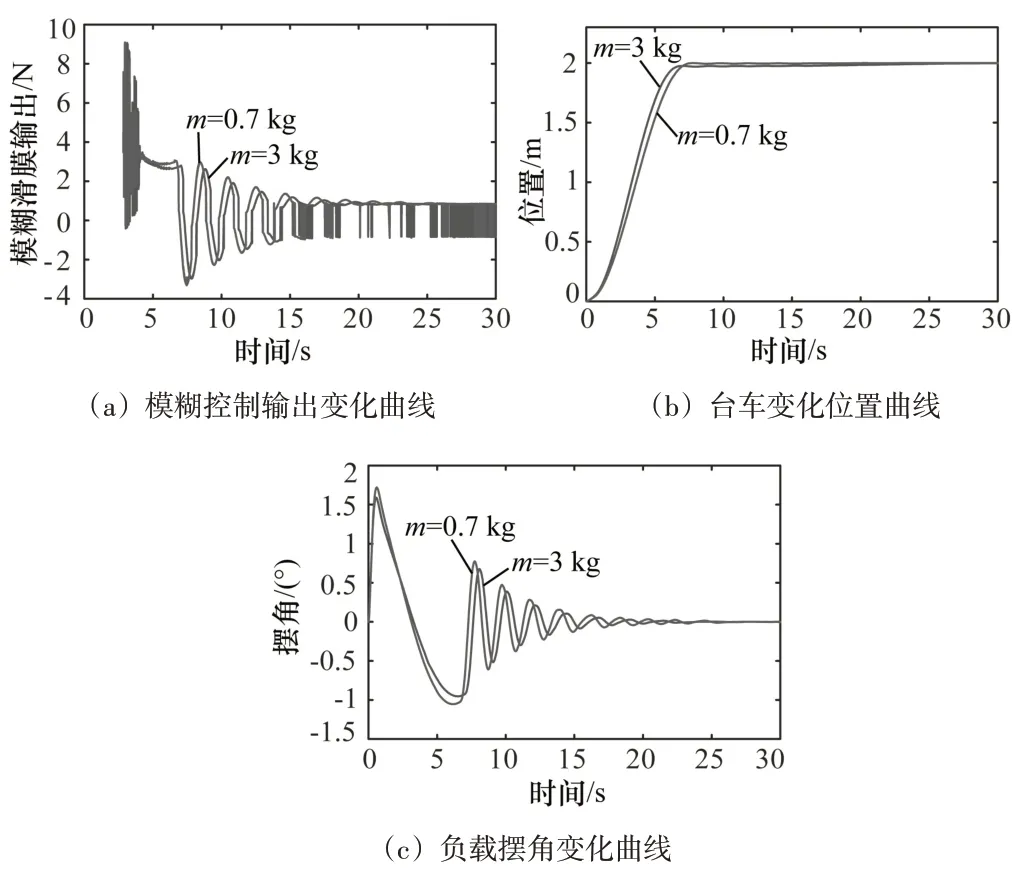
圖4 不同負載質量防擺定位控制效果

4 結束語

本文提出了一種橋式吊車系統的滑模設計方法。通過設計一個模糊接口系統調節組合滑模控制器的增益，有效降低了切換增益，解決了普通滑模的抖振問題。同時這里采用了新的滑模面，通過研究橋式吊車系統的物理特性后，引入一個中間變量，即系統狀態的一部分的線性組合，然后在中間變量的基礎上，定義了滑動面，利用李雅普諾夫方法推導了滑動面控制律。仿真實驗結果驗證了理論分析的正確性和所設計的控制器的合理性。