滿足工作流執行時限的可搶占虛擬機實例配置和調度方法研究 *

廖建錦，孫慶驍，楊海龍，欒鐘治，錢德沛

(北京航空航天大學計算機學院，北京 100191)

1 引言

科學應用中不同計算任務之間往往存在復雜的依賴關系，為了更好地刻畫不同計算任務之間的依賴關系，這些計算任務通常被組織成工作流，如CyberShake[1]和MapReduce[2]。工作流通常被表示成有向無環圖DAG(Directed Acyclic Graph)，在本文場景下，DAG和工作流可以互相替換。此外，隨著云計算市場的蓬勃發展，將工作流放置到云上計算可以更好地滿足科學應用不斷增加的計算需求。亞馬遜云服務AWS(Amazon Web Services)、阿里云等云計算服務提供商可以提供大量大小不一且可靠的虛擬機計算資源。

然而，將工作流放置到云上計算存在著幾個重要的挑戰。一方面是工作流調度的復雜性，如何將虛擬機資源映射到各個任務以滿足工作流執行時限的要求；另一方面，將工作流放到云上計算會產生大量的經濟成本，如何在滿足工作流執行時限的前提下降低成本也是個難題。其中，對于執行時限內降低工作流成本的問題，現有的研究工作提出了很多方法對工作流的虛擬機資源進行優化。例如，Abrishami等人[3]使用部分關鍵路徑解決虛擬機資源的選擇問題，但是其使用的虛擬機資源大部分是按需付費虛擬機實例[4]，這類計算資源較為可靠但價格固定，其成本優化空間相當有限。云計算服務提供商也提供了可搶占虛擬機實例[5,6]，其價格一般為按量按需付費實例的10%～20%。如果工作流虛擬機資源配置中可以利用好可搶占實例，會極大地減少工作流的計算成本。雖然可搶占實例價格低廉，但是其在執行過程中存在一定概率被云服務商收回釋放，導致工作流無法按時完成。因此，如何在工作流執行過程中，可靠地利用可搶占實例，在滿足執行時限要求的情況下，降低計算成本是一個新的挑戰。

針對上述挑戰，本文提出了滿足工作流執行時限的可搶占虛擬機實例配置和調度方法，可以在滿足工作流最長執行時限的前提下，最小化工作流執行的計算成本。本文提出的方法具有重要的實際經濟價值。具體而言，本文的主要貢獻如下所示：

(1)提出了基于馬爾科夫模型的可搶占虛擬機實例價格預測模型。

(2)提出了針對單任務的成本估計方法。通過估計不同出價策略下的工作流計算成本，從中選擇最優出價策略。

(3)提出了基于可搶占虛擬機實例價格特點的工作流配置和調度方法。

(4)基于阿里云真實數據，對本文提出的方法進行模擬驗證，并與已有算法進行對比。

2 研究背景

2.1 可搶占虛擬機實例

可搶占實例是云計算市場中較為特殊的一類資源，其價格低廉，但生命周期不再只由用戶決定，還和市場有關[5,7]。用戶需要提供出價以創建可搶占實例，而創建可搶占實例是否成功還和市場價格以及資源是否充足有關。當用戶出價大于市場價格且資源充足的情況下，用戶可以成功創建可搶占實例。其中市場價格取決于市場供需關系，隨時間發生波動。在用戶成功創建可搶占實例后，云計算服務提供商會不斷檢查用戶出價和市場價格，當市場價格大于用戶出價或資源不足，那么該用戶的可搶占實例就會被云計算服務提供商收回并釋放。由此可知，當用戶出價較高時，可搶占實例會更加穩定，但相應地價格也會更加昂貴。

可搶占實例的出價策略主要分2種：靜態出價策略和動態出價策略。靜態出價策略一般目標比較單一，常見的有依據歷史價格出價和預測未來價格出價。Andrzejak等人[8]提出了一種概率模型，其證明當出價為最低價或者平均價格時，一般規律是出價越高成本越高，但相應地完成時間會更短。Baughman等人[9]利用LSTM預測未來價格變化，而Fabra等人[10]首先對各個可用區進行分類，然后根據其不同的價格特點分別建模預測價格。總而言之，靜態出價策略比較簡單，出價的高低對應著任務對時間和可靠性的要求。

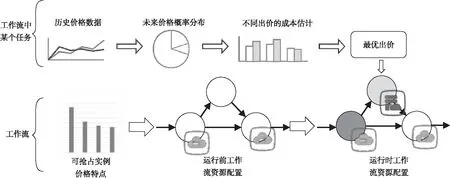
Figure 1 Spot instance configuration and scheduling method proposed in this paper圖1 本文提出的可搶占虛擬機實例配置和調度方法WCSSI

相比靜態策略，動態策略可以協同優化計算成本和完成時間。對此，許多研究提出了在不同約束條件下的出價策略，比如限制成本或者計算時間等。Kamiński等人[11]提出了一種自適應的出價策略，該策略可以同時降低計算成本和實例回收帶來的延遲。Zafer等人[12]則將此類問題建模為一般的離散時間動態規劃問題，并提出了最優出價策略，該策略可以在固定時間內最大程度地降低計算成本。相對而言，動態出價策略可以在一定約束條件下獲得比較好的結果，但是建模和求解會相對比較復雜。

2.2 工作流調度優化

眾所周知，工作流調度是一個NP-complete問題[13]。當工作流放置到云上進行計算的時候，成本是研究關注的重點問題之一。在云上進行工作流調度，比較常見的場景包括有限時間內最小化成本和有限成本內最小化執行時間。除此之外，還有研究討論云計算實例的計算能力和工作流的魯棒性問題。

對于在有限時間內最小化成本的問題，一般的方法是選擇較為廉價的資源分配給非關鍵路徑上的任務，如此便可以在不增加工作流整體運行時間的基礎上降低成本，其中比較常見的方式是通過時間分配來選擇資源。例如，Yu等人[14]根據工作流中的依賴關系對各個任務進行分類，然后根據每個任務的類別來分配時間，最后按照分配的時間來為任務選擇不同的資源。除此之外，也有研究利用關鍵路徑來選擇資源。例如，Gao等人[15]利用關鍵路徑和最短路徑對工作流中的各個任務進行分類，然后按照一定的優先級來逐步減少各個任務的計算成本，從而降低整個工作流的成本。Abrishami等人[3]則是利用部分關鍵路徑并通過遞歸的方式來決定各個任務的資源分配。

鑒于可搶占實例比較廉價，部分學者在工作流中加入可搶占實例以降低工作流成本。Monge等人[16]提出了CMI(Cloud Multi-objective Intelligence)，其同時考慮了工作流的時間和出錯概率，通過遺傳算法求解。Poola等人[17]則是通過啟發式算法來使用搶占式實例，進而降低工作流的成本。Zhou等人[18]用A star算法進行剪枝，然后調整各個任務的資源分配，從而以一定的概率使工作流不會超時。這些算法對于搶占式實例的出價大都以盡可能保證能夠獲得可搶占實例為主，并沒有考慮進一步降低有限時間內獲得可搶占實例的成本。另外，由于期限的不同，可搶占實例的期望價格也不一樣，當工作流執行時限過大時會出現邊際效應，會帶來虛擬機利用率的問題。此外，不同可搶占實例的價格差異很大，這些差異很大程度上影響工作流整體的配置。上述算法如果能考慮到這些問題，那么可以進一步降低工作流的成本。

3 WCSSI方法設計實現

3.1 總體設計

本文提出的可搶占虛擬機實例配置和調度方法WCSSI(Workflow Cost Saver based on Spot Instance)的整體結構如圖 1所示，具體包括價格預測、成本估計和工作流配置和調度3個部分。首先根據可搶占實例的價格特點，在工作流執行前通過工作流配置算法確定工作流中任務所選擇的可搶占實例，在工作流配置的層次上降低計算成本。之后在工作流執行過程中，根據工作流的執行情況調整任務的執行時限和使用的可搶占實例資源。最后，在為任務購買可搶占實例時，通過成本估計和價格預測成本最低的方式，在單任務的層次上降低計算成本。

接下來對本文方法進行建模，首先做出如下假設：

(1)市場的可搶占實例資源充足，在購買可搶占實例時，只要用戶出價大于或等于市場價格即可獲得可搶占實例。

(2)可搶占實例只有可能在任務結束時或者市場價格大于用戶出價時才會被釋放。當可搶占實例被服務提供商釋放時，會產生一定的成本，該成本為實例從最近檢查點到被釋放時產生的計算成本。

(3)可搶占實例的價格每小時變化一次，而且其收費也是按照小時收費。

(4)決策只針對單個任務，不會影響可搶占實例市場的價格變化。

(5)每小時執行一次檢查點，并忽略進行檢查的時間和從檢查恢復的時間。

(6)忽略可搶占實例的性能變化，以及傳輸所需要的時間。

3.2 工作流配置和調度

一般來說，工作流調度的原則是讓工作流盡可能使用價格低廉的資源。對于按需付費實例，其3xlarge、2xlarge、xlarge的關鍵指標，如CPU數量、內存大小，分別為large的6,4,2倍，而價格也是如此，所以單位計算資源的價格相同。但是，對于可搶占實例這類價格一直在變化的資源，很難直接判斷資源的使用優先級。所以，本文根據可搶占實例的歷史平均價格，對可搶占實例進行排序。

圖 2是可用區(可用區是指云計算提供商的物理數據中心內，電力和網絡相互獨立的物理區域)cn-beijing-h的不同規格可搶占實例的平均價格相對于按需付費實例的價格。可以發現，其中3xlarge的價格最高，然后2xlarge、xlarge、large的逐漸降低，但降低幅度也越來越小。為了降低工作流的計算費用，整個工作流應該盡可能使用較低規格的實例。同時，還需要考慮各個規格之間的差價，工作流中各個任務的規格不能相差太大。除此之外，還需要考慮到各個任務對工作流執行時長的影響。在這里本文提出了BFRC(Branch First Reduce Cost)工作流資源調度算法。

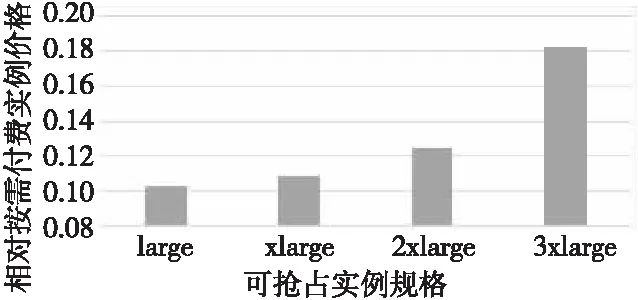
Figure 2 Relative price of spot instances(compared with the price of on-demand instances of the same specifications)圖2 可搶占實例的相對價格(與同規格的按需付費實例價格相比)

根據上述可搶占實例價格特點，首先進行工作流的配置和調度。配置算法如算法1所示：

算法1工作流資源調度(BFRC)

輸入：工作流、工作流執行時限、可供選擇的資源、可搶占實例的歷史價格數據。

輸出：工作流的資源調度。

步驟1工作流的全部任務選擇最貴的資源(即算力最強)，計算整體工作流的執行時間；

步驟2對工作流的各個任務進行分類；

步驟3根據工作流執行時限和工作流的執行時間，分配各個任務的執行時限；

步驟4根據任務的執行時限，為各個任務選擇合適的可搶占實例；

步驟5按照特定優先級，調整各個任務的資源使用。

步驟1是在工作流執行前的初始化配置，主要是為了得到整體工作流的執行時間，由此確定工作流是否能在執行時限內完成。

步驟2是對工作流中的任務進行分類，如圖 3所示，這里借鑒了Yu等人[14]的分類方法，將任務分為簡單任務和同步任務2類：前驅或者后繼不止一個的任務分類為同步任務，其它任務為簡單任務。同步任務在工作流執行的過程中起到了對其他任務的同步作用，這類任務對于工作流的影響比其他任務更明顯。然后對簡單任務進行篩選，如果簡單任務為某同步任務的唯一后繼或者唯一前驅，那么調整該簡單任務所產生的影響和調整其相鄰的同步任務所產生的影響類似，所以該簡單任務也應該歸屬于同步任務。

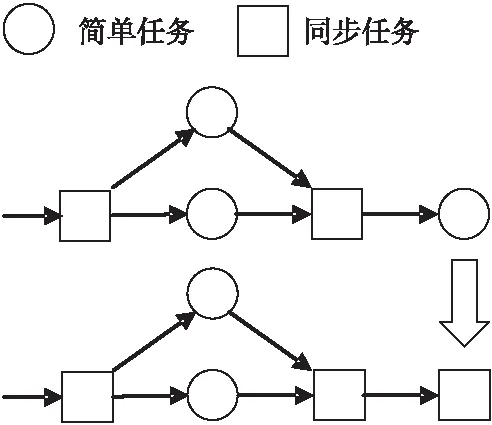
Figure 3 Classification of workflow task圖3 工作流任務分類

步驟3和步驟4是按照各個任務的工作量，分配相應的執行時間，這樣使得每個任務的執行時間和選擇的資源盡可能平均。

步驟5是為了利用工作流中剩余空閑時間，從而進一步降低各個任務的規格。如圖 4中的任務A、B分別有1.7 h和1.6 h的執行時限,各自的計算時間為1.0 h，如果將時間碎片合并利用，A的計算成本可以進一步降低。除此之外，不同類型的任務對工作流計算的影響程度也不同，對此我們更傾向于優先降低簡單任務的節點規格，如圖 3所示，可以同時降低相同起點和終點的多個簡單任務的計算成本。

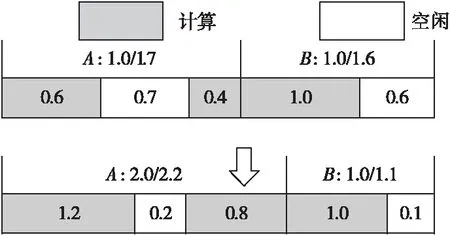
Figure 4 Using time fragments in the workflow圖4 利用工作流中的時間碎片

當完成工作流執行前的資源配置之后，需要考慮如何在工作流執行時使用可搶占實例，即設置任務的執行時限來減少計算成本。首先要保證每個任務的執行時限不會導致工作流超時，即每個任務都不能晚于最晚完成時間完成計算。其次圖 5表示理想狀態下，每種可搶占實例在不同執行時限的情況下的最低價格。從圖5中可以發現，價格和執行時限有著非常大的關系，除了large和xlarge這2種可搶占實例的價格范圍相近，其他類型之間的價格范圍差距很大。考慮到這是理想情況下的結果，實際上各種出價策略下各個可搶占實例的價格變化可能會更小。因此，對于每個任務增加執行時限的比例不如降低規格所帶來的成本降低更大。在這種情況下，每個任務的執行時限不應該過大，例如當任務的執行時限和計算時間的比例超過1.5倍時，反而有可能會出現如圖4所示的時間碎片過多的情況。或者在任務的執行時限比較大的情況下將計算資源調整為更加廉價的可搶占實例。綜上，對于每個任務的執行時限有2個上限，只需要選擇其中比較小的作為任務的執行時限即可。

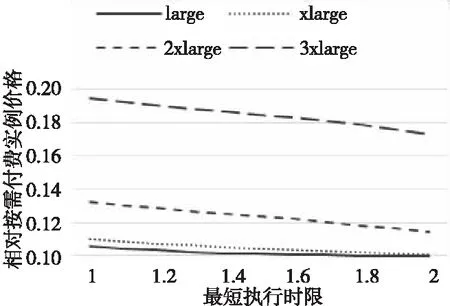
Figure 5 Spot instance relative minimum price圖5 可搶占實例最低相對價格

3.3 成本估計方法

確定任務所選擇的可搶占實例類型之后，還需要考慮如何降低可搶占實例的購買成本，從而在工作流執行時限內降低計算成本。這樣問題就變為單任務的可搶占實例購買問題，本文給出了不同出價的成本估計方法，通過估計不同出價的成本可以得到成本最低的最優出價。

首先假設該計算任務一共需要ch完成，執行時限為th，假設代價函數為cost，那么根據可搶占實例的特點可以設置一些邊界條件。

首先要保證該任務不能超時，還要考慮到可搶占實例可能會由于市場資源緊張而出現購買失敗或者被釋放的情況，所以在c=t時，必須使用按需付費實例來進行計算，此時cost=priceod*c，其中priceod是按需付費實例的價格。

s代表可搶占實例的市場價格，則s∈(0,priceod]。當c=t-1時，為了避免使用按需付費實例，用戶出價應為priceod。根據上文的假設，可搶占實例一定會購買成功，且不會被釋放，可以得到：

(1)

其中si代表ih后可搶占實例的市場價格。

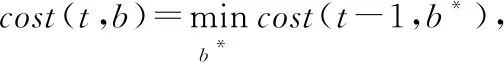
cost(t,b)=g(b)*E(s)+(1-g(b))*

(2)

其中s≤b，如此可以將一個問題進行遞歸求解。當c≥2時，還需要考慮剩余的任務要如何處理，所以相比于c=1的情況，在成功購買時，這里又多了一項cost(c-1,t-1,b)，其中c代表所需要的計算時間，t代表執行時限，b代表用戶出價。因此，計算成本可以表示為:

cost(c,t,b)=g(b)*

E(s+cost(c-1,t-1,b))+(1-g(b))*

(3)

3.4 價格預測模型

在得到了估計不同出價時計算成本的遞歸求解公式之后，接下來的問題就是如何得到其中的g(b)和E(s)等函數。這些函數很明顯和可搶占實例的價格有著很大的關系，如果可以預測可搶占實例的未來價格，便可從中得到這些函數的計算結果。

這里使用馬爾科夫模型來預測可搶占實例的價格變化。首先根據已有的歷史價格數據得到概率轉移矩陣P，其中pss′代表可搶占實例價格從s變為s′的概率，然后通過該矩陣來預測未來價格。由于未來價格還和當前價格有關，所以cost、g(b)等函數需要增加參數進行計算，其代表當前可搶占實例的價格。可以得到：

(4)

(5)

將式(4)和式(5)代入式(3)中化簡得到：

cost(c,t,b,s)=

(6)

如果增加實例被釋放或者購買失敗的成本，則式(6)可以寫為:

cost(c,t,b,s)=

(7)

其中，r是可搶占實例回收產生的成本。

如此便得到了計算不同出價的成本估計函數，用戶出價b為成本估計的最小值：

(8)

4 實驗評估

4.1 實驗設置

工作流：本文使用由Pegasus[19]提供的具有代表性的工作流來進行測試，包括CyberShake、Sipht、Inspiral和Epigenomics。

資源設置：使用阿里云的不同可用區的數據，包括cn-beijing-h(北京地區h可用區)、cn-shanghai-f(上海地區f可用區)和cn-shenzhen-e(深圳地區e可用區)。本文使用g6系列的實例進行測試。此外，歷史價格為可搶占實例在2019年10月10日到2019年12月19日的價格。這些歷史價格的數據特征如表1～表3所示。

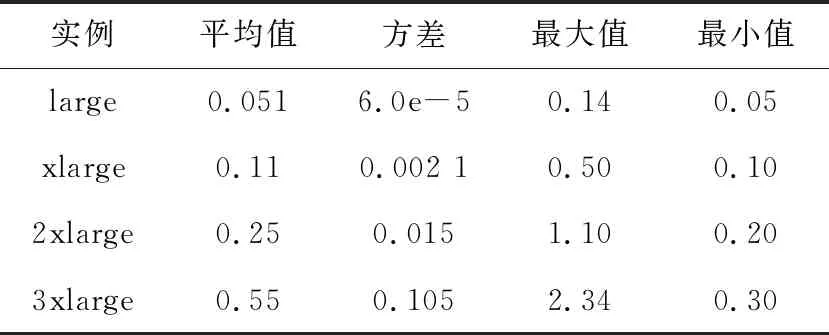
Table 1 Available zone cn-beijing-h g6 family price characteristics

對比算法：本文選取Poola等人[17]提出的AIB(Aggressive with Intelligent Bidding)算法作為對比，該工作也是利用可搶占實例來降低工作流

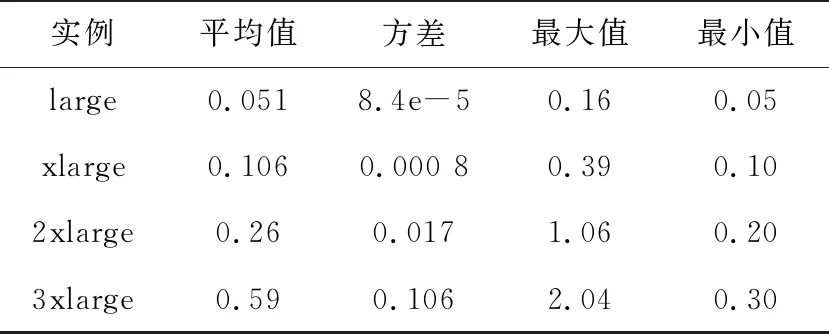
Table 2 Available zone cn-shanghai-f g6 family price characteristics

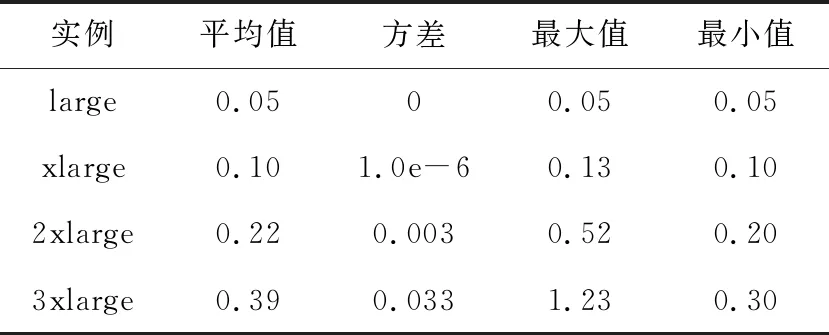
Table 3 Available zone cn-shenzhen-e g6 family price characteristics

的計算成本。基準實驗為全部都用按需付費實例執行工作流。在實驗驗證中，每組實驗進行30次取平均值，每次都隨機選擇開始時間。每次測試的工作流執行時限大小從工作流執行時間的1.1倍開始，然后逐漸遞增到3.0倍。

最低成本下限：為了更好地理解不同算法對工作流計算成本的節省效果，這里定義了最低成本下限。為了簡化計算，假設工作流從開始到結束只有一條路徑，那么其配置最多有2種可搶占實例，例如只有3xlarge和2xlarge，所以其配置比例變化可以近似為如下不等式：

(9)

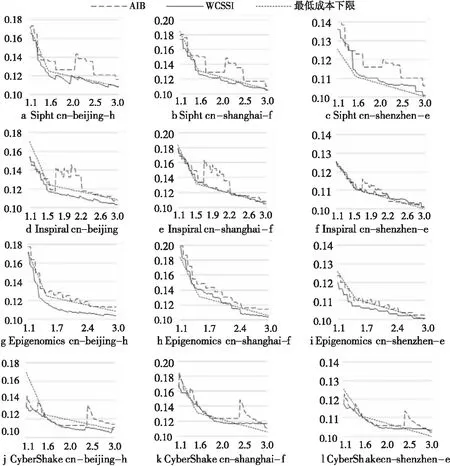
Figure 6 Relative cost of WCSSI and AIB, the benchmark is the cost of all on-demand instances圖6 WCSSI與AIB的相對成本，基準為全部使用按需付費實例的成本

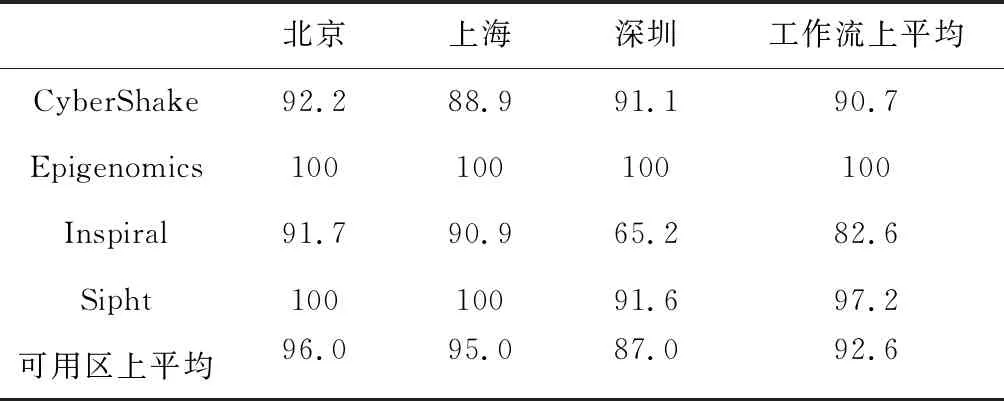
其中，w為計算任務大小，d為最長計算時間(deadline)，t1、t2分別是2種可搶占實例的執行時間，c1、c2分別是2種可搶占實例每小時能夠完成計算任務的大小，p1、p2分別是2種可搶占實例每小時的價格，不妨假設c1>c2，根據圖 5所展示的關系，有1

(10)

4.2 實驗結果與分析

實驗結果如圖 6所示，其中WCSSI的成本比AIB的成本更低。在圖 6中，WCSSI的成本是基線成本的 10.1%～19.8%(最高可節省89.9%)，平均為11.7%；相對于AIB為76.8%～104.2%(最高可節省23.2%)，平均為94.2%。這得益于對于任務的分類處理，通過優先對簡單任務調整可搶占實例類型，使得更多簡單任務也因此受益，從而使得工作流使用更多價格較低的可搶占實例，進一步降低工作流的計算成本。而AIB則是為先執行的任務分配廉價資源，再對后執行的任務分配。這樣的結果是先執行的任務可搶占實例價格很低，但是執行時間特別長，而后執行的任務只能使用較為昂貴的資源，從而增大了工作流的計算成本，這也是在某個區間內工作流執行時限越大成本反而上升的原因之一。對于結構復雜的工作流，例如CyberShake，簡單任務節點很少，甚至沒有簡單任務節點。這種情況下WCSSI的性能和AIB的性能類似，但是受益于資源平均分配的策略，WCSSI能夠有效避免出現反常成本上升問題。

表4是WCSSI表現優于AIB的比例，在大部分工作流和可用區價格數據下都達到了90%以上(在Inspiral工作流與cn-shenzhen-e價格數據上，WCSSI優于AIB比例最低，為65.2%)。在WCSSI成本高于AIB的情況下，成本高出的平均比例為1.1%，差距并不明顯。在其它WCSSI優于AIB的情況下，成本比例為89.7%～98.2%，平均為93.5%。在所有工作流和可用區價格數據組合下，當WCSSI成本高于AIB時，成本高出比例為0.5%～1.9%，平均為1.0%。

Table 4 WCSSI outperforms AIB experiment ratio

除此之外，WCSSI的成本最終收斂到基線成本的10%，結合圖 5所示的平均價格，這可能代表計算成本優化已經接近上限，接下來將對此進行分析。

從圖 6e和圖6f可以發現，WCSSI的折線軌跡基本和最低成本下限一致。考慮到工作流Inspiral 中非簡單任務的比重極少，且各個分支比重相當，可以近似為多個假設的工作流混合而成，所以認為WCSSI已經達到了最低成本下限。

而圖 6g和圖 6i中WCSSI成本低于最低成本下限，這是因為Epigenomics不符合且不可近似為上述假設的工作流，簡單任務和非簡單任務在工作流中都有著很大的比重。由于WCSSI優先降低簡單任務的成本，所以低成本可搶占實例在工作流中所占的比重會比估計的要高，從而使得WCSSI的運行成本低于最低成本下限。

綜上，WCSSI得出的工作流計算成本可以達到最低成本下限。

5 相關工作

云計算中可搶占實例的出現，為降低工作流執行成本提供了巨大優化空間，Poola等人[17]通過結合使用可搶占實例和按需付費實例，以在滿足執行時限的要求下降低工作流的計算成本。其使用激進算法和保守算法來估計工作流中各個任務的執行時間，然后使用計算得到的最晚執行時限(按需付費下)來決定工作流在執行的過程中是否可以使用可搶占實例來降低成本。WCSSI相比于該算法，考慮了不同任務對于工作流執行時限的不同影響，通過對任務進行差異化處理可以更好地節省工作流計算成本。在購買可搶占實例的策略上，Zafer等人[12]將其建模為動態規劃問題來得到最優出價策略，但是其沒有考慮實例被釋放所帶來的成本，且價格模型比較簡單。本文提出的成本估計方法則考慮了實例釋放所帶來的成本，且使用馬爾科夫模型，更加貼近實際情況。

6 結束語

本文提出了滿足工作流執行時限的可搶占虛擬機實例配置和調度方法，可以極大地降低工作流的計算成本。本文選取了有代表性的工作流負載，并在阿里云真實數據上進行了實驗驗證。實驗結果顯示，本文提出的工作流調度方法可以最高節省89.9%的成本開銷。在未來的工作中，我們會考慮可搶占實例的性能變化因素，并在工作流配置和調度中考慮其對執行時限的影響。