四旋翼飛行器的自抗擾控制研究

李定聰 龐中秋

摘 要 本文將根據四旋翼飛行器的動力學模型和數學模型，設計自抗擾控制器，并利用MATLAB-Simulink模塊搭建其控制器，對其系統進行解耦控制，優化整定控制器參數。仿真實驗實現對其高度和姿態的穩定控制，對其的穩定性、抗擾性、魯棒性進行分析。

關鍵詞 四旋翼飛行器;自抗擾控制技術;Simulink

Abstract In this paper， the auto-disturbance Rejection Controller （ADRC） is designed according to the dynamic model and mathematical model of four-rotor aircraft， and the controller is built with MATLAB-Simulink module to decouple the system. Optimal Tuning of controller parameters. The simulation experiment realizes the stability control of its altitude and attitude， and analyzes its stability， anti-disturbance and robustness.

Key words Quadcopter; Active Disturbance Rejection Control; Simulink

引言

進入21世紀，由于微電子系統和飛行控制、能源動力等技術研究的成熟，旋翼飛行器的自動控制器順勢而生，為控制技術的發展帶來了前所未有的機遇，許多的學者專家加入到對旋翼飛行器的研究和探索之中，因此飛行器的性能和結構也逐漸得到了優化。目前，四旋翼飛行器主要應用于軍事和民用領域，在民用領域能夠代替人類去完成某些任務， 在軍事領域上由于其結構簡易，機動性較為靈活，在裝備了具有殺傷性武器后有很強的戰斗能力。所以在國內外都有許多研究機構對于四旋翼飛行器都進行了深入的研究。

1概述

控制的核心和本質是構建一個相當精確的系統模型，基于閉環的結構，在理想的環境中，找到使其穩定的方式。從實際應用的觀點出發，控制的核心應該是找到抗擾機制，對過程或系統中存在的干擾與不確定性進行抑制。盡管PID控制技術應用范圍廣泛，控制效果較好，然而隨著控制系統越來越復雜，PID的局限性越發明顯，其魯棒性較差，容易出現飽和。各種改進的PID算法也不同程度地遇到了瓶頸。在實際的生產過程中，存在的擾動通常不止一種或幾種，而且控制對象的精確模型難以獲得。在這樣復雜的條件下，實現對系統的穩定控制，實現對擾動的抑制，需要尋求更優秀的控制方法。

基于這樣的認識，自20世紀80年代末開始，我國韓京清研究員相繼開發出非線性跟蹤微分器，擴張狀態觀測器等對信號處理及控制具有獨特功能和效率的新型非線性結構，從而開發出一系列新型非線性實用控制器。其中，自抗擾控制器（ADRC）最具代表性，因而統稱為“自抗擾控制技術”。自抗擾控制技術是深入認識經典調節理論與現代控制理論各自優缺點，大量運用計算機仿真實驗探索和改進而發展出來的。

1.1 自抗擾控制器的組成

經典自抗擾控制器由TD跟蹤微分器（Tracking Differentiator），NLSEF非線性狀態誤差反饋控制律（Nonlinear State Error Feedback），ESO擴展狀態觀測器（Extended State Observer）三個部分組成。

1.2 安排過渡過程與跟蹤微分器（TD）

事先安排過渡可以使誤差反饋增益和誤差微分反饋增益的選取范圍擴大，從而使其整定更容易;可以讓給定的反饋增益所能適應的對象參數范圍擴大，讓控制器的魯棒性更好。

直接以e=v-y的方式產生原始誤差并不合理。然而PID控制的優點是基于誤差反饋來消除誤差。初始時刻y=0，產生的誤差很大，尤其容易讓系統產生超調。安排過渡過程可以有效解決超調和快速性矛盾。

安排過渡過程使誤差反饋增益和誤差微分反饋增益的選取范圍擴大，從而參數整定更為方便。它們能適應對象參數范圍擴大，即控制器的魯棒性更強。

1.3 非線性誤差反饋控制率

引入控制作用的動力學系統成為受控系統。反饋機制是經典動力學系統中沒有，而系統固有的機制，反饋機制的引入能使系統的性能在很大程度上到達人們理想的狀態。反饋的機制能讓線性系統變為非線性系統，反之很多情況下也能使非線性系統成為線性受控系統。這就使得非線性和線性之間的關系變得模糊。被控系統中的反饋機制，擁有抑制擾動的能力。但是不同形式的反饋抑制擾動的能力有很大差異。

由于TD微分器和安排過渡過程的運用，能夠產生過渡過程的誤差信號。利用該誤差信號 和誤差微分信號，可以生成誤差積分信號，進而實現PID控制。但是這種PID組合并不好。然而非線性組合的效果更好。而由于擾動能夠得到估計和補償，所以誤差積分信號可以不用。原系統就可以化為線性積分器串聯型系統，設計可以用一般的誤差反饋來實現，讓閉環系統得到理想的性能。

1.4 擴展狀態觀測器

系統在運行過程中一直在與環境進行信息交流，系統把某些部分狀態變量信息傳給外部，從系統外部得到某些信息，就是外部和系統是信息交換的過程中發展。人們只能收集系統外部變量來把握系統的運行狀態。根據測量到的系統輸入（控制量）。狀態觀測器就是系統的輸出可以確定系統內部狀態信息的裝置。

擴展狀態觀測器的基本思想：把總擾動擴張成為一個新的狀態變量，然后利用系統的輸入，輸出重構出包含系統原有的狀態變量與擾動的所有狀態[1]。

2四旋翼飛行器的自抗擾控制研究

對四旋翼飛行器自抗擾控制器（ADRC）進行建模，其中包括跟蹤微分器、非線性誤差反饋控制律、三階擴展狀態觀測器。因為四旋翼飛行器是一個欠驅動、強耦合、非線性的動力學系統。所以在姿態控制通道、俯仰通道、橫滾通道、偏航通道，它們相互耦合。所以對通道解耦在設計控制器時是一個不可忽視的問題，下文將對其系統進行解耦，最后對控制器進行matlab仿真實驗，分析各通道自抗擾控制器的控制性能。

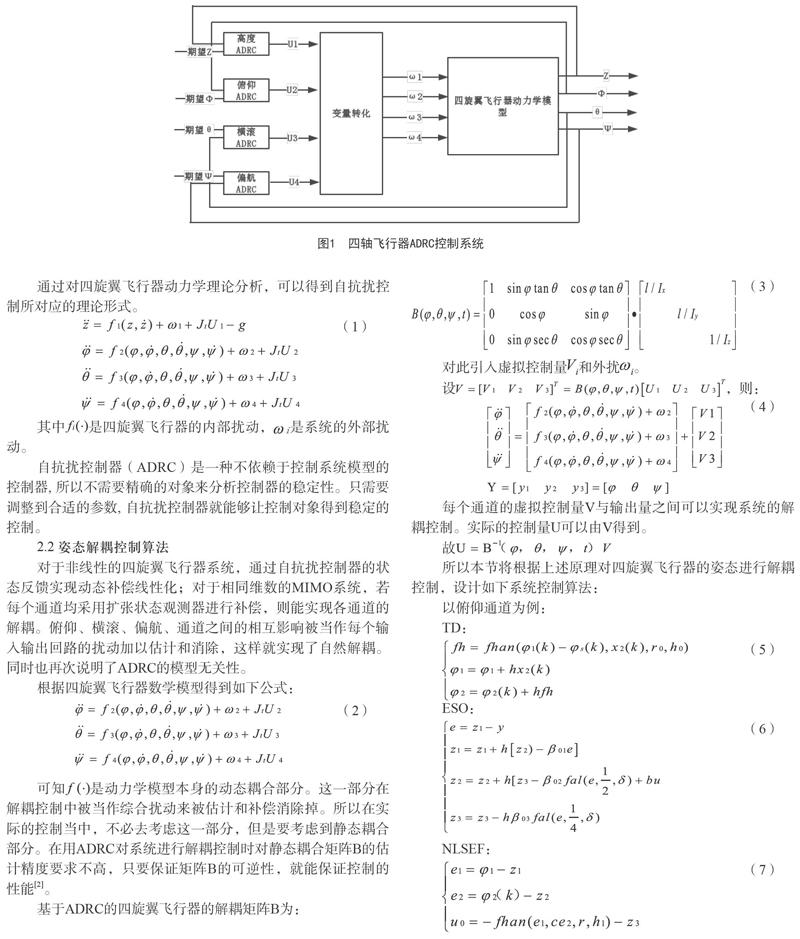
2.1 四軸飛行器ADRC控制系統設計

基于ADRC控制的四旋翼飛行器系統設計方案如下圖， 分為4個獨立的回路：高度控制通道、俯仰控制通道、橫滾控制通道和偏航控制通道，將自抗擾控制器（ADRC）分別針對每個通道進行設計。

通過對四旋翼飛行器動力學理論分析，可以得到自抗擾控制所對應的理論形式。

其中是四旋翼飛行器的內部擾動，是系統的外部擾動。

自抗擾控制器（ADRC）是一種不依賴于控制系統模型的控制器， 所以不需要精確的對象來分析控制器的穩定性。只需要調整到合適的參數， 自抗擾控制器就能夠讓控制對象得到穩定的控制。

2.2 姿態解耦控制算法

對于非線性的四旋翼飛行器系統，通過自抗擾控制器的狀態反饋實現動態補償線性化;對于相同維數的MIMO系統，若每個通道均采用擴張狀態觀測器進行補償，則能實現各通道的解耦。俯仰、橫滾、偏航、通道之間的相互影響被當作每個輸入輸出回路的擾動加以估計和消除，這樣就實現了自然解耦。同時也再次說明了ADRC的模型無關性。

根據四旋翼飛行器數學模型得到如下公式：

可知是動力學模型本身的動態耦合部分。這一部分在解耦控制中被當作綜合擾動來被估計和補償消除掉。所以在實際的控制當中，不必去考慮這一部分，但是要考慮到靜態耦合部分。在用ADRC對系統進行解耦控制時對靜態耦合矩陣B的估計精度要求不高，只要保證矩陣B的可逆性，就能保證控制的性能[2]。

基于ADRC的四旋翼飛行器的解耦矩陣B為：

對此引入虛擬控制量和外擾。

每個通道的虛擬控制量V與輸出量之間可以實現系統的解耦控制。實際的控制量U可以由V得到。

2.3 控制器參數整定

自抗擾控制器的跟蹤微分器、非線性反饋控制律、擴展狀態觀測器三個重要的環節，它們的參數都需要進行整定，并且很多參數之間相互聯系，為確定各組成部分的參數，可以分別對這部分進行參數整定。先對TD進行參數設定，然后依次對 ESO 和NLSEF 進行參數設定。由于參數整定的關鍵是正確理解各個參數的物理意義，因此，韓教授以fhan函數為非線性組合函數的ADRC算法中需要整定的參數進行了說明。他提出，三個參數c，h1，b0與PID的三個增益類似，1/h1相當于PID的比例增益，阻尼因子c相當于PID的微分增益;補償因子b0相當于控制量增益，類似于PID積分增益。

把保證閉環性能的PID參數的依賴關系比作漏斗效應，則閉環性能對ADRC參數的依賴關系比作盆地效應，保證閉環性能的自抗擾控制器參數適應范圍大，同時在很多大范圍內參數變化對自抗擾控制器的性能影響不大，需要注意的是應盡可能地將參數調到盆地中間位置[3]。

3系統仿真結果

上文進行了四旋翼飛行器的原理分析，針對這樣一個非線性二階系統設計了自抗擾解耦控制器，本節將在simulink平臺上搭建仿真模型，對其的各項性能進行仿真實驗和結果分析。

3.1 穩定性仿真

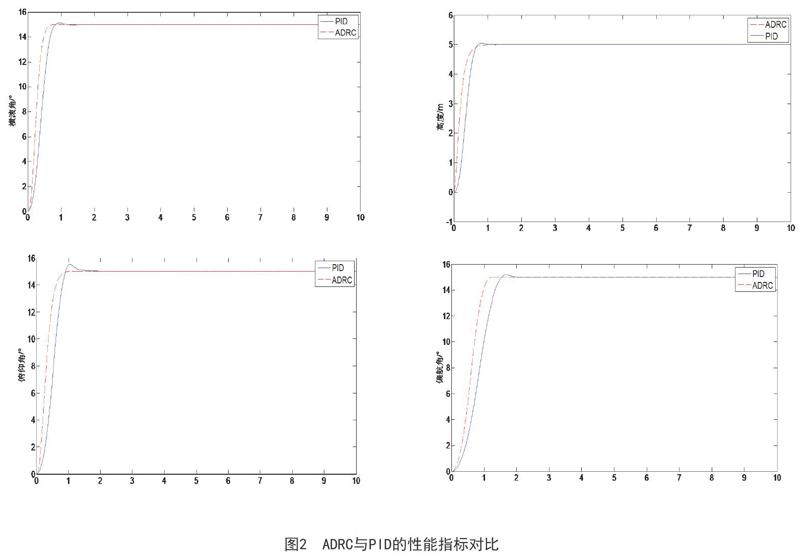
首先將對基于自抗擾控制的四旋翼飛行器進行穩定性實驗和分析，設定各通道初始值為0，高度期望值設為5m，俯仰角、橫滾角、偏航角的期望值為15° ，控制的目的是使四旋翼飛行器實現各種姿態穩定。仿真結果如下：

與PID控制器性能對比：

3.2 抗擾性仿真

抗擾性指的是系統對于外界的干擾所受影響的程度。在實際的四旋翼飛行系統中會受到外界各種情況的干擾，在穩定性試驗基礎下進行如下仿真實驗，統一在3s時刻加入噪聲信號（模擬）作為外界干擾，測試個通道控制器的抗擾性能[4]。仿真結果如下：

從以上實驗可以看出對于外部的擾動，各通道都能在自抗擾控制器控制下1秒內恢復穩定狀態，抗擾性較為優異。因為ESO擴展狀態觀測器能夠快速的估計擾動，并對控制系統進行補償，達到消除擾動的效果。擴展狀態觀測器估計出系統的總擾動實施作用量，可以對系統進行補償，從而很好的抑制外部干擾[5]。

3.3 魯棒性仿真

魯棒性指的是系統對于自身內部的改變所受影響的程度。在現實中四旋翼飛行器的系統系統性能和參數的變化通常都是無法規避的。魯棒性主要體現的是當模型參數發生較大改變時，控制器能否繼續保持良好的控制性能。因此，在穩定性實驗基礎上，對控制器進行魯棒性的檢驗。分別對四旋翼飛行器的參數（各坐標軸轉動慣量和機體質量等參數）增大和減小30%，對各通道進行原系統對比實驗[6]，為方便觀察，原系統延遲0.2s，結果如下：

從上面的仿真圖和性能指標可以看出，在原系統ADRC控制器參數沒有改變的情況下，增大或減小30%系統參數后，除橫滾通道發生一定偏移外，其他通道幾乎與原系統重合，性能參數沒有太大的變化。經過分析和探究，橫滾通道控制器的參數需要繼續優化，可以保證控制的性能。這說明了自抗擾控制器有較強的魯棒性。也說明了自抗擾控制器對控制對象精度沒有很高的要求。

通過仿真實驗驗證將自抗擾控制技術應用于四旋翼飛行器控制系統有著良好的效果，可以實現姿態和高度的穩定控制，ADRC具有超調量小，調節時間短，抗擾性和魯棒性強的優點[7]。

4結束語

根據對四旋翼自抗擾控制系統的穩定性實驗，抗擾性實驗，和魯棒性實驗，表明自抗擾控制器不僅能夠有效估計系統內外擾動并補償消除其影響，實現對四旋翼穩定的控制。還有較強的魯棒性。相比經典PID控制的性能有了顯著的提升，可以很好地滿足四旋翼飛行器對控制器性能的要求。實驗中的難點主要在于非線性自抗擾控制器的參數過于繁多，而且目前學術界還沒有形成完備的整定方法，參數調節主要依賴于試湊法，整定過程復雜，工作量過大。在以后的研究試驗當中可以考慮使用線性自抗擾控制技術，減少參數的數目，但依然可以保留經典自抗擾控制器的優點。

從本文的研究實驗可以清楚地看出自抗擾控制器具有優秀的主動抗擾能力，在四旋翼飛行器飛行控制上所體現的優越性。繼續優化自抗擾控制器，將在工程系統控制中獲得更優秀的控制性能。

參考文獻

[1] 周權，黃向華，朱理化.四旋翼微型飛行平臺姿態穩定控制試驗研究[J].傳感器與微系統，2009（5）：72-74.

[2] 周宣征，張寶國.自抗擾控制器的參數整定研究[J].電氣自動化，2014（2）：23-24.

[3] 張廣昱，袁昌盛.基于自抗擾理論的小型四旋翼飛行器姿態控制[J].航空工程進展，2014（3）：338-342.

[4] 王辰昱.自抗擾控制器的參數整定及應用[D].北京：華北電力大學，2010.

[5] 高志強.自抗擾控制思想探究[J].控制理論與應用，2013（12）：1498-1510.

[6] 孟凡東.自抗擾控制器的設計與應用研究[D].哈爾濱：哈爾濱理工大學，2009.

[7] 陳增強，李毅，袁著祉，等.串級自抗擾控制器在縱列式雙旋翼直升機飛行姿態控制中的應用[J].控制理論與應用，2015（9）：1219-1225.

作者簡介

李定聰（1995-），男，云南曲靖人;畢業院校：中北大學，專業：自動化，學歷：本科，現就職單位：綿陽市維博電子有限責任公司，研究方向：智能測控。

龐中秋（1990-），男，河北滄州人;畢業院校：廣西師范大學 專業：微電子，學歷：碩士，現就職單位：綿陽市維博電子有限責任公司，研究方向：智能傳感。