二維各向異性多孔材料多軸蠕變行為的數值模擬

劉浩偉，蘇步云,2,3，邱 吉，李志強,2,3

（1. 太原理工大學機械與運載工程學院應用力學研究所，山西 太原 030024；2. 材料強度與結構沖擊山西省重點實驗室，山西 太原 030024；3. 力學國家級實驗教學示范中心（太原理工大學），山西 太原 030024）

多孔材料因具有比強度高、吸能優良、抗震性能好等優良特性，在汽車和飛機結構的輕量化設計、防護包裝、換熱器等領域具有廣闊的應用前景。值得注意的是，大多數多孔材料經常在高溫環境下長期服役[1-2]，在此條件下必須考慮其蠕變行為的影響。因此，建立合適的多孔材料蠕變本構模型尤為重要。合適的蠕變本構模型能夠使設計變得更加合理，進而延長部件的使用壽命。

為了研究多孔材料的蠕變行為，Andrews 等[3]、Hodge 等[4]分別基于彎曲主導的立方模型和軸壓主導的多孔材料模型，推導了開孔蜂窩材料的單軸穩態蠕變速率。盧子興等[5]通過對Warren 等[6]的正四面體模型支柱節點處的體積進行修正，得到了一種新的四面體模型，并將其用于預測相對密度較大的多孔材料蠕變性能。

隨著數值模擬技術的發展，有限元分析（Finite element analysis，FEA）越來越多地被應用于多孔材料蠕變行為研究中。Andrews 等[7]模擬了二維Voronoi 模型的穩態蠕變率，分析了邊界條件和胞壁曲率對單軸蠕變行為的影響，結果表明：細觀結構對多孔材料的蠕變速率和壽命有顯著影響，其中胞壁曲率對蠕變速率的影響最大，胞孔形狀和大小的分布也影響蠕變速率。Oppenheimer 等[8]構建了具有不同微觀結構的單元胞體模型，比較了不同應力狀態下多孔材料的應力分布特征和變形機理。Huang 等[9]提出了一種利用具有周期性邊界條件的三維Voronoi 模型確定理論公式參數的方法。Zhu 等[10]用線性黏彈性理論分析了開孔低密度聚合物多孔材料的高應變蠕變行為，使用Kelvin 模型模擬了聚氨酯泡沫的微觀結構，通過測量應力、松弛模量和密度預測壓縮蠕變曲線，結果表明，當胞元的邊發生非線性變形時，蠕變速率會加快。Su 等[11]利用二維蜂窩和三維十四面體模型研究了缺陷對蜂窩材料蠕變行為的影響，提出了一種預測蜂窩材料單軸蠕變率的經驗模型，該模型是不同類型缺失棱壁比例的函數。

在實際工程應用中，材料經常處于復雜的應力狀態[12]；而且，許多天然多孔材料，如木材、骨頭等均表現出明顯的各向異性[1-2,13]；此外，對于大多數人工多孔材料，在發泡過程中其微觀結構會不可避免地在上升方向被拉長，從而導致多孔材料呈各向異性。Su 等[14]利用三維Voronoi 模型，研究了橫觀各向同性多孔材料的多軸蠕變行為，建立了多孔材料的唯象蠕變本構模型。然而，目前關于多孔材料蠕變行為的研究大多集中在各向同性材料及其單軸蠕變行為上，各向異性多孔材料及其多軸蠕變行為的研究[15-17]非常少。基于此，本研究擬通過建立有限元模型來研究二維各向異性多孔材料的多軸蠕變行為，推導相應的本構模型，進而為實際工程應用提供理論指導。

1 有限元模型建立

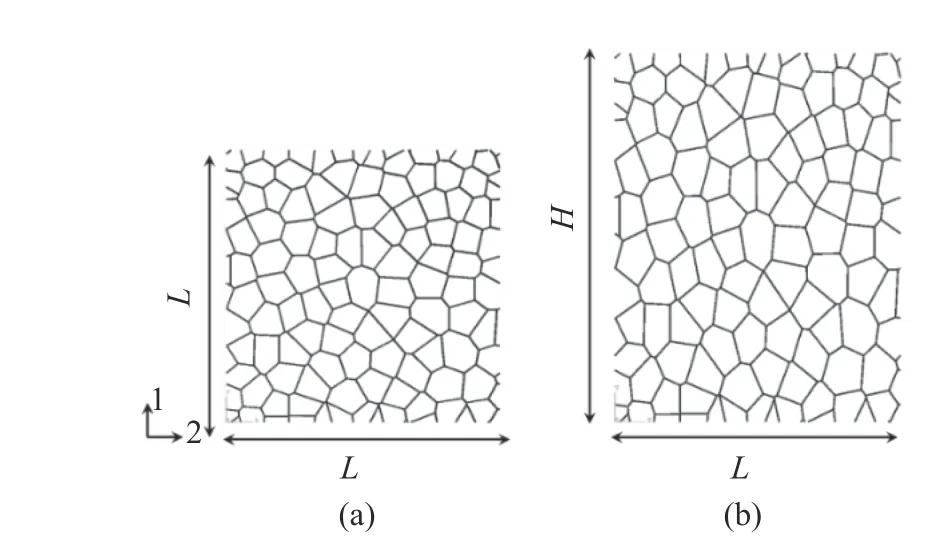
圖1 二維各向異性多孔材料有限元模型的建立Fig. 1 Establishment of finite element model of 2D anisotropic cellular material

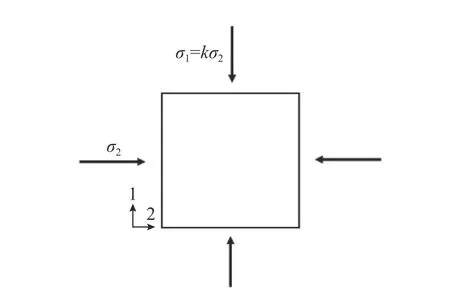
圖2 二維多孔材料多軸加載示意圖Fig. 2 Schematic of 2D cellular material under multiaxial loading

2 模擬結果及分析

2.1 各向異性程度對單軸蠕變行為的影響

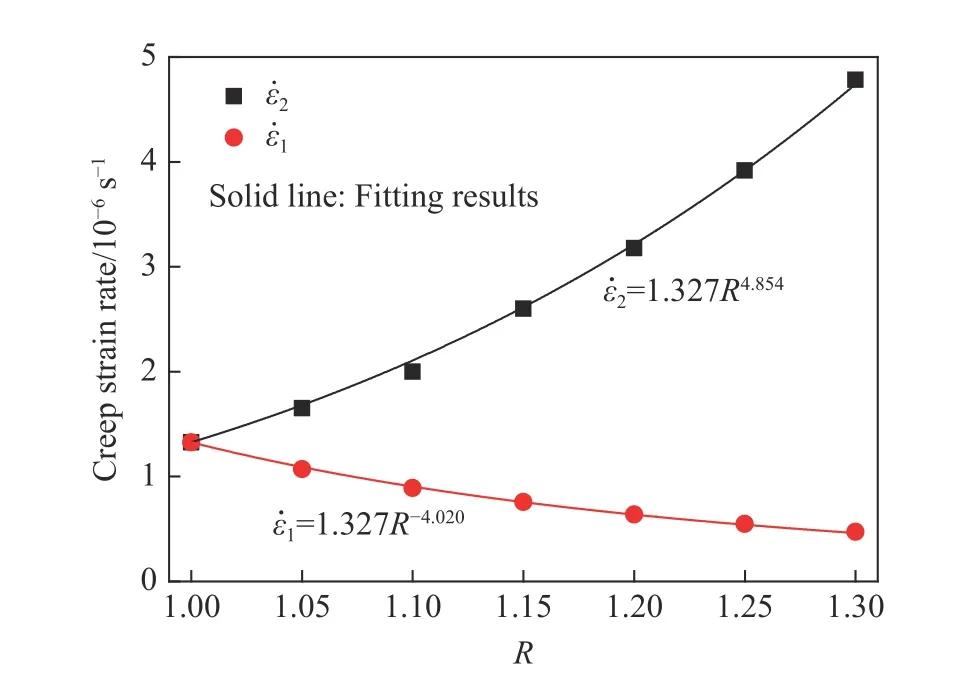
圖3 二維各向異性多孔材料在不同方向的穩態蠕變率Fig. 3 Steady creep strain rate of 2D anisotropic cellular material in different directions

圖3 給出了Voronoi 隨機模型在不同方向上的穩態蠕變率隨材料各向異性程度R的變化趨勢，其中：有限元模擬結果用數據點表示，擬合結果用實線表示。

從圖3 中可以明顯地看出：隨著R的增大，沿方向1 的穩態蠕變率（ ε˙1）減小，而沿方向2 的穩態蠕變率（ ε˙2）增大，單軸蠕變性能表現出明顯的各向異性。同時從圖3 還可以看出，不論是 ε˙1還是ε˙2，均呈現出冪函數形式的變化趨勢。因此，采用冪函數來描述二維各向異性多孔材料在不同方向上單軸穩態蠕變率的變化規律，擬合結果見圖3。

2.2 各向異性程度對多軸蠕變行為的影響

2.2.1 多孔材料多軸蠕變本構模型的建立

可見，模擬結果與擬合函數具有非常好的一致性，進一步證明了所用擬合函數的合理性。

為了驗證本研究所建立的二維各向異性多孔材料蠕變模型的有效性，將擬合得到的彈塑性參數代入蠕變模型中，通過大量的有限元數值模擬對其進行有效性驗證。所有模擬工況可分為以下兩類：（1）令R=1.0，k在-1.0～1.0 區間變化，結果如圖5(a)所示；（2）令k=0.5，R在1.0～1.3 區間變化，結果如圖5(b)所示。可以看出：對于第1 類工況，隨著k的增大，方向1 的穩態蠕變率逐漸減小，且當k＞ 0 時，下降趨勢逐漸變緩；對于第2 類工況，當R從1.0 增大到1.3 時，方向1 的穩態蠕變率從1 × 10-7s-1逐漸降低。顯然，該理論模型能有效預測各向異性多孔材料的多軸蠕變行為。

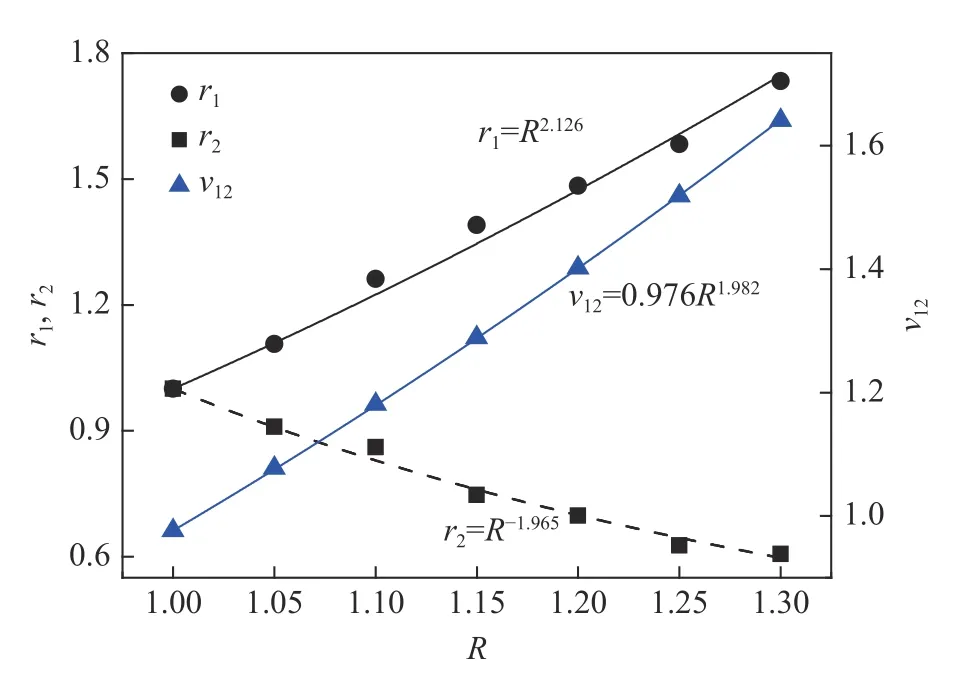
圖4 彈塑性參數擬合結果Fig. 4 Elastoplastic parameter fitting results

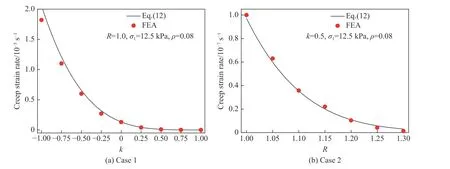
圖5 理論模型與有限元分析結果對比Fig. 5 Comparison of the phenomenological model and the FEA results

3 結 論

對二維各向異性多孔材料進行了大量的多軸蠕變數值模擬，通過引入幾何拉伸系數R，分析了各向異性程度對彈塑性參數和多軸穩態蠕變率的影響。結果表明：r1和 ν12隨著R的增大而增大，而r2隨R的增大而減小；當R從1.0 增大到1.3 時，方向1 的穩態蠕變率逐漸降低，而方向2 的穩態蠕變率呈相反的變化趨勢。基于特征應力-特征應變關系，提出了一個能表征二維各向異性多孔材料多軸蠕變行為的本構模型。理論與數值模擬結果對比顯示，兩者具有較高的吻合程度，證明了該唯象模型的有效性。