基于組合神經網絡模型的新冠疫情傳播預測分析

吳志強 王波

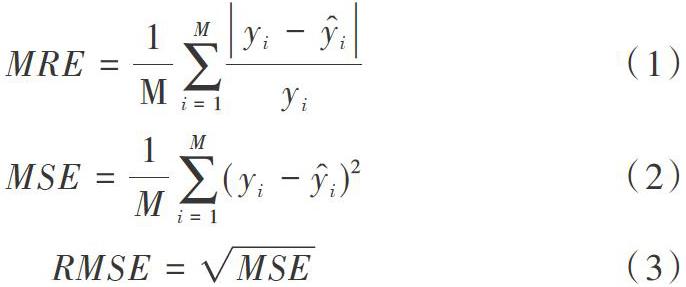
摘 要：在全球抗擊新型冠狀病毒肺炎（COVID-19）疫情的過程中，合理的疫情傳播預測對于疫情防控有重要參考意義。為了對病毒傳播進行合理預測，針對傳統疫情傳播預測模型存在的不足，提出一種組合式神經網絡的疫情傳播預測模型，并將其應用于湖北省1月29日-3月15日每日新增確診人數預測及湖北省每日累計確診人數預測。預測結果分析顯示，該神經網絡預測模型預測結果可靠有效。模型性能分析結果表明，組合式神經網絡預測模型平均相對誤差（MRE）不超過0.16，均方誤差（MSE）不超過0.1，均方根誤差（RMSE）為0.262 9，性能明顯優于其它幾種神經網絡預測模型。基于武漢市與廣東省疫情傳播預測的實證結果顯示模型具有較好的適用性及準確性。

關鍵詞：新型冠狀病毒肺炎;組合神經網絡預測模型;疫情傳播;預測分析

DOI：10. 11907/rjdk. 201884

中圖分類號：TP301 文獻標識碼：A 文章編號：1672-7800（2020）010-0015-05

Abstract：In the global fight against COVID-19， reasonable prediction of the spread of the epidemic has important reference significance for the prevention and control of the epidemic. In order to reasonably predict the spread of COVID-19， considering the shortcomings of traditional epidemic spread prediction models， this paper proposes a combined neural network epidemic spread prediction model. Subsequently， the model is applied to predict the daily number of newly diagnosed patients in Hubei Province and the cumulative number of daily diagnoses from January 29 to March 15. The analysis of prediction results shows that the prediction results of each neural network prediction model are reliable and effective. The model performance analysis results show that the combined neural network prediction model has an MRE of no more than 0.16， an MSE of no more than 0.1 and an RMSE of 0.262 9， which means that the performance of the combined neural network is significantly better than that of other neural network prediction models. The empirical results based on Wuhan city and Guangdong Province show that the model has good applicability and accuracy.

Key Words：COVID-19;combined neural network prediction model;the spread of the epidemic; forecast analysis

0 引言

2019年12月以來，新型冠狀病毒肺炎（COVID-19）疫情爆發，其傳染性強、傳播迅速。在全球抗擊新冠肺炎的過程中，相關科研人員對疫情傳播和發展趨勢進行了大量研究，為疫情防控提供了重要的參考信息[1-2]。

國內外學者針對疫情傳播與發展趨勢預測分析，構建的預測模型主要集中于動力學模型及統計學模型。動力學模型根據各要素之間的聯系構建相關動力學微分方程，進而可模擬相關要素發展趨勢，因此被廣泛應用于疾病傳播和分析，新型冠狀病毒肺炎傳播的動力學模型主要有SIR模型[3-6]、SEIR模型[7-10]、SEIHR模型[11]、SEQIR模型[12]等。如Zareie 等[3]通過構建伊朗COVID-19疫情的SIR模型，對伊朗COVID-19疫情傳播進行有效預測;盛華雄等[4]在對疫情數據預處理的基礎上，在控制階段運用經典SIR模型與差分遞推方法進行疫情傳播分析和預測;魏永越等[8]基于改進的SEIR模型對新型冠狀病毒肺炎疫情進行趨勢預測;唐三一等[11]通過建立SEIHR模型對新型冠狀病毒肺炎疫情進行預測，進而給出相關防控策略。

統計學模型基于邏輯回歸模型挖掘統計數據相關規律，進而用于疫情傳播預測分析。Ahmed 等[13]利用Logistic模型對土耳其和伊拉克疫情規模進行預測，預測結果驗證了模型有效性;Li 等[14]基于官方疫情數據，將高斯理論用于研究COVID-19傳播過程;盛華雄等[4]在對疫情數據預處理的基礎上，在自由傳播階段運用Logistic模型，比較分析提前5天或延后5天的疫情數據與實測數據，說明及時采取防疫措施的重要性。

除此之外，多層感知機模型[15]、人工智能模型[16-17]、社會現象學模型[18-19]等也被相關學者應用于國外疫情傳播預測分析。盡管通過上述預測模型可得出有效的疫情傳播預測結果，然而無論是動力學模型還是統計學模型，均僅通過設置好的預測參數進行疫情預測，當參數過多時將面臨求解困難、復雜的問題，且未考慮疑似人群在疫情傳播中的影響;而相關人工智能模型（如多層感知機）容易陷入局部極小點問題，且國內與疫情傳播相關的智能預測模型研究較少。因此，本文提出一種組合式神經網絡的疫情傳播預測模型，將粒子群用于神經網絡訓練過程，并將其應用于湖北省1月29日-3月15日的疫情傳播預測。

1 組合神經網絡預測模型

1.1 基本假設與數據說明

為對湖北省疫情傳播作出合理的預測分析，提出5項基本假設：①國家衛健委提供的疫情數據真實可靠;②除確診人數、死亡人數對疫情傳播有直接影響外，疑似人群及重癥人數對疫情傳播也存在相關聯系;③治愈人群可能產生再次感染，即治愈人數與疫情傳播依舊存在聯系;④只用前1天的相關數據預測后1天的疫情新增確診量;⑤考慮到2月12 號推出用于診斷疫情的相關試劑，湖北省新增確診人數急劇上升至14 840例，因此該日湖北省新增確診人數采用文獻[4]中推理出的數據（新增確診人數2 051例）替代。

其中，t表示時間序列（1表示1月29號，以此類推），I表示每日新增確診人數，N表示每日累計確診人數，R表示每日治愈人數，D表示每日死亡人數，S表示每日疑似人數，Z表示每日重癥人數。本文數據來源為國家衛健委提供的每日疫情數據，網址為http：//www.nhc.gov.cn/xcs/xxgzbd/gzbd_index.shtml。選取湖北省1月28日-3月15日的疫情數據，數據內容包含上述數據內容。

1.2 模型介紹

神經網絡模型具有自學習能力、自適應能力、非線性映射能力及容錯率高等優點，應用廣泛，且可根據輸入輸出映射進行自我調整，因此可被用于疫情傳播預測分析。考慮到不同的激活函數及神經網絡結構對神經網絡性能及預測精度有重要影響，因此本文構建4種不同的神經網絡模型對湖北省疫情每日新增確診人數進行預測，并將4種神經網絡預測結果作為傳統多層感知機的輸入進行擬合預測。考慮到傳統神經網絡在權值訓練過程中容易陷入局部極小點且收斂較慢，因此將粒子群算法用于各神經網絡權重訓練，其中各神經網絡參數如表1所示。

考慮到傳統神經網絡在權值訓練過程中容易陷入局部極小點且收斂較慢，將粒子群算法用于各神經網絡權重訓練，訓練過程為：①初始化粒子群基本參數，最大迭代次數為1 000次，粒子為各神經網絡連接權值;②將粒子代入各神經網絡，將各神經網絡輸出與目標輸出的殘差作為粒子群算法的目標函數;③更新粒子，并計算粒子目標值，并根據目標值大小進行更新最優粒子和最優值;④判斷是否滿足停止條件，若滿足則輸入最佳粒子，若不滿足返回步驟2。

2 疫情傳播預測分析

2.1 湖北省每日新增確診量預測

選取湖北省1月28日-3月15日疫情數據進行疫情傳播預測分析，數據信息包括：每日疫情新增確診人數I、每日治愈人數R、每日死亡人數D、每日新增疑似人數S、每日重癥人數Z以及每日累計確診人數N（數據來源國家衛健委）。將前1天的疫情數據作為神經網絡輸入，后1天疫情新增確診人數作為神經網絡輸出，進行湖北省每日新增確診量預測分析，各神經網絡預測結果如表2所示，其中時間1表示1月29日。

其中2月12號（第15時間序列）新增確診量用文獻[4]數據替代，最后時間序列的多個神經網絡預測結果為負值，故而上進為0，根據表2所得的新增確診人數預測結果得到湖北省每日新增確診人數預測，如圖2所示。

由圖2可知，以上5種神經網絡對于湖北省每日新增確診人數的預測與實際趨勢均較為符合，可對湖北省每日新增確診人數進行有效的預測分析，但是在某些時間節點上仍存在差異，如第20時間節點上神經網絡2（雙曲三層神經網絡）及神經網絡3（四層神經網絡）的預測結果與實際新增確診人數存在較大差異。同時，在5種神經網絡預測模型中，神經網絡1（三層神經網絡）及組合預測模型對于湖北省每日新增確診人數預測精度較高。

2.2 湖北省每日累計確診量預測

合理有效地預測分析湖北省每日累計確診量可以為疫情拐點的出現及疫情的有效控制提供參考。由于[Nt=Nt-1+It-Rt-Dt]（第t時刻累計確診量由第t-1時刻的累計確診量、第t時刻新增確診量、第t時刻新增治愈量以及第t時刻新增死亡量遞推而出），因此基于上述湖北省每日新增確診量預測分析，可以進行湖北省每日累計確診量預測分析，分析結果如表3所示。

根據表3所得的湖北省每日累計確診量預測結果，得到湖北省每日累計確診量預測趨勢，如圖3所示。

由圖3可知，各神經網絡預測模型對于湖北省每日累計確診量預測結果均較為理想，其預測趨勢與實際趨勢貼合較近，能夠有效反映湖北省每日累計確診量。從圖3可以看出，湖北疫情每日累計確診量在第23時刻（2月19號）左右出現下降趨勢，即意味著湖北省疫情拐點出現，同時在第16時刻（2月12號）左右，湖北疫情每日累計確診量急劇增加，由于在2月12號左右推出用于診斷疫情的相關試劑，湖北省新增確診人數急劇上升。

3 預測結果分析

3.1 預測誤差分析

由湖北省每日累計確診量預測結果（見表2）可以得到各預測模型在各時刻下與實際新增確診量的偏差，進而得到各模型在各時刻下預測偏差分布，如圖4所示。

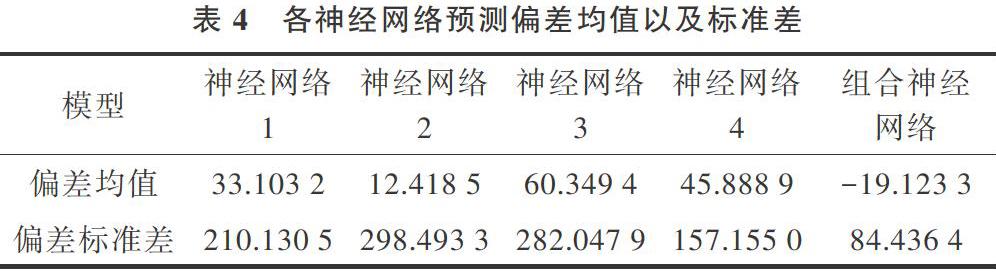
由圖3可知隨著時間序列t 的推移，各神經網絡對于湖北省每日新增確診量預測偏差逐漸減少趨近于0，表明各神經網絡對于湖北省每日新增確診量預測結果有效。為檢驗各模型預測結果可靠性，各神經網絡對于湖北省每日新增確診量預測偏差均值及標準差如表4所示。

由表4可知，神經網絡2與組合式神經網絡與其它3種神經網絡相比，偏差均值更低，然而從偏差標準差的角度來看，組合式神經網絡預測偏差標準差為84.436 3，較其它4種神經網絡預測結果更加可靠。

3.2 模型性能分析

模型性能評估是檢驗模型能否用于疫情傳播預測的直觀指標，而平均相對誤差（MRE）、均方誤差（MSE）以及均方根誤差（RMSE）是評估神經網絡的重要指標，因此本文利用這3種指標對各神經網絡預測模型進行評估，其中各指標計算公式如式（1）—式（3）所示。

其中[yi]表示第i時刻的實際量，[yi]表示第i時刻的預測量，M表示預測樣本量。

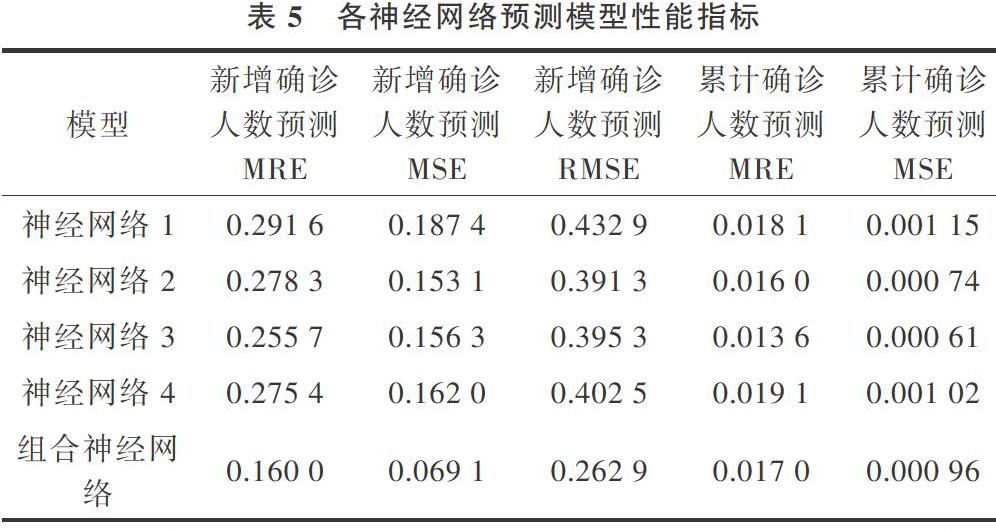
根據式（1）—式（3）分別求得各神經網絡預測模型在湖北省每日新增確診量預測中的MRE、MSE、RMSE及在湖北省每日累計確診量預測中的MRE與MSE，如表5所示。

根據表5各神經網絡預測模型指標得分，構建各神經網絡預測模型性能雷達圖，如圖5所示。通過對比各神經網絡預測模型評價指標得分可知，神經網絡預測模型對于湖北省疫情傳播預測精度較好（新增確診人數預測MRE均小于0.3，累計確診人數預測MRE均小于0.02）;根據MRE評價指標來看，組合神經網絡預測模型及神經網絡3（4層神經網絡預測模型）較之其它3種神經網絡預測模型預測精度更高;根據MSE評價指標來看，組合神經網絡預測模型性能最優，神經網絡2（雙曲3層神經網絡預測模型）與神經網絡3（四層神經網絡預測模型）預測性能相當;根據RMSE評級指標可以看出組合神經網絡預測模型性能優于其它4種神經網絡預測模型，預測結果精度更高。綜合各個評價指標來看，根據各神經網絡在性能雷達圖上所屬面積可以看出，組合神經網絡預測模型性能優于其它4種神經網絡模型，其次是神經網絡3（4層神經網絡預測模型）、神經網絡2（雙曲3層神經網絡預測模型）、神經網絡4（雙曲4層神經網絡預測模型）以及神經網絡1（3層神經網絡預測模型）。

3.3 模型適應性分析

為驗證組合式神經網絡適用性及準確性，采用湖北省武漢市2月12日-3月12日疫情數據及廣東省2月1日-2月22日疫情數據用于實驗驗證，驗證結果如圖6所示。

由實驗驗證結果可以看出，組合式神經網絡預測模型能較好地預測武漢市及廣東省疫情傳播趨勢，當訓練數據充分時，組合式神經網絡預測模型具有較好的適用性。從準確性角度出發，組合式神經網絡預測模型對于武漢市與廣東省新增確診人數預測的MRE均小于20%，其中武漢市新增確診人數預測MRE為6.01%，廣東省新增確診人數預測MRE為17.25%;對于武漢市以及廣東省累計確診人數預測的MRE均小于3%，其中武漢市累計確診人數預測MRE為2.09%，廣東省累計確診人數預測MRE為0.65%。由此可見，在數據集充分的情況下，組合式神經網絡預測模型有著較高的預測精度。

4 結語

針對傳統疫情傳播預測方法存在的不足，本文提出了一種基于組合式神經網絡的疫情傳播預測模型，并將其應用于湖北省每日新增確診人數預測以及湖北省每日累計確診人數預測。預測結果顯示，神經網絡預測模型預測結果可靠有效。模型性能分析結果表明，組合式神經網絡預測模型性能明顯優于其它4種神經網絡預測模型，預測性能更佳。武漢市與廣東省數據實證結果表明，組合式神經網絡預測模型適應性較強、準確性較高。但是，神經網絡優化仍依賴于智能優化算法權值優化。在未來研究中，一方面需加強智能優化算法與神經網絡算法的結合，另一方面將積極探索合適的方法對神經網絡進行結構優化，提升其實際應用性能。

參考文獻：

[1] ANIRUDH A. Mathematical modeling and the transmission dynamics in predicting the Covid-19——What next in combating the pandemic[J]. Infectious Disease Modelling，2020（5）：366-374.

[2] MOHAMADOU Y， HALIDOU A， KAPEN T. A review of mathematical modeling， artificial intelligence and datasets used in the study， prediction and management of COVID-19[J]. Applied Intelligence， 2020（7）：1-13.

[3] ZAREIE B，MOHAMMAD A R，MANSOURNIA A， et al. A model for COVID-19 prediction in Iran based on China parameters[J]. Archives of Iranian medicine， 2020， 23（4）：244-248..

[4] 盛華雄，吳琳，肖長亮. 新冠肺炎疫情傳播建模分析與預測[J]. 系統仿真學報，2020，32（5）：759-766.

[5] 張艷霞，李進. 基于SIR模型的新冠肺炎疫情傳播預測分析[J]. 安徽工業大學學報（自然科學版），2020，37（1）：94-101.

[6] 汪劍眉，李鋼. 新冠肺炎非均勻感染力傳播模型與干預分析[J]. 電子科技大學學報，2020，49（3）：392-398.

[7] 范如國，王奕博，羅明，等. 基于SEIR的新冠肺炎傳播模型及拐點預測分析[J]. 電子科技大學學報，2020，49（3）：369-374.

[8] 魏永越，盧珍珍，杜志成，等. 基于改進的SEIR～（+CAQ）傳染病動力學模型進行新型冠狀病毒肺炎疫情趨勢分析[J].中華流行病學雜志，2020（4）：470-475.

[9] 游光榮，游翰霖，趙得智，等. 新冠肺炎疫情傳播模型及防控干預措施的因果分析評估[J]. 科技導報，2020，38（6）：90-96.

[10] RAJAGOPAL K，HASANZADEH N，PARASTESH F，et al. A fractional-order model for the novel coronavirus （COVID-19） outbreak[J]. Nonlinear Dynamics，2020（6）：1-8.

[11] 唐三一，肖燕妮，彭志行，等. 新型冠狀病毒肺炎疫情預測建模、數據融合與防控策略分析[J]. 中華流行病學雜志，2020（4）：480-484.

[12] MANDAL M， JANA S， NANDI S K，et al. A model based study on the dynamics of COVID-19： prediction and control[J].? Chaos， Solitons and Fractals： the Interdisciplinary Journal of Nonlinear Science， and Nonequilibrium and Complex Phenomena，2020，136：109889.

[13] AHMED A，ABDULLAH B，MOHAMMAD M A，et al. Analysis coronavirus disease （COVID-19） model using numerical approaches and logistic model[J].? AIMS Bioengineering，2020，7（3）： 130-146.

[14] LI L，YANG Z，DANG Z，et al. Propagation analysis and prediction of the COVID-19[J].? Infectious Disease Modelling，2020，5：282-292.

[15] CAR Z，EGOTA S B， ANELI N， et al. Modeling the spread of COVID-19 infection using a multilayer perceptron[DB/OL].? Computational and Mathematical Methods in Medicine：1-10.2020-05-29.https：//www.hindawi.com/journals/cmmm/2020/5714714/.

[16] CHIMMULA V K R，ZHANG L. Time series forecasting of COVID-19 transmission in Canada using LSTM networks[J].? Chaos Solitons & Fractals， 2020，135：109864.

[17] ZHENG N，DU S，WANG J， et al. Predicting COVID-19 in China using hybrid AI model[J]. IEEE Transactions on Cybernetics，2020， 99：1-14.

[18] ROOSA K，LEE Y，LUO R，et al. Short-term forecasts of the COVID-19 epidemic in Guangdong and Zhejiang， China： February 13-23， 2020[J].? Journal of Clinical Medicine，2020，9（2）：596-604.

[19] DUFFEY R B，ZIO E. Prediction of CoVid-19 infection， transmission and recovery rates： a new analysis and global societal comparisons[J].? Safety Science， 2020，129：104854.

（責任編輯：江 艷）