基于ANSYS的三閉式SMA混雜復合材料箱型薄壁梁的模態分析
,,
(青島科技大學機電工程學院,山東 青島 266061)
0 引言
風力機葉片是風力發電機的關鍵部件,其本身是一個柔性細長體,很容易受到外部動力激勵,如風載荷和地震載荷。當這些載荷不間斷地作用在風力機葉片上,導致風力機葉片產生振動,而振動對風力機葉片的壽命產生很大的影響,甚至可能導致風力機完全損壞,進而影響風能的轉換。
大型風力機葉片具有多閉式復合材料箱型薄壁梁的特征。復合材料薄壁梁由于其具有高比強度,高比模量和質量輕的特性而被廣泛應用于工程結構,無論是在直升機旋翼槳葉還是在風力機葉片上,都普遍采用復合材料薄壁梁的結構形式。由于復合材料薄壁梁在實際工程應用中的受力狀態和變形都很復雜,存在著載荷耦合,結構彈性耦合、非線性的大變形大撓度等力學行為[1],使得大型風力機葉片的動力學問題的求解變得更為復雜。智能結構集傳感器、控制器、作動器與結構于一體,目前得到較多關注。智能材料在風力機葉片顫振與振動智能控制中的應用鮮有報道[2]。將智能材料粘貼在葉片的表面或埋入葉片內部,從而使葉片產生一個小的扭曲變形或者改變其氣動特性。目前,智能材料在復合材料薄壁結構中的應用主要集中在將壓電傳感器和壓電驅動器埋入復合材料結構中制成夾心材料對其振動進行主動控制[3-7]。然而,利用SMA智能材料在復合材料薄壁結構的振動特性研究[8-12],國內外的報道尚不多見。
1 模態分析的有限元基本方程
模態分析是研究結構動力特性一種近代方法,是系統辨別方法在工程振動領域中的應用。模態是機械結構的固有振動特性,每一個模態具有特定的固有頻率、阻尼比和模態振型。基于有限元法的結構動力學平衡方程為

(1)


(2)
設{u}={φ}eiωt代入式(2)得
[K]{φ}=ω2[M]{φ}
(3)
令λ=ω2為特征值,{φ}為特征向量,則
([K]-λ[M]){φ}=0
(4)
若{φ}存在非零解,必有
det|[K]-λ[M]|=0
(5)
可解得特征值(固有頻率)λ1、λ2···、λi和特征向量(振型){φi}。
2 SMA混雜復合材料箱型薄壁梁的有限元建模
考慮一端固定一端自由的SMA混雜復合材料三閉式箱型薄壁梁,其外形結構及有限元模型如圖1和圖2所示。箱型梁的尺寸采用文獻[14]的結構尺寸,其中L=1.500 m,a=0.075 m,b=0.025 m。

圖1 三閉式箱型薄壁梁的結構模型

圖2 薄壁梁的有限元模型
2.1 建立SMA混雜復合材料箱型薄壁梁有限元模型
在Pro/ENGINEER軟件中建立箱型薄壁梁的曲面模型,導入ANSYS WorkBench中的Geometry,然后在ANSYS ACP模塊中進行網格劃分,定義復合材料鋪層信息,其中包括鋪層順序、鋪層材料屬性、鋪層的厚度以及鋪層的方向角等。
考慮復合材料層合板2種常見的剛度配置方式,一種是周向均勻配置方式(簡稱CUS),另一種是周向反對稱剛度配置方式(簡稱CAS)。2種鋪層方式如圖3所示。對2種剛度配置方式分別建立有限元模型。
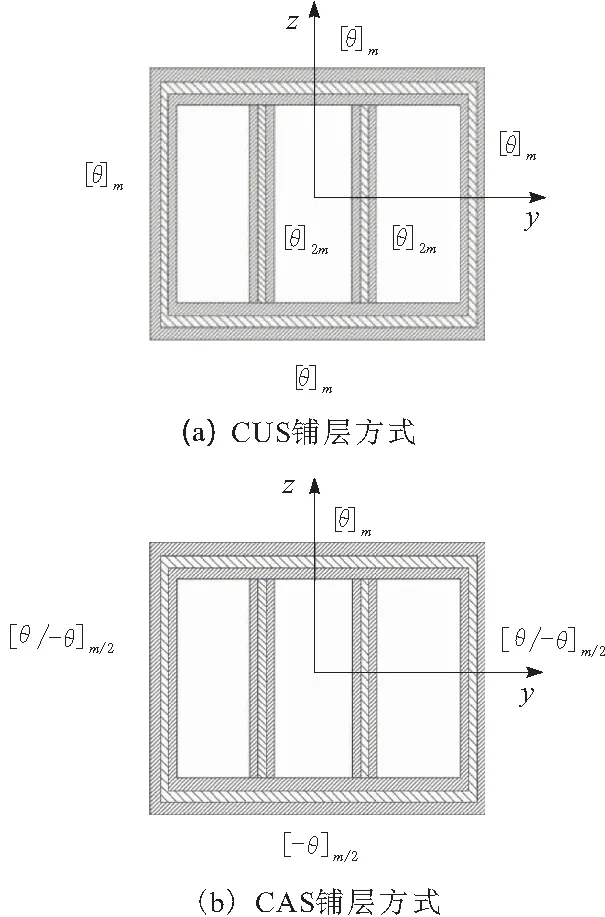
圖3 三閉式箱型薄壁梁鋪層方式
2.2 材料選擇
針對壁面為6層SMA/石墨/環氧樹脂箱型薄壁梁,石墨/環氧樹脂材料參數采用文獻[14]的材料參數,其材料參數如表1所示。石墨/環氧樹脂材料各個方向的彈性模量用分別EX、EY、EZ表示,各個方向的剪切模量用Gxy、Gxz、Gyz表示,各個方向的泊松比用PRxy、PRxz、PRyz表示。

表1 石墨/環氧樹脂材料參數
ANSYS軟件在其材料屬性中提供了SMA模型,用來模擬SMA材料偽彈性的本構模型是基于Auricchio F本構模型[15]得到的,能夠實現SMA超彈性的模擬。ANSYS軟件在定義SMA材料屬性時,需要指定7個參數:即C1為馬氏體相變開始應力;C2為馬氏體相變結束應力;C3為馬氏體逆相變開始應力;C4為馬氏體逆相變結束應力;C5為最大殘余應變;C6為反映拉壓差異的參數;C7為馬氏體彈性模量。在模擬計算之前,要先確定這些參數。SMA絲在ANSYS中的材料相變參數如表2所示。

表2 SMA在ANSYS中材料相變參數
利用ANSYS WorkBench中的Material Designer模塊建立SMA/石墨/環氧樹脂單層板,其中單層SMA的體積分數為50%,通過該模塊的Analysis功能分析可得SMA/石墨/環氧樹脂單層板的材料參數,各材料參數定義同石墨/環氧樹脂材料,材料參數如表3所示。

表3 SMA/石墨/環氧樹脂單層板的材料參數
2.3 鋪層方案確定
對2種剛度配置方式分別鋪層,復合材料薄壁梁的上下左右壁都鋪設6層,中間層鋪設12層。鋪層角為45°,鋪層單層厚度t=0.127 mm。
2.4 模態分析
ACP模塊進行SMA混雜復合材料箱型薄壁梁模態分析的工作流程如圖4所示。

圖4 SMA混雜復合材料箱型薄壁梁模態分析的工作流程
選取模態分析時指定6階載荷步選項,復合材料懸臂梁的一端固定,一端自由,模態提取方法采用Damped法,這是因為考慮SMA的非線性特性,同時輸入SMA的等效剛度及阻尼比進行求解。
2.5 結果后處理
在MODEL模塊獲取復合材料懸臂梁的固有頻率和振型,并對其進行分析。
3 ANSYS有限元結果分析及討論
3.1 振型分析
以鋪層角為45°的CUS構型為例,SMA混雜復合材料箱型薄壁梁的前6階振型如圖5~圖10所示。從圖5~圖10可以看出,CUS構型下,第一階振型以揮舞振動為主;第二階振型以擺振為主;第三階、第四階及第五階以彎曲為主,第六階以扭轉為主。CAS構型的前6階振型和CUS的相似。

圖5 一階模態振型
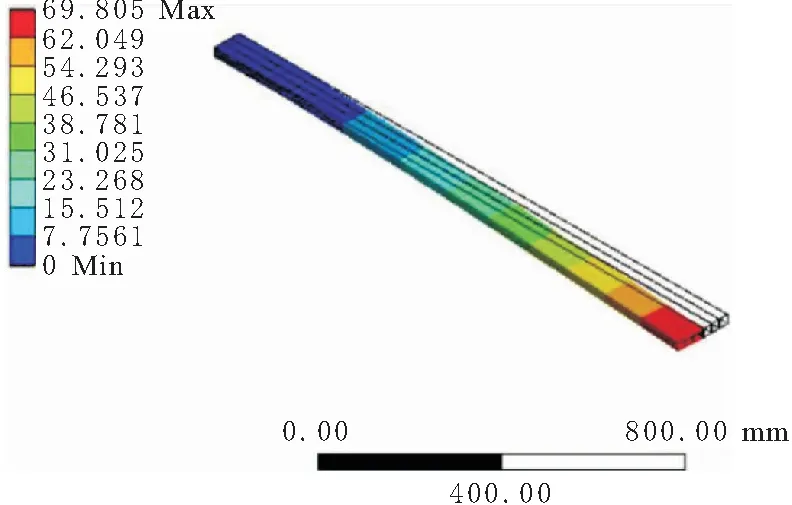
圖6 二階模態

圖7 三階模態振型

圖8 四階模態振型

圖9 五階模態振型

圖10 六階模態振型
3.2 固有頻率分析
3.2.1 有無SMA的影響
表4和表5分別為不含SMA和含SMA的復合材料懸臂梁在CUS構型下的前5階固有頻率,同時考慮了鋪層角度的影響。

表4 不含SMA混雜復合材料箱型薄壁梁懸臂梁的前5階固有頻率

表5 含SMA混雜復合材料箱型薄壁梁懸臂梁的前5階固有頻率
由表4和表5可以看出,復合材料箱型薄壁梁前5階各階的固有頻率隨著鋪設角度的增加而減小;同一鋪設角度下,復合材料箱型薄壁梁的固有頻率隨著階數的增加而逐漸增大。加入SMA纖維之后,相對于不含SMA的復合材料箱型薄壁梁的前5階固有頻率減小,且鋪設角為0°時,固有頻率降幅最大,以鋪設角為0°的二階頻率為例,相對于不含SMA的混雜復合材料箱型薄壁梁的固有頻率降低了28.21%。
3.2.2 不同的配置方式
表6和表7分別為CUS和CAS 2種構型下SMA混雜復合材料箱型薄壁梁的前5階固有頻率,其中考慮了鋪層角度的影響。

表6 CUS構型下SMA混雜復合材料箱型薄壁梁的前5階固有頻率

表7 CAS構型下SMA混雜復合材料箱型薄壁梁的前5階固有頻率
從表6和表7可以看出,2種構型下的前5階固有頻率隨著鋪層角度的增加而減小,但減小的幅度越來越小。同一鋪設角度下,隨著階數的增大而增大。以2種構型下的一階頻率和二階頻率進行比較,比較的結果分別如圖11和圖12所示。

圖11 一階固有頻率

圖12 二階固有頻率
從圖11和圖12可以看出,2種構型下的一階固有頻率隨鋪設角度的變化曲線走勢一致,基本吻合,說明不同的配置方式對一階和二階的固有頻率影響不大。接下來的分析主要針對CUS構型進行分析。
3.2.3 寬高比的影響
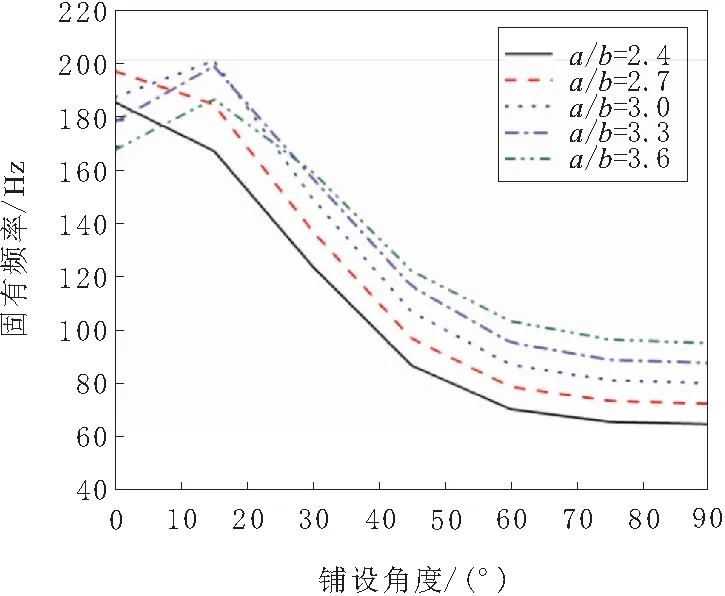
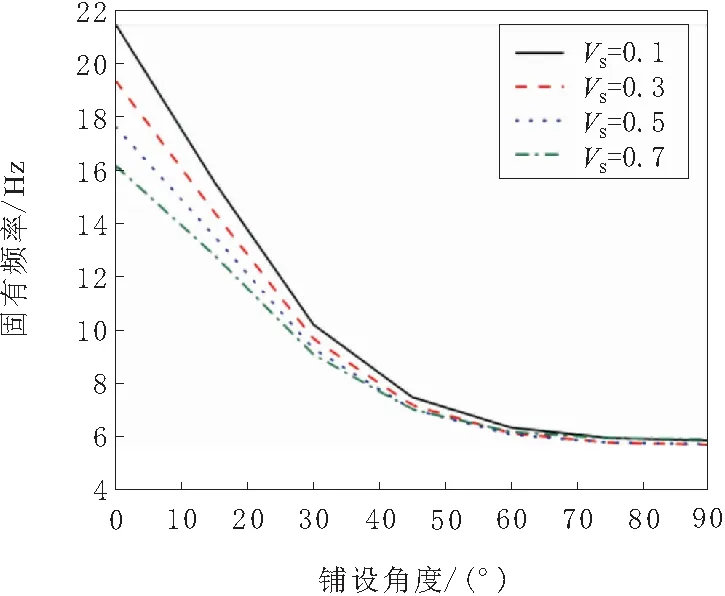
以CUS構型前4階固有頻率為例,保持b=0.025 m,寬高比(a/b)分別取2.4,2.7,3.0,3.3,3.6時,SMA混雜復合材料懸臂梁在不同寬高比下的前4階固有頻率如圖13~圖16所示,同時也顯示出鋪層角度的影響。
由圖13~圖16可以看出,CUS構型下前4階固有頻率隨著寬高比的增大而增大,其中二階和四階固有頻率隨著寬高比的增大增幅明顯,一階和三階固有頻率增幅不大,說明增加橫截面寬高比可以在一定程度上增加箱型梁的阻尼,使復合材料箱型懸臂梁的固有頻率降低。在同一寬高比下,前4階固有頻率隨著鋪設角度的增加而逐漸減小。由圖16可以看出,當2.4 圖13 一階固有頻率 圖14 二階固有頻率 圖15 三階固有頻率 圖16 四階固有頻率 3.2.4 不同單層SMA體積含量的影響 圖17~圖20給出了復合材料懸臂梁每一SMA/石墨/環氧樹脂單層中,SMA體積含量分別為10%、30%、50%和70%時,復合材料懸臂梁的前4階固有頻率隨鋪設角度的變化曲線。 圖17 一階固有頻率 圖18 二階固有頻率 圖19 三階固有頻率 圖20 四階固有頻率 由圖17~圖20可以看出,隨著單層SMA體積含量的增加,前4階的固有頻率隨著鋪設角度的增加而逐漸減小。這是因為SMA的彈性模量小于石墨/環氧樹脂材料的彈性模量,SMA體積含量越大增大,使得SMA/石墨/環氧樹脂單層板的EX就越小,導致SMA混雜復合材料懸臂梁的固有頻率降低。 3.2.5 SMA不同的安裝位置 保持SMA/石墨/環氧樹脂單層板中SMA體積含量不變,單層SMA的體積含量為50%,改變SMA/石墨/環氧樹脂單層板的安裝位置,來分析SMA不同的安裝位置對混雜復合材料箱型薄壁梁固有頻率的影響。安裝位置1,復合材料懸臂梁的頂層;位置2,復合材料懸臂梁的中性層;位置3,復合材料懸臂梁的底層。 圖21~圖24給出了復合材料懸臂梁在不同的安裝位置下前4階固有頻率隨鋪設角度的變化曲線。 由圖21~圖24可以看出,SMA在不同安裝位置下復合材料懸臂梁前4階固有頻率隨鋪設角的變化曲線走勢一致,基本吻合。說明SMA不同的安裝位置對復合材料懸臂梁的固有頻率的影響不大。 圖21 一階固有頻率 圖22 二階固有頻率 圖23 三階固有頻率 圖24 四階固有頻率 采用ANSYS軟件對SMA混雜復合材料箱型薄壁懸臂梁進行模態分析,得出以下結論。 a.與不含SMA混雜復合材料箱型薄壁懸臂梁相比較,加入SMA纖維后,復合材料箱型薄壁梁的剛度降低,固有頻率隨之降低。 b.在CUS和CAS 2種配置方式下,SMA混雜復合材料箱型薄壁懸臂梁的固有頻率隨鋪設角度的變化曲線走勢一致,基本吻合,說明這2種配置方式對SMA混雜復合材料箱型薄壁懸臂梁的固有頻率影響不大。 c.SMA混雜復合材料箱型薄壁懸臂梁的固有頻率隨著寬高比的增大而增大,其中,二階和四階固有頻率增幅明顯。 d.SMA纖維鋪設角對復合材料箱型薄壁懸臂梁的固有頻率能夠產生顯著的影響。在鋪設角度0~45°范圍內,隨著鋪設角度的增加,復合材料懸臂梁的各階固有頻率降低明顯;當鋪設角度在45~90°范圍內,隨著鋪設角度的增加,固有頻率降低逐漸平緩。 e.SMA混雜復合材料箱型薄壁梁的固有頻率隨著單層SMA的體積含量的增加而逐漸降低。其中,在鋪設角0~45°范圍內固有頻率影響較大。 f.SMA纖維3種不同的安裝位置對復合材料箱型懸臂梁的固有頻率影響較小。同一鋪設角度下,復合材料箱型薄壁梁在SMA纖維3種不同安裝位置下的固有頻率基本相同。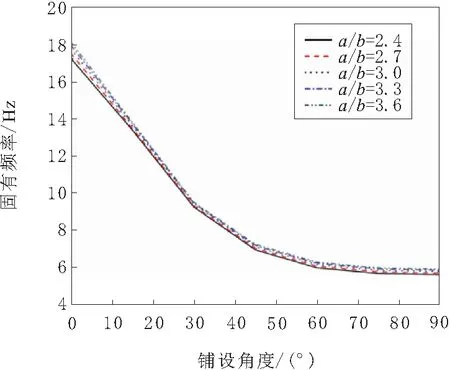









4 結束語

